Archive
Agile and Waterfall as community norms
While rapidly evolving computer hardware has been a topic of frequent public discussion since the first electronic computer, it has taken over 40 years for the issue of rapidly evolving customer requirements to become a frequent topic of public discussion (thanks to the Internet).
The following quote is from the Opening Address, by Andrew Booth, of the 1959 Working Conference on Automatic Programming of Digital Computers (published as the first “Annual Review in Automatic Programming”):
'Users do not know what they wish to do.' This is a profound truth. Anyone who has had the running of a computing machine, and, especially, the running of such a machine when machines were rare and computing time was of extreme value, will know, with exasperation, of the user who presents a likely problem and who, after a considerable time both of machine and of programmer, is presented with an answer. He then either has lost interest in the problem altogether, or alternatively has decided that he wants something else. |
Why did the issue of evolving customer requirements lurk in the shadows for so long?
Some of the reasons include:
- established production techniques were applied to the process of building software systems. What is now known in software circles as the Waterfall model was/is an established technique. The figure below is from the 1956 paper Production of Large Computer Programs by Herbert Benington (Winston Royce’s 1970 paper has become known as the paper that introduced Waterfall, but the contents actually propose adding iterations to what Royce treats as an established process):
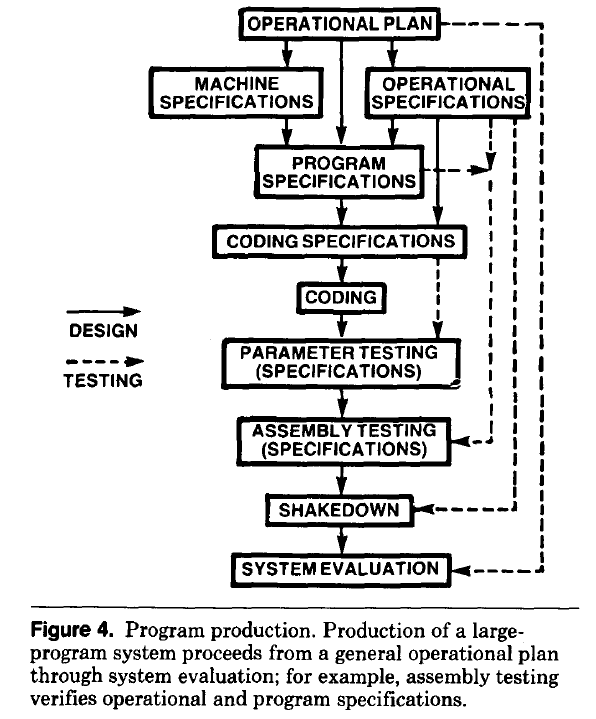
- management do not appreciate how quickly requirements can change (at least until they have experience of application development). In the 1980s, when microcomputers were first being adopted by businesses, I had many conversations with domain experts who were novice programmers building their first application for their business/customers. They were invariably surprised by the rate at which requirements changed, as development progressed.
While in public the issue lurked in the shadows, my experience is that projects claiming to be using Waterfall invariably had back-channel iterations, and requirements were traded, i.e., drop those and add these. Pre-Internet, any schedule involving more than two releases a year could be claimed to be making frequent releases.
Managers claimed to be using Waterfall because it was what everybody else did (yes, some used it because it was the most effective technique for their situation, and on some new projects it may still be the most effective technique).
Now that the issue of rapidly evolving requirements is out of the closet, what’s to stop Agile, in some form, being widely used when ‘rapidly evolving’ needs to be handled?
Discussion around Agile focuses on customers and developers, with middle management not getting much of a look-in. Companies using Agile don’t have many layers of management. Switching to Agile results in a lot of power shifting from middle management to development teams, in fact, these middle managers now look surplus to requirements. No manager is going to support switching to a development approach that makes them redundant.
Adam Yuret has another theory for why Agile won’t spread within enterprises. Making developers the arbiters of maximizing customer value prevents executives mandating new product features that further their own agenda, e.g., adding features that their boss likes, but have little customer demand.
The management incentives against using Agile in practice does not prevent claims being made about using Agile.
Now that Agile is what everybody claims to be using, managers who don’t want to stand out from the crowd find a way of being part of the community.
How did Agile become the product development zeitgeist?
From the earliest days of computing, people/groups have proposed software development techniques, and claiming them to be effective/productive ways of building software systems. Agile escaped this well of widely unknowns to become the dominant umbrella term for a variety of widely used software development methodologies (I’m talking about the term Agile, not any of the multitude of techniques claiming to be the true Agile way). How did this happen?
The Agile Manifesto was published in 2001, just as commercial use of the Internet was going through its exponential growth phase.
During the creation of a new market, as the Internet then was, there are no established companies filling the various product niches; being first to market provides an opportunity for a company to capture and maintain a dominate market share. Having a minimal viable product, for customers to use today, is critical.
In a fast-growing market, product functionality is likely to be fluid until good enough practices are figure out, i.e., there is a lack of established products whose functionality new entrants need to match or exceed.
The Agile Manifesto’s principles of early, continuous delivery, and welcoming of changing requirements are great strategic advice for building products in a new fast-growing market.
Now, I’m not saying that the early Internet based companies were following a heavy process driven approach, discovered Agile and switched to this new technique. No.
I’m claiming that the early Internet based companies were releasing whatever they had, with a few attracting enough customers to fund further product development. Based on customer feedback, or not, support was added for what were thought to be useful new features. If the new features kept/attracted customers, the evolution of the product could continue. Did these companies describe their development process as throw it at the wall and see what sticks? Claiming to be following sound practices, such as doing Agile, enables a company to appear to be in control of what they are doing.
The Internet did more than just provide a new market, it also provided a mechanism for near instantaneous zero cost product updates. The time/cost of burning thousands of CDs and shipping them to customers made continuous updates unrealistic, pre-Internet. Low volume shipments used to be made to important customers (when developing a code generator for a new computer, I sometimes used to receive OS updates on a tape, via the post-office).
The Agile zeitgeist comes from its association with many, mostly Internet related, successful software projects.
While an Agile process works well in some environments (e.g., when the development company can decide to update the software, because they run the servers), it can be problematic in others.
Agile processes are dependent on customer feedback, and making updates available via the Internet does not guarantee that customers will always install the latest version. Building software systems under contract, using an Agile process, only stands a chance of reaping any benefits when the customer is a partner in the same process, e.g., not using a Waterfall approach like the customer did in the Surrey police SIREN project.
Agile was in the right place at the right time.
Median system cpu clock frequency over last 15 years
We are all familiar with graphs showing the growth of cpu clock frequency over time. The data for these plots is based on vendor announcements listing the characteristics of their latest products, and invariably focuses on the product which is the fastest or contains the most transistors or the lowest power consumption.
Some customers buy the cpu with the highest/most/lowest, but many are happy to pay less for, for good enough. What does a graph of average customer cpu clock frequency over time look like?
Vendors sometimes publish general sales figures, but I have never seen one broken down by clock frequency. However, a few sites collect user system data, including:
- A subset of the Linux Counter project data is available. This does not contain explicit date information, but a must-be-later-than date can be inferred from the listed Linux kernel version,
- Hardware for BSD has data going back to December 2014, but there is no obvious way to extract it (I have not tried that hard),
- the BSDstats project (variable website availability) has been collecting data on machines running some derivative of BSD since August 2008; it contains around 200 times more cpu data than the known Linux Counter data. While the raw data is not available, approximately monthly reports are available on the Wayback Machine.
A BSDstats cpu history was obtained using waybackpack to download the available stored cpu summary pages, followed by html2text, and an awk script to extract the cpu frequency/count data.
BSDstats obtains the cpu information via a call to the sysctl command. For many Intel processors, but not AMD processors, the returned string includes the frequency (to see your cpu information on Linux systems type: more /proc/cpu), for instance:
Celeron(R) CPU 2.80GHz | 336 Pentium(R) 4 CPU 3.00GHz | 258 Pentium(R) 4 CPU 2.40GHz | 170 Athlon(tm) 64 Processor 3000+ | 43 Athlon(tm) 64 X2 Dual Core Processor 4200+ | 28 Athlon(tm) 64 Processor 3500+ | 27 |
For simplicity, only those rows containing frequency information were used in this analysis; 67% of the strings explicitly included a frequency (this saved me having to build a table to map AMD cpu strings to their corresponding frequency).
The plot below shows median cpu frequency (in red), along with the top/bottom 10% cpu frequencies, based on the Wayback Machine’s copy of the webpage on a given date, for a total of 2,304,446 cpu identities (code+data):
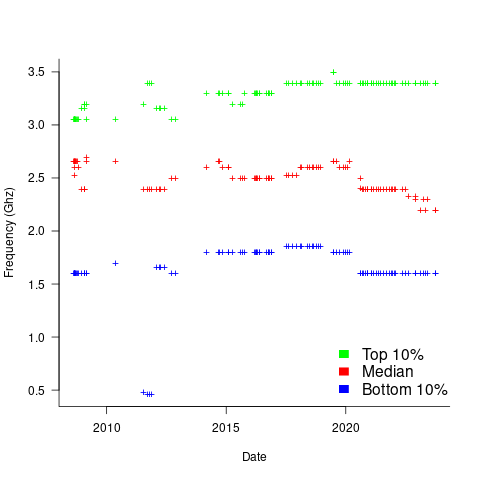
Broadly, the plot shows that cpu frequencies have essentially remained unchanged since 2008, with systems running BSD having a median frequency of 2.5 GHz, with 10% of systems having a frequency over 3.5 GHz, and 10% of systems a frequency below 1.5 GHz.
I was surprised at how many different frequencies were present in the data; often over 50. A look at the large number of different versions of Intel x86 cpus suggests that this is to be expected.
How representative is this sample of BSD systems, compared to the many more systems running Linux and Windows?
This begs the question of what kinds of environments are being compared. Are these desktop systems, local or hosted clusters, cloud systems?
The plot below shows the total number of cpus summarised on each Wayback Machine snapshot (code+data):

A few thousand systems are likely to be personal desktop systems, while the tens of thousands are likely to be clusters or small cloud providers.
Pointers to more data, particularly pre-2000, most welcome.
Documentation as a signal of program size
Developers and researchers invariably measure program size in lines of code, while senior managers measure by resources consumed per accounting period, e.g., money and people.
What size signals are visible to the users of a program?
Before CDs became generally available at the start of the 1990s, software for desktop computers was delivered on floppy discs that did not have the capacity to hold documentation (i.e., 128K to 1.4M), which was distributed in printed book form.
For instance, the first version of Turbo Pascal came with one 5¼ floppy (the compiler+IDE occupied 28K) and a 276-page reference manual.
Today, people are familiar with the intangible nature of software. In previous ages, people wanted to see and feel something for their money, and printed manuals were the substance they received (some products attached the floppies inside the back covers). Physical manuals were also thought to reduce software piracy (when CDs arrived, there was lots of hand-wringing over including electronic manuals).
Microsoft Windows bucked the trend, distributed with almost no physical paper, but many floppies; 13 3½ floppies for the initial upgrade to Windows 95, and 26 for Service Release 2 (oh, the fun of spending an afternoon swapping disks to rebuild a machine). Microsoft Office 97 standard edition was available on 45 floppies, the professional edition on 55.
The problem with distributing manuals in printed book form is that updates are costly; customers need a whole new book and the existing inventory needs to be scrapped. Documentation for Mainframe/Minicomputer/Workstations came in ring binders, allowing updates on an individual page basis. The Sun 4 that arrived at my office (to have a COBOL code generator written for the SPARC cpu) came with around 3-feet of ring binders. I have seen offices with a wall of shelves filled with vendor ring binders.
Is there any correlation between a project’s lines of code and pages of it’s documentation?
Most developers hate writing documentation; readmes don’t count. This means that only (well) funded development projects are likely to pay for an author to produce some amount of non-trivial documentation (a widely used application eventually attracts an external author interested in explaining things). Some Open source projects do contain files believed to be documentation; documentation research is primarily focused on accuracy (see section 6.4.4).
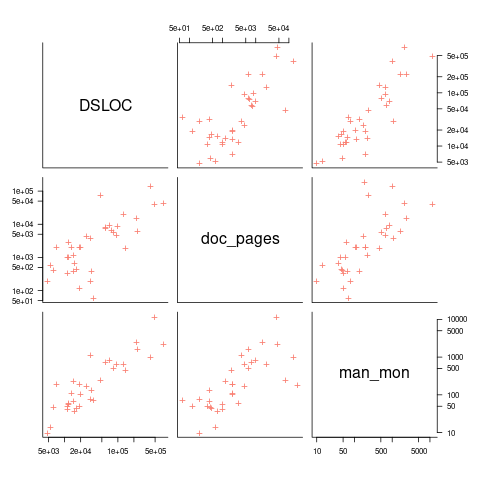
The only data I am aware of containing LOC, documentation page counts, and development man months is the 1979 paper The Characteristics of Large Systems by Belady and Lehman, which lists values for 37 “… independent programs developed in a large software house.” How much of the documentation was user focused, requirements+business logic, or developer focused? I have no idea (a fitted regression model, code+data, shows an almost linear relationship between LOC and document pages). Tests are not broken out as a separate item (code, documentation, not recorded?)
The plot below shows delivered: source lines of code, documentation pages, and total man months, x/y-axis both using log scales (code+data):
The total man months of implementation for each project is taken up by writing the code and documentation. The following equation is a good fit (explaining just 80% of the variance; code+data): 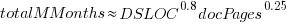 , but is only slightly better than
, but is only slightly better than 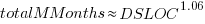 . Given the high correlation between
. Given the high correlation between 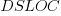 and
and 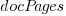 , including both in the same model is probably not a good idea (the equation:
, including both in the same model is probably not a good idea (the equation: 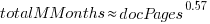 explains just over 50% of the variance).
explains just over 50% of the variance).
There are a few possible outliers in the data. Perhaps removing these would make the picture clearer.
For me, what stands out, compared to today’s projects, is the relatively low DSLOC (a few tens of thousands) and high pages of documentation (thousands). Projects could be smaller/simpler in the 1970s because they were often replacing humans doing the work, not previously written systems; or, perhaps projects were limited by available computer memory, often well less than a megabyte. Perhaps I think the page count is high because I don’t have an accurate idea of how much online documentation is created these days.
My 2023 in software engineering
In a 2009 post, I predicted that Chinese and Indian developers would become a major influence in the next decade. This year, it was very noticeable that many of the authors of papers at major conferences had Asian names. I would say that, on average, papers with Asian author names were better than papers by authors with non-Asian names.
While LLMs dominated the software news this year, the lead time for research projects and conference submission deadlines meant that few of the papers accepted at this year’s top ranked conferences were LLM based, e.g., around 5% at ICSE. I expect there will be a much higher percentage of LLM based papers in 2024, which I think will be a disaster for software engineering research, at least in the short term. From what I have seen and read, much of LLM based software engineering is driven by fashion and/or a desire to gain experience that leads to a job in AI. Discovering something useful about software development takes a back seat (the current fashionable topic, butterfly collecting, at least produces potentially useful datasets). I think that LLMs are going to be very useful for analyzing text data, e.g., named entity recognition.
London based, software related meetups have come back to life. I go to around 1-2 a week, and the regular good ones include: Internet of Things, Extreme Tuesday Club, London Prompt Engineers, and London R. On the academic front, I have started attending the software reliability seminars at Imperial, and funding means that the excellent Crest Open Workshops are down to two a year. There were a handful of hackathons this year, and I got to go to one of them, a LLM hackathon.
Not usually software specific: Newspeak House hosts a variety of events that are often attended by many developers and those associated with the rationalist community. I attend maybe 2–3 events a month.
What did I learn/discover about software engineering this year?
- A small team estimation dataset showed the same kinds of patterns seen in larger teams,
- more cost/benefit analysis of software engineering activities here and here,
- data on Cobol source is very rare, and I found some,
- programs often continue to work very well in the presence of serious coding mistakes; I discovered some conditions where this occurs (to be continued next year),
- yet more debunking of software folklore: Optimal function length, and Hardware/Software cost ratio,
- I fell down the rabbit hole of early computer performance and their benchmarks.
The evidence-based software engineering Discord channel ticks over (invitation), with sporadic interesting exchanges.
Sample size needed to compare performance of two languages
A humungous organization wants to minimise one or more of: program development time/cost, coding mistakes made, maintenance time/cost, and have decided to use either of the existing languages X or Y.
To make an informed decision, it is necessary to collect the required data on time/cost/mistakes by monitoring the development process, and recording the appropriate information.
The variability of developer performance, and language/problem interaction means that it is necessary to monitor multiple development teams and multiple language/problem pairs, using statistical techniques to detect any language driven implementation performance differences.
How many development teams need to be monitored to reliably detect a performance difference driven by language used, given the variability of the major factors involved in the process?
If we assume that implementation times, for the same program, have a normal distribution (it might lean towards lognormal, but the maths is horrible), then there is a known formula. Three values need to be specified, and plug into this formula: the statistical significance (i.e., the probability of detecting an effect when none is present, say 5%), the statistical power (i.e., the probability of detecting that an effect is present, say 80%), and Cohen’s d; for an overview see section 10.2.
Cohen’s d is the ratio 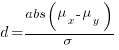 , where
, where 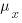 and
and 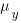 is the mean value of the quantity being measured for the programs written in the respective languages, and
is the mean value of the quantity being measured for the programs written in the respective languages, and 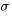 is the pooled standard deviation.
is the pooled standard deviation.
Say the mean time to implement a program is 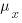 , what is a good estimate for the pooled standard deviation,
, what is a good estimate for the pooled standard deviation, 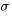 , of the implementation times?
, of the implementation times?
Having 66% of teams delivering within a factor of two of the mean delivery time is consistent with variation in LOC for the same program and estimation accuracy, and if anything sound slow (to me).
Rewriting the Cohen’s d ratio: 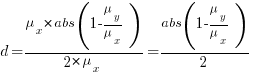
If the implementation time when using language X is half that of using Y, we get 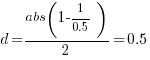 . Plugging the three values into the
. Plugging the three values into the pwr.t.test function, in R’s pwr package, we get:
> library("pwr")
> pwr.t.test(d=0.5, sig.level=0.05, power=0.8)
Two-sample t test power calculation
n = 63.76561
d = 0.5
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group |
In other words, data from 64 teams using language X and 64 teams using language Y is needed to reliably detect (at the chosen level of significance and power) whether there is a difference in the mean performance (of whatever was measured) when implementing the same project.
The plot below shows sample size required for a t-test testing for a difference between two means, for a range of X/Y mean performance ratios, with red line showing the commonly used values (listed above) and other colors showing sample sizes for more relaxed acceptance bounds (code):
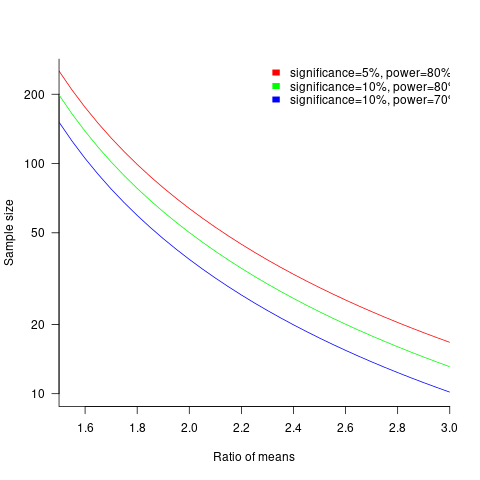
Unless the performance difference between languages is very large (e.g., a factor of three) the required sample size is going to push measurement costs into many tens of millions (£1 million per team, to develop a realistic application, multiplied by two and then multiplied by sample size).
For small programs solving certain kinds of problems, a factor of three, or more, performance difference between languages is not unusual (e.g., me using R for this post, versus using Python). As programs grow, the mundane code becomes more and more dominant, with the special case language performance gains playing an outsized role in story telling.
There have been studies comparing pairs of languages. Unfortunately, most have involved students implementing short problems, one attempted to measure the impact of programming language on coding competition performance (and gets very confused), the largest study I know of compared Fortran and Ada implementations of a satellite ground station support system.
The performance difference detected may be due to the particular problem implemented. The language/problem performance correlation can be solved by implementing a wide range of problems (using 64 teams per language).
A statistically meaningful comparison of the implementation costs of language pairs will take many years and cost many millions. This question is unlikely to every be answered. Move on.
My view is that, at least for the widely used languages, the implementation/maintenance performance issues are primarily driven by the ecosystem, rather than the language.
Patches for the code of Peter Turchin’s Attrition Warfare Model
The paper Empirically Testing Predictions of an Attrition on Warfare Model for the War in Ukraine, by Peter Turchin, recently showed up during one of my regular searches for software engineering data. A quick scan of the paper founded that it is very empirical, and that the analysis coding was done in R; I could not resist checking out the source code.
One of my first jobs was helping academics fix coding issues with the programs they had written to solve scientific/engineering problems, and this R code reminded me of several habits of scientists who code: the single letter variables used in equations are directly mapped to identifier names, and there is no structure to the code. The code is so short (86 lines) that the lack of structure is a minor inconvenience; a few thousand lines, and it becomes a major headache. The code for Imperial’s COVID model was ten times larger.
Two mistakes in the code/paper jumped out at me, leading to this post. First, some background.
The empirical predictions in the paper are intended to provide insight into who is likely to win the ongoing Ukraine/Russia war. Fighting requires soldiers and these are killed/wounded over time. The country that does not have enough soldiers to at least keep the opposition at bay, looses.
Turchin has proposed what he calls the Attrition War model, based on Lanchester’s laws (various attempts to validate Lanchester’s models, lots of maths to shake a stick at), and the paper solves this model’s set of eight differential equations (each country has the same set of four equations; the connection between the two sets is that one country’s casualty rate and Army size is influenced by the opposing country’s stock of war matériel). The four quantities modelled are casualties, army size, stock of warfare matériel, and production capacity.
Getting predictions out of differential equations requires being able to find a solution to the equations and feeding in numeric values for the various parameters.
Solving the equations is a maths problem, i.e., no knowledge of military matters required. Selecting the equations to solve and the numeric values to feed into the solution is what requires military knowledge. I don’t know anything about military matters; the following analysis is purely related to writing code to solve a set of differential equations, using the equations plus numeric values in Turchin’s November 2023 paper.
For obvious reasons, countries involved in the war do not publish information on the quantities modelled by these equations (which are also likely to be time-dependent). Turchin addresses the changeable nature of the numeric values by introducing various random components into his Attrition model.
From the perspective of solving the eight equations and presenting the results, the following are the two mistakes that jumped out at me (both involving the implementation of the random component):
- When a model contains a random component, there will be a huge/infinite number of possible solutions. The takeaway plots in the paper show a single solution (for each of the four variables/two countries), with the width of the plotted lines and their fluctuating appearance suggesting that they contain multiple solutions. The plot below left shows the solution for artillery shell production over time, as it appears in the paper, while the plot below right shows 100 solutions (each line is a different solution; code):
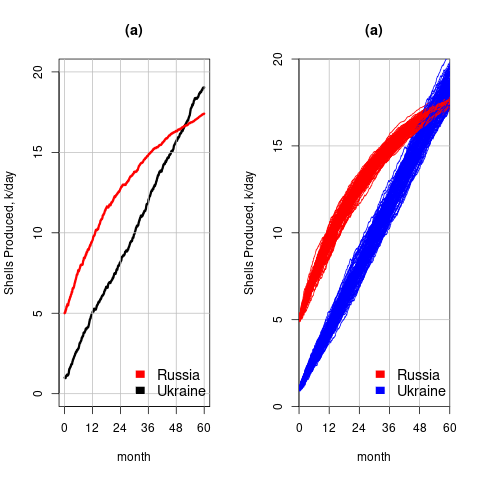
The wedge of lines shows the range of possible solutions (each line drawn overwrites anything previously drawn, and plotting with transparent colors would show the density of solution at a given point; I decided to keep the code simple).
- All the random components are assumed to have a Gaussian distribution. When distribution information is not available, this is usually a safe choice. However, two of the random components must always have non-negative values (i.e., casualties and matériel used can never be negative). The Poisson distribution is the obvious candidate, and a simple search turned up an empirical paper agreeing with this choice (at least for casualties).
The plot below left shows one solution for the number of casualties over time, using the original code, while the plot below right shows 100 solutions using a Poisson distribution for the random component (code):
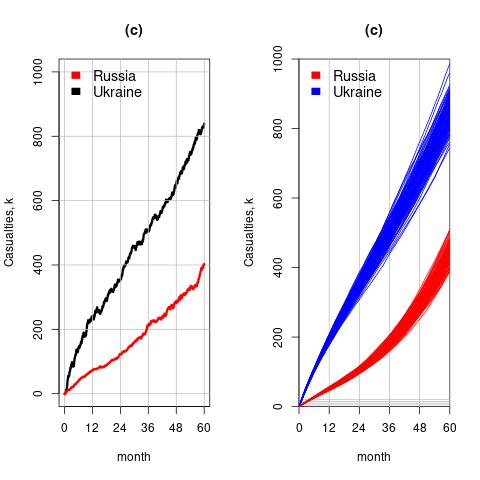
With a Poisson random component, the solutions don’t meander as much, and the variance is smaller than when a Gaussian is used. Technically, it is a more accurate model (if more variance is to be expected a Negative Binomial distribution could be used; see commented out code)
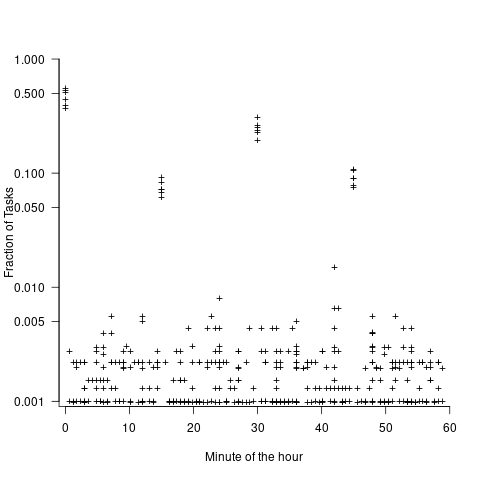
The latest (November) UK government estimate of Russian casualties is 300K, roughly three times larger than predicted by Turchin’s model. Changing the value for the ‘conversion rate of expended matériel to casualties’ from
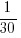 to
to 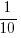 brings the casualty prediction inline with current estimates (we have been hearing a lot about the accuracy of the Ukrainian targetting; see code for details).
brings the casualty prediction inline with current estimates (we have been hearing a lot about the accuracy of the Ukrainian targetting; see code for details).
I have also reworked the code to add some structure, e.g., separating out solving the equations and setting the initial conditions.
Turchin used the traditional approach to solving differential equations, the one we are taught at school. Before seeing the code, I was half expecting to see a System dynamics approach. The advantage of a systems dynamic approach is flexibility (i.e., easier to add more components) and visualization (i.e., a chart showing what feeds into/out of what); an example. There is an R-based book: System Dynamics Modelling with R.
Christmas books for 2023
This year’s Christmas book list, based on what I read this year, and for the first time including a blog series that I’m sure will eventually appear in book form.
“To Explain the World: The discovery of modern science” by Steven Weinberg, 2015. Unless you know that Steven Weinberg won a physics Nobel prize, this looks like just another history of science book (the preface tells us that he also taught a history of science course for over a decade). This book is written by a scientist who appears to have read the original material (I’m assuming in translation), who puts the discoveries and the scientists involved at the center of the discussion; this is not the usual historian who sprinkles in a bit about science, while discussing the cast of period characters. For instance, I had never understood why the work of Galileo was considered to be so important (almost as a footnote, historians list a few discoveries of his). Weinberg devotes pages to discussing Galileo’s many discoveries (his mathematics was a big behind the times, continuing to use a geometric approach, rather than the newer algebraic techniques), and I now have a good appreciation of why Galileo is rated so highly by scientists down the ages.
Chapter 2 of “When Old Technologies Were New: Thinking about electric communication in the late nineteenth century” by Carolyn Marvin, 1988. The book is worth buying just for chapter 2, which contains many hilarious examples of how the newly introduced telephone threw a spanner in to the workings of the social etiquette of the class of person who could afford to install one. Suitors could talk to daughters without other family members being present, public phone booths allowed any class of person to be connected directly to the man of the house, and when phone companies started publishing publicly available directories containing subscriber name/address/number, WELL!?! In the US there were 1 million telephones installed by 1899, and subscribers were sometimes able to listen to live musical concerts and sports events (commercial radio broadcasting did not start until the 1920s).
“The Grand Strategy of the Roman Empire: From the first century A.D. to the third” by Edward Luttwak, 1976; h/t Mr. and Mrs. Psmith’s review. I cannot improve or add to John Psmith’s review. The book contains more details; the review captures the essence. On a related note, for the hard core data scientists out there: Early Imperial Roman army campaigning: observations on marching metrics, energy expenditure and the building of marching camps.
“Innovation and Market Structure: Lessons from the computer and semiconductor industries” by Nancy S. Dorfman, 1987. An economic perspective on the business of making and selling computers, from the mid-1940s to the mid-1980s. Lots of insights, (some) data, and specific examples (for the most part, the historians of computing are, well, historians who can craft a good narrative, but the insights are often lacking). The references led me to: Mancke, Fisher, and McKie, who condensed the 100K+ pages of trial transcript from the 1969–1982 IBM antitrust trial down to 1,500+ pages of Historical narrative.
Worshipping the Future by Helen Dale and Lorenzo Warby. Is “… a series of essays dissecting the social mechanisms that have led to the strange and disorienting times in which we live.” The series is a well written analysis that attempts to “… understand mechanisms of how and the why, …” of Woke.
Honourable mentions
“The Big Con: The story of the confidence man and the confidence trick” by David W. Maurer (source material for the film The Sting).
“Cubed: A secret history of the workplace” by Nikil Saval.
Software engineering’s F word
I know of two conversation topics that are guaranteed to make software developers feel uncomfortable, and even walk away: 1) complaining about ChatGPT’s refusable to say anything nice about Adolf Hitler, 2) enquiring why so few people are willing to talk about software engineering’s three letter F word (I actually say the F word).
Academics don’t like to use the F word, preferring phrases such as recreational value (and then only for Open source; earlier this year, I used hedonistic activity in the title of a blog post). A 2012 review of motivation in open source development found 10, out of 40, papers listing the F word as a motivator (all published in management related venues).
The F word occurs in the title of a 1991 article in the newsletter The Software Practitioner, aimed at professional developers: “Torn Between Fun and Tedium” by Bruce Blum. The article appears to be lost, but is discussed in the book software creativity 2.0 by Robert Glass.
Blum assumes that software development work is either Fun or Tedium, and assigns a Fun/Tedium percentage to various phase of a Waterfall software lifecycle.
Selling the project concept is assigned 100/0 by Blum, (i.e., 100% Fun; me: 80/20), developing the requirements is 50/50 (me: 20/80), top level design is 40/60 (me: 80/20), detailed design 33/67 (me: no idea), programming 75/25 (me: agree), testing 33/67 (me: 75/25), and maintenance 0/100 (me: 25/75).
I regularly have younger developers tell me that they picked a particular new technology because it looked like fun to learn and use; older developers have been through this phase new technology phase, and sometimes other phases, and have moved onto being more interested in avoiding grief.
Where is the evidence for this fun seeking? Asking developers about fun in their software engineering day job is not socially acceptable, but it is ok to ask about fun in personal projects.
I suspect that managers who have had little contact with working developers would be shocked by the extent to which fun motivates developer decisions; managers who have had to deal with the practicalities of herding developers less so.
Rounding in reported task implementation time
There is lots of evidence that people often pick a round number when estimating the time needed to implement a task. Parkinson’s law suggests that reported actual implementation time will often also be a round number, e.g., report 30 minutes for a task that actually took 28 minutes.
If a task is estimated to take 1-hour, what is the distribution of reported implementations times? The analysis in this article uses the SiP task dataset, and similar patterns occur in other datasets.
The plot below shows the number of tasks having a given reported implementation time, for tasks estimated to take 1-hour, with main peaks labelled in red (reported times rounded to one decimal place and quarter hours; code+data):
With 1-hour estimates, there is limited scope for a wide range of actual times (at least for times less than estimates). The labelled peaks contain 89% of 1-hour estimate tasks (1,525 tasks, 21% less than estimate, 44% equal estimate, 24% greater than estimate).
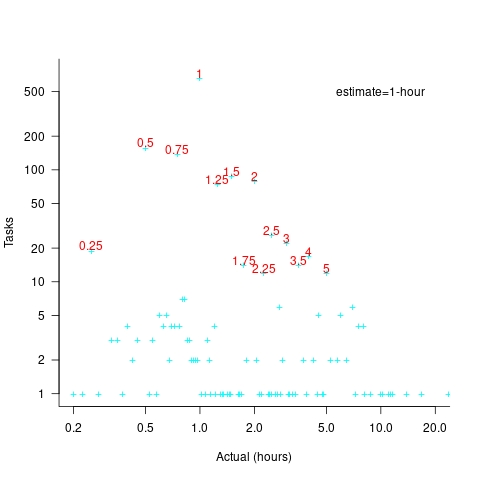
Tasks with larger estimated times are likely to take longer, creating more possible rounding peaks in the implementation time distribution. The plot below shows the number of tasks having a given reported implementation time, for tasks estimated to take 7-hour (i.e., 1-day), with main peaks labelled in red (reported times rounded to one decimal place and quarter hours; code+data):
As expected, there are more peaks and implementation times are distributed over a larger range of values.
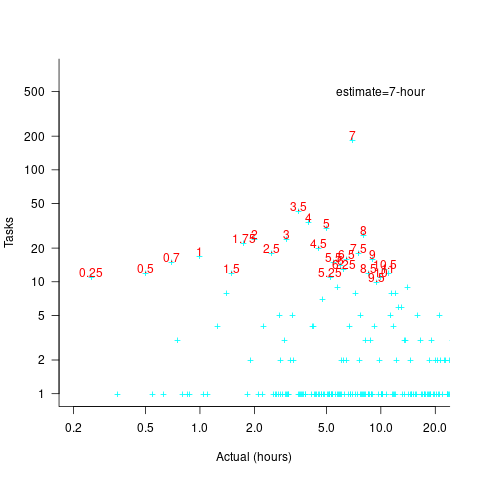
These plots suggest that many actual times are being rounded to 15-minute intervals. The plot below is based on the minute portion of the reported time (i.e., the hour part is ignored), and shows the fraction of tasks, for estimates of 1, 2, 3, 5, 7, and 14 hours, whose minute component of reported time has a given value (code+data):
For estimates of a few hours, around 90% of reported task time is on a 15-minute mark, while for 7- and 14-hour tasks the percentage drops to 80%.
If staff are manually entering task finish times, then some degree of rounding is to be expected. When the finish time is indirectly calculated, based on the submission of a completed form, there will be some fuzziness to the rounding number process.
Recent Comments