Archive
Sample size needed to compare performance of two languages
A humungous organization wants to minimise one or more of: program development time/cost, coding mistakes made, maintenance time/cost, and have decided to use either of the existing languages X or Y.
To make an informed decision, it is necessary to collect the required data on time/cost/mistakes by monitoring the development process, and recording the appropriate information.
The variability of developer performance, and language/problem interaction means that it is necessary to monitor multiple development teams and multiple language/problem pairs, using statistical techniques to detect any language driven implementation performance differences.
How many development teams need to be monitored to reliably detect a performance difference driven by language used, given the variability of the major factors involved in the process?
If we assume that implementation times, for the same program, have a normal distribution (it might lean towards lognormal, but the maths is horrible), then there is a known formula. Three values need to be specified, and plug into this formula: the statistical significance (i.e., the probability of detecting an effect when none is present, say 5%), the statistical power (i.e., the probability of detecting that an effect is present, say 80%), and Cohen’s d; for an overview see section 10.2.
Cohen’s d is the ratio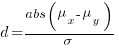 
, where 
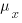and 
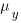is the mean value of the quantity being measured for the programs written in the respective languages, and 
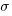is the pooled standard deviation.
Say the mean time to implement a program is 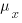, what is a good estimate for the pooled standard deviation, 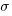, of the implementation times?
Having 66% of teams delivering within a factor of two of the mean delivery time is consistent with variation in LOC for the same program and estimation accuracy, and if anything sound slow (to me).
Rewriting the Cohen’s d ratio: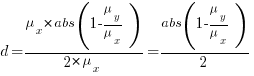 
If the implementation time when using language X is half that of using Y, we get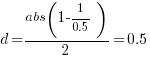 
. Plugging the three values into the pwr.t.test function, in R’s pwr package, we get:
> library("pwr")
> pwr.t.test(d=0.5, sig.level=0.05, power=0.8)
Two-sample t test power calculation
n = 63.76561
d = 0.5
sig.level = 0.05
power = 0.8
alternative = two.sided
NOTE: n is number in *each* group |
In other words, data from 64 teams using language X and 64 teams using language Y is needed to reliably detect (at the chosen level of significance and power) whether there is a difference in the mean performance (of whatever was measured) when implementing the same project.
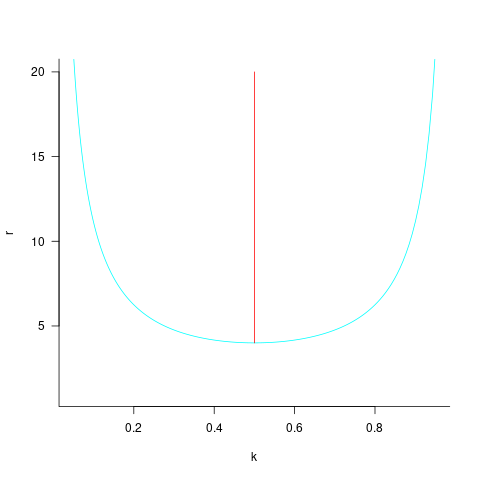
The plot below shows sample size required for a t-test testing for a difference between two means, for a range of X/Y mean performance ratios, with red line showing the commonly used values (listed above) and other colors showing sample sizes for more relaxed acceptance bounds (code):
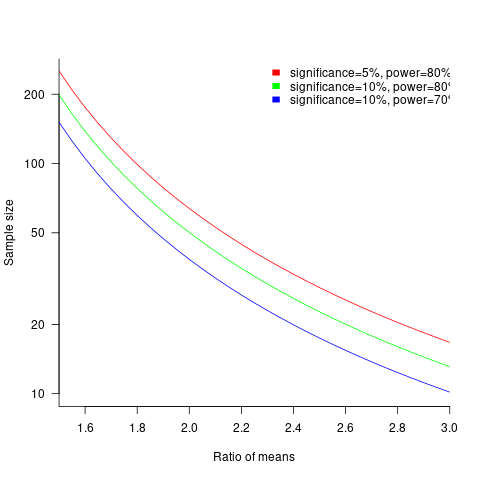
Unless the performance difference between languages is very large (e.g., a factor of three) the required sample size is going to push measurement costs into many tens of millions (£1 million per team, to develop a realistic application, multiplied by two and then multiplied by sample size).
For small programs solving certain kinds of problems, a factor of three, or more, performance difference between languages is not unusual (e.g., me using R for this post, versus using Python). As programs grow, the mundane code becomes more and more dominant, with the special case language performance gains playing an outsized role in story telling.
There have been studies comparing pairs of languages. Unfortunately, most have involved students implementing short problems, one attempted to measure the impact of programming language on coding competition performance (and gets very confused), the largest study I know of compared Fortran and Ada implementations of a satellite ground station support system.
The performance difference detected may be due to the particular problem implemented. The language/problem performance correlation can be solved by implementing a wide range of problems (using 64 teams per language).
A statistically meaningful comparison of the implementation costs of language pairs will take many years and cost many millions. This question is unlikely to every be answered. Move on.
My view is that, at least for the widely used languages, the implementation/maintenance performance issues are primarily driven by the ecosystem, rather than the language.
Criteria for increased productivity investment
You have a resource of 
person days to implement a project, and believe it is worth investing some of these days, 
, to improve team productivity (perhaps with training, or tooling). What is the optimal amount of resource to allocate to maximise the total project work performed (i.e., excluding the performance productivity work)?
Without any productivity improvement, the total amount of project work is:
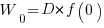, where 
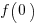is the starting team productivity function, f, i.e., with zero investment.
After investing person days to increase team productivity, the total amount of project work is now:
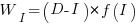, where 
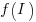is the team productivity function, f, after the investment .
To find the value of that maximises 
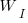, we differentiate with respect to , and solve for the result being zero:
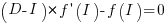, where 
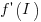is the differential of the yet to be selected function 
.
Rearranging this equation, we get:
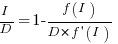
We can plug in various productivity functions, , to find the optimal value of .
For a linear relationship, i.e.,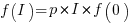 
, where 
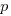is the unit productivity improvement constant for a particular kind of training/tool, the above expression becomes:
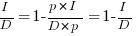
Rearranging, we get: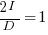 
, or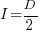 
.
The surprising (at least to me) result that the optimal investment is half the available days.
It is only worthwhile making this investment if it increases the total amount of project work. That is, we require: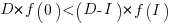 
.
For the linear improvement case, this requirement becomes:
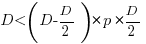, or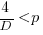 
This is the optimal case, but what if the only improvement options available are not able to sustain a linear improvement rate of at least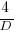 
? How many days should be invested in this situation?
A smaller investment,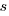 
, is only worthwhile when:
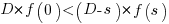, where 
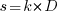, and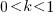 
.
Substituting gives: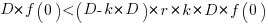 
, which simplifies to:
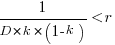
The blue/green line plot below shows the minimum value of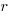 
for 
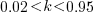(and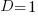 
, increasing moves the line down), with the red line showing the optimal value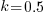 
. The optimal value of 
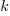is at the point where 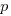has its minimum worthwhile value (the derivative of 
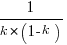is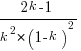 
; code):
This shows that it is never worthwhile making an investment when: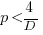 
, and that when 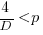it is always worthwhile investing 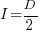, with any other value either wasting time or not extracting all the available benefits.
In practice, an investment may be subject to diminishing returns.
When the rate of improvement increases as the square-root of the number of days invested, i.e.,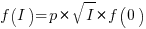 
, the optimal investment, and requirement on unit rate are as follows:
only invest: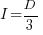 
, when: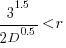 
If the rate of improvement with investment has the form: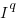 
, the respective equations are:
only invest: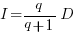 
, when: 
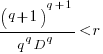. The minimal worthwhile value of 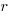always occurs at the optimal investment amount.
When the rate of improvement is logarithmic in the number of days invested, i.e.,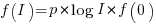 
, the optimal investment, and requirement on unit rate are as follows:
only invest: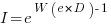 
, where 
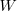is the Lambert W function, when: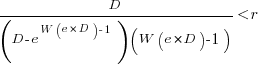 
These expressions can be simplified using the approximation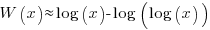 
, giving:
only invest: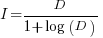 
, when: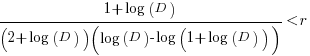 
In practice, after improving rapidly, further investment on improving productivity often produces minor gains, i.e., the productivity rate plateaus. This pattern of rate change is often modelled using a logistic equation, e.g.,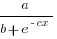 
.
However, following the process used above for this logistic equation produces an equation for , 
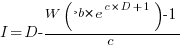, that does not have any solutions when 
and are positive.
The problem is that the derivative goes to zero too quickly. The Michaelis-Menten equation,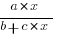 
, has an asymptotic limit whose derivative goes to zero sufficiently slowly that a solution is available.
only invest: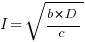 
, when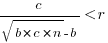 
The plot below shows example Michaelis-Menten and Logistic equations whose coefficients have been chosen to produce similar plots over the range displayed (code):
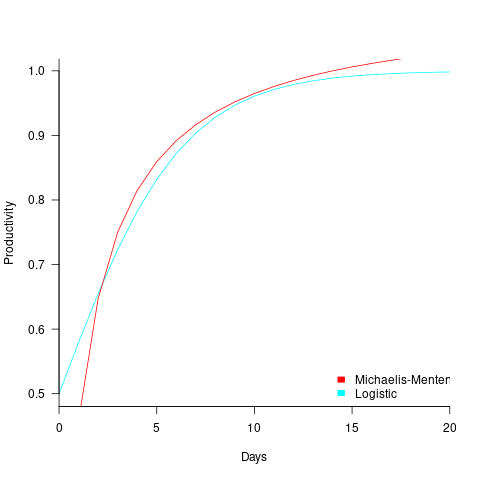
These equations are all well and good. The very tough problem of estimating the value of the coefficients is left to the reader.
This question has probably been answered before. But I have not seen it written down anywhere. References welcome.
Cost-effectiveness decision for fixing a known coding mistake
If a mistake is spotted in the source code of a shipping software system, is it more cost-effective to fix the mistake, or to wait for a customer to report a fault whose root cause turns out to be that particular coding mistake?
The naive answer is don’t wait for a customer fault report, based on the following simplistic argument: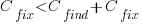 
.
where: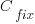 
is the cost of fixing the mistake in the code (including testing etc), and 
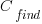is the cost of finding the mistake in the code based on a customer fault report (i.e., the sum on the right is the total cost of fixing a fault reported by a customer).
If the mistake is spotted in the code for ‘free’, then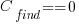 
, e.g., a developer reading the code for another reason, or flagged by a static analysis tool.
This answer is naive because it fails to take into account the possibility that the code containing the mistake is deleted/modified before any customers experience a fault caused by the mistake; let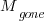 
be the likelihood that the coding mistake ceases to exist in the next unit of time.
The more often the software is used, the more likely a fault experience based on the coding mistake occurs; let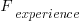 
be the likelihood that a fault is reported in the next time unit.
A more realistic analysis takes into account both the likelihood of the coding mistake disappearing and a corresponding fault being reported, modifying the relationship to: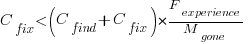 
Software systems are eventually retired from service; the likelihood that the software is maintained during the next unit of time,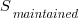 
, is slightly less than one.
Giving the relationship: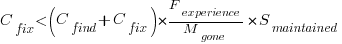 
which simplifies to: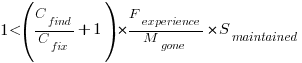 
What is the likely range of values for the ratio: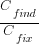 
?
I have no find/fix cost data, although detailed total time is available, i.e., find+fix time (with time probably being a good proxy for cost). My personal experience of find often taking a lot longer than fix probably suffers from survival of memorable cases; I can think of cases where the opposite was true.
The two values in the ratio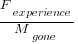 
are likely to change as a system evolves, e.g., high code turnover during early releases that slows as the system matures. The value of 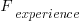should decrease over time, but increase with a large influx of new users.
A study by Penta, Cerulo and Aversano investigated the lifetime of coding mistakes (detected by several tools), tracking them over three years from creation to possible removal (either fixed because of a fault report, or simply a change to the code).
Of the 2,388 coding mistakes detected in code developed over 3-years, 41 were removed as reported faults and 416 disappeared through changes to the code: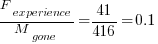 
The plot below shows the survival curve for memory related coding mistakes detected in Samba, based on reported faults (red) and all other changes to the code (blue/green, code+data):
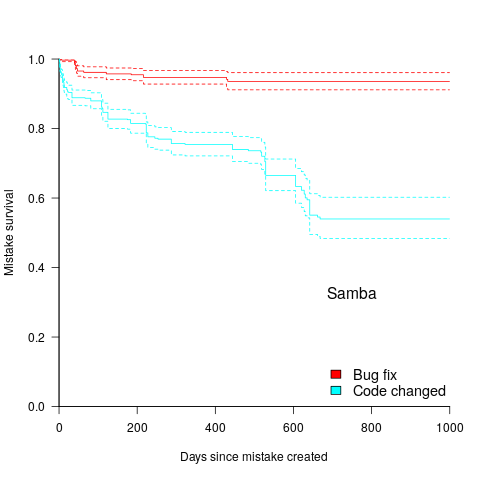
Coding mistakes are obviously being removed much more rapidly due to changes to the source, compared to customer fault reports.
For it to be cost-effective to fix coding mistakes in Samba, flagged by the tools used in this study (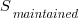 is essentially one), requires: 
.
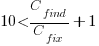Meeting this requirement does not look that implausible to me, but obviously data is needed.
Software engineering research problems having worthwhile benefits
Which software engineering research problems are likely to yield good-enough solutions that provide worthwhile benefits to professional software developers?
I can think of two (hopefully there are more):
- what is the lifecycle of software? For instance, the expected time-span of the active use of its various components, and the evolution of its dependency ecosystem,
- a model of the main processes involved in a software development project.
Solving problems requires data, and I think it is practical to collect the data needed to solve these two problems; here is some: application lifetime data, and detailed project data (a lot more is needed).
Once a good-enough solution is available, its practical application needs to provide a worthwhile benefit to the customer (when I was in the optimizing compiler business, I found that many customers were not interested in more compact code unless the executable was at least a 10% smaller; this was the era of computer memory often measured in kilobytes).
Investment decisions require information about what is likely to happen in the future, and an understanding of common software lifecycles is needed. The fact that most source code has a brief existence (a few years) and is rarely modified by somebody other than the original author, has obvious implications for investment decisions intended to reduce future maintenance costs.
Running a software development project requires an understanding of the processes involved. This knowledge is currently acquired by working on projects managed by people who have successfully done it before. A good-enough model is not going to replace the need for previous experience, some amount of experience is always going to be needed, but it will provide an effective way of understanding what is going on. There are probably lots of different good-enough ways of running a project, and I’m not expecting there to be a one-true-way of optimally running a project.
Perhaps the defining characteristic of the solution to both of these problems is lots of replication data.
Applications are developed in many ecosystems, and there is likely to be variations between the lifecycles that occur in different ecosystems. Researchers tend to focus on Github because it is easily accessible, which is no good when replications from many ecosystems are needed (an analysis of Github source lifetime has been done).
Projects come in various shapes and sizes, and a good-enough model needs to handle all the combinations that regularly occur. Project level data is not really present on Github, so researchers need to get out from behind their computers and visit real companies.
Given the payback time-frame for software engineering research, there are problems which are not cost-effective to attempt to answer. Suggestions for other software engineering problems likely to be worthwhile trying to solve welcome.
Recent Comments