Archive
Software companies in the UK
How many software companies are there in the UK, and where are they concentrated?
This question begs the question of what kinds of organization should be counted as a software company. My answer to this question is driven by the available data. Companies House is the executive agency of the British Government that maintains the register of UK companies, and basic information on 5,562,234 live companies is freely available.
The Companies House data does not include all software companies. A very small company (e.g., one or two people) might decide to save on costs and paperwork by forming a partnership (companies registered at Companies House are required to file audited accounts, once a year).
When registering, companies have to specify the business domain in which they operate by selecting the appropriate Standard Industrial Classification (SIC) code, e.g., Section J: INFORMATION AND COMMUNICATION, Division 62: Computer programming, consultancy and related activities, Class 62.01: Computer programming activities, Sub-class 62.01/2: Business and domestic software development. A company’s SIC code can change over time, as the business evolves.
Searching the description associated with each SIC code, I selected the following list of SIC codes for companies likely to be considered a ‘software company’:
62011 Ready-made interactive leisure and entertainment
software development
62012 Business and domestic software development
62020 Information technology consultancy activities
62030 Computer facilities management activities
62090 Other information technology service activities
63110 Data processing, hosting and related activities
63120 Web portals |
There are 287,165 companies having one of these seven SIC codes (out of the 1,161 SIC codes currently used); 5.2% of all currently live companies. The breakdown is:
All 62011 62012 62020 62030 62090 63110 63120 5,562,234 7,217 68,834 134,461 3,457 57,132 7,839 8,225 100% 0.15% 1.2% 2.4% 0.06% 1.0% 0.14% 0.15% |
Only one kind of software company (SIC 62020) appears in the top ten of company SIC codes appearing in the data:
Rank SIC Companies 1 68209 232,089 Other letting and operating of own or leased real estate 2 82990 213,054 Other business support service activities n.e.c. 3 70229 211,452 Management consultancy activities other than financial management 4 68100 194,840 Buying and selling of own real estate 5 47910 165,227 Retail sale via mail order houses or via Internet 6 96090 134,992 Other service activities n.e.c. 7 62020 134,461 Information technology consultancy activities 8 99999 130,176 Dormant Company 9 98000 118,433 Residents property management 10 41100 117,264 Development of building projects |
Is the main business of a company reflected in its registered SIC code?
Perhaps a company started out mostly selling hardware with a little software, registered the appropriate non-software SIC code, but over time there was a shift to most of the income being derived from software (or the process ran in reverse). How likely is it that the SIC code will change to reflect the change of dominant income stream? I have no idea.
A feature of working as an individual contractor in the UK is that there were/are tax benefits to setting up a company, say A Ltd, and be employed by this company which invoices the company, say B Ltd, where the work is actually performed (rather than have the individual invoice B Ltd directly). IR35 is the tax legislation dealing with so-called ‘disguised’ employees (individuals who work like payroll staff, but operate and provide services via their own limited company). The effect of this practice is that what appears to be a software company in the Companies House data is actually a person attempting to be tax efficient. Unfortunately, the bulk downloadable data does not include information that might be used to filter out these cases (e.g., number of employees).
Are software companies concentrated in particular locations?
The data includes a registered address for each company. This address may be the primary business location, or its headquarters, or the location of accountants/lawyers working for the business, or a P.O. Box address. The latitude/longitude of the center of each address postcode is available. The first half of the current postcode, known as the outcode, divides the country into 2,951 areas; these outcode areas are the bins I used to count companies.
Are there areas where the probability of a company being a software company is much higher than the national average (5.265%)? The plot below shows a heat map of outcode areas having a higher than average percentage of software companies (36 out of 2,277 outcodes were at least a factor of two greater than the national average; BH7 is top with 5.9 times more companies, then RG6 with 3.7 times, BH21 with 3.6); outcodes having fewer than 10 software companies were excluded (red is highest, green lowest; code+data):
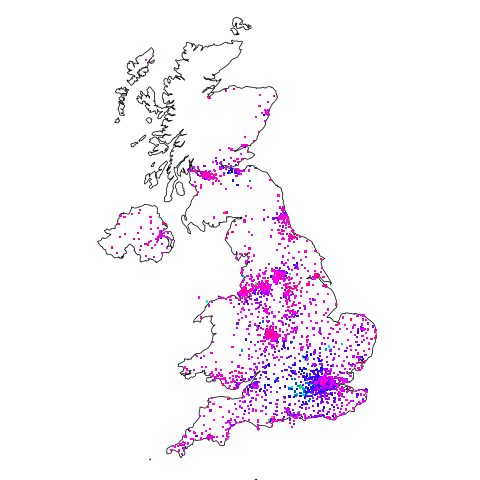
The higher concentrations are centered around the country’s traditional industrial towns and cities, with a cluster sprawling out from London. Cambridge is often cited as a high-tech region, but its highest outcode, CB4, is ranked 39th, at twice the national average (presumably the local high-tech is primarily non-software oriented).
Which outcode areas contain the most software companies? The following list shows the top ten outcodes, by number of registered companies (only BN3 and CF14 are outside London):
Rank Outcode Software companies
1 WC2H 10,860
2 EC1V 7,449
3 N1 6,244
4 EC2A 3,705
5 W1W 3,205
6 BN3 2,410
7 CF14 2,326
8 WC1N 2,223
9 E14 2,192
10 SW19 1,516 |
I’m surprised to see west-central London with so many software companies. Perhaps these companies are registered at their accountants/lawyers, or they are highly paid contractors who earn enough to afford accommodation in WC2. East-central London is the location of nearly all the computer companies I know in London.
Census of general purpose computers installed in the 1960s
In the 1960s a small number of computer manufacturers sold a relatively small number of general purpose computers (IBM dominated the market). Between 1962 and 1974 the magazine Computers and Automation published a monthly census listing the total number of installed, and unfilled orders for, general purpose computers. A pdf of all the scanned census data is available on Bitsavers.
Over the last 10-years, I have made sporadic attempts to convert the data in this pdf to csv form. The available tools do a passable job of generating text, but the layout of the converted text is often very different from the visible layout presented by a pdf viewer. This difference is caused by the pdf2text tools outputting characters in the order in which they occur within the pdf. For example, if a pdf viewer shows the following text, with numbers showing the relative order of characters within the pdf file:
1 2 6
3 7
4 5 8 |
the output from pdf2text might be one of the four possibilities:
1 2 1 2 1 1
3 3 2 2
4 5 4 3 3
6 5 4 5 4
7 6 6 5
8 7 7 6
8 8 7
8 |
One cause of the difference is the algorithm pdf2text uses to decide whether characters occur on the same line, i.e., do they have the same vertical position on the same page, measured in points (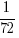 inch, or ≈ 0.353 mm)?
inch, or ≈ 0.353 mm)?
When a pdf is created by an application, characters on the same visual line usually have the same vertical position, and the extracted output follows a regular pattern. It’s just a matter of moving characters to the appropriate columns (editor macros to the rescue). Missing table entries complicate the process.
The computer census data comes from scanned magazines, and the vertical positions of characters on the same visual line are every so slightly different. This vertical variation effectively causes pdf2text to output the discrete character sequences on a variety of different lines.
A more sophisticated line assignment algorithm is needed. For instance, given the x/y position of each discrete character sequence, a fuzzy matching algorithm could assign the most likely row and column to each sequence.
The mupdf tool has an option to generate html, and this html contains the page/row/column values for each discrete character sequence, and it is possible to use this information to form reasonably laid out text. Unfortunately, the text on the scanned pages is not crisply sharp and mupdf produces o instead of 0, and l not 1, on a regular basis; too often for me to be interested in manually correctly the output.
Tesseract is the ocr tool of choice for many, and it supports the output of bounding box information. Unfortunately, running this software regularly causes my Linux based desktop to reboot.
I recently learned about Amazon’s Textract service, and tried it out. The results were impressive. Textract doesn’t just map characters to their position on the visible page, it is capable of joining multiple rows within a column and will insert empty strings if a column/row does not contain any characters. For instance, in the following image of the top of a page:

the column names are converted to "NAME OF MANUFACTURER","NAME OF COMPUTER", etc., and the empty first column/row are mapped to "".
The conversion is not quiet 100% accurate, but then the input is not 100% accurate; a few black smudges are treated as a single-quote or decimal point, and comma is sometimes treated as a fullstop. There were around 20 such mistakes in 11,000+ rows of numbers/names. There were six instances where two lines were merged into a single row, when the lines should have each been a separate row.
Having an essentially accurate conversion to csv available, does not remove the need for data cleaning. The image above contains two examples of entries that need to be corrected: the first column specifies that it is a continuation of a column on the previous page (over 12 different abbreviated forms of continued are used) Honeywell (cont'd) -> Honeywell, and other pages use a slightly different name for a particular computer DATA-matic 1000 -> Datamatic 1000. There are 350+ cleaning edits in my awk script that catch most issues (code+data).
How useful is this data?
Early computer census data in csv form is very rare, and now lots of it is available. My immediate use is completing a long-standing dataset conversion.
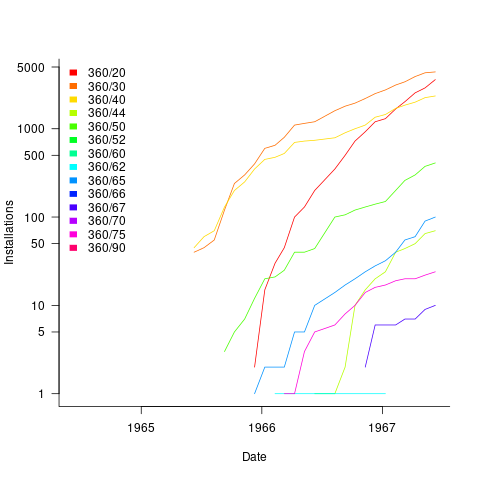
Obtaining the level of detail in this census, on a monthly basis, requires some degree of cooperation from the manufacturer. June 1967 appears to be the last time that IBM supplied detailed information, and later IBM census entries are listed as round estimates (and only for a few models).
The plot below shows the growth in the number of IBM 360 installations, for various models (unfilled orders date back to May 1964; code+data):
A paper to forget about
Papers describing vacuous research results get published all the time. Sometimes they get accepted at premier conferences, such as ICSE, and sometimes they even win a distinguished paper award, such as this one appearing at ICSE 2024.
If the paper Breaking the Flow: A Study of Interruptions During Software Engineering Activities had been produced by a final year PhD student, my criticism of them would be scathing. However, it was written by an undergraduate student, Yimeng Ma, who has just started work on a Masters. This is an impressive piece of work from an undergraduate.
The main reasons I am impressed by this paper as the work of an undergraduate, but would be very derisive of it as a work of a final year PhD student are:
- effort: it takes a surprisingly large amount of time to organise and run an experiment. Undergraduates typically have a few months for their thesis project, while PhD students have a few years,
- figuring stuff out: designing an experiment to test a hypothesis using a relatively short amount of subject time, recruiting enough subjects, the mechanics of running an experiment, gathering the data and then analysing it. An effective experimental design looks very simply, but often takes a lot of trial and error to create; it’s a very specific skill set that takes time to acquire. Professors often use students who attend one of their classes, but undergraduates have no such luxury, they need to be resourceful and determined,
- data analysis: the data analysis uses the appropriate modern technique for analyzing this kind of experimental data, i.e., a random effects model. Nearly all academic researchers in software engineering fail to use this technique; most continue to follow the herd and use simplistic techniques. I imagine that Yimeng Ma simply looked up the appropriate technique on a statistics website and went with it, rather than experiencing social pressure to do what everybody else does,
- writing a paper: the paper is well written and the style looks correct (I’m not an expert on ICSE paper style). Every field converges on a common style for writing papers, and there are substyles for major conferences. Getting the style correct is an important component of getting a paper accepted at a particular conference. I suspect that the paper’s other two authors played a major role in getting the style correct; or, perhaps there is now a language model tuned to writing papers for the major software conferences.
Why was this paper accepted at ICSE?
The paper is well written, covers a subject of general interest, involves an experiment, and discusses the results numerically (and very positively, which every other paper does, irrespective of their values).
The paper leaves out many of the details needed to understand what is going on. Those who volunteer their time to review papers submitted to a conference are flooded with a lot of work that has to be completed relatively quickly, i.e., before the published paper acceptance date. Anybody who has not run experiments (probably a large percentage of reviewers), and doesn’t know how to analyse data using non-simplistic techniques (probably most reviewers) are not going to be able to get a handle on the (unsurprising) results in this paper.
The authors got lucky by not being assigned reviewers who noticed that it’s to be expected that more time will be needed for a 3-minute task when the subject experiences an on-screen interruption, and even more time when for an in-person interruption, or that the p-values in the last column of Table 3 (0.0053, 0.3522, 0.6747) highlight the meaningless of the ‘interesting’ numbers listed
In a year or two, Yimeng Ma will be embarrassed by the mistakes in this paper. Everybody makes mistakes when they are starting out, but few get to make them in a paper that wins an award at a major conference. Let’s forget this paper.
Those interested in task interruption might like to read (unfortunately, only a tiny fraction of the data is publicly available): Task Interruption in Software Development Projects: What Makes some Interruptions More Disruptive than Others?
Finding reports and papers on the web
What is the best way to locate a freely downloadable copy of a report or paper on the web? The process I follow is outlined below (if you are new to this, you should first ask yourself whether reading a scientific paper will produce the result you are expecting):
- Google search. For the last 20 years, my experience is that Google search is the best place to look first.
Search on the title enclosed in double-quotes; if no exact matches are returned, the title you have may be slightly incorrect (variations in the typos of citations have been used to construct researcher cut-and-paste genealogies, i.e., authors copying a citation from a paper into their own work, rather than constructing one from scratch or even reading the paper being cited). Searching without quotes may return the desired result, or lots of unrelated matched. In the unrelated matches case, quote substrings within the title or include the first author’s surname.
The search may return a link to a ResearchGate page without a download link. There may be a “Request full-text” link. Clicking this sends a request email to one of the authors (assuming ResearchGate has an address), who will often respond with a copy of the paper.
A search may not return any matches, or links to copies that are freely available. Move to the next stage,
- Google Scholar. This is a fantastic resource. This site may link to a freely downloadable copy, even though a Google search does not. It may also return a match, even though a Google search does not. Most of the time, it is not necessary to include the title in quotes.
If the title matches a paper without displaying a link to a downloaded pdf, click on the match’s “Cited by” link (assuming it has one). The author may have published a later version that is available for download. If the citation count is high, tick the “Search within citing articles” box and try narrowing the search. For papers more than about five years old, you can try a “Customer range…” to remove more recent citations.
No luck? Move to the next stage,
- If a freely downloadable copy is available on the web, why doesn’t Google link to it?
A website may have a robots.txt requesting that the site not be indexed, or access to report/paper titles may be kept in a site database that Google does not access.
Searches now either need to be indirect (e.g., using Google to find an author web page, which may contain the sought after file), or targeted at specific cases.
It’s now all special cases. Things to try:
- Author’s website. Personal web pages are common for computing-related academics (much less common for non-computing, especially business oriented), but often a year or two out of date. Academic websites usually show up on a Google search. For new (i.e., less than a year), when you don’t need to supply a public link to the paper, email the authors asking for a copy. Most are very happy that somebody is interested in their work, and will email a copy.
When an academic leaves a University, their website is quickly removed (MIT is one of the few that don’t do this). If you find a link to a dead site, the Wayback Machine is the first place to check (try less recent dates first). Next, the academic may have moved to a new University, so you need to find it (and hope that the move is not so new that they have not yet created a webpage),
- Older reports and books. The Internet Archive is a great resource,
- Journals from the 1950s/1960s, or computer manuals. bitsavers.org is the first place to look,
- Reports and conference proceedings from before around 2000. It might be worth spending a few £/$ at a second hand book store; I use Amazon, AbeBooks, and Biblio. Despite AbeBooks being owned by Amazon, availability/pricing can vary between the two,
- A PhD thesis? If you know the awarding university, Google search on ‘university-name “phd thesis”‘ to locate the appropriate library page. This page will probably include a search function; these search boxes sometimes supporting ‘odd’ syntax, and you might have to search on: surname date, keywords, etc. Some universities have digitized thesis going back to before 1900, others back to 2000, and others to 2010.
The British Library has copies of thesis awarded by UK universities, and they have digitized thesis going back before 2000,
- Accepted at a conference. A paper accepted at a conference that has not yet occurred, maybe available in preprint form; otherwise you are going to have to email the author (search on the author names to find their university/GitHub webpage and thence their email),
- Both CiteSeer and then Semantic Scholar were once great resources. These days, CiteSeer has all but disappeared, and Semantic Scholar seems to mostly link to publisher sites and sometimes to external sites.
Dead-tree search techniques are a topic for history books.
More search suggestions welcome.
What is known about software effort estimation in 2024
It’s three years since my 2021 post summarizing what I knew about estimating software tasks. While no major new public datasets have appeared (there have been smaller finds), I have talked to lots of developers/managers about the findings from the 2019/2021 data avalanche, and some data dots have been connected.
A common response from managers, when I outline the patterns found, is some variation of: “That sounds about right.” While it’s great to have this confirmation, it’s disappointing to be telling people what they already know, even if I can put numbers to the patterns.
Some of the developer behavior patterns look, to me, to be actionable, e.g., send developers on a course to unbias their estimates. In practice, managers are worried about upsetting developers or destabilising teams. It’s easy for an unhappy developer to find another job (the speakers at the meetups I attend often end by saying: “and we’re hiring.”)
This post summarizes a talk I gave recently on what is known about software estimating; a video will eventually appear on the British Computer Society‘s Software Practice Advancement group’s YouTube channel, and the slides are on Github.
What I call the historical estimation models contain source code, measured in lines, as a substantial component, e.g., COCOMO which overfits a miniscule dataset. The problem with this approach is that estimates of the LOC needed to implement some functionality LOC are very inaccurate, and different developers use different LOC to implement the same functionality.
Most academic research in software effort estimation continues to be based on miniscule datasets; it’s essentially fake research. Who is doing good research in software estimating? One person: Magne Jørgensen.
Almost all the short internal task estimate/actual datasets contain all the following patterns:
- use of round-numbers (known as heaping in some fields). The ratios of the most frequently used round numbers, when estimating time, are close to the ratios of the Fibonacci sequence,
- short tasks tend to be under-estimated and long tasks over-estimate. Surprisingly, the following equation is a good fit for many time-based datasets:
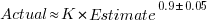 ,
, - individuals tend to either consistently over or under estimate (this appears to be connected with the individual’s risk profile),
- around 30% of estimates are accurate, 68% within a factor of two, and 95% within a factor of four; one function point dataset, one story point dataset, many time datasets,
- developer estimation accuracy does not change with practice. Possible reasons for this include: variability in the world prevents more accurate estimates, developers choose to spend their learning resources on other topics (such as learning more about the application domain).
I have a new ChatGPT generated image for my slide covering the #Noestimates movement:

The Whitehouse report on adopting memory safety
Last month’s Whitehouse report: BACK TO THE BUILDING BLOCKS: A Path Towards Secure and Measurable Software “… outlines two fundamental shifts: the need to both rebalance the responsibility to defend cyberspace and realign incentives to favor long-term cybersecurity investments.”
From the abstract: “First, in order to reduce memory safety vulnerabilities at scale, … This report focuses on the programming language as a primary building block, …” Wow, I never expected to see the term ‘memory safety’ in a report from the Whitehouse (not that I recall ever reading a Whitehouse report). And, is this the first Whitehouse report to talk about programming languages?
tl;dr They mistakenly to focus on the tools (i.e., programming languages), the focus needs to be on how the tools are used, e.g., require switching on C compiler’s memory safety checks which currently default to off.
The report’s intent is to get the community to progress from defence (e.g., virus scanning) to offence (e.g., removing the vulnerabilities at source). The three-pronged attack focuses on programming languages, hardware (e.g., CHERI), and formal methods. The report is a rallying call to the troops, who are, I assume, senior executives with no little or no knowledge of writing software.
How did memory safety and programming languages enter the political limelight? What caused the Whitehouse claim that “…, one of the most impactful actions software and hardware manufacturers can take is adopting memory safe programming languages.”?
The cited reference is a report published two months earlier: The Case for Memory Safe Roadmaps: Why Both C-Suite Executives and Technical Experts Need to Take Memory Safe Coding Seriously, published by an alphabet soup of national security agencies.
This report starts by stating the obvious (at least to developers): “Memory safety vulnerabilities are the most prevalent type of disclosed software vulnerability.” (one Microsoft reports says 70%). It then goes on to make the optimistic claim that: “Memory safe programming languages (MSLs) can eliminate memory safety vulnerabilities.”
This concept of a ‘memory safe programming language’ leads the authors to fall into the trap of believing that tools are the problem, rather than how the tools are used.
C and C++ are memory safe programming languages when the appropriate compiler options are switched on, e.g., gcc’s sanitize flags. Rust and Ada are not memory safe programming languages when the appropriate compiler options are switched on/off, or object/function definitions include the unsafe keyword.
People argue over the definition of memory safety. At the implementation level, it includes checks that storage is not accessed outside of its defined bounds, e.g., arrays are not indexed outside the specified lower/upper bound.
I’m a great fan of array/pointer bounds checking and since the 1980s have been using bounds checking tools to check my C programs. I found bounds checking is a very cost-effective way of detecting coding mistakes.
Culture drives the (non)use of bounds checking. Pascal, Ada and now Rust have a culture of bounds checking during development, amongst other checks. C, C++, and other languages have a culture of not having switching on bounds checking.
Shipping programs with/without bounds checking enabled is a contentious issue. The three main factors are:
- Runtime performance overhead of doing the checks (which can vary from almost nothing to a factor of 5+, depending on the frequency of bounds checked accesses {checks don’t need to be made when the compiler can figure out that a particular access is always within bounds}). I would expect the performance overhead to be about the same for C/Rust compilers using the same compiler technology (as the Open source compilers do). A recent study found C (no checking) to be 1.77 times faster, on average, than Rust (with checking),
- Runtime memory overhead. Adding code to check memory accesses increases the size of programs. This can be an issue for embedded systems, where memory is not as plentiful as desktop systems (recent survey of Rust on embedded systems),
- Studies (here and here) have found that programs can be remarkably robust in the presence of errors. Developers’ everyday experience is that programs containing many coding mistakes regularly behave as expected most of the time.
If bounds checking is enabled on shipped applications, what should happen when a bounds violation is detected?
Many bounds violations are likely to be benign, and a few not so. Should users have the option of continuing program execution after a violation is flagged (assuming they have been trained to understand the program message they are seeing and are aware of the response options)?
Java programs ship with bounds checking enabled, but I have not seen any studies of user response to runtime errors.
The reason that C/C++ is the language used to write so many of the programs listed in vulnerability databases is that these languages are popular and widely used. The Rust security advisory database contains few entries because few widely used programs are written in Rust. It’s possible to write unsafe code in Rust, just like C/C++, and studies find that developers regularly write such code and security risks exist within the Rust ecosystem, just like C/C++.
There have been various attempts to implement bounds checking in x86
processors. Intel added the MPX instruction, but there were problems with the specification, and support was discontinued in 2019.
The CHERI hardware discussed in the Whitehouse report is not yet commercially available, but organizations are working towards commercial products.
Extracting named entities from a change log using an LLM
The Change log of a long-lived software system contains many details about the system’s evolution. Two years ago I tried to track the evolution of Beeminder by extracting the named entities in its change log (named entities are the names of things, e.g., person, location, tool, organization). This project was pre-LLM, and encountered the usual problem of poor or non-existent appropriately trained models.
Large language models are now available, and these appear to excel at figuring out the syntactic structure of text. How well do LLMs perform, when asked to extract named entities from each entry in a software project’s change log?
For this analysis I’m using the publicly available Beeminder change log. Organizations may be worried about leaking information when sending confidential data to a commercially operated LLM, so I decided to investigate the performance of a couple of LLMs running on my desktop machine (code+data).
The LLMs I used were OpenAI’s ChatGPT plus (the $20 month service), and locally: Google’s Gemma (the ollama 7b model), a llava 7b model (llava-v1.5-7b-q4.llamafile), and a Mistral 7b model (mistral-7b-instruct-v0.2.Q8_0.llamafile). I used 7 billion parameter models locally because this is the size that is generally available for Open sourced models. There are a few models supporting the next step-up, at 13 billion parameters, and a few at 30 billion.
All the local models start a server at localhost:8080, and provide various endpoints. Mozilla’s llamafile based system is compatible with OpenAI’s python package openai. The documentation for the Gemma based system I installed uses the ollama package. In both cases, the coding required is trivial; just add a few statements to create a question based on command line input:
import openai import sys prefix='List the named entities in the following sentences: ' input_str=sys.argv[1] # change log entry from command line client = openai.OpenAI( base_url="http://localhost:8080/v1", # "http://<Your api-server IP>:port" api_key = "sk-no-key-required" ) stream = client.chat.completions.create( model="gpt-4", stream=True, temperature=0, seed=19, messages=[ {"role": "system", "content": "You are ChatGPT, an AI assistant. Your top priority is achieving user fulfilment via helping them with their requests."}, {"role": "user", 'content': prefix+ input_str } ] ) # Print response for chunk in stream: print(chunk.choices[0].delta.content or "", end="") print() |
How well did the models perform?
For rapid iteration, I used the web interface to ChatGPT. The responses started to appear within a few seconds and were displayed at a readable rate.
ChatGPT 3.5
When given a single change log entry, ChatGPT also provides a brief description of the named entity. In the following example, ‘twitter acct‘ and ‘blog posts‘ are not flagged as named entities:
User
print the named entities in the following quoted text "Created
this twitter acct to log user-visible improvements (UVIs) to
Beeminder. (Yes, this is a UVI. Everything counts no matter how
small!) Very first UVI! Back then this counted but nowadays we
don't count things that are too ancillary like making Twitter
accounts or writing blog posts. We did count a few UVIs for
creating this fancy changelog but decided that's too ancillary
now too."
ChatGPT
To identify named entities in the quoted text, we need to look for
proper nouns, which typically include names of specific people,
organizations, locations, and sometimes unique entities. In the
provided text, here are the named entities:
Beeminder - Refers to a specific service or product.
Twitter - Refers to a specific social media platform.
UVI (User-Visible Improvement) - Refers to a specific type of improvement.
changelog - Refers to a specific type of document or record. |
When asked to list the named entities in each of multiple lines, ChatGTP 3.5 performance drops. In the following response, the first line is identical to the example above; the response contains three, not four names entities. The second line contains named entities, but ChatGTP claims there are none. The response to the third line is accurate:
ChatGPT
Here are the named entities in each of the three lines:
"Created this twitter acct" line:
Twitter - Refers to a specific social media platform.
UVIs (User-Visible Improvements) - Refers to a specific
type of improvement.
Beeminder - Refers to a specific service or product.
"Added ridiculous dog-dressed-as-a-bee picture" line:
None
"Now suppressing reminder emails" line:
reminder emails - Refers to a specific type of communication.
bug fixes - Refers to a specific type of improvement aimed
at resolving software issues.
UVIs (User-Visible Improvements) - Refers to a specific
type of improvement. |
ChatGPT 4.0
ChatGPT 4.0 can handle multiple change log entries. The following is the response to the first three entries (the same three entries given the ChatGPT 3.5):
ChatGPT
To thoroughly identify the named entities within each line,
I'll systematically parse each one, focusing on extracting
specific types of entities such as organizations, people,
locations, dates, websites, and any other identifiable proper
nouns.
Beeminder, Twitter, UVI: Organizations or products.
dog-dressed-as-a-bee: Concept, not a proper noun but unique
enough to note.
reminder emails: Concept, referring to a feature. |
While it is possible to input 100 change log entries into the ChatGPT input box, the response contained no more than about 25 of them (there is a maximum limit on the number of input and output tokens).
Running locally
The machine I used locally contains 64G memory and an Intel Core i5-7600K running at 3.80GHz, with four cores. The OS is Linux Mint 21.1, running the kernel 5.15.0-76-generic. I don’t have any GPUs installed.
A GPU would probably significantly improve performance. On Amazon, the price of the NVIDIA Tesla A100 is now just under £7,000, an order of magnitude more than I am interested in paying (let alone the electricity costs). I have not seen any benchmarks comparing GPU performance on running LLMs locally, but then this is still a relatively new activity.
Overall, Gemma produced the best responses and was the fastest model. The llava model performed so poorly that I gave up trying to get it to produce reasonable responses (code+data). Mistral ran at about a third the speed of Gemma, and produced many incorrect named entities.
As a very rough approximation, Gemma might be useful. I look forward to trying out a larger Gemma model.
Gemma
Gemma took around 15 elapsed hours (keeping all four cores busy) to list named entities for 3,749 out of 3,839 change log entries (there were 121 “None” named entities given). Around 3.5 named entities per change log entry were generated. I suspect that many of the nonresponses were due to malformed options caused by input characters I failed to handle, e.g., escaping characters having special meaning to the command shell.
For around about 10% of cases, each named entity output was bracketed by “**”.
The table below shows the number of named entities containing a given number of ‘words’. The instances of more than around three ‘words’ are often clauses within the text, or even complete sentences:
# words 1 2 3 4 5 6 7 8 9 10 11 12 14 Occur 9149 4102 1077 210 69 22 10 9 3 1 3 5 4 |
A total of 14,676 named entities were produced, of which 6,494 were unique (ignoring case and stripping **).
Mistral
Mistral took 20 hours to process just over half of the change log entries (2,027 out of 3,839). It processed input at around 8 tokens per second and output at around 2.5 tokens per second.
When Mistral could not identify a named entity, it reported this using a variety of responses, e.g., “In the given …”, “There are no …”, “In this sentence …”.
Around 5.8 named entities per change log entry were generated. Many of the responses were obviously not named entities, and there were many instances of it listing clauses within the text, or even complete sentences. The table below shows the number of named entities containing a given number of ‘words’:
# words 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Occur 3274 1843 828 361 211 130 132 90 69 90 68 46 49 27 |
A total of 11,720 named entities were produced, of which 4,880 were unique (ignoring case).
A distillation of Robert Glass’s lifetime experience
Robert Glass is a software engineering developer, manager, researcher and author who, until six months ago, I had vaguely heard of; somehow I had missed reading any of his 25 books. After seeing citations to some of Glass’s books, I bought half-a-dozen or so, second hand. They are well written, and twenty-five years ago I would have found them very interesting; now I simply agree with the points made.
“software creativity 2.0” is Glass’s penultimate book, published in 2006, and the one that caught my attention. I would recommend his other books to anybody who is new to software engineering, or experienced people looking for an encapsulation in print of what they encounter at work.
Glass was 74 when this book was published, having started working in computing in 1954. He was there and seems to have met many of the major names in software engineering, working with some of them.
The book is a clear-eyed summary of what Glass has learned from being involved with software engineering, and watching method/tool fashions come and go. My favourite section draws parallels between software development cultures and the culture of Rome vs. Greek vs. Barbarian:
Models Roman Greek Barbarians Organization Organize people Organize things Barely Focus Manages projects Writes programs Leap to coding Motivation Group goals Problem to be solved Heroics Working style Organizations Small groups Solo Politics Imperial Democratic Anarchist Tool use People are tools Things are tools Avoid tools Status Function-ocracy Meritocracy Fear-ocracy Activities Plan things Do things Break things Emphasize Form Substance Line of code |
The contents are essentially a collection of short essays, organized under the 19 chapter headings below, which in turn are grouped into four parts. The first nine chapters (part I, and 60% of pages) contain the experience based material, with the subsequent parts/pages having a creativity theme. A thread running through the discussion is idealism/practice:
Discipline vs. Flexibility
Formal methods versus Heuristics
Optimizing versus Satisficing
Quantitative versus Qualitative Reasoning
Process versus Product
Intellect vs. Clerical Tasks
Theory vs. Practice
Industry vs. Academe
Fun versus Getting Serious
Creativity in the Software Organization
Creativity in Software Technology
Creative Milestones in Software History
Organizational Creativity
The Creative Person
Computer Support for Creativity
Creativity Paradoxes#'twas Always Thus
A Synergistic Conclusion
Other Conclusions |
This book deserves to be widely read. I found it best to read a single section per sitting.
Some information on story point estimates for 16 projects
Issues in Jira repositories sometimes include an estimate, in story points, but no information on time to complete (an opening/closing date is usually available; in some projects issues pass through various phases, and enter/exit date/time may be available).
Evidence-based software engineering is a data driven approach to figuring out software development processes. At the practical level, data is usually hard to come by; working with whatever data is available, an analysis may feel like making a prophecy based on examining animal entrails.
Can anything be learned from project issue data that just contains story point estimates? Let’s go on a fishing expedition.
My software data collection includes a paper that collected 23,313 story point estimates from 16 projects (the authors tried to predict an estimate, in story points, for an issue based on its description). If nothing else, this data is a sample of what might be encountered in other projects.
Developers estimating with story points often select values from the Fibonacci sequence, while developers estimating using hours/minutes often use round numbers. The granularity of both the Fibonacci values and round numbers follow the same exponential growth pattern. In terms of granularity, estimating story points in Fibonacci values need not far removed from estimating time in round numbers.
The number of story points per project varied from 352 to 4,667, with a mean of 1,457.
The plots below show the number of issues (y-axis, normalised across projects) estimated to require a given number of story points (x-axis), for 16 projects, with projects clustered by peak story point value (i.e., a project’s most frequently used story point value; code+data):
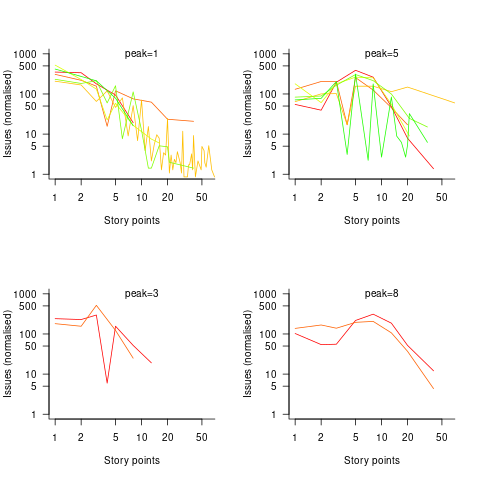
Are the projects with estimate peaks at 3 and 8 story points a quirk of this dataset, or is it to be expected that around 10% of projects will peak at one of these values?
For me, what jumps out of these plots is the number and extent of 4 story point estimates. Perhaps it’s just a visual effect, the actual number is an order of magnitude less than for 3 and 5 story points.
The plot below shows the percentage of estimated story points that are not Fibonacci numbers, sorted by project (the one project not showing has 0%; code+data):
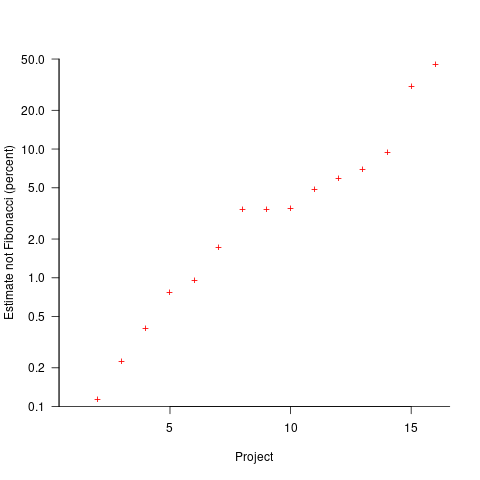
If nothing else, these plots provide a base to start from, and potentially claim to have seen this pattern before.
Why did organizations fund the creation of the first computers?
What were the events that drove organizations to fund the creation of the first computers?
I suspect that many readers do not appreciate how long scientific/engineering calculations took before electronic computers became available, or the huge number of clerical staff employed to process the paperwork associated with running any sizeable business.
If somebody wanted to know the logarithm of some value, or the sine/cosine of an angle, they looked up the answer in a table. Individuals owned small booklets of tables supplying some level of granularity and number of significant digits. My school boy booklet contains 60-pages of tables, all to five digits of output accuracy, with logarithm supporting four-digit input values and the sine/cosine/tangent tables having an input granularity of hundredth of a degree.
The values in these tables were calculated by human computers; with the following being among the most well known (for more details, see Calculation and Tabulation in the Nineteenth Century: Airy versus Babbage by Doron Swade, and The History of Mathematical Tables: from Sumer to Spreadsheets edited by Campbell-Kelly, Croarken, Flood, and Robson):
- In 1624 Henry Briggs published logarithms for the integer ranges 1-20,000 and 90,001-100,000 (to 14 decimal places), followed some years later by tables of sine and logarithm of sine; in 1628 Adriaan Vlacq publishing tables that filled in the missing values (to 10 decimal places). In 1783 Jurij Vega published a bug-fixed and extended version of Vlacq’s tables.
In 1827 Charles Babbage (that Babbage) published Table of Logarithms of the Natural Numbers from 1 to 10800. These tables were based on corrected versions of these tables, a rigorous nine-stage proofreading process was followed to prevent new mistakes creeping in.
Today, one person can publish A reconstruction of the tables of Briggs’ Arithmetica logarithmica (1624), with an appendix containing 300 pages of calculated values,
- between 1794 and 1799, Gaspard de Prony employed sixty to eighty computers to calculate the logarithms of the integers from 1 to 200,000 to fifteen significant digits (rounding issues sometimes required calculating 25 decimal digits; published in eighteen volumes). Around 400 man-years.
Logarithms and trigonometric functions are very widely used, creating incentives for investing in calculating and publishing tables. While it may be financially worthwhile investing in producing tables for some niche markets (e.g. Life tables for insurance companies), there is an unmet demand that will only be filled by a dramatic drop in the cost of computing simple expressions.
Babbage’s Difference engine was designed to evaluate polynomial expressions and print the results; perfect for publishing tables. While Babbage did not build a Difference engine, starting in 1837, engines based on Babbage’s design were built and sold commercially by the Swede Per Georg Scheutz.
Mechanical calculators improve accuracy and speed the process up. Vacuum tubes are invented in 1904 and become widely used to process analogue signals. World War II created an urgent demand for the results of a variety of time-consuming calculations, e.g., accurate ballistic tables, and valve computers were built. The plot below shows the cost per million operations for manual, mechanical and valve computers (code+data):
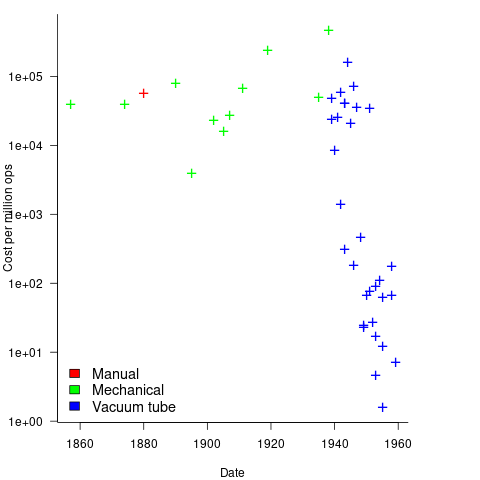
To many observers at the start of the 1950s, the market for electronic computers appeared to be organizations who needed to perform large amounts of scientific/engineering calculation.
Most businesses perform simple calculations on many unrelated values, e.g., banks have to credit/debit the appropriate account when money is deposited/withdrawn. There is no benefit in having a machine that can perform hundreds of calculations per second unless it can be fed data fast enough to keep it busy.
It so happened that, at the start of the 1950s, the US banking system was facing a crisis, the growth in the number of cheques being written meant that it would soon take longer than one day to process all the cheques that arrived in one day. In 1950 Bank of America managed 4.6 million checking accounts, and were opening 23,000 new account per month. Bank of America was then the largest bank in the world, and had a keen interest in continued growth. They funded the development of a bespoke computer system for processing cheques, the ERMA Banking system, which went live in 1959. The plot below shows the number of cheques processed per year by US banks (code+data):
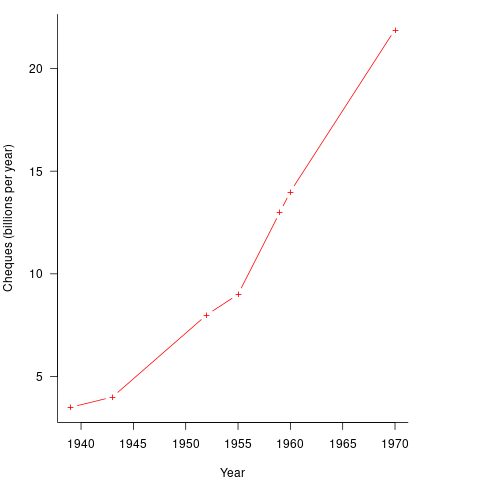
The ERMA system included electronic storage for holding account details, and data entry was speeded up by encoding account details on a magnetic strip included within every cheque.
Businesses are very interested in an integrated combination of input devices plus electronic storage plus compute. There are more commerce oriented businesses than scientific/engineering businesses, and commercial businesses usually have a lot more money to spend, i.e., the real money to be made by selling computers was the business data processing market.
The plot below shows the decreasing cost of hard disc storage (blue, right axis), along with the decreasing computing cost of valve based computers (red, left axis; code+data):
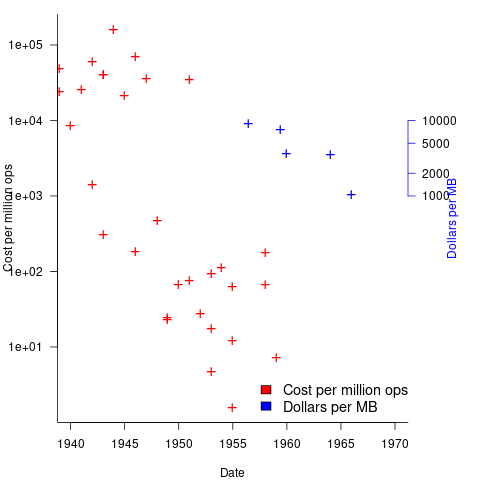
There was a larger business demand to be able to store information electronically, and the hard disc was invented by IBM, roughly 15 years after the first electronic computers.
The very different application demands of data processing and scientific/engineering are reflected in the features supported by the two languages designed in the 1950s, and widely used for the rest of the century: Cobol and Fortran.
Data processing involves simple operations on large quantities of data stored in a potentially huge number of different combinations (the myriad of mechanical point-of-sale terminals stored data in a myriad of different formats, which evolved over time, and the demand for backward compatibility created spaghetti data well before spaghetti code existed). Cobol has extensive functionality supporting the layout and format of input and output data, and simplistic coding constructs.
Scientific/engineering code involves complex calculations on some amount of input. Fortran has extensive functionality supporting program control flow, and relatively basic support for data input/output.
A third major application domain is real-time processing, such as SAGE. However, data on this domain is very hard to find, so it is not discussed.
Recent Comments