Archive
The units of measurement for software reliability
How do the people define software reliability? One answer can be found by analyzing defect report logs: one study found that 42.6% of fault reports were requests for an enhancement, changes to documentation, or a refactoring request; a study of NASA spaceflight software found that 63% of reports in the defect tracking system were change requests.
Users can be thought of as broadly defining software reliability as the ability to support current (i.e., the software works as intended) and future needs (i.e., functionality that the user does not yet know they need, e.g., one reason I use R, rather than Python, for data analysis, is because I believe that if a new-to-me technique is required, a package+documentation supporting this technique is more likely to be available in R).
Focusing on current needs, the definition of software reliability depends on the perspective of who you ask, possibilities include:
- commercial management: software reliability is measured in terms of cost-risk, i.e., the likelihood of losing an amount £/$ as a result of undesirable application behavior (either losses from internal use, or customer related losses such as refunds, hot-line support, and good will),
- Open source: reliability has to be good enough and at least as good as comparable projects. The unit of reliability might be fault experiences per use of the program, or the number of undesirable behaviors encountered when processing pre-existing material,
- user-centric: mean time between failure per uses of the application, e.g., for a word processor, documents written/edited. For compilers, mean time between failure per million lines of source translated,
- academic and perhaps a generic development team: mean time between failure per million lines/instructions executed by the application. The definition avoids having to deal with how the software is used,
- available data: numeric answers require measurement data to feed into a calculation. Data that is relatively easy to collect is cpu time consumed by tests that found some number of faults, or perhaps wall time, or scraping the bottom of the barrel the number of tests run.
If an organization wants to increase software reliability, they can pay to make the changes that increase reliability. Pointing this fact out to people can make them very annoyed.
Student projects for 2024/2025
It will soon be that time of year when university students are looking for an interesting idea for a project. On an irregular basis, I post some ideas for thesis projects (here and here); primarily for students studying computing. In a change of direction, this post suggests software related ideas for business student projects.
Two idea areas require data analysis skills, one requires people skills, and one an interest in theory.
More suggestions welcome in the comments.
Career paths in software
Organizations employ people to work on software systems. What is the career path of people who work on software systems? Question include: how long people stay in a particular job or company, and salary changes over time (the only data I know of investigates the career paths of 500 people working in IT).
Governments are interested in employment, and they collect and publish data at various levels of granularity. The US Bureau of Labor Statistics contains a vast amount of information, but finding the bits of interest can require a lot of work.
In the US, government employee salary is public information, and various sites make this available, e.g., OpePayrolls and Transparent California. There is a Japanese Open Salaries, and various commercial companies operate an open salary policy (Buffer is perhaps the most famous).
This project requires students with some data analysis skills.
There is some data on job postings,
Computer company lifecycle
Companies are born, do business and eventually die (unless bought/merged). How do the lifecycle characteristics of computer companies differ from companies doing business in other domains? Lifecycle characteristics of interest might include profiles of age, number of employees, and profitability. What are the consequences, if any, of these differences?
Details of all UK registered companies are freely available from Companies House.
Open Corporates provides company information from across the world, but it is not free in bulk.
Some analysis of the geographical clustering of software companies in the UK.
This project requires students with some data analysis skills.
AI startup ecosystem
AI has exploded on the tech scene, and lots of people are creating startups to build services/products around LLMs. Teams are very fluid, with people moving around a lot looking for a viable service/product. Sometimes these teams form companies, and these might eventually leave stealth mode and become visible. What are the characteristics of the AI startup ecosystem within a city; questions include: how many people are working within it, their backgrounds, and the business areas are they focusing on?
This project requires students with people skills and a willingness to get out and about. Much of the current AI ecosystem is only visible to those within it. Evening meetups and workshops offer a way into this personal network. This research involves bootstrapping the data gathering by spending evenings schmoozing with founders and their new hires, and is probably only practical in major cities with a very active tech meeting scene.
An analysis of a Dutch software business network.
Theoretical analysis
Those with an interest in theory might like to analyse cost-benefit decision-making within software development. Examples of simple analysis+supporting data include:
Analysis of when refactoring becomes cost-effective, and Cost-effectiveness decision for fixing a known coding mistake, and Break even ratios for development investment decisions
Memory bandwidth: 1991-2009
The Stream benchmark is a measure of sustained memory bandwidth; the target systems are high performance computers. Sustained in the sense of distance running, rather than a short sprint (the term for this is peak memory bandwidth and occurs when the requested data is in cache), and bandwidth in the sense of bytes of memory read/written per second (implemented using chunks the size of a double precision floating-point type). The dataset contains 1,018 measurements collected between 1991 and 2009.
The dominant characteristic of high performance computing applications is looping over very large arrays, performing floating-point operations on all the elements. A fast floating-point arithmetic unit has to be connected to a memory subsystem that can keep it fed with new floating-point values and write back computed values.
The Stream benchmark, in Fortran and C, defines several arrays, each containing max(1e6, 4*size_of_available_cache) double precision floating-point elements. There are four loops that iterate over every element of the arrays, each loop containing a single statement; see Fortran code in the following table (q is a scalar, array elements are usually 8-bytes, with add/multiply being the floating-point operations):
Name Operation Bytes FLOPS Copy a(i) = b(i) 16 0 Scale a(i) = q*b(i) 16 1 Sum a(i) = b(i) + c(i) 24 1 Triad a(i) = b(i) + q*c(i) 24 2 |
A system’s memory bandwidth will depend on the speed of the DRAM chips, the performance of the devices that transport bytes to the cpu, and the ability of the cpu to handle incoming traffic. The Stream data contains 21 columns, including: the vendor, date, clock rate, number of cpus, kind of memory (i.e., shared/distributed), and the bandwidth in megabytes/sec for each of the operations listed above.
How does the measured memory bandwidth change over time?
For most of the systems, the values for each of Copy, Scale, Sum, and Triad are very similar. That the simplest statement, Copy, is sometimes a bit faster/slower than the most complicated statement, Triad, shows that floating-point performance is much smaller than the time taken to read/write values to memory; the performance difference is random variation.
Several fitted regression models explain over half of the variance in the data, with the influential explanatory variables being: clock speed, date, type of system (i.e., PC/Mac or something much more expensive). The plot below shows MB/sec for the Copy loop, with three fitted regression models (code+data):
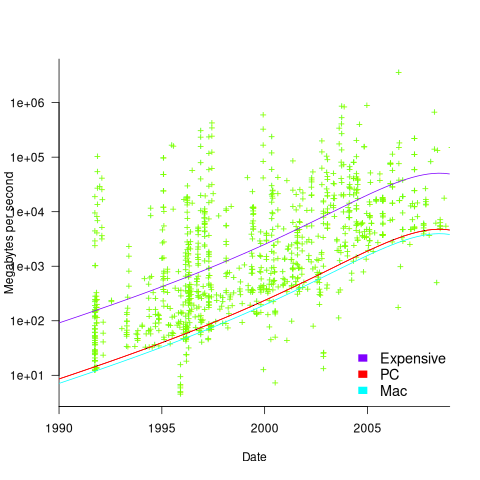
Fitting these models first required fitting a model for cpu clock rate over time; predictions of mean clock rate over time are needed as input to the memory bandwidth model. The three bandwidth models fitted are for PCs (189 systems), Macs (39 systems), and the more expensive systems (785; the five cluster systems were not fitted).
There was a 30% annual increase in memory bandwidth, with the average expensive systems having an order of magnitude greater bandwidth than PCs/Macs.
Clock rates stopped increasing around 2010, but go faster DRAM standards continue to be published. I assume that memory bandwidth continues to increase, but that memory performance is not something that gets written about much. The memory bandwidth on my new system is 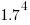 MB/sec. This 2024 sample of one is 3.5 times faster than the average 2009 PC bandwidth, which is 100 times faster than the 1991 bandwidth.
MB/sec. This 2024 sample of one is 3.5 times faster than the average 2009 PC bandwidth, which is 100 times faster than the 1991 bandwidth.
The LINPACK benchmarks are the traditional application oriented cpu benchmarks used within the high performance computer community.
The 2024 update to my desktop system
I have just upgraded my desktop system. As you can see from the picture below, it is a bespoke system; the third system built using the same chassis.

The 11 drive bays on the right are configured for six 5.25-inch and five 3.5-inch disks/CD/DVD/tape drives, there is a drive cage that fits above the power supply (top left) that holds another three 3.5-inch devices. The central black rectangle with two sets of four semicircular caps (fan above/below) is the cpu cooling tower, with two 32G memory sticks immediately to its right. The central left fan is reflected in a polished heatsink.
Why so many bays for disks?
The original need, in 2005 (well before GitHub), was for enough storage to hold the source code available, via ftp, from various hosting sites that were springing up, hence the choice of the Thermaltake Armour Series VA8000BWS Supertower. The first system I built contained six 400G Barracuda drives
The original power supply, a Thermaltake Silent Purepower 680W PSU, with its umpteen power connectors is still giving sterling service (black box with black fan at top left).
When building a system, I start by deciding on the motherboard. Boards supporting 6+ SATA connectors were once rare, but these days are more common on high-end systems. I also look for support for the latest cpu families and high memory bandwidth. I’m not a gamer, so no interest in graphics cards.
The three systems are:
- in 2005, an ASUS A8N-SLi Premium Socket 939 Motherboard, an AMD Athlon 64 X2 Dual-Core 4400 2.2Ghz cpu, and Corsair TWINX2048-3200C2 TwinX (2 x 1GB) memory. A Red Hat Linux distribution was installed,
- in 2013, an intermittent problem appeared on the A8N motherboard, so I upgraded to an ASUS P8Z77-V 1155 Socket motherboard, an Intel Core i5 Ivy Bridge 3570K – 3.4 GHz cpu, and Corsair CMZ16GX3M2A1600C10 Vengeance 16GB (2x8GB) DDR3 1600 MHz memory. Terabyte 3.25-inch disk drives were now available, and I installed two 2T drives. A openSUSE Linux distribution was installed.
The picture below shows the P8Z77-V, with cpu+fan and memory installed, sitting in its original box. This board and the one pictured above are the same length/width, i.e., the ATX form factor. This board is a lot lighter, in color and weight, than the Z790 board because it is not covered by surprisingly thick black metal plates, intended to spread areas of heat concentration,

- in 2024, there is no immediate need for an update, but the 11-year-old P8Z77 is likely to become unreliable sooner rather than later, better to update at a time of my choosing. At £400 the ASUS ROG Maximus Z790 Hero LGA 1700 socket motherboard is a big step up from my previous choices, but I’m starting to get involved with larger datasets and running LLMs locally. The Intel Core i7-13700K was chosen because of its 16 cores (I went for a hefty cooler upHere CPU Air Cooler with two fans), along with Corsair Vengeance DDR5 RAM 64GB (2x32GB) 6400 memory. A 4T and 8T hard disk, plus a 2T SSD were added to the storage system. The Linux Mint distribution was installed.
The last 20-years has seen an evolution of the desktop computer I own: roughly a factor of 10 increase in cpu cores, memory and storage. Several revolutions occurred between the roughly 20 years from the first computer I owned (an 8-bit cpu running at 4 MHz with 64K of memory and two 360K floppy drives) and the first one of these desktop systems.
What might happen in the next 20-years?
Will it still be commercially viable for companies to sell motherboards? If enough people switch to using datacenters, rather than desktop systems, many companies will stop selling into the computer component market.
LLMs perform simple operations on huge amounts of data. The bottleneck is transferring the data from memory to the processors. A system where simple compute occurs within the memory system would be a revolution in mainstream computer architecture.
Motherboards include a socket to support a specialised AI chip, like the empty socket for Intel’s 8087 on the original PC motherboards, is a reuse of past practices.
A new NASA software dataset from the 1970s
When modeling the process of software development, to optimise the creation of new projects, the best measurement data to use are those relating to whatever developers are doing today.
Unfortunately, measurement data for software engineering processes is very hard to find; few development groups record anything about what they do, and even when they do the files are rarely kept.
Anybody involved in evidence-based software engineering has to be willing to work with whatever data is available, even when it is for software systems built decades ago.
The usefulness of any measurement data, ancient or recent, is dependent on its relevance to the questions being analysed.
During a recent search for the DACS dataset, I found measurement data for 29 software projects contained in a 1981 NASA report. While the projects happened decades ago (1975-1981) for a niche application (software for spacecraft), the measurement data is much more extensive than usual, containing background information on many of the projects; given the rarity of software project data from this period, the 47 rows of data on each project, in Table 3.1-1, looked interesting enough to extract and analyse (output from Amazon’s usually robust Textract needed some hours of manual post-processing; code+data).
While this data is not of immediate use, I will invariably get involved in a discussion, or analysis, where this dataset will be a big improvement on nothing.
Are there any points to note?
- there is a linear relationship between the totals of programmer hours and management hours, with an average of 4.4 programmer hours per management hour. This sounds low, but these projects are developing embedded software and there are likely to be many stakeholders,
- the average percentage of time spent in each phase of the Waterfall process used was: Design 31%, Code-Test 29%, System testing 11%, Acceptance testing 10%, Cleanup 20%. Lots of testing is to be expected for spacecraft software,
- the average number of project source lines was 34k. I don’t know whether this is high or low, NASA press releases invariably cite the total amount of code on the spacecraft.
It’s worth noting that this small dataset is of a size and project detail that was used by researchers in the 1970s/1980s to validate software theories that are still with us today, e.g., the COCOMO estimation model, the McCabe metrics were not validated on any data, and the Halstead metrics were checked using multiple datasets each of similar size. I suspect that many of these datasets also came from DOD or NASA projects.
Program fault reports are caused by its users
Faults are generated by users of the software; no users, no fault reports. Fault reports will be generated for software that is free of coding mistakes; one study found that 42.6% of fault reports were misclassified as either requests for an enhancement, changes to documentation, or a refactoring request, or not requiring changes to the code; a study of NASA spaceflight software found that 63% of reports in the defect tracking tool were change requests.
Is the number of reported faults proportional to the number of users, the log of the number of users, or perhaps it depends on the application, or who knows what?
Some users will only use some features, others other features. Some users will be occasional users, while some will be heavy users.
There are a handful of fault report datasets containing measurements of software usage. The largest, and most widely cited, is “Optimizing Preventive Service of Software Products” by E. N. Adams. The data is this paper lists the number of faults reported in eight time intervals (20 to 50,000 months), for nine applications running on IBM mainframes between 1975 and 1980. Traditionally, the licensing for many Mainframe applications charge customers a fee based on their usage. Does this usage data still exist? Perhaps there is some sitting on a shelf in court documents. Pointers to possible cases most welcome.
Early papers on software testing sometimes measured the amount of cpu, or elapsed time, between each fault experience. However, the raw data was rarely published.
Data is available, for the Debian and Ubuntu distributions, on the number of installs for each application (counts rely on local machine sending information on installs, which is now an opt-in process for Ubuntu).
The following analysis uses data from the paper Impact of Installation Counts on Perceived Quality: A Case Study on Debian by Herraiz, Shihab, Nguyen, and Hassan, and the Ubuntu popularity project.
The plot below shows the number of reported faults against number of installs for the 14,565 programs in the “wheezy” Debian release; red line is the fitted power law: 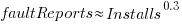 (code+data):
(code+data):
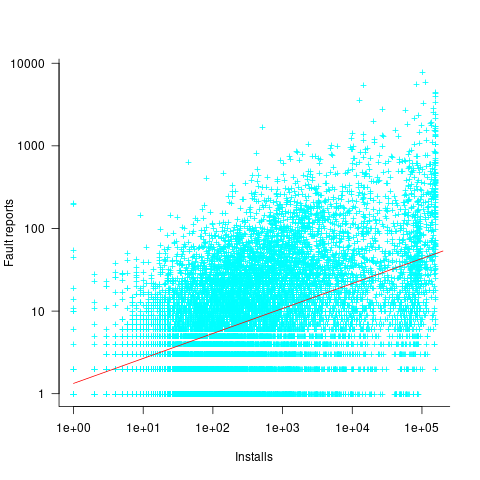
The huge variability in the number of fault reports for a given number of installs is likely driven by variability in the usage of the installed programs (or even no usage; I installed ImageMagick purely to use its convert program), the propensity of users of particular programs to report fault experiences (which in turn depends on the need for a fix, and the ease of reporting), and the number of coding faults in the source code.
The Debian installs/faults data does not include any usage information, however, the Ubuntu popularity data includes not only a count of installs, but the corresponding counts of regular users and non-usages. Given that Ubuntu is a fork of Debian, and has substantial usage, I’m assuming that the user base is sufficiently similar that the Ubuntu usage data at the time of the “wheezy” release can be applied to the “wheezy” Debian install/fault data.
The plot below shows, for 220,309 programs, the fraction of installs that are regularly used against the corresponding number of installs. The left-most line running top-left to bottom-right shows programs regularly used by one install, next line two regular users, etc (code+data):

Using the merged, by program name, Ubuntu usage/Debian fault counts, I built several regression models, along with plotting the data/fits. The quality of the models was worse than the original Debian model 🙁 . Two possibilities that spring to mind are: the correlation between usage and fault reports only becomes visible when the counts are divided into short periods (perhaps a year?), or the correlation is very weak. It is probably going to take a lot of time to work through this.
Confidence intervals: my one recommended practice
What recommended practices should developers/managers follow when analysing data they have collected/available?
The scientific approach to data analysis mandates specifying a hypothesis before gathering the data, let alone analysing it. This approach has proven workable when researchers are familiar with an evidence-based body of knowledge. In this environment it’s acceptable, even required, to criticise anyone who analyses data without having a hypothesis and just follow along where ever the data appears to lead.
In fields lacking an evidence-based body of knowledge, such as software engineering (which does have an extensive body of folklore), it can be difficult to articulate a reasonable set of hypothesis to test against, before analysing the date. Time and cost are the incentives that push developers/managers in to simply following the data where ever it leads them:
- understandably, they are only interested in solving their own local problem, not building global theories of software engineering practices,
- as occasional data analysts, developers/managers probably have little or no experience in formulating hypothesis, and don’t have the time to become familiar with the existing evidence around the processes of interest,
- formulating a hypothesis, along with its associated model of the world, can require a surprising amount of work, often involving many interacting factors to consider (an ad-hoc approach based on an evolving analysis of data can appear to need a lot less effort).
Following the data can feel like the agile approach to data analysis. However, thoughtlessly following the data is fraught with dangers, particularly with small sample sizes (while there are often copious quantities of source, the human side of software engineering often involves miniscule sample sizes). It has always been difficult to get developers to slow down and think when writing code, it seems unrealistic to expect habits to change for data analysis.
I take a somewhat schizophrenic approach in my workshop for software developers, with many slides illustrating the dangers of just jumping in, along with other slides showing how to quickly find patterns in data (the main topic of conversation during the hands-on sessions).
My one recommended practice is that confidence intervals be calculated and included in the presented results. Why just one recommendation? I think recommendations involving sample size, hypothesis, thinking hard, etc will be ignored. Results showing wide confidence intervals highlight a range of possible problems: insufficient sample sizes, along with marginal effects and other uncertainties.
The scientific recommendation approach would be to use p-values. The problem with these is that they will probably have to be explained to developers/managers, who will have little idea about how to interpret them.
The presence of confidence intervals in a summary of results is a major step up from current practices. My experiences with developer/manager driven data analysis include:
- using data, that happens to be available, that has no connection to the questions of interest,
- collecting data, but fail to extract much information (because primitive analysis techniques were used). This situation is also very common in software engineering research papers,
- selling an idea, not the results, sometimes blatantly going against the direction implied by the data analysis (not so common in research papers),
- getting lucky/unlucky with subject performance, in a tiny sample, and claim certainty in the results.
Techniques used for analyzing basic performance measurements
The statistical design and analysis of experiments is a relatively recent invention (around 150 years old; verifying scientific hypotheses using experiments was first proposed over 1,000 years ago).
Once an experiment has been run, and performance measurements collected, what techniques are available to analyse the data?
Before electronic computers were invented, the practical statistical techniques were those that could be performed manually (perhaps with some help from a mechanical calculator).
Once computers became available, these manual use techniques were widely implemented in statistical applications and libraries. New statistical techniques have been invented that are only of practical when a computer is available, e.g., the bootstrap.
Most researchers in software engineering remain stuck in the pre-computer world of statistical analysis, i.e., failing to use more powerful techniques that make use of computers. Software engineering is not unique in being stuck using pre-computer statistical techniques, there are many other fields that have failed to move on to the more flexible and powerful techniques now available.
Performance comparison by benchmarking (i.e., running an experiment) is a common activity in scientific and engineering fields. Once the measurements have been made, what is the difference between pre-computer and post-manual statistical comparison techniques?
Performance comparison invariably involves comparing the mean/average of each set of measurements (one set for each product benchmarked). Random variations will have some impact on the measured values, and it’s possible that any difference in mean values is the result of these random variations. There are statistical tests for estimating the likelihood of the difference being due to random variation.
Statistical tests invariably come with preconditions on the characteristics of their input data, i.e., the test only works as advertised if the preconditions are met.
The t.test is a popular pre-computer method of estimating the likelihood that the difference between the means of two sets of measurements occurred by chance. Two of its preconditions are that the two sets of input data have a Normal/Gaussian distribution, and have the same standard deviation (if the standard deviations are not equal, Welch’s t-test should be used).
The Mann–Whitney U test (also known as the Wilcoxon rank-sum test) is a pre-computer method with a more relaxed precondition on the distribution of the inputs, requiring only that they are drawn from the same distribution (which need not be a Normal distribution; it is a non-parametric test). This test returns the likelihood of one group being less/greater than the other, and says nothing about the magnitude of the difference.
Removing the constraint that it must be practical to manually perform the calculations, led, in 1979, to a paper proposing the Bootstrap (major issues around the theory underpinning the bootstrap were answered by the early 1990s).
The Bootstrap, a post-manual method, does not have any preconditions on the distribution or standard deviation of the input data. An important precondition is that it is reasonable to assume that the elements of the two sets of measurements are exchangeable (more on this below).
The Bootstrap is a general technique that is not limited to only comparing mean values, it can be used to compare any quantity of interest (assuming the appropriate data is available).
The bootstrap algorithm starts by assuming that, if the two samples are combined into an aggregate sample, all possible permutations of values in this aggregate into two samples are equally likely (this is the exchangeability assumption). If this assumption is true, then any compared difference in the measured two samples will be roughly the same as the compared difference in a pair of random samples drawn from the aggregate.
The computational intensive component of a bootstrap test is generating many pairs of random samples (5,000 is a common choice; sampling with replacement, and saving the result of the comparison).
The comparison results of the paired random samples and the two measured samples are sorted. The position of the measured comparison in this sorted list is the test statistic, i.e., how extreme is the result from the measured samples, compared to the random samples?
News of the flexibility and power of the bootstrap are slowly permeating through the research community. There is an existing way of doing things, and there is little incentive to change. As Plank famously observed: “Science advances one funeral at a time.”
Learning General relativity at a rudimentary mathematical level
For the longest time, I have wanted to have an understanding of Einstein’s theory of General relativity at a rudimentary mathematical level. Because General relativity has never been a mainstream topic in undergraduate physics, there are almost no books at this level. Also, the mathematics of General relativity is based on tensor calculus, which until recently was rarely used in engineering and non-relativistic physics; market size explains the lack of non-specialist books on the subject.
The Theoretical Minimum is a book series that aims to teach everything required to gain a basic understanding of various areas of modern physics. The primary author of the books is Leonard Susskind.
At the start of this year, “General Relativity: The Theoretical Minimum” by Susskind and Cabannes was published as a paperback (i.e., convenient for reading on the London Underground), and over the last two months I have been slowly working my way through it.
At the start of this week, I discovered Eddie Boyes’ YouTube series on General relativity.
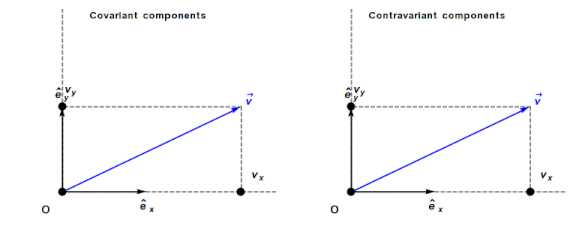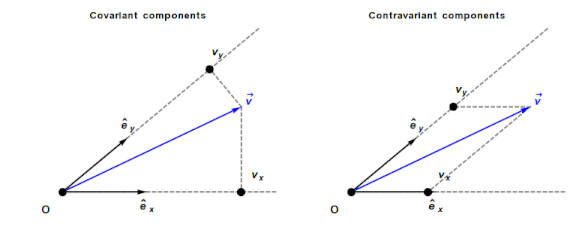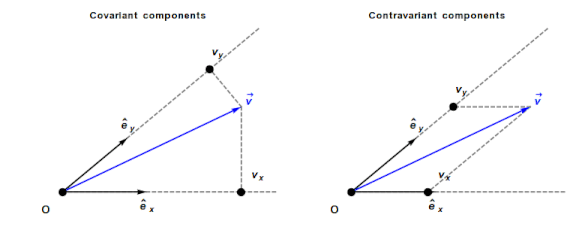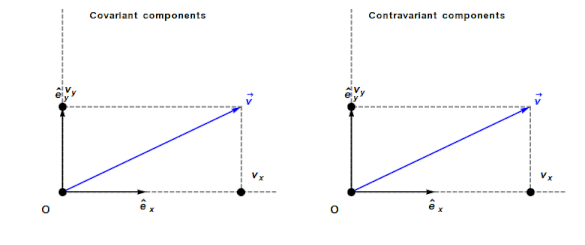
An understanding of General relativity requires an understanding of Tensor calculus, which in turn requires understanding the contravariant and covariant components of a vector. In the Cartesian coordinates system, which pervades undergraduate physics, the axes are at right angles and the measurement units are constant. The covariant component of a vector is the same as the contravariant component.
Contravariant/covariant vectors are different when the axes are not at right angles, as the plot below (from Wikipedia), shows. Choosing one component of the blue vector, the 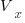 component of its contravariant vector is measured by drawing a line parallel to the y-axis (on right), while the
component of its contravariant vector is measured by drawing a line parallel to the y-axis (on right), while the 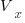 component of its covariant vector is found by drawing a line perpendicular to the x-axis (on left). The plot below shows how the measurements of each component vary as the angle between the x/y axes varies:
component of its covariant vector is found by drawing a line perpendicular to the x-axis (on left). The plot below shows how the measurements of each component vary as the angle between the x/y axes varies:
Susskind’s definition of covariant vectors is a differential equation, which might be enough for some people, but not me. Boyes gives a very clear description (he does labour points, and I watched at 1.75 speed).
There are other places where I found Boyes’ explanation to be clearer, and a few where I preferred Susskind. I would recommend both.
What complicates the use of Tensor calculus is the multiplicity of terms in an equation. In 3-dimensional Cartesian coordinates there are three variables x/y/z, while in 3-dimensional Tensor calculus there are nine variables (the coordinate system can produce an interaction between any axis and another one). The equation for the proper acceleration of an object, written using the Einstein summation convention (there is a summation over the repeated indexes, 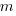 ,
,  ,
, 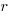 ) is:
) is: 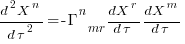 . In three dimensions, there would be three equations (i.e.,
. In three dimensions, there would be three equations (i.e., 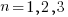 ), each with nine terms on the right, for
), each with nine terms on the right, for 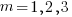 ,
, 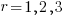 ;
; 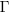 is the Christoffel symbol which calculates the unit distance for a location in space (in Cartesian coordinates this simplifies down to what we all learned in school); the superscripts denote contravariant components, and the subscripts denote covariant components:
is the Christoffel symbol which calculates the unit distance for a location in space (in Cartesian coordinates this simplifies down to what we all learned in school); the superscripts denote contravariant components, and the subscripts denote covariant components:
How did Einstein derive his field equation,  , of General relativity?
, of General relativity?
I had known of the equivalence principle, that the force experienced by an accelerating observer (e.g., travelling in an elevator) is indistinguishable from the force of gravity, but had not appreciated how this principle played an integral part in the derivation of the equations for the force experienced in a gravitational field.
The derivation is based on asking about the trajectory of a rocket accelerating at a constant rate in a flat space-time (allowing Cartesian coordinates to be used). If a stationary observer on the ground tracks the rocket from when it starts with zero velocity and then constantly accelerates in a straight line for a very long time, how will the velocity and distance of the rocket (from the observer) change over time? From the ground-based observer’s perspective, the rocket’s velocity will get closer and closer to the speed of light; Special relativity prevents it exceeding the speed of light. The distance travelled by the rocket over time, as tracked by the ground-based observer, will be seen to be fitted by a hyperbolic equation. This analysis is used to justify the use of hyperbolic geometric as a coordinate system for dealing with gravity.
A hyperbolic metric space was not enough for Einstein to derive his equations. He also assumed conservation of various quantities, and appears to have included some idealism about how the Universe ought to operate.
Special relativity predicts some very surprising behaviors, such as of time dilation. What very surprising behaviours does General relativity predict?
The bending of light by gravity is often cited as an example of a prediction by General relativity. However, bending is predicted my Newtonian mechanics, but the amount is half that predicted by General relativity.
While Black holes get a lot of public attention, and are discussion time by Susskind and Boyes, General relativity is not needed to make the prediction that that gravitational attraction of a sufficiently massive body will be greater than the speed of light.
General relativity deals with accelerating frames of reference (gravity or rocket ships). Both Susskind and Boyes discuss some version of Bell’s spaceship paradox, which is actually a consequence of Special relativity; I think that Boyes YouTube video is the easiest to follow.
Apart from ticking another item on my to-do list, I now appreciate some of the subtle points people make about General relativity. I’m sure that this knowledge will increase the likelihood of me getting in over my head in some future discussion on relativity.
Distribution of program sizes
Program size, in lines of code (LOC), used to be a topic of conversation among developers and managers. Program size is an issue when computer memory is measured in kilobytes. Large programs would be organized into overlays such that only small subsets needed to be held in memory at any time, i.e., programmer defined memory management.
Management used program size as a proxy for implementation effort/cost. Because size was a topic of conversation, it was possible to ask around to obtain a selection of values for the size of programs with similar functionality (accurate actual implementation costs were/are rarely available via the grapevine, but developers were/are always happy to talk about how small/large their programs were/are). These days, estimating LOC prior to implementation may appear more scientific, but I doubt it’s more accurate.
Once computers containing megabytes of memory became widespread, and the use of third-party libraries continued to grow, program size became a niche topic of conversation.
The size of some operating systems has become an occasional topic of conversation; it wasn’t previously because mainframe/mini computer manufacturers didn’t want customers talking about how much of their expensive memory was taken up by the OS. The size of Microsoft Windows leaked out and the Linux kernel is a topic of research.
Discussions around size have moved on from individual programs to the amount of space taken up by an installed application suite. Today, program size can be a rounding error compared to data files, extensions and add-ons.
Researchers have also moved on; repository size, in LOC/packages, is what now gets reported.
For those who are interested in program size; what is the distribution of program sizes? How many LOC are needed for a program to be above 50%, or in the top 95%?
Recent data on the size of individual programs is surprisingly hard to find, given how often LOC values appear in print. The one dataset I found is from the paper Empirical analysis of the relationship between CC and SLOC in a large corpus of Java methods and C functions, which is derived from the 2010’ish Sourcerer corpus of 13,103 Java projects (each of which I assume contains one program). The plot below shows the LOC (red) and methods (blue/green) for each program, in ascending order, along with values at various percentage points (code+data):
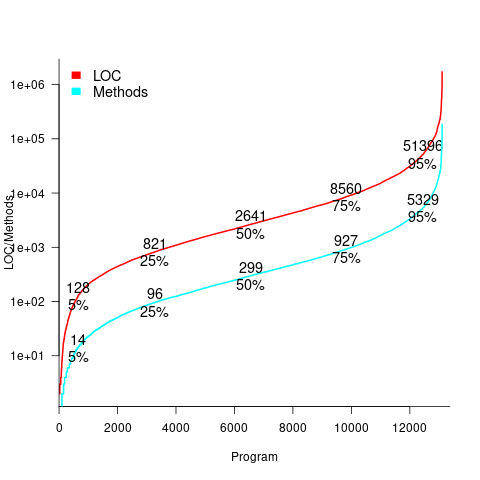
The size of Java programs is very likely to have increased since 2010. How much have grown? I don’t know.
What about the size of programs written in other languages?
I expect Python program size to be smaller, because the huge number of available package removes the need to implement a myriad of boilerplate functionality.
I expect C program size to be larger, both because of the smaller library ecosystem and because C programs tend to be older (programs rarely shrink with age).
Recent Comments