Archive
Remotivating data analysed for another purpose
The motivation for fitting a regression model has a major impact on the model created. Some of the motivations include:
- practicing software developers/managers wanting to use information from previous work to help solve a current problem,
- researchers wanting to get their work published seeks to build a regression model that show they have discovered something worthy of publication,
- recent graduates looking to apply what they have learned to some data they have acquired,
- researchers wanting to understand the processes that produced the data, e.g., the author of this blog.
The analysis in the paper: An Empirical Study on Software Test Effort Estimation for Defense Projects by E. Cibir and T. E. Ayyildiz, provides a good example of how different motivations can produce different regression models. Note: I don’t know and have not been in contact with the authors of this paper.
I often remotivate data from a research paper. Most of the data in my Evidence-based Software Engineering book is remotivated. What a remotivation often lacks is access to the original developers/managers (this is often also true for the authors of the original paper). A complicated looking situation is often simplified by background knowledge that never got written down.
The following table shows the data appearing in the paper, which came from 15 projects implemented by a defense industry company certified at CMMI Level-3.
Proj Test Req Test Meetings Faulty Actual Scenarios
Plan Rev Env Scenarios Effort
Time Time
P1 144.5 1.006 85 60 100 2850 270
P2 25.5 1.001 25.5 4 5 250 40
P3 68 1.005 42.5 32 65 1966 185
P4 85 1.002 85 104 150 3750 195
P5 198 1.007 123 87 110 3854 410
P6 57 1.006 35 25 20 903 100
P7 115 1.003 92 55 56 2143 225
P8 81 1.009 156 62 72 1988 287
P9 388 1.004 150 208 553 13246 1153
P10 177 1.008 93 77 157 4012 360
P11 62 1.001 175 186 199 5017 310
P12 111 1.005 116 82 143 3994 423
P13 63 1.009 188 177 151 3914 226
P14 32 1.008 25 28 6 435 63
P15 167 1.001 177 143 510 11555 1133 |
where: TestPlanTime is the test plan creation time in hours, ReqRev is the test/requirements review of period in hours, TestEnvTime is the test environment creation time in hours, Meetings is the number of meetings, FaultyScenarios is the number of faulty test scenarios, Scenarios is the number of Scenarios, and ActualEffort is the actual software test effort.
Industrial data is hard to obtain, so well done to the authors for obtaining this data and making it public. The authors fitted a regression model to estimate software test effort, and the model that almost perfectly fits to actual effort is:
ActualEffort=3190 + 2.65*TestPlanTime
-3170*ReqRevPeriod - 3.5*TestEnvTime
+10.6*Meetings + 11.6*FaultScrenarios + 3.6*Scenarios |
My reading of this model is that having obtained the data, the authors felt the need to use all of it. I have been there and done that.
Why all those multiplication factors, you ask. Isn’t ActualTime simply the sum of all the work done? Yes it is, but the above table lists the work recorded, not the work done. The good news is that the fitted regression models shows that there is a very high correlation between the work done and the work recorded.
Is there a simpler model that can be used to explain/predict actual time?
Looking at the range of values in each column, ReqRev varies by just under 1%. Fitting a model that does not include this variable, we get (a slightly less perfect fit):
ActualEffort=100 + 2.0*TestPlanTime
- 4.3*TestEnvTime
+10.7*Meetings + 12.4*FaultScrenarios + 3.5*Scenarios |
Simple plots can often highlight patterns present in a dataset. The plot below shows every column plotted against every other column (code+data):

Points forming a straight line indicate a strong correlation, and the points in the top-right ActualEffort/FaultScrenarios plot look straight. In fact, this one variable dominates the others, and fits a model that explains over 99% of the deviation in the data:
ActualEffort=550 + 22.5*FaultScrenarios |
Many of the points in the ActualEffort/Screnarios plot are on a line, and adding Meetings data to the model explains just under 99% of the variance in the data:
actualEffort=-529.5
+15.6*Meetings + 8.7*Scenarios |
Given that FaultScrenarios is a subset of Screnarios, this connectedness is not surprising. Does the number of meetings correlate with the number of new FaultScrenarios that are discovered? Questions like this can only be answered by the original developers/managers.
The original data/analysis was interesting enough to get a paper published. Is it of interest to practicing software developers/managers?
In a small company, those involved are likely to already know what these fitted models are telling them. In a large company, the left hand does not always know what the right hand is doing. A CMMI Level-3 certified defense company is unlikely to be small, so this analysis may be of interest to some of its developer/managers.
A usable estimation model is one that only relies on information available when the estimation is needed. The above models all rely on information that only becomes available, with any accuracy, way after the estimate is needed. As such, they are not practical prediction models.
Putnam’s software equation debunked
The implementation of a project has a lifecycle that starts and finishes with zero people working on it. Between starting and finishing, the number of staff quickly grows to a peak before slowly declining. In a series of very hard to obtain papers during the early 1960s (chapter 5), Peter Norden created a large project staffing model described by the Rayleigh equation. This model was evangelized by Lawrence Putnam in the 1970s, who called it the Norden/Rayleigh model, while others sometimes now call it the Norden/Putnam, Putnam/Rayleigh, or some combination of names; Putnam’s papers can be hard to obtain.
The Norden/Rayleigh equation is: 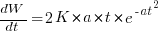
where: 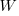 is work completed,
is work completed, 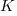 is total manpower over the lifespan of the project,
is total manpower over the lifespan of the project, 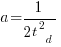 ,
, 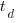 is time of maximum effort per unit time (i.e., the Norden/Rayleigh equation maximum value, which Putnam calls project development time), and
is time of maximum effort per unit time (i.e., the Norden/Rayleigh equation maximum value, which Putnam calls project development time), and 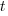 is project elapsed time.
is project elapsed time.
Norden’s model is only applicable to large projects (e.g., 2+ man-years), and Putnam points out that the staffing of small projects is usually a square wave, i.e., a number of staff are allocated at the start and this number remains the same until project completion.
As well as evangelizing Norden’s model, Putnam also created his own model; an equation connecting delivered lines of code, total manpower and project duration. The usually cited paper for this work is: “A General Empirical Solution to the Macro Software Sizing and Estimating Problem”, which can sometimes be found as a free download. I had always assumed that people did not take this model seriously, and it was not worth my time debunking it. The paper makes conjures hand-wavy connections between various equations which don’t seem to go anywhere, and eventually connects together a regression equation fitted to nine data points with an observation+assumption about another regression equation to create what Putnam calls the software equation: 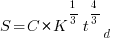 , where
, where 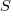 is delivered source code statements, and
is delivered source code statements, and 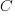 is a constant.
is a constant.
I recently read a 2014 paper by Han Suelmann debunking Putnam’s software equation, which led me to question my assumption about people not using Putnam’s model. Google Scholar shows 1,411 citations, with 133 since 2020. It looks like the software equation is still being taken seriously (or researchers are citing it because everybody else does; a common practice).
Why isn’t Putnam’s software equation worth treating seriously?
First, Putnam’s derivation of the software equation reads like a just-so story based on a tiny amount of data, and second a larger independent dataset does not show the pattern seen in Putnam’s data.
The derivation of the software equation starts by defining productivity as the number of delivered source code statements divided by the total manpower consumed to produce them, 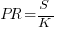 . Ok.
. Ok.
There is more certainty to a line fitted to a set of points that roughly follow a straight line, than to fit a line to points that follow a curve (because there are usually many ‘curve’ equations to choose from). The Norden/Rayleigh equation can be transformed to a form that is amenable to fitting a straight line, i.e., dividing by time and taking logs, as follows (which plugs in the value of 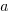 ):
):
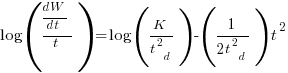
Putnam noticed (or perhaps it was the authors of the cited prepublication paper “Software budgeting model” by G. E. P. Box and L. Pallesen, which I cannot locate a copy of) that when plotting 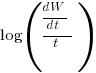 against
against 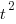 : “If the number
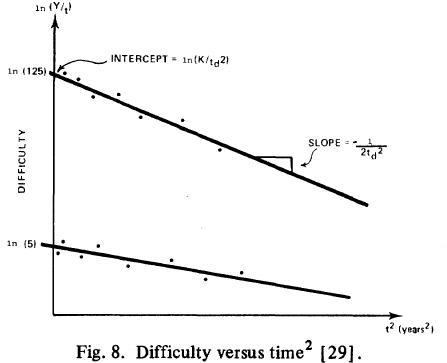
: “If the number 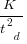 was small, it corresponded with easy systems; if the number was large, it corresponded with hard systems and appeared to fall in a range between these extremes.” Notice that in the screenshot of a figure from Putnam’s paper below, the y-axis is labelled “Difficulty”, not with the quantity actually plotted.
was small, it corresponded with easy systems; if the number was large, it corresponded with hard systems and appeared to fall in a range between these extremes.” Notice that in the screenshot of a figure from Putnam’s paper below, the y-axis is labelled “Difficulty”, not with the quantity actually plotted.
Based on an observation about easy/hard systems (it is never explained how easy/hard is measured) something called difficulty is defined to be: 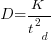 . No explanation is given for dropping the log scaling, or the possibility that some other relationship might hold.
. No explanation is given for dropping the log scaling, or the possibility that some other relationship might hold.
The screenshot below is of a figure from Putnam’s paper, which plots the values of 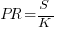 against
against 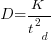 for 13 projects. The fitted regression lines (the three lines are fitted using, 9, 2 and 2 points of the 13 projects) have the form
for 13 projects. The fitted regression lines (the three lines are fitted using, 9, 2 and 2 points of the 13 projects) have the form 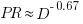 , i.e.,
, i.e., 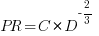 (I extracted the points and fitted
(I extracted the points and fitted 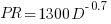 ; code+extracted data):
; code+extracted data):
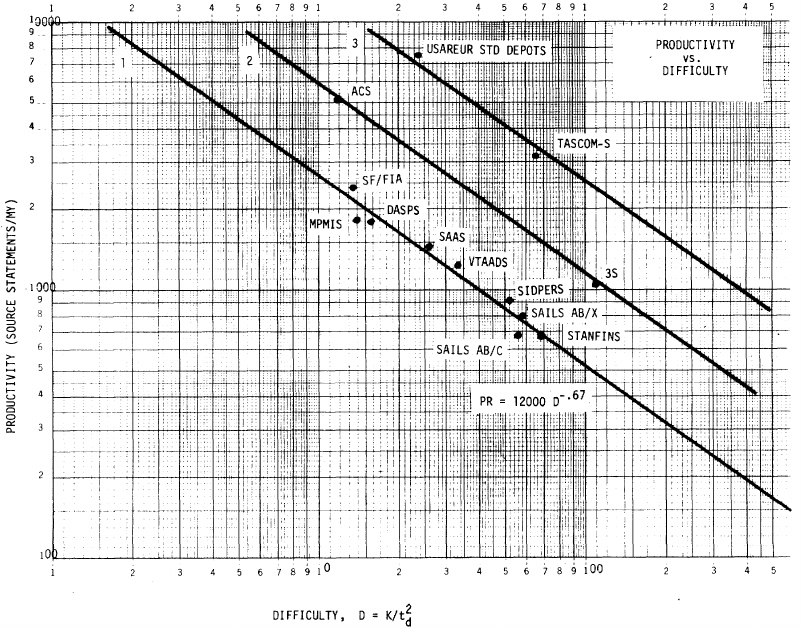
With a bit of algebra, the two equations: 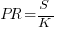 and
and 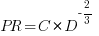 , can be combined to create the software equation.
, can be combined to create the software equation.
Yes, Putnam’s software equation was hand-waved into existence by plucking a “difficulty” component from an observation about the behavior of projects in a regression model and equating it to a regression line fitted to nine points.
Are the patterns seen by Putnam found in other projects?
In the 1987 paper “Time-Sensitive Cost Models in the Commercial MIS Environment” D. Ross Jeffery used data from 47 projects to investigate the effort/time relationships used by Putnam to derive his software equation.
The plot below, of log(Difficulty) vs log(Productivity), shows what appears to be a random scattering of points, confirmed by failing to fit a regression model (code+extracted data):
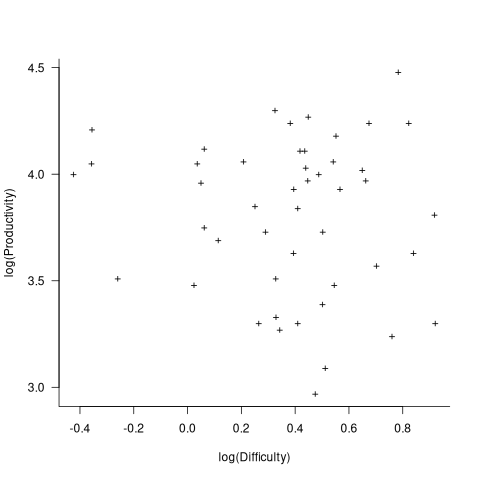
No. The patterns seen by Putnam are not present in these projects. I don’t think that the difference in application domain is relevant (Putnam’s projects were for Military systems and Jeffery’s are for commercial projects). Norden’s model is not specific to software projects.
Jeffery’s uses a regression model to find: 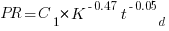 , the corresponding Putnam equation is:
, the corresponding Putnam equation is: 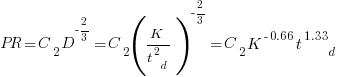 (the paper does not include the plot needed to extract the required data). The
(the paper does not include the plot needed to extract the required data). The 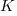 exponent might be claimed to be close enough, but the
exponent might be claimed to be close enough, but the 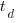 exponent is very different.
exponent is very different.
Jeffery’s paper includes a plot of 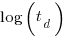 against
against 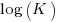 , and the plot below shows the extracted data (44 points), plus fitted regression line (code+extracted data):
, and the plot below shows the extracted data (44 points), plus fitted regression line (code+extracted data):
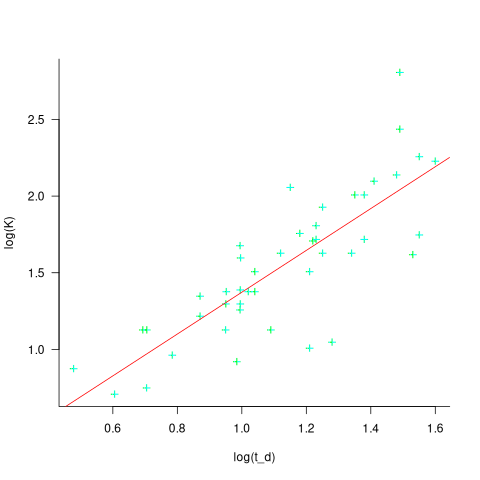
The regression line has the form 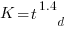 . This relationship further undermines assumptions made by Putnam, e.g., smaller systems are easier.
. This relationship further undermines assumptions made by Putnam, e.g., smaller systems are easier.
The Han Suelmann paper that triggered this post takes a very different approach to debunking Putnam’s model (he uses simulation to show that random data, drawn from a suitable distribution, can produce the patterns seen by Putnam).
Modelling estimate/actual including uncertainty in the estimate
What is an effective technique for modelling the relationship between the time estimated to implement a task and the actual time taken to implement that task?
A regression model is the obvious approach. However, an important assumption made by the commonly used regression techniques is not met by estimate/actual project data
The commonly used regression techniques involve two kinds of variables: the explanatory variable and the response variable (also known as the independent and dependent variables). For instance, in the equation 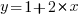 ,
,  is the explanatory variable and
is the explanatory variable and 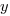 is the response variable.
is the response variable.
When fitting a regression model to measurement data, the fitted equation is assumed to have the form such as: 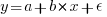 , where
, where 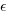 is uncertainty in the value of
is uncertainty in the value of 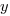 , with the
, with the  valued assumed to have no uncertainty;
valued assumed to have no uncertainty; 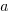 and
and 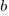 are constants fitted by the modelling process. The values returned by the model fitting process include an estimate for
are constants fitted by the modelling process. The values returned by the model fitting process include an estimate for 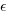 , as well as estimates for
, as well as estimates for 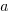 and
and 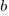 .
.
When running an experiment, the values of the explanatory variables(e.g.,  ) are chosen by the experimenter, with the subject providing the value of the response variable, e.g.,
) are chosen by the experimenter, with the subject providing the value of the response variable, e.g., 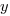 .
.
What does this technical detail have to do with estimation data?
The task estimate/actual values are both provide by the subject (i.e., the developer), there is no experimenter providing one of the values; in fact there is no experiment, these are measurements of things that happened. Both the estimate and actual are response variables, and both contain some amount of uncertainty, and the fitting process needs to take this into account. The appropriate regression technique to use for this case is an errors-in-variables model, which fits the equation  , with
, with  being the uncertainty in
being the uncertainty in  .
.
A previous post discussed the surprising behavior that can occur when failing to use errors-in-variables regression for where the data does not contain any explanatory variables, i.e., all the variables contain uncertainty.
The process of fitting an errors-in-variables regression model requires additional input, a value for  has to be specified. Taking the example of task estimation, possible uncertainties in the estimate include: misunderstanding of the requirement(s), faded memory of the actual time previously taken by very similar tasks, an inaccurate model of developer skills, and a preference for using round numbers.
has to be specified. Taking the example of task estimation, possible uncertainties in the estimate include: misunderstanding of the requirement(s), faded memory of the actual time previously taken by very similar tasks, an inaccurate model of developer skills, and a preference for using round numbers.
What data is available on the uncertainty of individual task estimates? I know of one study where, unknown to them, the individuals estimated the same task twice (in fact, seven people each estimated the same six distinct tasks twice, over a period of three-months). The plot below shows the first/second estimate made by each person for each of the six tasks, with the grey line showing where first==second estimate (code+data):
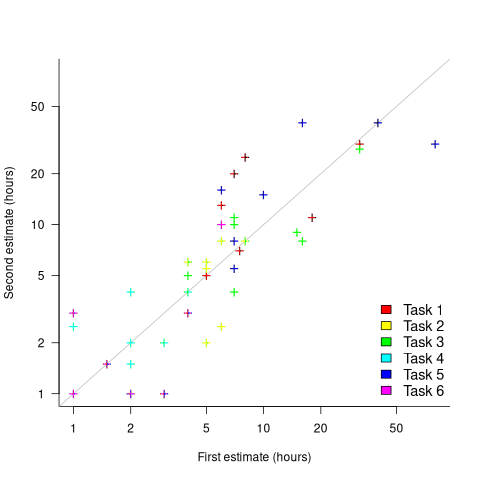
Assuming the estimation uncertainty in this experiment’s data is roughly equal to the estimation uncertainty in other estimation datasets, of tasks taking up to 20 hours, how might it be used to calculate a value for the uncertainty in estimated values?
Two possibilities include:
- Assuming that the uncertainty in both the first and second estimates is equal, a model can be fitted using Deming regression (which treats both variables as having the same uncertainty), and the residual standard error of this model used as the value of
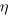 . This value for a fitted multiplicative model is 0.6 (code+data),
. This value for a fitted multiplicative model is 0.6 (code+data), - using the mean of the relative errors,
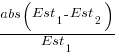 ; its value is 0.55.
; its value is 0.55.
How different are the models built using linear regression and errors-in-variables regression, for small task estimates?
A basic linear regression model fitted to the SiP estimation dataset is: 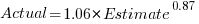 .
.
Updating this model, using SIMEX, to take into uncertainty in the value of 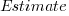 gives, for an uncertainty error of 0.55:
gives, for an uncertainty error of 0.55: 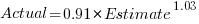 , and for an uncertainty error of 0.60:
, and for an uncertainty error of 0.60: 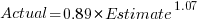 . The coefficients for the two models are essentially the same (code+data).
. The coefficients for the two models are essentially the same (code+data).
The exponent value is the noticeable difference between the linear regression and errors-in-variables regression models. Adding the assumed amount of uncertainty (based on data from one experiment) to the estimated value leads to a model where estimate/actual are very close to having a linear relationship.
Is this errors-in-variables model any closer to reality than the linear regression model? The model shows that the estimate/actual relationship is closer to linear than was previously thought. Until more data becomes available, we won’t know how close this relationship actually is.
The people who made the estimates in the SiP data also performed the work that took the recorded actual time. Assigning a task to a different person could produce both a different estimate and a different actual, but these possible values are unknown. On a larger scale, different companies bidding on the same contract specify different amounts and have different implementations times; data showing these differences.
A surprising retrospective task estimation dataset
When estimating the time needed to implement a task, the time previously needed to implement similar tasks provides useful guidance. The implementation time for these previous tasks may itself be estimated, because the actual time was not measured or this information is currently unavailable.
How accurate are developer time estimates of previously completed tasks?
I am not aware of any software related dataset of estimates of previously completed tasks (it’s hard enough finding datasets containing information on the actual implementation time). However, I recently found the paper Dynamics of retrospective timing: A big data approach by Balcı, Ünübol, Grondin, Sayar, van Wassenhove, and Wittmann. The data analysed comes from a survey questionnaire, where 24,494 people estimated the how much time they had spent answering the questions, along with recording the current time at the start/end of the questionnaire. The supplementary data is in MATLAB format, and is also available as a csv file in the Blursday database (i.e., RT_Datasets).
Some of the behavior patterns seen in software engineering estimates appear to be general human characteristics, e.g., use of round numbers. An analysis of the estimation performance of a wide sample of the general population could help separate out characteristics that are specific to software engineering and those that apply to the general population.
The following table shows the percentage of answers giving a particular Estimate and Actual time, in minutes. Over 60% of the estimates are round numbers. Actual times are likely to be round numbers because people often give a round number when asked the time (code+data):
Minutes Estimate Actual
20 18% 8.5%
15 15% 5.3%
30 12% 7.6%
25 10% 6.2%
10 7.7% 2.1% |
I was surprised to see that the authors had fitted a regression model with the Actual time as the explanatory variable and the Estimate as the response variable. The estimation models I have fitted always have the roles of these two variables reversed. More of this role reversal difference below.
The equation fitted to the data by the authors is (they use the term Elapsed, for consistency with other blog articles I continue to use Actual; code+data):
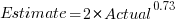
This equation says that, on average, for shorter Actual times the Estimate is higher than the Actual, while for longer Actual times the average Estimate is lower.
Switching the roles of the variables, I expected to see a fitted model whose coefficients are somewhat similar to the algebraically transformed version of this equation, i.e., 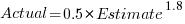 . At the very least, I expected the exponent to be greater than one.
. At the very least, I expected the exponent to be greater than one.
Surprisingly, the equation fitted with the variables roles reversed is very similar, i.e., the equations are the opposite of each other:
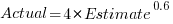
This equation says that, on average, for shorter Estimate times the Actual time is higher than the Estimate, while for longer Estimate times the average Actual is lower, i.e., the opposite behavior specifie dby the earlier equation.
I spent some time trying to understand how it was possible for data to be fitted such that (x ~ y) == (y ~ x), even posting a question to Cross Validated. I might, in a future post, discuss the statistical issues behind this behavior.
So why did the authors of this paper treat Actual as an explanatory variable?
After a flurry of emails with the lead author, Fuat Balcı (who was very responsive to my questions), where we both doubled checked the code/data and what we thought was going on, Fuat answered that (quoted with permission):
“The objective duration is the elapsed time (noted by the experimenter based on a clock reading), and the estimate is the participant’s response. According to the psychophysical approach the mapping between objective and subjective time can be defined by regressing the subjective estimates of the participants on the objective duration noted by the experimenter. Thus, if your research question is how human’s retrospective experience of time changes with the duration of events (e.g., biases in time judgments), the y-axis should be the participant’s response and the x-axis should be the actual duration.”
This approach has a logic to it, and is consistent with the regression modelling done by other researchers who study retrospective time estimation.
So which modelling approach is correct, and are people overestimating or underestimating shorter actual time durations?
Going back to basics, the structure of this experiment does not produce data that meets one of the requirements of the statistical technique we are both using (ordinary least squares) to fit a regression model. To understand why ordinary least squares, OLS, is not applicable to this data, it’s necessary to delve into a technical detail about the mathematics of what OLS does.
The equation actually fitted by OLS is:  , where
, where  is an error term (i.e., ‘noise’ caused by all the effects other than
is an error term (i.e., ‘noise’ caused by all the effects other than  ). The value of
). The value of  is assumed to be exact, i.e., not contain any ‘noise’.
is assumed to be exact, i.e., not contain any ‘noise’.
Usually, in a retrospective time estimation experiment, subjects hear, for instance, a sound whose duration is decided in advance by the experimenter; subjects estimate how long each sound lasted. In this experimental format, it makes sense for the Actual time to appear on the right-hand-side as an explanatory variable and for the Estimate response variable on the left-hand-side.
However, for the questionnaire timing data, both the Estimate and Actual time are decided by the person giving the answers. There is no experimenter controlling one of the values. Both the Estimate and Actual values contain ‘noise’. For instance, on a different day a person may have taken more/less time to actually answer the questionnaire, or provided a different estimate of the time taken.
The correct regression fitting technique to use is errors-in-variables. An errors-in-variables regression fits the equation: 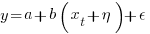 , where:
, where: 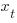 is the true value of
is the true value of  and
and 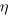 is its associated error. A selection of packages are available for fitting a variety of errors-in-variables models.
is its associated error. A selection of packages are available for fitting a variety of errors-in-variables models.
I regularly see OLS used in software engineering papers (including mine) where errors-in-variables is the technically correct technique to use. Researchers are either unaware of the error issues or assuming that the difference is not important. The few times I have fitted an errors-in-variables model, the fitted coefficients have not been much different from those fitted by an OLS model; for this dataset the coefficient difference is obviously important.
The complication with building an errors-in-variables model is that values need to be specified for the error terms 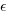 and
and 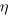 . With OLS the value of
. With OLS the value of 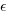 is produced as part of the fitting process.
is produced as part of the fitting process.
How might the required error values be calculated?
If some subjects round reported start/stop times, there may not be any variation in reported Actual time, or it may jump around in 5-minute increments depending on the position of the minute hand on the clock.
Learning researchers have run experiments where each subject performs the same task multiple times. Performance improves with practice, which makes it difficult to calculate the likely variability in the first-time performance. If we assume that performance is skill based, the standard deviation of all the subjects completing within a given timeframe could be used to calculate an error term.
With 60% of Estimates being round numbers, there might not be any variation for many people, or perhaps the answer given will change to a different round number. There is Estimate data for different, future tasks, and a small amount of data for the same future tasks. There is data from many retrospective studies using very short time intervals (e.g., tens of seconds), which might be applicable.
We could simply assume that the same amount of error is present in each variable. Deming regression is an errors-in-variables technique that supports this approach, and does not require any error values to be specified. The following equations have been fitted using Deming regression (code+data):
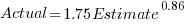
and
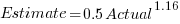
While these two equations are consistent with each other, we don’t know if the assumption of equal errors in both variables is realistic.
What next?
Hopefully it will be possible to work out reasonable error values for the Actual/Estimate times. Fitting a model using these values will tell us wether any over/underestimating is occurring, and the associated span of time durations.
I also need to revisit the analysis of software task estimation times.
What is known about software effort estimation in 2024
It’s three years since my 2021 post summarizing what I knew about estimating software tasks. While no major new public datasets have appeared (there have been smaller finds), I have talked to lots of developers/managers about the findings from the 2019/2021 data avalanche, and some data dots have been connected.
A common response from managers, when I outline the patterns found, is some variation of: “That sounds about right.” While it’s great to have this confirmation, it’s disappointing to be telling people what they already know, even if I can put numbers to the patterns.
Some of the developer behavior patterns look, to me, to be actionable, e.g., send developers on a course to unbias their estimates. In practice, managers are worried about upsetting developers or destabilising teams. It’s easy for an unhappy developer to find another job (the speakers at the meetups I attend often end by saying: “and we’re hiring.”)
This post summarizes a talk I gave recently on what is known about software estimating; a video will eventually appear on the British Computer Society‘s Software Practice Advancement group’s YouTube channel, and the slides are on Github.
What I call the historical estimation models contain source code, measured in lines, as a substantial component, e.g., COCOMO which overfits a miniscule dataset. The problem with this approach is that estimates of the LOC needed to implement some functionality LOC are very inaccurate, and different developers use different LOC to implement the same functionality.
Most academic research in software effort estimation continues to be based on miniscule datasets; it’s essentially fake research. Who is doing good research in software estimating? One person: Magne Jørgensen.
Almost all the short internal task estimate/actual datasets contain all the following patterns:
- use of round-numbers (known as heaping in some fields). The ratios of the most frequently used round numbers, when estimating time, are close to the ratios of the Fibonacci sequence,
- short tasks tend to be under-estimated and long tasks over-estimate. Surprisingly, the following equation is a good fit for many time-based datasets:
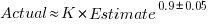 ,
, - individuals tend to either consistently over or under estimate (this appears to be connected with the individual’s risk profile),
- around 30% of estimates are accurate, 68% within a factor of two, and 95% within a factor of four; one function point dataset, one story point dataset, many time datasets,
- developer estimation accuracy does not change with practice. Possible reasons for this include: variability in the world prevents more accurate estimates, developers choose to spend their learning resources on other topics (such as learning more about the application domain).
I have a new ChatGPT generated image for my slide covering the #Noestimates movement:

Estimation accuracy in the (building|road) construction industry
Lots of people complain about software development taking longer than estimated. Are estimates in other industries more accurate, and do they contain patterns similar to those seen in software task estimates?
Readers will probably not be surprised to learn that obtaining estimate/actual data is as hard for other industries as it is for software.
Software engineering sometimes gets compared with building construction, in the sense that building construction is perceived as being straightforward and predictable. My tiny experience with building construction is that it is not as straightforward and predictable as outsiders think, a view echoed by the few people in the building industry I have spoken to.
I have found two building datasets, the supplementary material from: Forecasting the Project Duration Average and Standard Deviation from Deterministic Schedule Information (the 101 rows also include some service projects), and Ballesteros-Pérez kindly sent me the data for Duration and Cost Variability of Construction Activities: An Empirical Study which included 746 rows of road construction estimate/actual data from an unknown source. This data is for large projects, where those involved had to bid to get the work.
The following plot reminds us of how effort vs actual often looks like for short software tasks; it includes a fitted regression model and prediction intervals at one standard deviation (68.3%) and two standard deviations (95%); the faint grey line shows Estimate == Actual (post discussing the analysis and linking to code+data):
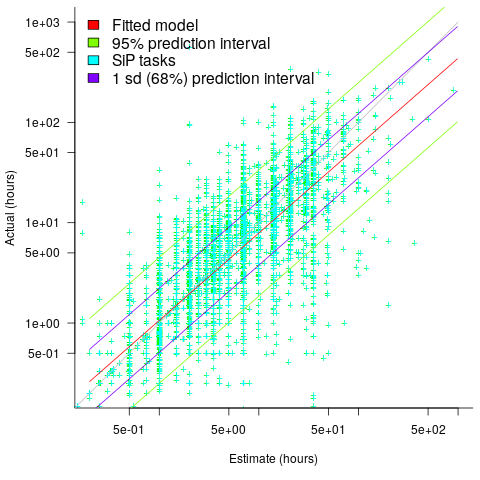
The data in the above plot is for small tasks, which did not involve bidding for the work.
The following plot shows estimated vs actual duration for 101 construction projects. The red line has the form: 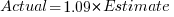 , i.e., average estimate is 9% lower than actual duration (blue line shows
, i.e., average estimate is 9% lower than actual duration (blue line shows 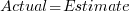 ; code+data).
; code+data).
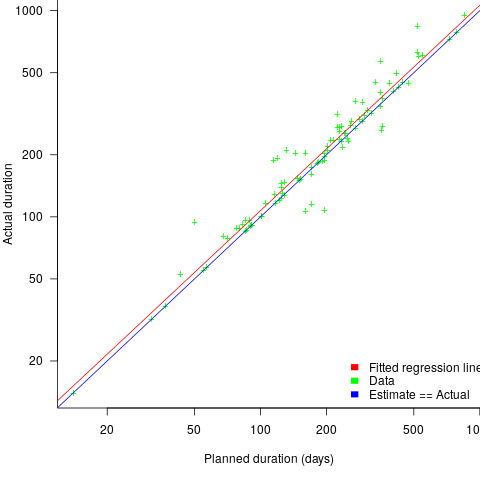
The obvious differences are that the fitted line shows consistent underestimation (hardly surprising when bidding for work; 16% of estimates are greater than the actual), that the variance of project estimate/actual about the line is much smaller for building construction, and that the red/blue lines are essentially parallel (the exponent for software tasks is consistently around 0.85, rather than 1)
The following plot shows estimated vs actual for 746 road construction projects. The red line has the form: 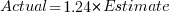 , i.e., average estimate is 24% lower than actual duration (blue line shows
, i.e., average estimate is 24% lower than actual duration (blue line shows 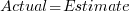 ; code+data):
; code+data):
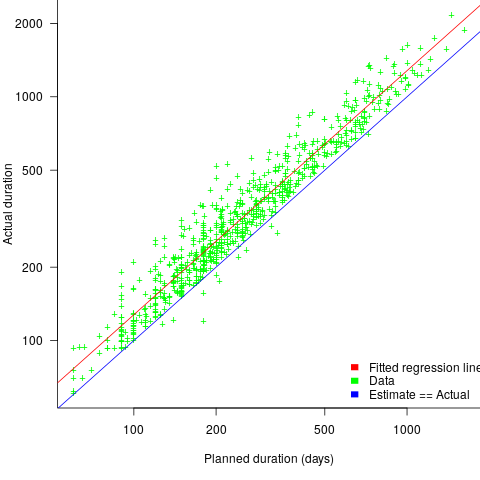
Again there is a consistent average underestimate (project bidding was via an auction process), the red/blue lines are essentially parallel, and while the estimate/actual variance is larger than for building construction only 1.5% estimates are greater than the actual.
Consistent underestimating is not surprising for external projects awarded via a bidding process.
The unpredicted differences are the much smaller estimate/actual variance (compared to software), and the fitted line running parallel to 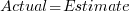 .
.
Estimating quantities from several hundred to several thousand
How much influence do anchoring and financial incentives have on estimation accuracy?
Anchoring is a cognitive bias which occurs when a decision is influenced by irrelevant information. For instance, a study by John Horton asked 196 subjects to estimate the number of dots in a displayed image, but before providing their estimate subjects had to specify whether they thought the number of dots was higher/lower than a number also displayed on-screen (this was randomly generated for each subject).
How many dots do you estimate appear in the plot below?

Estimates are often round numbers, and 46% of dot estimates had the form of a round number. The plot below shows the anchor value seen by each subject and their corresponding estimate of the number of dots (the image always contained five hundred dots, like the one above), with round number estimates in same color rows (e.g., 250, 300, 500, 600; code+data):
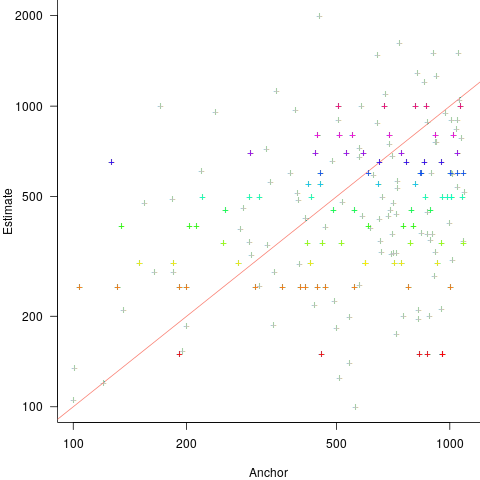
How much influence does the anchor value have on the estimated number of dots?
One way of measuring the anchor’s influence is to model the estimate based on the anchor value. The fitted regression equation 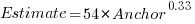 explains 11% of the variance in the data. If the higher/lower choice is included the model, 44% of the variance is explained; higher equation is:
explains 11% of the variance in the data. If the higher/lower choice is included the model, 44% of the variance is explained; higher equation is: 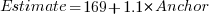 and lower equation is:
and lower equation is: 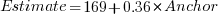 (a multiplicative model has a similar goodness of fit), i.e., the anchor has three-times the impact when it is thought to be an underestimate.
(a multiplicative model has a similar goodness of fit), i.e., the anchor has three-times the impact when it is thought to be an underestimate.
How much would estimation accuracy improve if subjects’ were given the option of being rewarded for more accurate answers, and no anchor is present?
A second experiment offered subjects the choice of either an unconditional payment of $2.50 or a payment of $5.00 if their answer was in the top 50% of estimates made (labelled as the risk condition).
The 196 subjects saw up to seven images (65 only saw one), with the number of dots varying from 310 to 8,200. The plot below shows actual number of dots against estimated dots, for all subjects; blue/green line shows 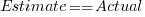 , and red line shows the fitted regression model
, and red line shows the fitted regression model 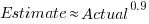 (code+data):
(code+data):
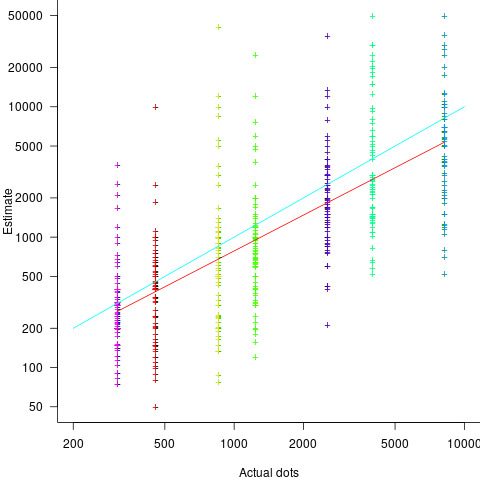
The variance in the estimated number of dots is very high and increases with increasing actual dot count, however, this behavior is consistent with the increasing variance seen for images containing under 100 dots.
Estimates were not more accurate in those cases where subjects chose the risk payment option. This is not surprising, performance improvements require feedback, and subjects were not given any feedback on the accuracy of their estimates.
Of the 86 subjects estimating dots in three or more images, 44% always estimated low and 16% always high. Subjects always estimating low/high also occurs in software task estimates.
Estimation patterns previously discussed on this blog have involved estimated values below 100. This post has investigated patterns in estimates ranging from several hundred to several thousand. Patterns seen include extensive use of round numbers and increasing estimate variance with increasing actual value; all seen in previous posts.
NoEstimates panders to mismanagement and developer insecurity
Why do so few software development teams regularly attempt to estimate the duration of the feature/task/functionality they are going to implement?
Developers hate giving estimates; estimating is very hard and estimates are often inaccurate (at a minimum making the estimator feel uncomfortable and worse when management treats an estimate as a quotation). The future is uncertain and estimating provides guidance.
Managers tell me that the fear of losing good developers dissuades them from requiring teams to make estimates. Developers have told them that they would leave a company that required them to regularly make estimates.
For most of the last 70 years, demand for software developers has outstripped supply. Consequently, management has to pay a lot more attention to the views of software developers than the views of those employed in most other roles (at least if they want to keep the good developers, i.e., those who will have no problem finding another job).
It is not difficult for developers to get a general idea of how their salary, working conditions and practices compares with other developers in their field/geographic region. They know that estimating is not a common practice, and unless the economy is in recession, finding a new job that does not require estimation could be straight forward.
Management’s demands for estimates has led to the creation of various methods for calculating proxy estimate values, none of which using time as the unit of measure, e.g., Function points and Story points. These methods break the requirements down into smaller units, and subcomponents from these units are used to calculate a value, e.g., the Function point calculation includes items such as number of user inputs and outputs, and number of files.
How accurate are these proxy values, compared to time estimates?
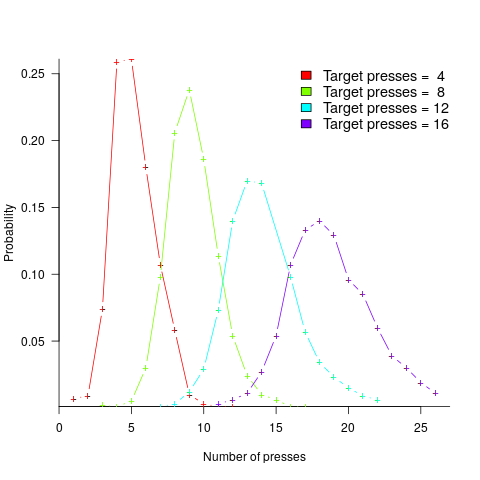
As always, software engineering data is sparse. One analysis of 149 projects found that 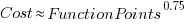 , with the variance being similar to that found when time was estimated. An analysis of Function point calculation data found a high degree of consistency in the calculations made by different people (various Function point organizations have certification schemes that require some degree of proficiency to pass).
, with the variance being similar to that found when time was estimated. An analysis of Function point calculation data found a high degree of consistency in the calculations made by different people (various Function point organizations have certification schemes that require some degree of proficiency to pass).
Managers don’t seem to be interested in comparing estimated Story points against estimated time, preferring instead to track the rate at which Story points are implemented, e.g., velocity, or burndown. There are tiny amounts of data comparing Story points with time and Function points.
The available evidence suggests a relationship connecting Function points to actual time, and that Function points have similar error bounds to time estimates; the lack of data means that Story points are currently just a source of technobabble and number porn for management power-points (send me Story point data to help change this situation).
Estimation experiments: specification wording is mostly irrelevant
Existing software effort estimation datasets provide information about estimates made within particular development environments and with particular aims. Experiments provide a mechanism for obtaining information about estimates made under conditions of the experimenters choice, at least in theory.
Writing the code is sometimes the least time-consuming part of implementing a requirement. At hackathons, my default estimate for almost any non-trivial requirement is a couple of hours, because my implementation strategy is to find the relevant library or package and write some glue code around it. In a heavily bureaucratic organization, the coding time might be a rounding error in the time taken up by meeting, documentation and testing; so a couple of months would be considered normal.
If we concentrate on the time taken to implement the requirements in code, then estimation time and implementation time will depend on prior experience. I know that I can implement a lexer for a programming language in half-a-day, because I have done it so many times before; other people take a lot longer because they have not had the amount of practice I have had on this one task. I’m sure there are lots of tasks that would take me many days, but there is somebody who can implement them in half-a-day (because they have had lots of practice).
Given the possibility of a large variation in actual implementation times, large variations in estimates should not be surprising. Does the possibility of large variability in subject responses mean that estimation experiments have little value?
I think that estimation experiments can provide interesting information, as long as we drop the pretence that the answers given by subjects have any causal connection to the wording that appears in the task specifications they are asked to estimate.
If we assume that none of the subjects is sufficiently expert in any of the experimental tasks specified to realistically give a plausible answer, then answers must be driven by non-specification issues, e.g., the answer the client wants to hear, a value that is defensible, a round number.
A study by Lucas Gren and Richard Berntsson Svensson asked subjects to estimate the total implementation time of a list of tasks. I usually ignore software engineering experiments that use student subjects (this study eventually included professional developers), but treating the experiment as one involving social processes, rather than technical software know-how, makes subject software experience a lot less relevant.
Assume, dear reader, that you took part in this experiment, saw a list of requirements that sounded plausible, and were then asked to estimate implementation time in weeks. What estimate would you give? I would have thrown my hands up in frustration and might have answered 0.1 weeks (i.e., a few hours). I expected the most common answer to be 4 weeks (the number of weeks in a month), but it turned out to be 5 (a very ‘attractive’ round number), for student subjects (code+data).
The professional subjects appeared to be from large organizations, who I assume are used to implementations including plenty of bureaucratic stuff, as well as coding. The task specification did not include enough detailed information to create an accurate estimate, so subjects either assumed their own work environment or played along with the fresh-faced, keen experimenter (sorry Lucas). The professionals showed greater agreement in that the range of value given was not as wide as students, but it had a more uniform distribution (with maximums, rather than peaks, at 4 and 7); see below. I suspect that answers at the high end were from managers and designers with minimal coding experience.
What did the experimenters choose weeks as the unit of estimation? Perhaps they thought this expressed a reasonable implementation time (it probably is if it’s not possible to use somebody else’s library/package). I think that they could have chosen day units and gotten essentially the same results (at least for student subjects). If they had chosen hours as the estimation unit, the spread of answers would have been wider, and I’m not sure whether to bet on 7 (hours in a working day) or 10 being the most common choice.
Fitting a regression model to the student data shows estimates increasing by 0.4 weeks per year of degree progression. I was initially baffled by this, and then I realized that more experienced students expect to be given tougher problems to solve, i.e., this increase is based on self-image (code+data).
The stated hypothesis investigated by the study involved none of the above. Rather, the intent was to measure the impact of obsolete requirements on estimates. Subjects were randomly divided into three groups, with each seeing and estimating one specification. One specification contained four tasks (A), one contained five tasks (B), and one contained the same tasks as (A) plus an additional task followed by the sentence: “Please note that R5 should NOT be implemented” (C).
A regression model shows that for students and professions the estimate for (A) is about 1-2 weeks lower than (B), while (A) estimates are 3-5 weeks lower than (C) estimated.
What are subjects to make of an experimental situation where the specification includes a task that they are explicitly told to ignore?
How would you react? My first thought was that the ignore R5 sentence was itself ignored, either accidentally or on purpose. But my main thought is that Relevance theory is a complicated subject, and we are a very long way away from applying it to estimation experiments containing supposedly redundant information.
The plot below shows the number of subjects making a given estimate, in days; exp0to2 were student subjects (dashed line joins estimate that include a half-hour value, solid line whole hour), exp3 MSc students, and exp4 professional developers (code+data):
I hope that the authors of this study run more experiments, ideally working on the assumption that there is no connection between specification and estimate (apart from trivial examples).
The Approximate Number System and software estimating
The ability to perform simple numeric operations can improve the fitness of a creature (e.g., being able to select which branch contains the most fruit), increasing the likelihood of it having offspring. Studies have found that a wide variety of creatures have a brain subsystem known as the Approximate Number System (ANS).
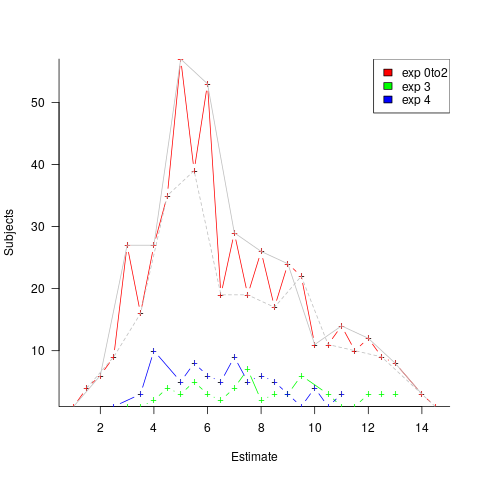
A study by Mechner rewarded rats with food, if they pressed a lever N times (with N taking one of the values 4, 8, 12 or 16), followed by pressing a second lever. The plot below shows the number of lever presses made before pressing the second lever, for a given required N; it suggests that the subject rat is making use of an approximate number system (code+data):
Humans have a second system for representing numbers, which is capable of exact representation, it is language. The Number Sense by Stanislas Dehaene was on my list of Christmas books for 2011.
One method used to study the interface between the two number systems, available to humans, involves subjects estimating the number of dots in a briefly presented image. While reading about one such study, I noticed that some of the plots showed patterns similar to the patterns seen in plots of software estimate/actual data. I emailed the lead author, Véronique Izard, who kindly sent me a copy of the experimental data.
The patterns I was hoping to see are those invariably seen in software effort estimation data, e.g., a power law relationship between actual/estimate, consistent over/under estimation by individuals, and frequent use of round numbers.
Psychologists reading this post may be under the impression that estimating the time taken to implement some functionality, in software, is a relatively accurate process. In practice, for short tasks (i.e., under a day or two) the time needed to form a more accurate estimate makes a good-enough estimate a cost-effective option.
This Izard and Dehaene study involved two experiments. In the first experiment, an image containing between 1 and 100 dots was flashed on the screen for 100ms, and subjects then had to type the estimated number of dots. Each of the six subjects participated in five sessions of 600 trials, with each session lasting about one hour; every number of dots between 1 and 100 was seen 30 times by each subject (for one subject the data contains 1,783 responses, other subjects gave 3,000 responses). Subjects were free to type any value as their estimate.
These kinds of studies have consistently found that subject accuracy is very poor (hardly surprising, given that subjects are not provided with any feedback to help calibrate their estimates). But since researchers are interested in patterns that might be present in the errors, very low accuracy is not an issue.
The plot below shows stimulus (number of dots shown) against subject response, with green line showing 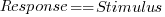 , and red line a fitted regression model having the form
, and red line a fitted regression model having the form 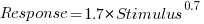 (which explains just over 70% of the variance; code+data):
(which explains just over 70% of the variance; code+data):
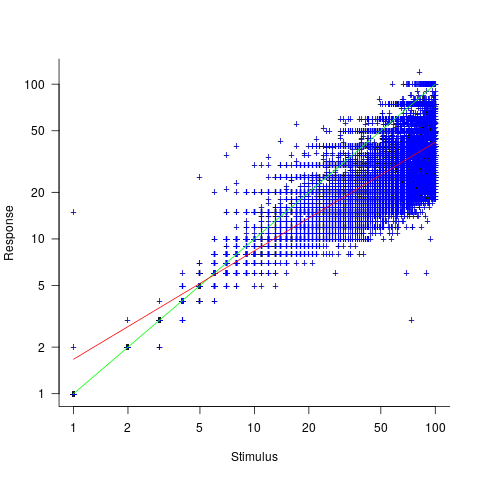
Just like software estimates, there is a good fit to a power law, and the only difference in accuracy performance is that software estimates tend not to be so skewed towards underestimating (i.e., there are a lot more low accuracy overestimates).
Adding subjectID to the model gives: 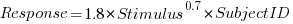 , with
, with 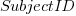 varying between 0.65 and 1.57; more than a factor of two difference between subjects (this model explains just under 90% of the variance). This is a smaller range than the software estimation data, but with only six subjects there was less chance of a wider variation (code+data).
varying between 0.65 and 1.57; more than a factor of two difference between subjects (this model explains just under 90% of the variance). This is a smaller range than the software estimation data, but with only six subjects there was less chance of a wider variation (code+data).
The software estimation data finds shows that accuracy does not improve with practice. The experimental subjects were not given any feedback, and would not be expected to improve, but does the strain of answering so many questions cause them to get worse? Adding trial number to the model suggests a 12% increase in underestimation, over 600 trials. However, adding an interaction with SubjectID shows that the performance of two subjects remains unchanged, while two subjects experience a 23% increase in underestimation.
The plot below shows the number of times each response was given, combining all subjects, with commonly given responses in red (code+data):
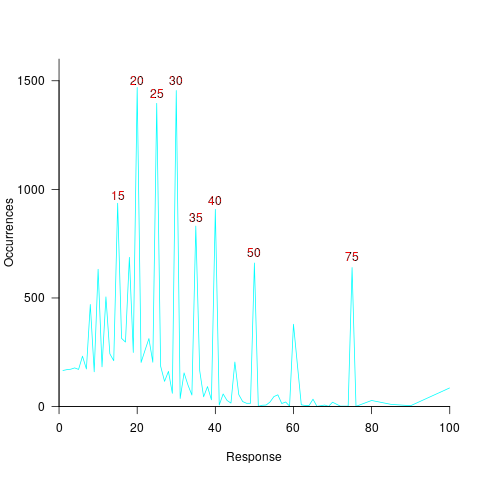
The commonly occurring values that appear in software estimation data are structured as fractions of units of time, e.g., 0.5 hours, or 1 hour or 1 day (appearing in the data as 7 hours). The only structure available to experimental subjects was subdivisions of powers of 10 (i.e., 10 and 100).
Analysing the responses by subject shows that each subject had their own set of preferred round numbers.
To summarize: The results from an experiment investigating the interface between the two human number systems contains three patterns seen in software estimation data, i.e., power law relationship between actual and estimate, individual differences in over/underestimating, and extensive use of round numbers.
Izard’s second experiment limited response values to prespecified values (i.e., one to 10 and multiples of 10), and gave a calibration example after each block of 46 trials. The calibration example improved performance, and the use of round numbers as prespecified response values had the effect of removing spikes from the response counts (which were relatively smooth; code+data)).
We now have circumstantial evidence that software developers are using the Approximate Number System when making software estimates. We will have to wait for brain images from a developer in an MRI scanner, while estimating a software task, to obtain more concrete proof that the ANS is involved in the process. That is, are the areas of the brain thought to be involved in the ANS (e.g., the intraparietal sulcus) active during software estimation?
Recent Comments