Archive
One code path dominates method execution
A recurring claim is that most reported faults are the result of coding mistakes in a small percentage of a program’s source code, with the 80/20 ‘rule’ being cited for social confirmation. I think there is something to this claim, but that the percentages are not so extreme.
A previous post pointed out that reported faults are caused by users. The 80/20 observation can be explained by users only exercising a small percentage of a program’s functionality (a tiny amount of data supports this observation). Surprisingly, there are researchers who believe that a small percentage of the code has some set of characteristics which causes it to contain most of a program’s coding mistakes (this belief has the advantage that a lot of source code is easily accessible and can be analysed to produce papers).
To what extent does user input direct program execution towards a small’ish subset of the code available to be executed?
The recent paper: Monitoring the Execution of 14K Tests: Methods Tend to Have One Path That Is Significantly More Executed by Andre Hora counted the number of times each path through a method’s source code was executed, when the method was called, for the 5,405 methods in 25 Python programs. These programs were driven by their 14,177 tests, rather than user input. The paper is focused on testing, in particular developer that developers tend to focus on positive tests.
Test suites are supposed to exercise all of a program’s source, so it is to be expected that these measurements will show a wider dispersion of code coverage than might be expected of typical user input.
The measurements also include a count of the lines executed/not executed along each executed method path. No information is provided on the number of unexecuted paths.
Within a method, there is always going to one path through the code that is executed more often than any other path. What this study found is that the most common path is often executed many more times than the other paths. The plot below shows, for each method (each +), the percentage of all calls to a method where the most common path was executed, against the total number of executed paths for that method; red/blue lines are fitted power law/exponential regression models, and the grey line shows the case where percentage executed is the fraction for a given number of paths (code+data):
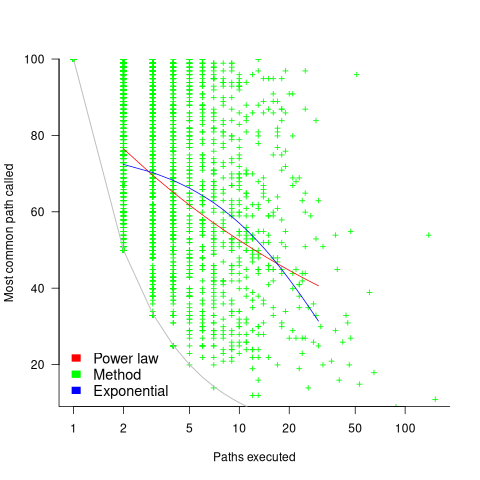
On average, the most common path is executed around four times more often than the second most commonly executed path.
While statistically significant, the fitted models do not explain much of the variance in the data. An argument can be made for either a power law and exponential distribution, and not having a feel for what to expect, I fitted both.
Non-error paths through a method have been found to be longer than the error paths. These measurements do not contain the information needed to attempt to replicate this finding.
New paths through a method are created by conditional statements, and the percentage of such statements in a method tends to be relatively constant across methods. The plot below shows the percentage of all calls to a method where the most common path was executed, where the method (each +) contains a given LOC; red/blue lines are fitted power law/exponential regression models (code+data):
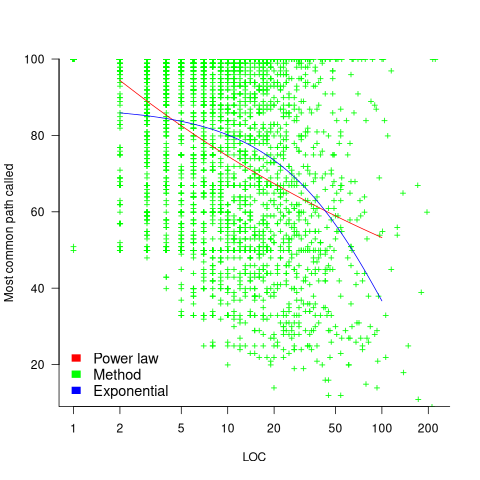
The models fitted to against LOC are better than those fitted against paths executed, but still not very good. A possible reason is that some methods will have unexecuted paths, LOC is a good proxy for total paths, and most common path percentage depends on total paths.
On average, 56% of a method’s LOC are executed along the most frequently executed path. When weighted by the number of method calls, the percentage is 48%.
The results of this study show that a call to most methods is likely to be dominated by the execution of one sequence of code. Another way that in which a small amount of code can dominate program execution is when most calls are to a small subset of the available methods. The plot below shows a density plot for the total number of calls to each method (code+data):

Around 62% of methods are called less than 100 times, while 2.6% are called over 10,000 times.
Small business programs: A dataset in the research void
My experience is that most of the programs created within organizations are very short, i.e., around 50–100 lines. Sometimes entire businesses are run using many short programs strung together in various ways. These short programs invariably make extensive use of the functionality provided by a much larger package that handles all the complicated stuff.
In the software development world, these short programs are likely to be shell scripts, but in the much larger ecosystem that is the business world these programs will be written in what used to be called a fourth generation language (4GL). These 4GLs are essentially domain specific languages for specific business tasks, such as report generation, or database query products, and for some time now spreadsheets.
The business software ecosystem is usually only studied by researchers in business schools, but short programs, business or otherwise, are rarely studied by any researchers. The source of such short programs is rarely publicly available; even if the information is not commercially confidential, the program likely addresses one group’s niche problem which is of no interest to anybody else, i.e., there is no rationale to publishing it. If source were available, there might not be enough of it to do any significant analysis.
I recently came across Clive Wrigley’s 1988 PhD thesis, which attempts to build a software estimation model. It contains summary data of 26 transaction processing systems written in the FOCUS language (an automated code generator).
For many organizations, there is a fundamental difference between business related problems and scientific/engineering problems, in that business problems tend to involve simple operations on lots of distinct data items (e.g., payroll calculation for each company employee), while scientific/engineering often involves a complicated formula operating on one set of data. There are exceptions.
4GLs enable technically proficient business users to create and maintain good enough applications without needing software engineering skills (yes, many do create spaghetti code), because they are not writing thousands of lines of code. The applications often contain many semi-self-contained subcomponents, which can be shared or swapped in/out. The small size makes it easier to change quickly, and there is direct access to the business users, it’s an agile process decades before this process took off in the world of non-4GL languages.
A major claim made by fans of 4GL is that it is much cheaper to create applications equivalent to those created using a 3GL, e.g., Cobol/C/C++/Java/Python/etc. I would agree that this true for small applications that fit the use-case addressed by a particular 4GL, but I think the domain specific nature of a 4GL will limit what can be done and likely need to be done in larger applications.
How do 4GL applications written in FOCUS compare against application written in Cobol? A 1987 paper by Chris Kemerer provides some manpower/LOC data for Cobol applications. I have no information on the amount of functionality in any of the applications. The plot below shows developer hours consumed creating 26 systems containing a given number of lines of code for FOCUS (green) and 15 COBOL (blue) programs, with fitted regression models in red (code+data):
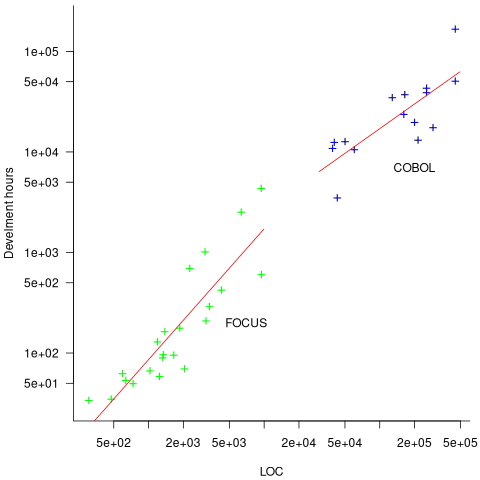
The two samples of applications differ by two orders of magnitude in LOC and developer hours, however, there is no information on the functionality provided by the applications.
Putnam’s software equation debunked
The implementation of a project has a lifecycle that starts and finishes with zero people working on it. Between starting and finishing, the number of staff quickly grows to a peak before slowly declining. In a series of very hard to obtain papers during the early 1960s (chapter 5), Peter Norden created a large project staffing model described by the Rayleigh equation. This model was evangelized by Lawrence Putnam in the 1970s, who called it the Norden/Rayleigh model, while others sometimes now call it the Norden/Putnam, Putnam/Rayleigh, or some combination of names; Putnam’s papers can be hard to obtain.
The Norden/Rayleigh equation is: 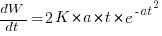
where: 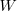 is work completed,
is work completed,  is total manpower over the lifespan of the project,
is total manpower over the lifespan of the project, 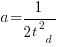 ,
, 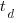 is time of maximum effort per unit time (i.e., the Norden/Rayleigh equation maximum value, which Putnam calls project development time), and
is time of maximum effort per unit time (i.e., the Norden/Rayleigh equation maximum value, which Putnam calls project development time), and  is project elapsed time.
is project elapsed time.
Norden’s model is only applicable to large projects (e.g., 2+ man-years), and Putnam points out that the staffing of small projects is usually a square wave, i.e., a number of staff are allocated at the start and this number remains the same until project completion.
As well as evangelizing Norden’s model, Putnam also created his own model; an equation connecting delivered lines of code, total manpower and project duration. The usually cited paper for this work is: “A General Empirical Solution to the Macro Software Sizing and Estimating Problem”, which can sometimes be found as a free download. I had always assumed that people did not take this model seriously, and it was not worth my time debunking it. The paper makes conjures hand-wavy connections between various equations which don’t seem to go anywhere, and eventually connects together a regression equation fitted to nine data points with an observation+assumption about another regression equation to create what Putnam calls the software equation: 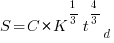 , where
, where  is delivered source code statements, and
is delivered source code statements, and  is a constant.
is a constant.
I recently read a 2014 paper by Han Suelmann debunking Putnam’s software equation, which led me to question my assumption about people not using Putnam’s model. Google Scholar shows 1,411 citations, with 133 since 2020. It looks like the software equation is still being taken seriously (or researchers are citing it because everybody else does; a common practice).
Why isn’t Putnam’s software equation worth treating seriously?
First, Putnam’s derivation of the software equation reads like a just-so story based on a tiny amount of data, and second a larger independent dataset does not show the pattern seen in Putnam’s data.
The derivation of the software equation starts by defining productivity as the number of delivered source code statements divided by the total manpower consumed to produce them, 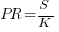 . Ok.
. Ok.
There is more certainty to a line fitted to a set of points that roughly follow a straight line, than to fit a line to points that follow a curve (because there are usually many ‘curve’ equations to choose from). The Norden/Rayleigh equation can be transformed to a form that is amenable to fitting a straight line, i.e., dividing by time and taking logs, as follows (which plugs in the value of  ):
):
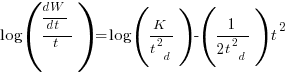
Putnam noticed (or perhaps it was the authors of the cited prepublication paper “Software budgeting model” by G. E. P. Box and L. Pallesen, which I cannot locate a copy of) that when plotting 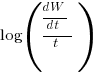 against
against 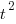 : “If the number
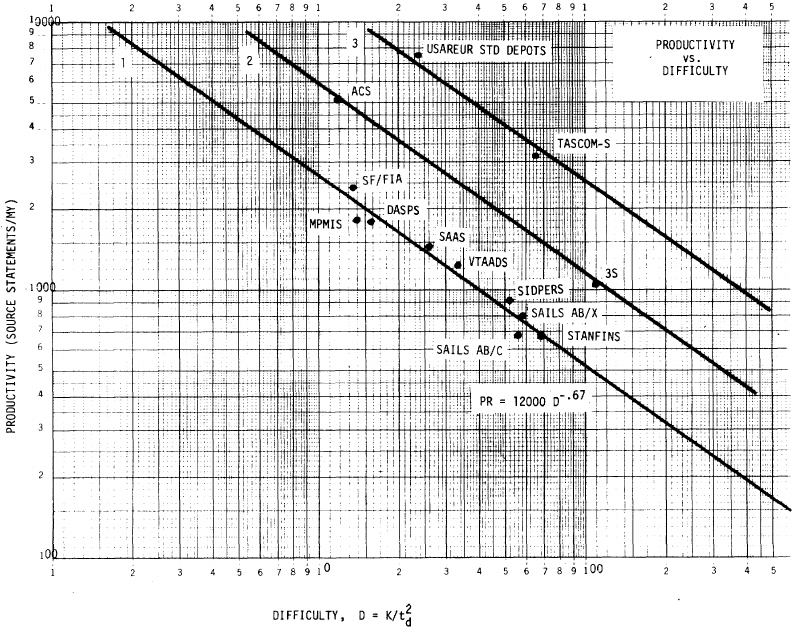
: “If the number 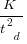 was small, it corresponded with easy systems; if the number was large, it corresponded with hard systems and appeared to fall in a range between these extremes.” Notice that in the screenshot of a figure from Putnam’s paper below, the y-axis is labelled “Difficulty”, not with the quantity actually plotted.
was small, it corresponded with easy systems; if the number was large, it corresponded with hard systems and appeared to fall in a range between these extremes.” Notice that in the screenshot of a figure from Putnam’s paper below, the y-axis is labelled “Difficulty”, not with the quantity actually plotted.
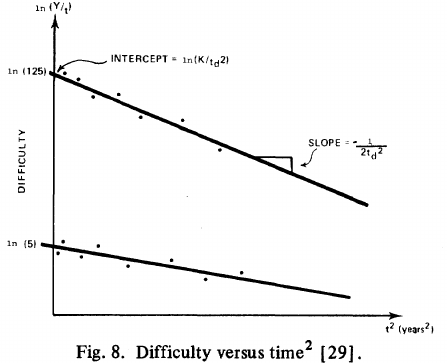
Based on an observation about easy/hard systems (it is never explained how easy/hard is measured) something called difficulty is defined to be: 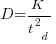 . No explanation is given for dropping the log scaling, or the possibility that some other relationship might hold.
. No explanation is given for dropping the log scaling, or the possibility that some other relationship might hold.
The screenshot below is of a figure from Putnam’s paper, which plots the values of 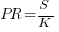 against
against 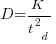 for 13 projects. The fitted regression lines (the three lines are fitted using, 9, 2 and 2 points of the 13 projects) have the form
for 13 projects. The fitted regression lines (the three lines are fitted using, 9, 2 and 2 points of the 13 projects) have the form 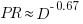 , i.e.,
, i.e., 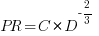 (I extracted the points and fitted
(I extracted the points and fitted 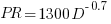 ; code+extracted data):
; code+extracted data):
With a bit of algebra, the two equations: 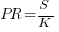 and
and 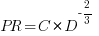 , can be combined to create the software equation.
, can be combined to create the software equation.
Yes, Putnam’s software equation was hand-waved into existence by plucking a “difficulty” component from an observation about the behavior of projects in a regression model and equating it to a regression line fitted to nine points.
Are the patterns seen by Putnam found in other projects?
In the 1987 paper “Time-Sensitive Cost Models in the Commercial MIS Environment” D. Ross Jeffery used data from 47 projects to investigate the effort/time relationships used by Putnam to derive his software equation.
The plot below, of log(Difficulty) vs log(Productivity), shows what appears to be a random scattering of points, confirmed by failing to fit a regression model (code+extracted data):
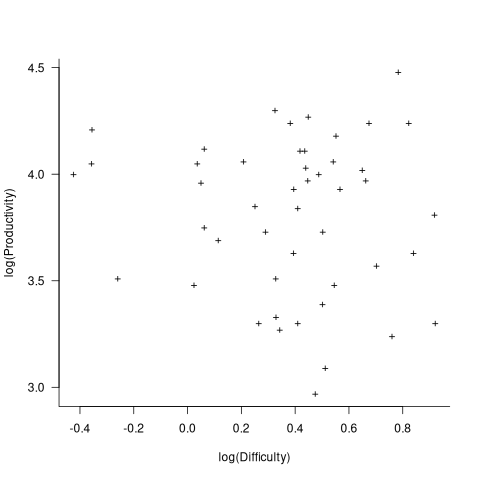
No. The patterns seen by Putnam are not present in these projects. I don’t think that the difference in application domain is relevant (Putnam’s projects were for Military systems and Jeffery’s are for commercial projects). Norden’s model is not specific to software projects.
Jeffery’s uses a regression model to find: 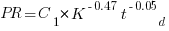 , the corresponding Putnam equation is:
, the corresponding Putnam equation is: 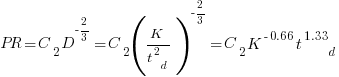 (the paper does not include the plot needed to extract the required data). The
(the paper does not include the plot needed to extract the required data). The  exponent might be claimed to be close enough, but the
exponent might be claimed to be close enough, but the 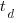 exponent is very different.
exponent is very different.
Jeffery’s paper includes a plot of 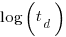 against
against 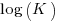 , and the plot below shows the extracted data (44 points), plus fitted regression line (code+extracted data):
, and the plot below shows the extracted data (44 points), plus fitted regression line (code+extracted data):
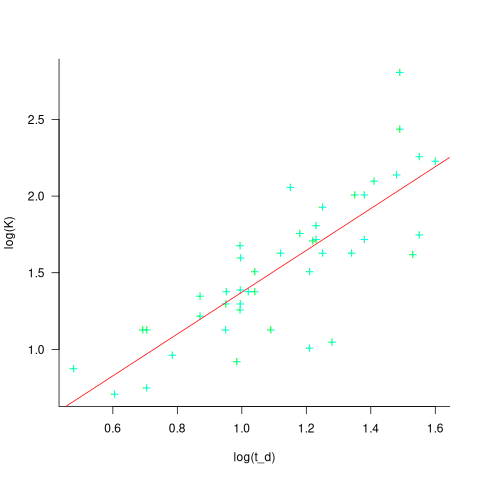
The regression line has the form 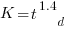 . This relationship further undermines assumptions made by Putnam, e.g., smaller systems are easier.
. This relationship further undermines assumptions made by Putnam, e.g., smaller systems are easier.
The Han Suelmann paper that triggered this post takes a very different approach to debunking Putnam’s model (he uses simulation to show that random data, drawn from a suitable distribution, can produce the patterns seen by Putnam).
Modeling program LOC growth with recurrence equations
Models predicting the growth, in lines of code, of a program are based on the assumption that future growth follows the same pattern of behavior as past growth. One such model is the recurrence relation:
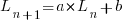 , where:
, where: 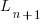 is LOC at time
is LOC at time 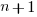 ,
, 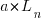 is the LOC carried over from release
is the LOC carried over from release  , and
, and  is the LOC added after release
is the LOC added after release  .
.
The solution to this recurrence relation is: 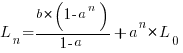 , where:
, where: 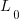 is the LOC at time
is the LOC at time 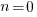 .
.
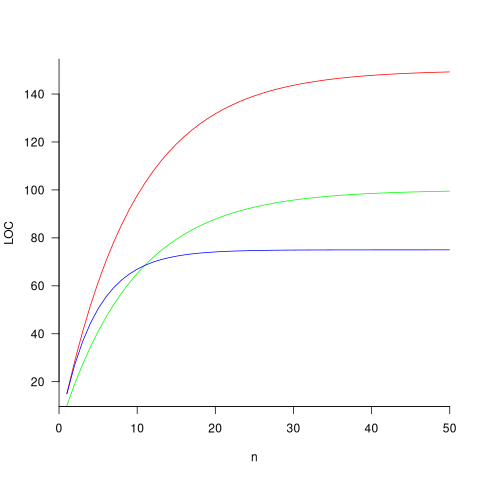
The plot below shows the growth predicted by this model, for various values of  and
and  (code+data):
(code+data):
How close is the fit between this model and actual project growth? The plot below shows the growth in LOC for FreeBSD between 1993 and 2006, data from Herraiz; the red line shows the above equation fitted using non-linear regression, with the blue line showing a fitted linear regression model of the form 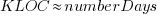 (code+data):
(code+data):
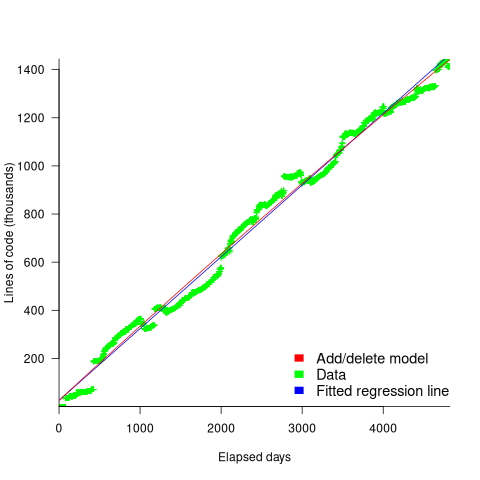
Plugging the fitted coefficients into the recurrence equation when 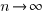 gives a prediction for the final maximum LOC in FreeBSD of:
gives a prediction for the final maximum LOC in FreeBSD of:
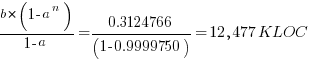
The FreeBSD growth is unusual in not having a slow start to its growth, or rather no data is available prior to 1993.
Long-lived, successful projects usually attract new developers, and over time some developers leave. The size of a project, and the predispositions of those involved, can limit the number of active core developers. The above model can be applied to the growth in the number of active developers, i.e.,
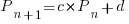 , where:
, where: 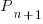 is active developers at time
is active developers at time 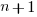 ,
, 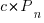 is the developers ceasing to be active
is the developers ceasing to be active  , and
, and 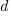 is the number of new active developers at
is the number of new active developers at  . The solution is:
. The solution is:
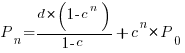
Adding the developer growth equation in to the LOC model, we get:
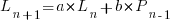 , where
, where  is now multiplied by the number of developers at time
is now multiplied by the number of developers at time 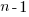 , i.e.,
, i.e., 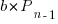 . The solution to these recurrence equations is somewhat involved (note: if you are using an LLM to check the answers, ChatGPT makes multiple mistakes, but the Grok response contains just one algebra mistake); when
. The solution to these recurrence equations is somewhat involved (note: if you are using an LLM to check the answers, ChatGPT makes multiple mistakes, but the Grok response contains just one algebra mistake); when 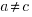 the equation is:
the equation is:
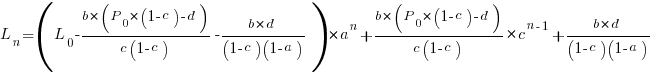
Checking this more complicated model against another project, the plot below shows the growth of the GNU C library between 1990 and 2011, data from Gonzalez-Barahona, Robles, Herraiz and Ortega; the red line is the fitted equation 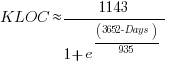 (code+data):
(code+data):
Unsurprisingly, I was not able to fit the more complicated growth model, using non-linear least squares, to the glibc LOC data. The problem was not being able to mimic the slow initial growth rate. I suspect that the developer growth model might be just wrong. Development work on a project does not last forever, and the number of developers will start decreasing at some point. For large projects, the Rayleigh distribution has been found to approximate staffing levels.
Data on project developer numbers over time is rare. The Linux kernel data shows an exponential developer growth rate, but I suspect that this is mostly caused by many one-time only developer contributing towards a new device driver (which are responsible for much of the Kernel growth).
Distribution of program sizes
Program size, in lines of code (LOC), used to be a topic of conversation among developers and managers. Program size is an issue when computer memory is measured in kilobytes. Large programs would be organized into overlays such that only small subsets needed to be held in memory at any time, i.e., programmer defined memory management.
Management used program size as a proxy for implementation effort/cost. Because size was a topic of conversation, it was possible to ask around to obtain a selection of values for the size of programs with similar functionality (accurate actual implementation costs were/are rarely available via the grapevine, but developers were/are always happy to talk about how small/large their programs were/are). These days, estimating LOC prior to implementation may appear more scientific, but I doubt it’s more accurate.
Once computers containing megabytes of memory became widespread, and the use of third-party libraries continued to grow, program size became a niche topic of conversation.
The size of some operating systems has become an occasional topic of conversation; it wasn’t previously because mainframe/mini computer manufacturers didn’t want customers talking about how much of their expensive memory was taken up by the OS. The size of Microsoft Windows leaked out and the Linux kernel is a topic of research.
Discussions around size have moved on from individual programs to the amount of space taken up by an installed application suite. Today, program size can be a rounding error compared to data files, extensions and add-ons.
Researchers have also moved on; repository size, in LOC/packages, is what now gets reported.
For those who are interested in program size; what is the distribution of program sizes? How many LOC are needed for a program to be above 50%, or in the top 95%?
Recent data on the size of individual programs is surprisingly hard to find, given how often LOC values appear in print. The one dataset I found is from the paper Empirical analysis of the relationship between CC and SLOC in a large corpus of Java methods and C functions, which is derived from the 2010’ish Sourcerer corpus of 13,103 Java projects (each of which I assume contains one program). The plot below shows the LOC (red) and methods (blue/green) for each program, in ascending order, along with values at various percentage points (code+data):
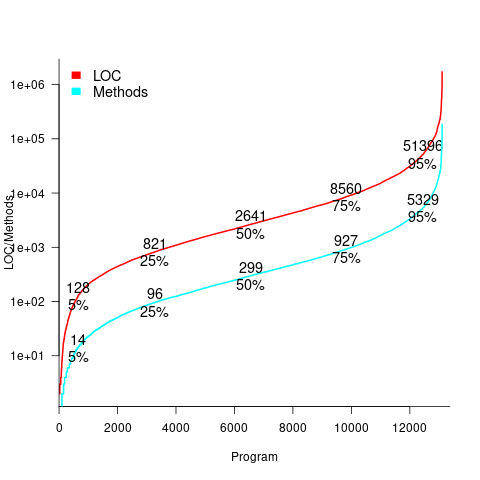
The size of Java programs is very likely to have increased since 2010. How much have grown? I don’t know.
What about the size of programs written in other languages?
I expect Python program size to be smaller, because the huge number of available package removes the need to implement a myriad of boilerplate functionality.
I expect C program size to be larger, both because of the smaller library ecosystem and because C programs tend to be older (programs rarely shrink with age).
Average lines added/deleted by commits across languages
Are programs written in some programming language shorter/longer, on average, than when written in other languages?
There is a lot of variation in the length of the same program written in the same language, across different developers. Comparing program length across different languages requires a large sample of programs, each implemented in different languages, and by many different developers. This sounds like a fantasy sample, given the rarity of finding the same specification implemented multiple times in the same language.
There is a possible alternative approach to answering this question: Compare the size of commits, in lines of code, for many different programs across a variety of languages. The paper: A Study of Bug Resolution Characteristics in Popular Programming Languages by Zhang, Li, Hao, Wang, Tang, Zhang, and Harman studied 3,232,937 commits across 585 projects and 10 programming languages (between 56 and 60 projects per language, with between 58,533 and 474,497 commits per language).
The data on each commit includes: lines added, lines deleted, files changed, language, project, type of commit, lines of code in project (at some point in time). The paper investigate bug resolution characteristics, but does not include any data on number of people available to fix reported issues; I focused on all lines added/deleted.
Different projects (programs) will have different characteristics. For instance, a smaller program provides more scope for adding lots of new functionality, and a larger program contains more code that can be deleted. Some projects/developers commit every change (i.e., many small commit), while others only commit when the change is completed (i.e., larger commits). There may also be algorithmic characteristics that affect the quantity of code written, e.g., availability of libraries or need for detailed bit twiddling.
It is not possible to include project-id directly in the model, because each project is written in a different language, i.e., language can be predicted from project-id. However, program size can be included as a continuous variable (only one LOC value is available, which is not ideal).
The following R code fits a basic model (the number of lines added/deleted is count data and usually small, so a Poisson distribution is assumed; given the wide range of commit sizes, quantile regression may be a better approach):
alang_mod=glm(additions ~ language+log(LOC), data=lc, family="poisson") dlang_mod=glm(deletions ~ language+log(LOC), data=lc, family="poisson") |
Some of the commits involve tens of thousands of lines (see plot below). This sounds rather extreme. So two sets of models are fitted, one with the original data and the other only including commits with additions/deletions containing less than 10,000 lines.
These models fit the mean number of lines added/deleted over all projects written in a particular language, and the models are multiplicative. As expected, the variance explained by these two factors is small, at around 5%. The two models fitted are (code+data):
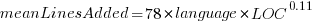 or
or 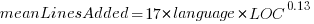 , and
, and 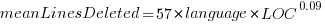 or
or 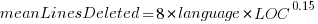 , where the value of
, where the value of 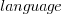 is listed in the following table, and
is listed in the following table, and 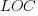 is the number of lines of code in the project:
is the number of lines of code in the project:
Original 0 < lines < 10000
Language Added Deleted Added Deleted
C 1.0 1.0 1.0 1.0
C# 1.7 1.6 1.5 1.5
C++ 1.9 2.1 1.3 1.4
Go 1.4 1.2 1.3 1.2
Java 0.9 1.0 1.5 1.5
Javascript 1.1 1.1 1.3 1.6
Objective-C 1.2 1.4 2.0 2.4
PHP 2.5 2.6 1.7 1.9
Python 0.7 0.7 0.8 0.8
Ruby 0.3 0.3 0.7 0.7 |
These fitted models suggest that commit addition/deletion both increase as project size increases, by around 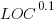 , and that, for instance, a commit in Go adds 1.4 times as many lines as C, and delete 1.2 as many lines (averaged over all commits). Comparing adds/deletes for the same language: on average, a Go commit adds
, and that, for instance, a commit in Go adds 1.4 times as many lines as C, and delete 1.2 as many lines (averaged over all commits). Comparing adds/deletes for the same language: on average, a Go commit adds 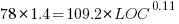 lines, and deletes
lines, and deletes 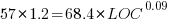 lines.
lines.
There is a strong connection between the number of lines added/deleted in each commit. The plot below shows the lines added/deleted by each commit, with the red line showing a fitted regression model 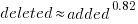 (code+data):
(code+data):
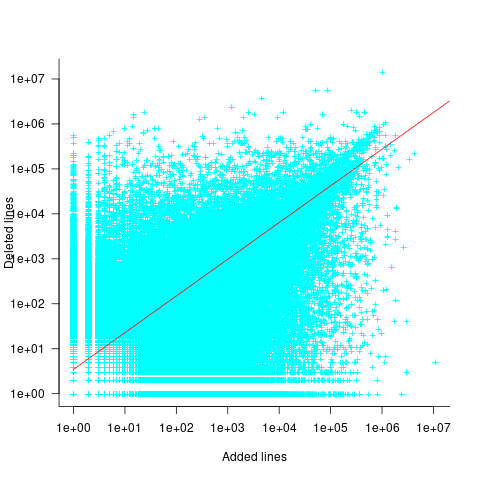
What other information can be included in a model? It is possible that project specific behavior(s) create a correlation between the size of commits; the algorithm used to fit this model assumes zero correlation. The glmer function, in the R package lme4, can take account of correlation between commits. The model component (language | project) in the following code adds project as a random effect on the language variable:
del_lmod=glmer(deletions ~ language+log(LOC)+(language | project), data=lc_loc, family=poisson) |
It takes around 24hr of cpu time to fit this model, which means I have not done much experimentation…
Some data on the size of Cobol programs/paragraphs
Before the internet took off in the 1990s, COBOL was the most popular language, measured in lines of code in production use. People who program in Cobol often have a strong business focus, and don’t hang out on sites used aggregated by surveys of programming language use; use of the language is almost completely invisible to those outside the traditional data processing community. So who knows how popular Cobol is today.
Despite the enormous quantity of Cobol code that has been written, very little Cobol source is publicly available (Open source or otherwise; the NIST compiler validation suite is not representative). The reason for the sparsity of source code is that Cobol programs are used to process business data, and the code is useless without the appropriate data (even with the data, the output is only likely to be of interest to a handful of people).
Program and function/method size (in LOC) are basic units of source code measurement. Until open source happened, published papers containing these measurements were based on small sample sizes and the languages covered was somewhat spotty. Cobol oriented research usually has a business orientation, rather than being programming oriented, and now there is a plentiful supply of source code written in non-Cobol languages.
I recently discovered appendix B of 1st Lt Richard E. Boone’s Master’s thesis An investigation into the use of software product metrics for COBOL systems (it’s post Rome period). Several days/awk scripts and editor macros later, LOC data for 178 programs containing 2,682 paragraphs containing 53,255 statements is now online (code+data).
A note on terminology: Cobol functions/methods are called paragraphs.
A paragraph is created by attaching a label to the first statement of the paragraph (there are no variables local to a paragraph; all variables are global). The statement PERFORM NAME-OF-PARAGRAPH ‘calls’ the paragraph labelled by NAME-OF-PARAGRAPH, somewhat like gosub number in BASIC.
It is possible to specify a sequence of paragraphs to be executed, in a PERFORM statement. The statement PERFORM NAME-OF-P1 THRU NAME-OF-P99 causes all paragraphs appearing textually in the code between the start of paragraph NAME-1 and the end of paragraph NAME-99 to be executed.
As far as I can tell, Boone’s measurements are based on individual paragraphs, not any sequences of paragraphs that are PERFORMed (it is likely that some labelled paragraphs are never PERFORMed in isolation).
Appendix B lists for each program: the paragraphs it contains, and for each paragraph the number of statements, McCabe’s complexity, maximum nesting, and Henry and Kafura’s Information flow metric
There are, based on naming, many EXIT paragraphs (711 or 26%); these are single statement paragraphs containing the statement EXIT. When encountered as the last paragraph of a PERFORM THU statement, the EXIT effectively acts like a procedure return statement; in other contexts, the EXIT statement acts like a continue statement.
In the following code the developer could have written PERFORM PARA-1 THRU PARA-4, but if a related paragraph was added between PARA-4 and PARA-END_EXIT all PERFORMs explicitly referencing PARA-4 would need to be checked to see if they needed updating to the new last paragraph.
START. PERFORM PARA-1 THRU PARA-END-EXIT. PARA-1. DISPLAY 'PARA-1'. PARA-2. DISPLAY 'PARA-2'. PARA-3. DISPLAY 'PARA-3'. P3-EXIT. EXIT. PARA-4. DISPLAY 'PARA-4'. PARA-END-EXIT. EXIT. |
The plot below shows the number of paragraphs containing a given number of statements, the red dot shows the count with EXIT paragraphs are ignored (code+data):

How does this distribution compare with that seen in C and Java? The plot below shows the Cobol data (in black, with frequency scaled-up by 1,000) superimposed on the same counts for C and Java (C/Java code+data):
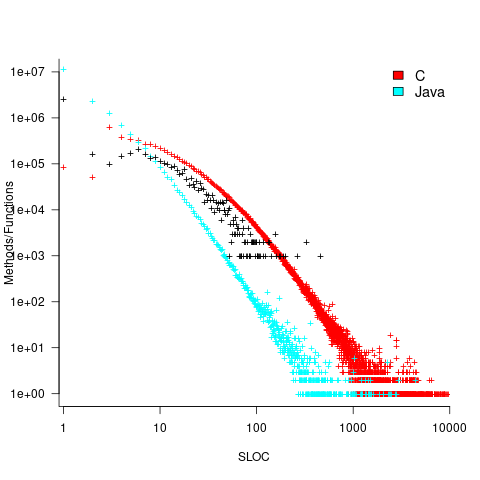
The distribution of statements per paragraph/function distribution for Cobol/C appears to be very similar, at least over the range 10-100. For less than 10-LOC the two languages have very different distributions. Is this behavior particular to the small number of Cobol programs measured? As always, more data is needed.
How many paragraphs does a Cobol program contain? The plot below shows programs ranked by the number of paragraphs they contain, including and excluding EXIT statements (code+data):
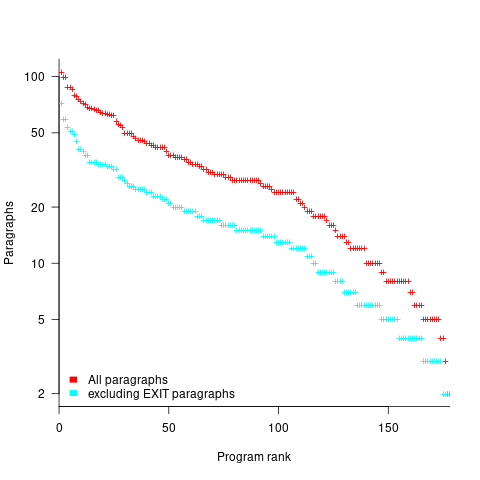
If you squint, it’s possible to imagine two distinct exponential declines, with the switch happening around the 100th program.
It’s tempting to draw some conclusions, but the sample size is too small.
Pointers to large quantities of Cobol source welcome.
Optimal function length: an analysis of the cited data
Careful analysis is required to extract reliable conclusions from data. Sloppy analysis can lead to incorrect conclusions being drawn.
The U-shaped plots cited as evidence for an ‘optimal’ number of LOC in a function/method that minimises the number of reported faults in a function, were shown to be caused by a mathematical artifact. What patterns of behavior are present in the data cited as evidence for an optimal number of LOC?
The 2000 paper Module Size Distribution and Defect Density by Malaiya and Denton summarises the data-oriented papers cited as sources on the issue of optimal length of a function/method, in LOC.
Note that the named unit of measurement in these papers is a module. In one paper, a module is specified as being as Ada package, but these papers specify that a module is a single function, method or anything else.
In order of publication year, the papers are:
The 1984 paper Software errors and complexity: an empirical investigation by Basili, and Perricone analyses measurements from a 90K Fortran program. The relevant Faults/LOC data is contained in two tables (VII and IX). Modules are sorted in to one of five bins, based on LOC, and average number of errors per thousand line of code calculated (over all modules, and just those containing at least one error); see table below:
Module Errors/1k lines Errors/1k lines
max LOC all modules error modules
50 16.0 65.0
100 12.6 33.3
150 12.4 24.6
200 7.6 13.4
>200 6.4 9.7 |
One of the paper’s conclusions: “One surprising result was that module size did not account for error proneness. In fact, it was quite the contrary–the larger the module, the less error-prone it was.”
The 1985 paper Identifying error-prone software—an empirical study by Shen, Yu, Thebaut, and Paulsen analyses defect data from three products (written in Pascal, PL/S, and Assembly; there were three versions of the PL/S product) were analysed using Halstead/McCabe, plus defect density, in an attempt to identify error-prone software.
The paper includes a plot (figure 4) of defect density against LOC for one of the PL/S product releases, for 108 modules out of 253 (presumably 145 modules had no reported faults). The plot below shows defects against LOC, the original did not include axis values, and the red line is the fitted regression model 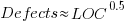 (data extracted using WebPlotDigitizer; code+data):
(data extracted using WebPlotDigitizer; code+data):
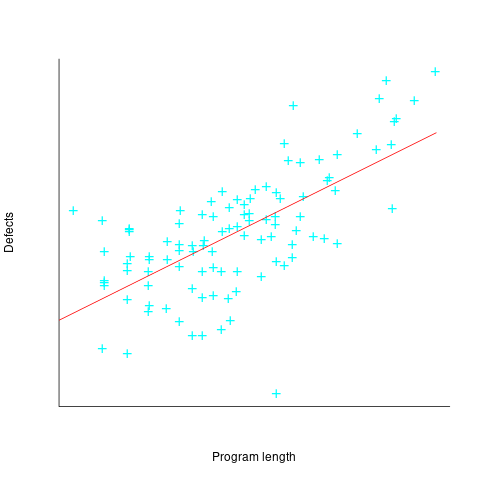
The power-law exponent is less than one, which suggests that defects per line is decreasing as module size increases, i.e., there is no optimal minimum, larger is always better. However, the analysis is incomplete because it does not include modules with zero reported defects.
The authors say: “… that there is a higher mean error rate in smaller sized modules, is consistent with that discovered by Basili and Perricone.”
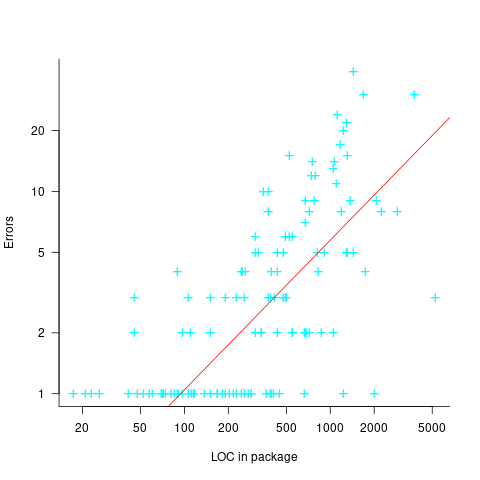
The 1990 paper Error Density and Size in Ada Software by Carol Withrow analyses error data from a 114 KLOC military communication system written in Ada; of the 362 Ada packages, 137 had at least one error. The unit of measurement is an Ada package, which like a C++ class, can contain multiple definitions of types, variables, and functions.
The paper plots errors per thousand line of code against LOC, for packages containing at least one error, i.e., 62% of packages are not included in the analysis. The 137 packages are sorted into 8-bins, based on the number of lines they contain. The 52 packages in the 159-251 LOC bin have an average of 1.8 errors per 1 KLOC, which is the lowest bin average. The author concludes: “Our study of a large Ada project shows this optimal size to be about 225 lines.”
The plot below shows errors against LOC, red line is the fitted regression model 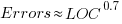 for
for 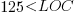 (data extracted using WebPlotDigitizer from figure 2; code+data):
(data extracted using WebPlotDigitizer from figure 2; code+data):
The 1993 paper An Empirical Investigation of Software Fault Distribution by Moller, and Paulish analysed four versions of a 750K product for controlling computer system utilization, written in assembler; the items measured were: DLOC (‘delta’ lines of code, DLOC, defined as “… the number of added or modified source lines of code for a version as compared to the prior version.”) and fault rate (faults per DLOC).
This paper is the first to point out that the code from multiple modules may need to be modified to fix a defect/fault/error. The following table shows the percentage of faults whose correction required changes to a given number of modules, for three releases of the product.
Modules
Version 1 2 3 4 5 6
a 78% 14% 3.4% 1.3% 0.2% 0.1%
b 77% 18% 3.3% 1.1% 0.3% 0.4%
c 85% 12% 2.0% 0.7% 0.0% 0.0% |
Modules are binned by DLOC and various plots appear in the paper; it’s all rather convoluted. The paper summary says: “With modified code, the fault rates steadily decrease as the module size increases.”
What conclusions does the Malaiya and Denton paper draw from these papers?
They present “… a model giving influence of module size on defect density based on data that has been reported. It provides an interpretation for both declining defect density for smaller modules and gradually rising defect density for larger modules. … If small modules can be
combined into optimal sized modules without reducing cohesion significantly, than the inherent defect density may be significantly reduced.”
The conclusion I draw from these papers is that a sloppy analysis in one paper obtained a result that sounded interesting enough to get published. All the other papers find defect/error/fault rate decreasing with module size (whatever a module might be).
Analysis of when refactoring becomes cost-effective
In a cost/benefit analysis of deciding when to refactor code, which variables are needed to calculate a good enough result?
This analysis compares the excess time-code of future work against the time-cost of refactoring the code. Refactoring is cost-effective when the reduction in future work time is less than the time spent refactoring. The analysis finds a relationship between work/refactoring time-costs and number of future coding sessions.
Linear, or supra-linear case
Let’s assume that the time needed to write new code grows at a linear, or supra-linear rate, as the amount of code increases (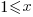 ):
):
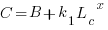
where: 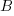 is the base time for writing new code on a freshly refactored code base,
is the base time for writing new code on a freshly refactored code base, 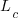 is the number of lines of code that have been written since the last refactoring, and
is the number of lines of code that have been written since the last refactoring, and 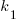 and
and  are constants to be decided.
are constants to be decided.
The total time spent writing code over  sessions is:
sessions is:
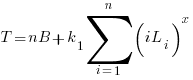
If the same number of new lines is added in every coding session, 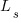 , and
, and  is an integer constant, then the sum has a known closed form, e.g.:
is an integer constant, then the sum has a known closed form, e.g.:
x=1, 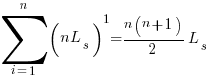 ; x=2,
; x=2, 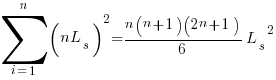
Let’s assume that the time taken to refactor the code written after  sessions is:
sessions is:
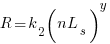
where: 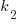 and
and  are constants to be decided.
are constants to be decided.
The reason for refactoring is to reduce the time-cost of subsequent work; if there are no subsequent coding sessions, there is no economic reason to refactor the code. If we assume that after refactoring, the time taken to write new code is reduced to the base cost, 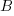 , and that we believe that coding will continue at the same rate for at least another
, and that we believe that coding will continue at the same rate for at least another  sessions, then refactoring existing code after
sessions, then refactoring existing code after  sessions is cost-effective when:
sessions is cost-effective when:
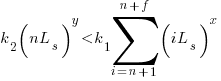
assuming that  is much smaller than
is much smaller than  , setting
, setting 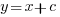 , and rearranging we get:
, and rearranging we get:
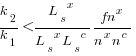
after rearranging we obtain a lower limit on the number of future coding sessions,  , that must be completed for refactoring to be cost-effective after session
, that must be completed for refactoring to be cost-effective after session  ::
::
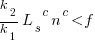
It is expected that 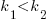 ; the contribution of code size, at the end of every session, in the calculation of
; the contribution of code size, at the end of every session, in the calculation of  and
and 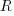 is equal (i.e.,
is equal (i.e., 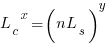 ), and the overhead of adding new code is very unlikely to be less than refactoring all the newly written code.
), and the overhead of adding new code is very unlikely to be less than refactoring all the newly written code.
With 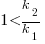 ,
,  must be close to zero; otherwise, the likely relatively large value of
must be close to zero; otherwise, the likely relatively large value of 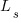 (e.g., 100+) would produce surprisingly high values of
(e.g., 100+) would produce surprisingly high values of  .
.
Sublinear case
What if the time overhead of writing new code grows at a sublinear rate, as the amount of code increases?
Various attributes have been found to strongly correlate with the 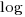 of lines of code. In this case, the expressions for
of lines of code. In this case, the expressions for  and
and 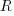 become:
become:
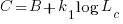
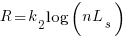
and the cost/benefit relationship becomes:

applying Stirling’s approximation and simplifying (see Exact equations for sums at end of post for details) we get:
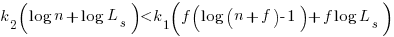
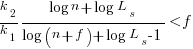
applying the series expansion (for 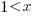 ):
): 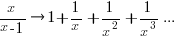 , we get
, we get
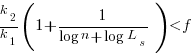
Discussion
What does this analysis of the cost/benefit relationship show that was not obvious (i.e., the relationship 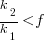 is obviously true)?
is obviously true)?
What the analysis shows is that when real-world values are plugged into the full equations, all but two factors have a relatively small impact on the result.
A factor not included in the analysis is that source code has a half-life (i.e., code is deleted during development), and the amount of code existing after  sessions is likely to be less than the
sessions is likely to be less than the 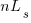 used in the analysis (see Agile analysis).
used in the analysis (see Agile analysis).
As a project nears completion, the likelihood of there being  more coding sessions decreases; there is also the every present possibility that the project is shutdown.
more coding sessions decreases; there is also the every present possibility that the project is shutdown.
The values of 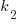 and
and 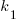 encode information on the skill of the developer, the difficulty of writing code in the application domain, and other factors.
encode information on the skill of the developer, the difficulty of writing code in the application domain, and other factors.
Exact equations for sums
The equations for the exact sums, for 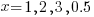 , are:
, are:
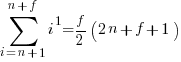
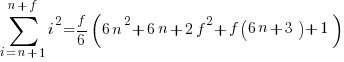
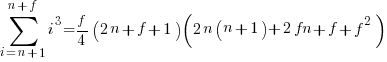
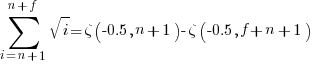 , where
, where 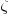 is the Hurwitz zeta function.
is the Hurwitz zeta function.
Sum of a log series: 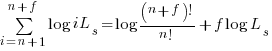
using Stirling’s approximation we get
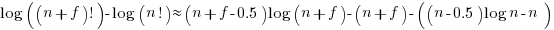
simplifying
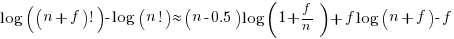
and assuming that  is much smaller than
is much smaller than  gives
gives
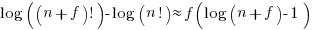
Another nail for the coffin of past effort estimation research
Programs are built from lines of code written by programmers. Lines of code played a starring role in many early effort estimation techniques (section 5.3.1 of my book). Why would anybody think that it was even possible to accurately estimate the number of lines of code needed to implement a library/program, let alone use it for estimating effort?
Until recently, say up to the early 1990s, there were lots of different computer systems, some with multiple (incompatible’ish) operating systems, almost non-existent selection of non-vendor supplied libraries/packages, and programs providing more-or-less the same functionality were written more-or-less from scratch by different people/teams. People knew people who had done it before, or even done it before themselves, so information on lines of code was available.
The numeric values for the parameters appearing in models were obtained by fitting data on recorded effort and lines needed to implement various programs (63 sets of values, one for each of the 63 programs in the case of COCOMO).
How accurate is estimated lines of code likely to be (this estimate will be plugged into a model fitted using actual lines of code)?
I’m not asking about the accuracy of effort estimates calculated using techniques based on lines of code; studies repeatedly show very poor accuracy.
There is data showing that different people implement the same functionality with programs containing a wide range of number of lines of code, e.g., the 3n+1 problem.
I recently discovered, tucked away in a dataset I had previously analyzed, developer estimates of the number of lines of code they expected to add/modify/delete to implement some functionality, along with the actuals.
The following plot shows estimated added+modified lines of code against actual, for 2,692 tasks. The fitted regression line, in red, is: 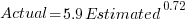 (the standard error on the exponent is
(the standard error on the exponent is 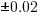 ), the green line shows
), the green line shows 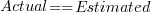 (code+data):
(code+data):
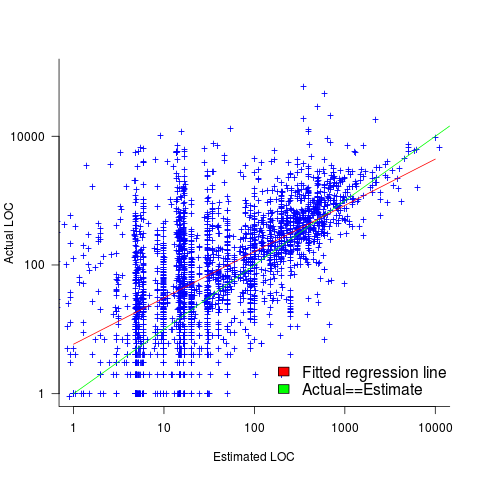
The fitted red line, for lines of code, shows the pattern commonly seen with effort estimation, i.e., underestimating small values and over estimating large values; but there is a much wider spread of actuals, and the cross-over point is much further up (if estimates below 50-lines are excluded, the exponent increases to 0.92, and the intercept decreases to 2, and the line shifts a bit.). The vertical river of actuals either side of the 10-LOC estimate looks very odd (estimating such small values happen when people estimate everything).
My article pointing out that software effort estimation is mostly fake research has been widely read (it appears in the first three results returned by a Google search on software fake research). The early researchers did some real research to build these models, but later researchers have been blindly following the early ‘prophets’ (i.e., later research is fake).
Lines of code probably does have an impact on effort, but estimating lines of code is a fool’s errand, and plugging estimates into models built from actuals is just crazy.
Recent Comments