Archive
A surprising retrospective task estimation dataset
When estimating the time needed to implement a task, the time previously needed to implement similar tasks provides useful guidance. The implementation time for these previous tasks may itself be estimated, because the actual time was not measured or this information is currently unavailable.
How accurate are developer time estimates of previously completed tasks?
I am not aware of any software related dataset of estimates of previously completed tasks (it’s hard enough finding datasets containing information on the actual implementation time). However, I recently found the paper Dynamics of retrospective timing: A big data approach by Balcı, Ünübol, Grondin, Sayar, van Wassenhove, and Wittmann. The data analysed comes from a survey questionnaire, where 24,494 people estimated the how much time they had spent answering the questions, along with recording the current time at the start/end of the questionnaire. The supplementary data is in MATLAB format, and is also available as a csv file in the Blursday database (i.e., RT_Datasets).
Some of the behavior patterns seen in software engineering estimates appear to be general human characteristics, e.g., use of round numbers. An analysis of the estimation performance of a wide sample of the general population could help separate out characteristics that are specific to software engineering and those that apply to the general population.
The following table shows the percentage of answers giving a particular Estimate and Actual time, in minutes. Over 60% of the estimates are round numbers. Actual times are likely to be round numbers because people often give a round number when asked the time (code+data):
Minutes Estimate Actual
20 18% 8.5%
15 15% 5.3%
30 12% 7.6%
25 10% 6.2%
10 7.7% 2.1% |
I was surprised to see that the authors had fitted a regression model with the Actual time as the explanatory variable and the Estimate as the response variable. The estimation models I have fitted always have the roles of these two variables reversed. More of this role reversal difference below.
The equation fitted to the data by the authors is (they use the term Elapsed, for consistency with other blog articles I continue to use Actual; code+data):
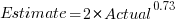
This equation says that, on average, for shorter Actual times the Estimate is higher than the Actual, while for longer Actual times the average Estimate is lower.
Switching the roles of the variables, I expected to see a fitted model whose coefficients are somewhat similar to the algebraically transformed version of this equation, i.e.,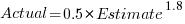 
. At the very least, I expected the exponent to be greater than one.
Surprisingly, the equation fitted with the variables roles reversed is very similar, i.e., the equations are the opposite of each other:
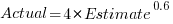
This equation says that, on average, for shorter Estimate times the Actual time is higher than the Estimate, while for longer Estimate times the average Actual is lower, i.e., the opposite behavior specifie dby the earlier equation.
I spent some time trying to understand how it was possible for data to be fitted such that (x ~ y) == (y ~ x), even posting a question to Cross Validated. I might, in a future post, discuss the statistical issues behind this behavior.
So why did the authors of this paper treat Actual as an explanatory variable?
After a flurry of emails with the lead author, Fuat Balcı (who was very responsive to my questions), where we both doubled checked the code/data and what we thought was going on, Fuat answered that (quoted with permission):
“The objective duration is the elapsed time (noted by the experimenter based on a clock reading), and the estimate is the participant’s response. According to the psychophysical approach the mapping between objective and subjective time can be defined by regressing the subjective estimates of the participants on the objective duration noted by the experimenter. Thus, if your research question is how human’s retrospective experience of time changes with the duration of events (e.g., biases in time judgments), the y-axis should be the participant’s response and the x-axis should be the actual duration.”
This approach has a logic to it, and is consistent with the regression modelling done by other researchers who study retrospective time estimation.
So which modelling approach is correct, and are people overestimating or underestimating shorter actual time durations?
Going back to basics, the structure of this experiment does not produce data that meets one of the requirements of the statistical technique we are both using (ordinary least squares) to fit a regression model. To understand why ordinary least squares, OLS, is not applicable to this data, it’s necessary to delve into a technical detail about the mathematics of what OLS does.
The equation actually fitted by OLS is: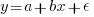 
, where 
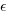is an error term (i.e., ‘noise’ caused by all the effects other than 
). The value of is assumed to be exact, i.e., not contain any ‘noise’.
Usually, in a retrospective time estimation experiment, subjects hear, for instance, a sound whose duration is decided in advance by the experimenter; subjects estimate how long each sound lasted. In this experimental format, it makes sense for the Actual time to appear on the right-hand-side as an explanatory variable and for the Estimate response variable on the left-hand-side.
However, for the questionnaire timing data, both the Estimate and Actual time are decided by the person giving the answers. There is no experimenter controlling one of the values. Both the Estimate and Actual values contain ‘noise’. For instance, on a different day a person may have taken more/less time to actually answer the questionnaire, or provided a different estimate of the time taken.
The correct regression fitting technique to use is errors-in-variables. An errors-in-variables regression fits the equation: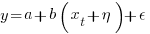 
, where: 
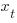is the true value of and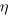 
is its associated error. A selection of packages are available for fitting a variety of errors-in-variables models.
I regularly see OLS used in software engineering papers (including mine) where errors-in-variables is the technically correct technique to use. Researchers are either unaware of the error issues or assuming that the difference is not important. The few times I have fitted an errors-in-variables model, the fitted coefficients have not been much different from those fitted by an OLS model; for this dataset the coefficient difference is obviously important.
The complication with building an errors-in-variables model is that values need to be specified for the error terms 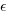and 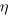. With OLS the value of 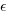is produced as part of the fitting process.
How might the required error values be calculated?
If some subjects round reported start/stop times, there may not be any variation in reported Actual time, or it may jump around in 5-minute increments depending on the position of the minute hand on the clock.
Learning researchers have run experiments where each subject performs the same task multiple times. Performance improves with practice, which makes it difficult to calculate the likely variability in the first-time performance. If we assume that performance is skill based, the standard deviation of all the subjects completing within a given timeframe could be used to calculate an error term.
With 60% of Estimates being round numbers, there might not be any variation for many people, or perhaps the answer given will change to a different round number. There is Estimate data for different, future tasks, and a small amount of data for the same future tasks. There is data from many retrospective studies using very short time intervals (e.g., tens of seconds), which might be applicable.
We could simply assume that the same amount of error is present in each variable. Deming regression is an errors-in-variables technique that supports this approach, and does not require any error values to be specified. The following equations have been fitted using Deming regression (code+data):
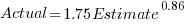
and
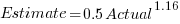
While these two equations are consistent with each other, we don’t know if the assumption of equal errors in both variables is realistic.
What next?
Hopefully it will be possible to work out reasonable error values for the Actual/Estimate times. Fitting a model using these values will tell us wether any over/underestimating is occurring, and the associated span of time durations.
I also need to revisit the analysis of software task estimation times.
What is known about software effort estimation in 2024
It’s three years since my 2021 post summarizing what I knew about estimating software tasks. While no major new public datasets have appeared (there have been smaller finds), I have talked to lots of developers/managers about the findings from the 2019/2021 data avalanche, and some data dots have been connected.
A common response from managers, when I outline the patterns found, is some variation of: “That sounds about right.” While it’s great to have this confirmation, it’s disappointing to be telling people what they already know, even if I can put numbers to the patterns.
Some of the developer behavior patterns look, to me, to be actionable, e.g., send developers on a course to unbias their estimates. In practice, managers are worried about upsetting developers or destabilising teams. It’s easy for an unhappy developer to find another job (the speakers at the meetups I attend often end by saying: “and we’re hiring.”)
This post summarizes a talk I gave recently on what is known about software estimating; a video will eventually appear on the British Computer Society‘s Software Practice Advancement group’s YouTube channel, and the slides are on Github.
What I call the historical estimation models contain source code, measured in lines, as a substantial component, e.g., COCOMO which overfits a miniscule dataset. The problem with this approach is that estimates of the LOC needed to implement some functionality LOC are very inaccurate, and different developers use different LOC to implement the same functionality.
Most academic research in software effort estimation continues to be based on miniscule datasets; it’s essentially fake research. Who is doing good research in software estimating? One person: Magne Jørgensen.
Almost all the short internal task estimate/actual datasets contain all the following patterns:
- use of round-numbers (known as heaping in some fields). The ratios of the most frequently used round numbers, when estimating time, are close to the ratios of the Fibonacci sequence,
- short tasks tend to be under-estimated and long tasks over-estimate. Surprisingly, the following equation is a good fit for many time-based datasets:
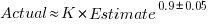, - individuals tend to either consistently over or under estimate (this appears to be connected with the individual’s risk profile),
- around 30% of estimates are accurate, 68% within a factor of two, and 95% within a factor of four; one function point dataset, one story point dataset, many time datasets,
- developer estimation accuracy does not change with practice. Possible reasons for this include: variability in the world prevents more accurate estimates, developers choose to spend their learning resources on other topics (such as learning more about the application domain).
I have a new ChatGPT generated image for my slide covering the #Noestimates movement:
Motivation and software development
If people were not motivated to write software, computers would not have anything to do. What motivates a person to write software?
The source of human motivation may be intrinsic, as when pleasure is derived from performing the activity, or it may be extrinsic, such as being paid.
For some developers, writing software is a hedonistic activity. Intrinsic motivation continues to be the attractive force behind very many Open source projects.
People have to make a living, and being paid to write software creates an extrinsic motivation.
What do we know about human motivation?
The 1943 paper A Theory of Human Motivation introduced Maslow’s hierarchy of needs, which is now often used as a structure for thinking about motivation. The image below, from Wikipedia, shows Maslow’s hierarchy:
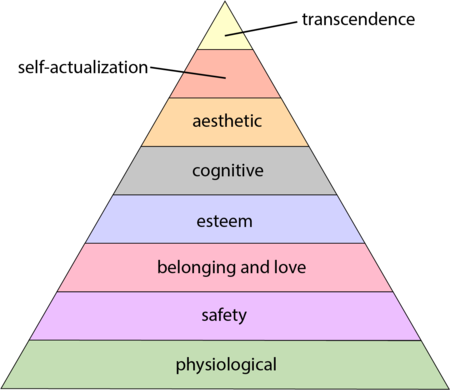
Managers have long known that various kinds of carrots & sticks can be used to incentivize people to behave in a particular way, i.e., applying extrinsic motivation.
Incentives are actively researched in business and marketing departments. Unfortunately, sometimes more fashionable topics, such as cognitive biases, divert researcher’s interest.
Despite its fundamental importance, developer motivation is rarely considered, let alone a subject of research, within computing departments.
As purveyors of intangible goods, the software industry is aware of many issues around motivation. Managers of software teams appreciate the impact of team motivation on performance. Team motivation is a perennial topic of discussion for the Agile coaches and Scrum masters I meet. Companies selling products offering an API hire developer evangelists, whose job is to motivate third-party developers to use this API.
Software systems that continue to be used become part of the fabric of larger, more complex, systems. The motivations of the inhabitants of complex systems can have many unintended consequences.
Motivation is an intangible that cannot be measured directly; its effect has to be inferred from the results produced by the behaviors it drives. Distinguishing between two diametrically different motivations can present a conundrum, e.g., distinguishing between developers following Parkinson’s law or striving to meet a deadline.
Books don’t usually have much to say about the human side of software product management. A well-known exception is Peopleware: Productive Projects and Teams.
My evidence-based software engineering book should have had a chapter devoted to motivation, but given its focus on publicly available data, I had to make do with several 1-page subsections.
Printing press+widespread religious behavior: A theory
The book The Weirdest People in the World: How the West Became Psychologically Peculiar and Particularly Prosperous provides an explanation of the processes which weakened the existing social ties of family and tribe; however, the emergence of WEIRD people (Western, Educated, Industrialized, Rich and Democratic) required new social norms to spread and be accepted throughout society. A major technical innovation, in the form of the printing press, provided the means for mass communication of ideas and practices.
David High-Jones’ book Wyclif’s Dust: Western Cultures from the Printing Press to the Present describes the social consequences of what he calls book religion; a combination of deeply religious western societies and the ability of individuals to write and sell affordable books (made possible by the printing press). Religion+printing press created the conditions for what High-Jones calls a hothouse culture, a period from the 1600s to the end of the 1800s.
Around 1440 the printing press is invented and quickly spreads; around 5 million books were handwritten in the 1400s, about 80 million books were produced in the first 50 years of printing, and around a billion in the 1700s. During the 1500s the Protestant reformation happens; Protestant encouraged its followers to read the Bible, which creates a demand for printed Bibles and the need to be able to read (which increases literacy rates). In England, between 1480-1640, 40% of published books were religious.
The changes to society’s existing norms are wrought by cultural transmission, initially via middle class parents making use of edifying books to teach their children moral values and social skills, later Sunday schools took on this role, but also had to offer reading lessons to attract members. In the adult world, accepted norms were maintained by social enforcement. The impact on western societies was widespread because observant religious behavior was widespread.
The original intent, of those writing the religious books, was the creation of a god fearing society. In practice, a trust based society was created, where workers might be relied upon not to shirk their duties and businessmen to not renege on agreements.
In the beginning science, in the form of printed technical books, rarely made an appearance. In the 1700s the Enlightenment happens, and scientific books are discussed by small collections of disparate individuals. The industrial revolution happens, but the bulk of the demand is for trustworthy workers; technical and scientific know how remains a minority interest.
In Part I of the book, High-Jones weaves a reading and convincing narrative. Part II, 1900 to today, is a tale of the crumbling and breakdown of the social forces and incentives that creates the trust based society; while example are enumerated, no overarching theory is proposed (I skimmed this part).
Task backlog waiting times are power laws
Once it has been agreed to implement new functionality, how long do the associated tasks have to wait in the to-do queue?
An analysis of the SiP task data finds that waiting time has a power law distribution, i.e.,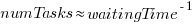 
, where 
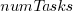is the number of tasks waiting a given amount of time; the LSST:DM Sprint/Story-point/Story has the same distribution. Is this a coincidence, or does task waiting time always have this form?
Queueing theory analyses the properties of systems involving the arrival of tasks, one or more queues, and limited implementation resources.
A basic result of queueing theory is that task waiting time has an exponential distribution, i.e., not a power law. What software task implementation behavior is sufficiently different from basic queueing theory to cause its waiting time to have a power law?
As always, my first line of attack was to find data from other domains, hopefully with an accompanying analysis modelling the behavior. It’s possible that my two samples are just way outside the norm.
Eventually I found an analysis of the letter writing response time of Darwin, Einstein and Freud (my email asking for the data has not yet received a reply). Somebody writes to a famous scientist (the scientist has to be famous enough for people to want to create a collection of their papers and letters), the scientist decides to add this letter to the pile (i.e., queue) of letters to reply to, eventually a reply is written. What is the distribution of waiting times for replies? Yes, it’s a power law, but with an exponent of -1.5, rather than -1.
The change made to the basic queueing model is to assign priorities to tasks, and then choose the task with the highest priority (rather than a random task, or the one that has been waiting the longest). Provided the queue never becomes empty (i.e., there are always waiting tasks), the waiting time is a power law with exponent -1.5; this behavior is independent of queue length and distribution of priorities (simulations confirm this behavior).
However, the exponent for my software data, and other data, is not -1.5, it is -1. A 2008 paper by Albert-László Barabási (detailed analysis) showed how a modification to the task selection process produces the desired exponent of -1. Each of the tasks currently in the queue is assigned a probability of selection, this probability is proportional to the priority of the corresponding task (i.e., the sum of the priorities/probabilities of all the tasks in the queue is assumed to be constant); task selection is weighted by this probability.
So we have a queueing model whose task waiting time is a power law with an exponent of -1. How well does this model map to software task selection behavior?
One apparent difference between the queueing model and waiting software tasks is that software tasks are assigned to a small number of priorities (e.g., Critical, Major, Minor), while each task in the model queue has a unique priority (otherwise a tie-break rule would have to be specified). In practice, I think that the developers involved do assign unique priorities to tasks.
Why wouldn’t a developer simply select what they consider to be the highest priority task to work on next?
Perhaps each developer does select what they consider to be the highest priority task, but different developers have different opinions about which task has the highest priority. The priority assigned to a task by different developers will have some probability distribution. If task priority assignment by developers is correlated, then the behavior is effectively the same as the queueing model, i.e., the probability component is supplied by different developers having different opinions and the correlation provides a clustering of priorities assigned to each task (i.e., not a uniform distribution).
If this mapping is correct, the task waiting time for a system implemented by one developer should have a power law exponent of -1.5, just like letter writing data.
The number of sprints that a story is assigned to, before being completely implemented, is a power law whose exponent varies around -3. An explanation of this behavior based on priority queues looks possible; we shall see…
The queueing models discussed above are a subset of the field known as bursty dynamics; see the review paper Bursty Human Dynamics for human behavior related aspects.
Most percentages are more than half
Most developers think …
Most editors …
Most programs …
Linguistically most is a quantifier (it’s a proportional quantifier); a word-phrase used to convey information about the number of something, e.g., all, any, lots of, more than half, most, some.
Studies of most have often compared and contrasted it with the phrase more than half; findings include: most has an upper bound (i.e., not all), and more than half has a lower bound (but no upper bound).
A corpus analysis of most (432,830 occurrences) and more than half (4,857 occurrences) found noticeable usage differences. Perhaps the study’s most interesting finding, from a software engineering perspective, was that most tended to be applied to vague and uncountable domains (i.e., there was no expectation that the population of items could be counted), while uses of more than half almost always had a ‘survey results’ interpretation (e.g., supporting data cited as collaboration for 80% of occurrences; uses of most cited data for 19% of occurrences).
Readers will be familiar with software related claims containing the most qualifier, which are actually opinions that are not grounded in substantive numeric data.
When most is used in a numeric based context, what percentage (of a population) is considered to be most (of the population)?
When deciding how to describe a proportion, a writer has the choice of using more than half, most, or another qualifier. Corpus based studies find that the distribution of most has a higher average percentage value than more than half (both are left skewed, with most peaking around 80-85%).
When asked to decide whether a phrase using a qualifier is true/false, with respect to background information (e.g., Given that 55% of the birlers are enciad, is it true that: Most of the birlers are enciad?), do people treat most and more than half as being equivalent?
A study by Denić and Szymanik addressed this question. Subjects (200 took part, with results from 30 were excluded for various reasons) saw a statement involving a made-up object and verb, such as: “55% of the birlers are enciad.” They then saw a sentence containing either most or more than half, that was either upward-entailing (e.g., “More than half of the birlers are enciad.”), or downward-entailing (e.g., “It is not the case that more than half of the birlers are enciad.”); most/more than half and upward/downward entailing creates four possible kinds of sentence. Subjects were asked to respond true/false.
The percentage appearing in the first sentence of the two seen by subjects varied, e.g., “44% of the tiklets are hullaw.”, “12% of the puggles are entand.”, “68% of the plipers are sesare.” The percentage boundary where each subjects’ true/false answer switched was calculated (i.e., the mean of the percentages present in the questions’ each side of true/false boundary; often these values were 46% and 52%, whose average is 49; this is an artefact of the question wording).
The plot below shows the number of subjects whose true/false boundary occurred at a given percentage (code+data):
When asked, the majority of subjects had a 50% boundary for most/more than half+upward/downward. A downward entailment causes some subjects to lower their 50% boundary.
So now we know (subject to replication). Most people are likely to agree that 50% is the boundary for most/more than half, but some people think that the boundary percentage is higher for most.
When asked to write a sentence, percentages above 50% attract more mosts than more than halfs.
Most is preferred when discussing vague and uncountable domains; more than half is used when data is involved.
Parkinson’s law, striving to meet a deadline, or happenstance?
How many minutes past the hour was it, when you stopped working on some software related task?
There are sixty minutes in an hour, so if stop times are random, the probability of finishing at any given minute is 1-in-60. If practice (based on the 200k+ time records in the CESAW dataset) the probability of stopping on the hour is 1-in-40, and for stopping on the half-hour is 1-in-48.
Why are developers more likely to stop working on a task, on the hour or half-hour?
Is this a case of Parkinson’s law, or are developers striving to complete a task within a specified time, or are they stopping because a scheduled activity takes priority?
The plot below shows the number of times (y-axis) work on a task stopped on a given minute past the hour (x-axis), for 16 different software projects (project number in blue, with top 10 numbers in red, code+data):
Some projects have peaks at 50, 55, or thereabouts. Perhaps people are stopping because they have a meeting to attend, and a peak is visible because the project had lots of meetings, or no peak was visible because the project had few meetings. Some projects have a peak at 28 or 29, which might be some kind of time synchronization issue.
Is it possible to analyze the distribution of end minutes to reasonably infer developer project behavior, e.g., Parkinson’s law, striving to finish by a given time, or just not watching the clock?
An expected distribution pattern for both Parkinson’s law, and striving to complete, is a sharp decline of work stops after a reference time, e.g., end of an hour (this pattern is present in around ten of the projects plotted). A sharp increase in work stops prior to a reference time could also apply for both behaviors; stopping to switch to other work adds ‘noise’ to the distribution.
The CESAW data is organized by project, not developer, i.e., it does not list everything a developer did during the day. It is possible that end-of-hour work stops are driven by the need to synchronize with non-project activities, i.e., no Parkinson’s law or striving to complete.
In practice, some developers may sometimes follow Parkinson’s law, other times strive to complete, and other times not watch the clock. If models capable of separating out the behaviors were available, they might only be viable at the individual level.
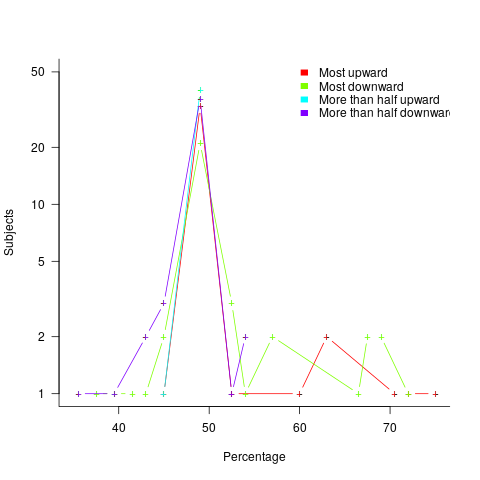
Stop time equals start time plus work duration. If people choose a round number for the amount of work time, there is likely to be some correlation between start/end minutes past the hour. The plot below shows heat maps for start fraction of hour (y-axis) against end fraction of hour (x-axis) for four projects (code+data):
Work durations that are exact multiples of an hour appear along the main diagonal, with zero/zero being the most common start/end pair (at 4% over all projects, with 0.02% expected for random start/end times). Other diagonal lines come from work durations that include a fraction of an hour, e.g., 30-minutes and 20-minutes.
For most work periods, the start minute occurs before the end minute, i.e., the work period does not cross an hour boundary.
What can be learned from this analysis?
The main takeaway is that there is a small bias for work start/end times to occur on the hour or half-hour, and other activities (e.g., meetings) cause ongoing work to be interrupted. Not exactly news.
More interesting ideas and suggestions welcome.
The Approximate Number System and software estimating
The ability to perform simple numeric operations can improve the fitness of a creature (e.g., being able to select which branch contains the most fruit), increasing the likelihood of it having offspring. Studies have found that a wide variety of creatures have a brain subsystem known as the Approximate Number System (ANS).
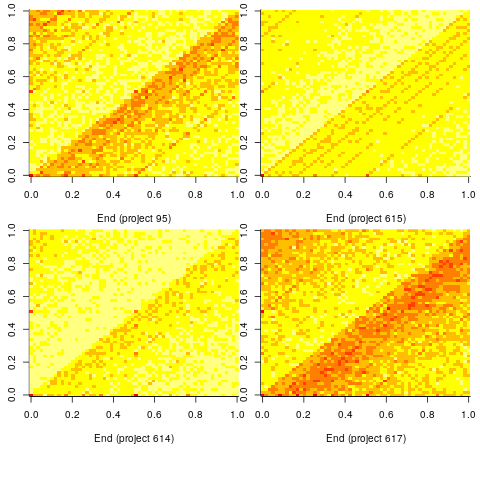
A study by Mechner rewarded rats with food, if they pressed a lever N times (with N taking one of the values 4, 8, 12 or 16), followed by pressing a second lever. The plot below shows the number of lever presses made before pressing the second lever, for a given required N; it suggests that the subject rat is making use of an approximate number system (code+data):
Humans have a second system for representing numbers, which is capable of exact representation, it is language. The Number Sense by Stanislas Dehaene was on my list of Christmas books for 2011.
One method used to study the interface between the two language systems, available to humans, involves subjects estimating the number of dots in a briefly presented image. While reading about one such study, I noticed that some of the plots showed patterns similar to the patterns seen in plots of software estimate/actual data. I emailed the lead author, Véronique Izard, who kindly sent me a copy of the experimental data.
The patterns I was hoping to see are those invariably seen in software effort estimation data, e.g., a power law relationship between actual/estimate, consistent over/under estimation by individuals, and frequent use of round numbers.
Psychologists reading this post may be under the impression that estimating the time taken to implement some functionality, in software, is a relatively accurate process. In practice, for short tasks (i.e., under a day or two) the time needed to form a more accurate estimate makes a good-enough estimate a cost-effective option.
This Izard and Dehaene study involved two experiments. In the first experiment, an image containing between 1 and 100 dots was flashed on the screen for 100ms, and subjects then had to type the estimated number of dots. Each of the six subjects participated in five sessions of 600 trials, with each session lasting about one hour; every number of dots between 1 and 100 was seen 30 times by each subject (for one subject the data contains 1,783 responses, other subjects gave 3,000 responses). Subjects were free to type any value as their estimate.
These kinds of studies have consistently found that subject accuracy is very poor (hardly surprising, given that subjects are not provided with any feedback to help calibrate their estimates). But since researchers are interested in patterns that might be present in the errors, very low accuracy is not an issue.
The plot below shows stimulus (number of dots shown) against subject response, with green line showing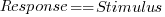 
, and red line a fitted regression model having the form 
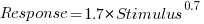(which explains just over 70% of the variance; code+data):
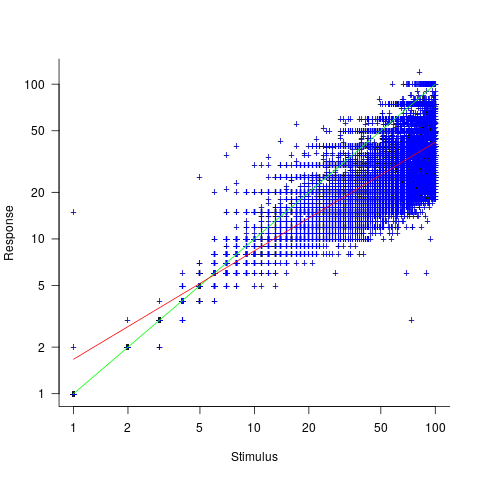
Just like software estimates, there is a good fit to a power law, and the only difference in accuracy performance is that software estimates tend not to be so skewed towards underestimating (i.e., there are a lot more low accuracy overestimates).
Adding subjectID to the model gives: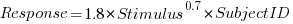 
, with 
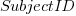varying between 0.65 and 1.57; more than a factor of two difference between subjects (this model explains just under 90% of the variance). This is a smaller range than the software estimation data, but with only six subjects there was less chance of a wider variation (code+data).
The software estimation data finds shows that accuracy does not improve with practice. The experimental subjects were not given any feedback, and would not be expected to improve, but does the strain of answering so many questions cause them to get worse? Adding trial number to the model suggests a 12% increase in underestimation, over 600 trials. However, adding an interaction with SubjectID shows that the performance of two subjects remains unchanged, while two subjects experience a 23% increase in underestimation.
The plot below shows the number of times each response was given, combining all subjects, with commonly given responses in red (code+data):
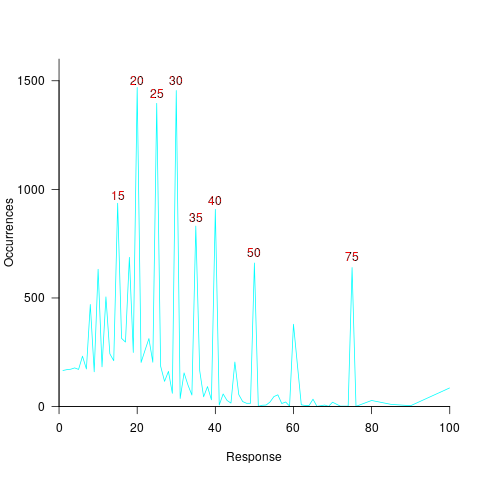
The commonly occurring values that appear in software estimation data are structured as fractions of units of time, e.g., 0.5 hours, or 1 hour or 1 day (appearing in the data as 7 hours). The only structure available to experimental subjects was subdivisions of powers of 10 (i.e., 10 and 100).
Analysing the responses by subject shows that each subject had their own set of preferred round numbers.
To summarize: The results from an experiment investigating the interface between the two human number systems contains three patterns seen in software estimation data, i.e., power law relationship between actual and estimate, individual differences in over/underestimating, and extensive use of round numbers.
Izard’s second experiment limited response values to prespecified values (i.e., one to 10 and multiples of 10), and gave a calibration example after each block of 46 trials. The calibration example improved performance, and the use of round numbers as prespecified response values had the effect of removing spikes from the response counts (which were relatively smooth; code+data)).
We now have circumstantial evidence that software developers are using the Approximate Number System when making software estimates. We will have to wait for brain images from a developer in an MRI scanner, while estimating a software task, to obtain more concrete proof that the ANS is involved in the process. That is, are the areas of the brain thought to be involved in the ANS (e.g., the intraparietal sulcus) active during software estimation?
What is known about software effort estimation in 2021
What do we know about software effort estimation, based on evidence?
The few publicly available datasets (e.g., SiP, CESAW, and Renzo) involve (mostly) individuals estimating short duration tasks (i.e., rarely more than a few hours). There are other tiny datasets, which are mostly used to do fake research. The patterns found across these datasets include:
- developers often use round-numbers,
- the equation: 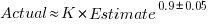, where
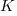is a constant that varies between projects, often explains around 50% of the variance present in the data. This equation shows that developers under-estimate short tasks and over-estimate long tasks. The exponent, 
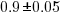, applies across most projects in the data, - individuals tend to either consistently over or under estimate,
- developer estimation accuracy does not change with practice. Possible reasons for this include: variability in the world prevents more accurate estimates, developers choose to spend their learning resources on other topics.
Does social loafing have an impact on actual effort? The data needed to answer this question is currently not available (the available data mostly involves people working on their own).
When working on a task, do developers follow Parkinson’s law or do they strive to meet targets?
The following plot suggests that one or the other, or both are true (data):
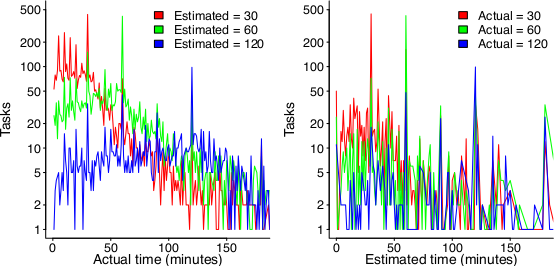
On the left: Each colored lines shows the number of tasks having a given actual implementation time, when they were estimated to take 30, 60 or 120 minutes (the right plot reverses the role of estimate/actual). Many of the spikes in the task counts are at round numbers, suggesting that the developer has fixated on a time to finish and is either taking it easy or striving to hit it. The problem is distinguishing them mathematically; suggestions welcome.
None of these patterns of behavior appear to be software specific. They all look like generic human behaviors. I have started emailing researchers working on project analytics in other domains, asking for data (no luck so far).
Other patterns may be present for many projects in the existing data, we have to wait for somebody to ask the right question (if one exists).
It is also possible that the existing data has some unusual characteristics that don’t apply to most projects. We won’t know until data on many more projects becomes available.
Effort estimation’s inaccurate past and the way forward
Almost since people started building software systems, effort estimation has been a hot topic for researchers.
Effort estimation models are necessarily driven by the available data (the Putnam model is one of few whose theory is based on more than arm waving). General information about source code can often be obtained (e.g., size in lines of code), and before package software and open source, software with roughly the same functionality was being implemented in lots of organizations.
Estimation models based on source code characteristics proliferated, e.g., COCOMO. What these models overlooked was human variability in implementing the same functionality (a standard deviation that is 25% of the actual size is going to introduce a lot of uncertainty into any effort estimate), along with the more obvious assumption that effort was closely tied to source code characteristics.
The advent of high-tech clueless button pushing machine learning created a resurgence of new effort estimation models; actually they are estimation adjustment models, because they require an initial estimate as one of the input variables. Creating a machine learned model requires a list of estimated/actual values, along with any other available information, to build a mapping function.
The sparseness of the data to learn from (at most a few hundred observations of half-a-dozen measured variables, and usually less) has not prevented a stream of puffed-up publications making all kinds of unfounded claims.
Until a few years ago the available public estimation data did not include any information about who made the estimate. Once estimation data contained the information needed to distinguish the different people making estimates, the uncertainty introduced by human variability was revealed (some consistently underestimating, others consistently overestimating, with 25% difference between two estimators being common, and a factor of two difference between some pairs of estimators).
How much accuracy is it realistic to expect with effort estimates?
At the moment we don’t have enough information on the software development process to be able to create a realistic model; without a realistic model of the development process, it’s a waste of time complaining about the availability of information to feed into a model.
I think a project simulation model is the only technique capable of creating a good enough model for use in industry; something like Abdel-Hamid’s tour de force PhD thesis (he also ignores my emails).
We are still in the early stages of finding out the components that need to be fitted together to build a model of software development, e.g., round numbers.
Even if all attempts to build such a model fail, there will be payback from a better understanding of the development process.
Recent Comments