Distribution of program sizes
Program size, in lines of code (LOC), used to be a topic of conversation among developers and managers. Program size is an issue when computer memory is measured in kilobytes. Large programs would be organized into overlays such that only small subsets needed to be held in memory at any time, i.e., programmer defined memory management.
Management used program size as a proxy for implementation effort/cost. Because size was a topic of conversation, it was possible to ask around to obtain a selection of values for the size of programs with similar functionality (accurate actual implementation costs were/are rarely available via the grapevine, but developers were/are always happy to talk about how small/large their programs were/are). These days, estimating LOC prior to implementation may appear more scientific, but I doubt it’s more accurate.
Once computers containing megabytes of memory became widespread, and the use of third-party libraries continued to grow, program size became a niche topic of conversation.
The size of some operating systems has become an occasional topic of conversation; it wasn’t previously because mainframe/mini computer manufacturers didn’t want customers talking about how much of their expensive memory was taken up by the OS. The size of Microsoft Windows leaked out and the Linux kernel is a topic of research.
Discussions around size have moved on from individual programs to the amount of space taken up by an installed application suite. Today, program size can be a rounding error compared to data files, extensions and add-ons.
Researchers have also moved on; repository size, in LOC/packages, is what now gets reported.
For those who are interested in program size; what is the distribution of program sizes? How many LOC are needed for a program to be above 50%, or in the top 95%?
Recent data on the size of individual programs is surprisingly hard to find, given how often LOC values appear in print. The one dataset I found is from the paper Empirical analysis of the relationship between CC and SLOC in a large corpus of Java methods and C functions, which is derived from the 2010’ish Sourcerer corpus of 13,103 Java projects (each of which I assume contains one program). The plot below shows the LOC (red) and methods (blue/green) for each program, in ascending order, along with values at various percentage points (code+data):
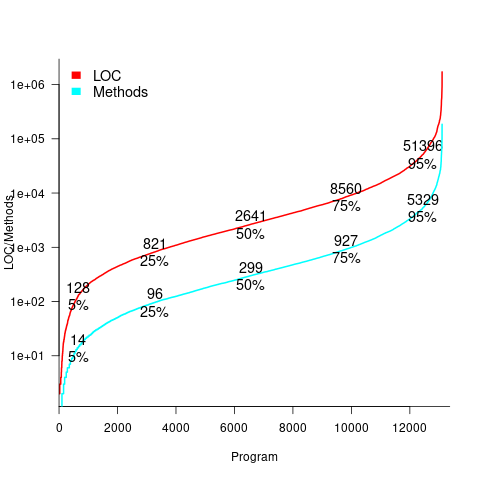
The size of Java programs is very likely to have increased since 2010. How much have grown? I don’t know.
What about the size of programs written in other languages?
I expect Python program size to be smaller, because the huge number of available package removes the need to implement a myriad of boilerplate functionality.
I expect C program size to be larger, both because of the smaller library ecosystem and because C programs tend to be older (programs rarely shrink with age).
Quantity of source in a given language
How much source code exists in a particular language?
Traditionally, indicators of the quantity of source in a language is the number of people making a living working on software written in the language. Job adverts are a proxy for the number of people employed to write/support programs implemented in a language (i.e., number of times a language is specified in the text of an advert), another proxy used to be the financial wellbeing of compiler vendors (many years ago, Open source compilers drove most companies out of the business of selling compilers).
Current job adverts are a measure of the code that likely to be worked now and in the near future. While Cobol dominated the job adverts decades ago, it is only occasionally seen today, suggesting that a lot of Cobol source is no longer actively used.
There now exists a huge quantity of Open source, and it has permeated into all the major, and many minor, software ecosystems. As a measure of all existing source code, how representative is Open source?
The Software Heritage’s mission statement “… is to collect, preserve, and share all software that is publicly available in source code form.” With over 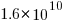 files, as of July 2023 it is the largest available collection of Open source, and furthermore the BigCode project has collated this source into 658 constituent languages, known the Stack version 2.
files, as of July 2023 it is the largest available collection of Open source, and furthermore the BigCode project has collated this source into 658 constituent languages, known the Stack version 2.
To be representative of all existing source code, the Stack v2 would need to contain a representative sample of source written in all the languages that have been used to implement a non-trivial quantity of code. The plot below shows the number of source files assumed to be from a given year, storage by the Software Heritage; green lines are fitted exponentials (code+data):
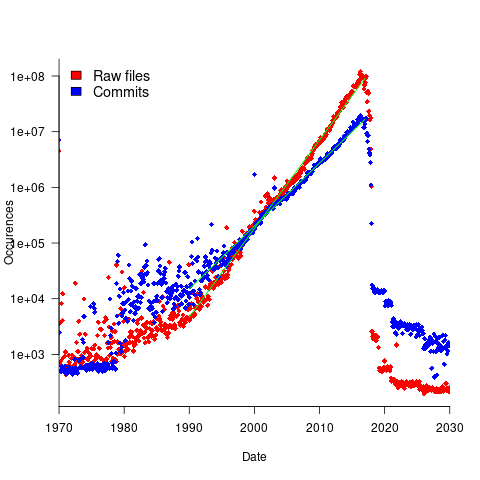
Less Open source was written in years gone by because there were fewer developers writing code, and code tends to get lost.
The Wikipedia list of programming languages currently contains links to articles on 682 languages, although some entries do appear to stretch the definition of programming language, e.g., Geometric Description Language. The Stack v2 contains code in 658 languages. However, even the broadest definition of programming language would not include some of the entries, e.g., Vim Help File. There are 176 language names shared between lists (around 27%; code+data).
Wikipedia languages not contained in Stack v2 include dialects of Basic, C, Lisp, Pascal, and shell, along with languages I recognised. Stack v2 languages not contained in the Wikipedia list include a variety of build and configuration files, names I did not recognise and what looked like documentation and data files.
Stack v2 has a broad brush approach to language classification. There is only one Pascal (perhaps the most widely used language in the early days of the IBM PC, Turbo Pascal, does not get a mention, and neither does UCSD Pascal), and assembler languages can vary a lot between cpus (Stack v2 lists: Assembly, Motorola 68K Assembly, Parrot Assembly, WebAssembly, Unix Assembly).
The Online Historical Encyclopaedia of Programming Languages lists information on 8,945 languages. Most of these probably got no further than being implemented in themselves by the language designer (often for a PhD thesis).
The Stack v2’s definition of a non-trivial quantity is at least 1,000 files having a given filename suffix, e.g., .cpp denoting C++ source. I can understand that this limit might exclude some niche languages from long ago (e.g., Coral 66), but why isn’t there any Algol 60 source?
I suspect that many ‘earlier’ languages are not included because the automated source submission process requires that the code be accessible via one of five version control systems. A lot of older source is stored in tar/zip files, accessed via ftp directories or personal web pages. Software Heritage’s Collect and Curate Legacy Code does not yet appear to provide a process for submitting source available in these forms.
While I think that Open source code has the same language usage characteristics as Closed source, I continue to meet people who question this assumption. I doubt that the question will ever get a definitive answer, not least because of an unwillingness to invest the resources needed to do a large sample comparison.
I would expect there to be at least 100 times as much Closed source as Open source, if only because there are a lot more people writing Closed source.
Obtaining source code for training LLMs
Training a large language model to be a coding assistant requires huge amounts of source code.
Github is a very well known publicly available repository of code, and various sites have created substantial collections of GitHub repos, e.g., GitTorrent, and Google’s BigQuery. Since 2017 the Software Heritage has been amassing the world’s source code, and now looks like it will become the default site for those seeking LLM source code training data. The benefits of using the Software_Heritage, include:
- deduplication at the file level for free. Files are organized using a cryptographic hash of their contents (i.e., a Merkle tree), which is user visible. GitHub may deduplicate internally, but the user visible data structure is based on individual repositories. One study found that 70% of code on GitHub are clones. Deduplication has been a major housekeeping task when creating a source code training dataset.
A single space character or newline is enough to cause a cryptographic hash to change and a file to be treated as different. Studies of file contents has found them differing by the presence/absence of a license at the start of the file, and other non-consequential differences. The LLM training dataset “The Stack v2” has further deduplicated the Software Heritage dataset, removing over 50% of files,
- accessed using AWS. The 11TiB of data can be bulk downloaded from the S3 bucket s3://softwareheritage/graph/. An Amazon Athena hosted version of the dataset can be queried using the Presto distributed SQL engine (filename suffix could be used to extract files likely to contain source in particular languages). Amazon also have an Azure Databricks hosted version.
Suggestions for the best way of accessing this data, for LLM training, welcome,
- Software_Heritage hosts more code than GitHub, although measurements from late 2021 suggests that at the time, over 95% originated on GitHub.
StarCoder2, released at the end of February, is an open weights model trained in partnership with the Software Heritage (a year ago, version 1 of StarCoder was trained using an order of magnitude less source).
How much source is available via the Software Heritage?
As of July 2023 the site hosted 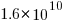 files.
files.
Let’s assume 64 lines per file, and 26 non-whitespace characters per line, giving 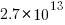 non-whitespace characters. How many tokens is this?
non-whitespace characters. How many tokens is this?
The most common statement is assignment, which typically contains 4 language tokens (e.g., a = b ; ). There is an exponential decline in language tokens per line (Fig 770.17). The question is how many LLM tokens per computer language identifier, which tend to be abbreviated; I have no idea how these map to LLM tokens.
Assuming 10 LLM tokens per line, we get: 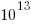 LLM tokens; this is 2.7 non-whitespace characters per token, which feels about right.
LLM tokens; this is 2.7 non-whitespace characters per token, which feels about right.
The Stack v2 Hugging Face page lists the deduplicated dataset as containing 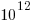 tokens. However, they only include files in the main branch (the Software Heritage dataset includes files containing branches and commits), and the total number of files in the full Stack v2 dataset is
tokens. However, they only include files in the main branch (the Software Heritage dataset includes files containing branches and commits), and the total number of files in the full Stack v2 dataset is 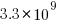 , with the deduped training dataset containing
, with the deduped training dataset containing 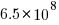 files (they do not train using copyleft files, which are approximately 20-25% of the files on GitHub).
files (they do not train using copyleft files, which are approximately 20-25% of the files on GitHub).
My calculation probably overestimated the number of tokens on a line. LLM’s specifically trained on source code have tokenisers optimized for the characteristics of code, e.g., allowing tokens to span whitespace to allow for idioms such as import numpy as np to be treated as single tokens.
Given the exponential growth of files available on the Software Heritage, it is possible that several orders of magnitude more tokens will eventually become available.
Licensing, in the form of the GPL, is a complication that hangs over the use of some public source code (maybe 25%). An ongoing class-action suit will likely take years to resolve, and it’s possible that model training will have improved to the extent that any loss of GPL’d code will not seriously impact model performance:
- When source is licensed under the GNU General Public License, do models that use it during training have themselves to be released under a GPL license? In November 2022 a class-action lawsuit was filed, challenging the legality of GitHub Copilot and related OpenAI products. This case has yet to reach jury trial, and after that there will no doubt be appeals. The resolution is years in the future,
- if the plaintiffs win, with models trained using GPL’d code required to release the weights under a GPL license. The different source files used to build a project sometimes have different, incompatible, Open source licenses. LLM training does not require complete sets of project source files, so the presence of GPL’d source is not contagious within a project. If the same file appears with different licenses, one of which is the GPL, the simplest option may be to exclude it. One study found the GPL-3 license present under 2,871 different filenames.
Given that around 50% of GitHub repos don’t specify any license, and around 30% specify an MIT license, not using GPL’d code for training does not look like it will affect the training of general coding models. However, these models will have problems dealing with issues that require interfacing to GPL’d code.
Sampling error in software engineering
In the physical sciences, measurement error occurs because of accuracy limits on the device used to make the measurement and the interpretation of the data by the person doing the measurement.
In software engineering, some measurements appear to be error free. For instance, lines of code is a discrete value that is easily counted. While some people don’t include blank lines and/or comments, the choice of what to count does not prevent an exact count being made.
In physics, the behavior of particular elements does not depend on the identity of which atoms are measured, while in software the behavior of programs written to the same specification can have different characteristics, e.g., lines of code.
For instance, each implementation of the 3n+1 problem will contain some number of LOC, with other implementations often containing a different number of LOC. The plot below shows the distribution of LOC for 6,301 implementations of 3n+1 (code and data):

Each program implementing the 3n+1 problem is one sample from the population of programs implementing the 3n+1 specification. Different people are likely to implement different programs, and the same person may create different implementations at different times.
Sampling error occurs when the characteristics of a sample are used to infer characteristics about the population from which the sample was drawn.
How might sampling error affect the results of data analysis?
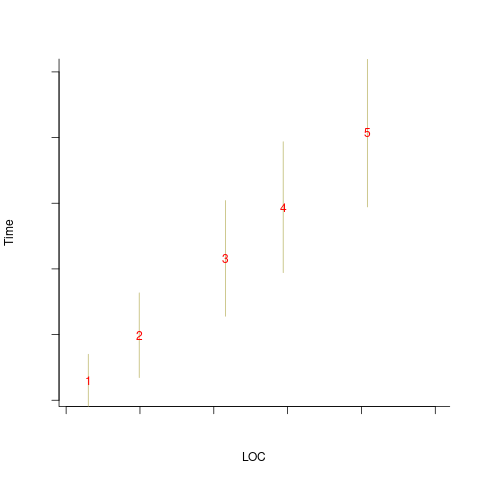
An example, using made-up values: Assume that two sets of sample measurements are made of the time taken to implement five different specifications, along with the lines of code contained in the implementations (in the same language). In the plot below, the yellow circles show a range of likely implementation measurements for each of the five specifications. The green dots, one for each specification, are measurements of one sample of programs implementing each specification; the blue dots are a second sample of programs (code):

The green and blue lines show the ordinary least squares regression model fitted to each sample. The different samples selected from the five populations has produced what appears to be slightly different models. How significant is this difference in the fitted models?
The grey line denotes where LOC is proportional to implementation time, which is one hypothesis of software project progress. The green line sample implies that LOC growth decreases as implementation time increases, while the blue line sample implies the reverse (both have been proposed as hypotheses of software project progress).
The difference in this example is important because the models fitted to the samples straddle the demarcation line between alternative theories of software project development.
A larger sample may not produce a more accurate model; a previous post analyses such a case. The example above shows a symmetric uniformly distributed population because that is the easiest to plot. In practice, populations distributions are likely to be asymmetric and irregular, e.g., measured time may be rounded to the nearest appropriate unit.
The mathematics underpinning OLS assumes that there is no error in the explanatory variables (LOC in the above plot), and that all the error is concentrated in the response variable (Time in the above plot). When there is a non-trivial sample error, or measurement error, OLS is not the appropriate technique to use to fit a regression model. The plot below shows the sample error that is assumed by OLS (code):
When there is a non-trivial error in the explanatory variable (LOC in this example), the appropriate technique for fitting a regression model is errors-in-variables regression.
Building an errors-in-variables regression model requires values for the error in the variables appearing in the equation to be fitted. Obtaining these values can be very difficult (Deming regression is a fitting technique based on the ratio of the errors).
In the above example, what is the likely variability in the implementation time and LOC, for a given specification? The limited data on the LOC contained in multiple implementations of the same specification suggests that the standard deviation of the LOC across implementations of the same specification is around 25% of the mean.
Learning researchers have run experiments where each subject performs the same task multiple times. Performance improves with practice, which makes it difficult to calculate the likely variability in the first-time performance.
My book: Evidence-based software engineering recommends using SIMEX to fit errors-in-variables models (section 11.2.3). This technique takes a model fitted using existing methods (allowing a wide range of models to be fitted), and then refits the model created based on the estimated error in one or more explanatory variables (no need to estimate an error in the response variable, the technique makes use of the value from the initial fit).
A surprising retrospective task estimation dataset
When estimating the time needed to implement a task, the time previously needed to implement similar tasks provides useful guidance. The implementation time for these previous tasks may itself be estimated, because the actual time was not measured or this information is currently unavailable.
How accurate are developer time estimates of previously completed tasks?
I am not aware of any software related dataset of estimates of previously completed tasks (it’s hard enough finding datasets containing information on the actual implementation time). However, I recently found the paper Dynamics of retrospective timing: A big data approach by Balcı, Ünübol, Grondin, Sayar, van Wassenhove, and Wittmann. The data analysed comes from a survey questionnaire, where 24,494 people estimated the how much time they had spent answering the questions, along with recording the current time at the start/end of the questionnaire. The supplementary data is in MATLAB format, and is also available as a csv file in the Blursday database (i.e., RT_Datasets).
Some of the behavior patterns seen in software engineering estimates appear to be general human characteristics, e.g., use of round numbers. An analysis of the estimation performance of a wide sample of the general population could help separate out characteristics that are specific to software engineering and those that apply to the general population.
The following table shows the percentage of answers giving a particular Estimate and Actual time, in minutes. Over 60% of the estimates are round numbers. Actual times are likely to be round numbers because people often give a round number when asked the time (code+data):
Minutes Estimate Actual
20 18% 8.5%
15 15% 5.3%
30 12% 7.6%
25 10% 6.2%
10 7.7% 2.1% |
I was surprised to see that the authors had fitted a regression model with the Actual time as the explanatory variable and the Estimate as the response variable. The estimation models I have fitted always have the roles of these two variables reversed. More of this role reversal difference below.
The equation fitted to the data by the authors is (they use the term Elapsed, for consistency with other blog articles I continue to use Actual; code+data):
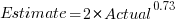
This equation says that, on average, for shorter Actual times the Estimate is higher than the Actual, while for longer Actual times the average Estimate is lower.
Switching the roles of the variables, I expected to see a fitted model whose coefficients are somewhat similar to the algebraically transformed version of this equation, i.e., 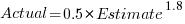 . At the very least, I expected the exponent to be greater than one.
. At the very least, I expected the exponent to be greater than one.
Surprisingly, the equation fitted with the variables roles reversed is very similar, i.e., the equations are the opposite of each other:
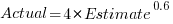
This equation says that, on average, for shorter Estimate times the Actual time is higher than the Estimate, while for longer Estimate times the average Actual is lower, i.e., the opposite behavior specifie dby the earlier equation.
I spent some time trying to understand how it was possible for data to be fitted such that (x ~ y) == (y ~ x), even posting a question to Cross Validated. I might, in a future post, discuss the statistical issues behind this behavior.
So why did the authors of this paper treat Actual as an explanatory variable?
After a flurry of emails with the lead author, Fuat Balcı (who was very responsive to my questions), where we both doubled checked the code/data and what we thought was going on, Fuat answered that (quoted with permission):
“The objective duration is the elapsed time (noted by the experimenter based on a clock reading), and the estimate is the participant’s response. According to the psychophysical approach the mapping between objective and subjective time can be defined by regressing the subjective estimates of the participants on the objective duration noted by the experimenter. Thus, if your research question is how human’s retrospective experience of time changes with the duration of events (e.g., biases in time judgments), the y-axis should be the participant’s response and the x-axis should be the actual duration.”
This approach has a logic to it, and is consistent with the regression modelling done by other researchers who study retrospective time estimation.
So which modelling approach is correct, and are people overestimating or underestimating shorter actual time durations?
Going back to basics, the structure of this experiment does not produce data that meets one of the requirements of the statistical technique we are both using (ordinary least squares) to fit a regression model. To understand why ordinary least squares, OLS, is not applicable to this data, it’s necessary to delve into a technical detail about the mathematics of what OLS does.
The equation actually fitted by OLS is: 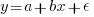 , where
, where  is an error term (i.e., ‘noise’ caused by all the effects other than
is an error term (i.e., ‘noise’ caused by all the effects other than  ). The value of
). The value of  is assumed to be exact, i.e., not contain any ‘noise’.
is assumed to be exact, i.e., not contain any ‘noise’.
Usually, in a retrospective time estimation experiment, subjects hear, for instance, a sound whose duration is decided in advance by the experimenter; subjects estimate how long each sound lasted. In this experimental format, it makes sense for the Actual time to appear on the right-hand-side as an explanatory variable and for the Estimate response variable on the left-hand-side.
However, for the questionnaire timing data, both the Estimate and Actual time are decided by the person giving the answers. There is no experimenter controlling one of the values. Both the Estimate and Actual values contain ‘noise’. For instance, on a different day a person may have taken more/less time to actually answer the questionnaire, or provided a different estimate of the time taken.
The correct regression fitting technique to use is errors-in-variables. An errors-in-variables regression fits the equation: 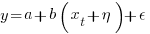 , where:
, where: 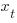 is the true value of
is the true value of  and
and 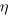 is its associated error. A selection of packages are available for fitting a variety of errors-in-variables models.
is its associated error. A selection of packages are available for fitting a variety of errors-in-variables models.
I regularly see OLS used in software engineering papers (including mine) where errors-in-variables is the technically correct technique to use. Researchers are either unaware of the error issues or assuming that the difference is not important. The few times I have fitted an errors-in-variables model, the fitted coefficients have not been much different from those fitted by an OLS model; for this dataset the coefficient difference is obviously important.
The complication with building an errors-in-variables model is that values need to be specified for the error terms 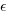 and
and 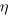 . With OLS the value of
. With OLS the value of 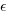 is produced as part of the fitting process.
is produced as part of the fitting process.
How might the required error values be calculated?
If some subjects round reported start/stop times, there may not be any variation in reported Actual time, or it may jump around in 5-minute increments depending on the position of the minute hand on the clock.
Learning researchers have run experiments where each subject performs the same task multiple times. Performance improves with practice, which makes it difficult to calculate the likely variability in the first-time performance. If we assume that performance is skill based, the standard deviation of all the subjects completing within a given timeframe could be used to calculate an error term.
With 60% of Estimates being round numbers, there might not be any variation for many people, or perhaps the answer given will change to a different round number. There is Estimate data for different, future tasks, and a small amount of data for the same future tasks. There is data from many retrospective studies using very short time intervals (e.g., tens of seconds), which might be applicable.
We could simply assume that the same amount of error is present in each variable. Deming regression is an errors-in-variables technique that supports this approach, and does not require any error values to be specified. The following equations have been fitted using Deming regression (code+data):
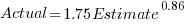
and
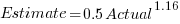
While these two equations are consistent with each other, we don’t know if the assumption of equal errors in both variables is realistic.
What next?
Hopefully it will be possible to work out reasonable error values for the Actual/Estimate times. Fitting a model using these values will tell us wether any over/underestimating is occurring, and the associated span of time durations.
I also need to revisit the analysis of software task estimation times.
Workshop on data analysis for software developers
I’m teaching a workshop on data analysis for software engineers on 22 June. The workshop is organized by the British Computer Society’s SPA specialist group, and can be attended remotely.
Why is there a small registration charge (between £2 and £15)? Typically, 30% to 50% of those registered for a free event actually turn up. It is very frustrating when all the places are taken, people are turned away, and then only half those registered turn up. We decided to charge a minimal amount to deter the uncommitted, and include lunch. Why the variable pricing? The BCS have a rule that members have to get a discount, and HMRC does not allow paid+free options (I suspect this has more to do with the software the BCS are using).
It’s a hands-on workshop that aims to get people up and running with practical data analysis. As always, my data analysis hammer of choice is regression analysis.
A few things are being updated since I last gave this workshop?
While my completed book Evidence-based Software Engineering was not available when the last workshop was given, the second half containing the introductory statistics material was available for download. There has not been any major changes to the statistical material in this second half.
The one new statistical observation I plan to highlight is that in software engineering, there is a lot of data that does not have a normal distribution. Many data analysis are aimed at the social sciences (the biggest market), and they frequently just assume that all the data is normally distributed; software engineering data is different.
For a very long time I have known that most developers/managers do not collect and analyse measurements of their development processes. However, I had underestimated ‘most’, which I now think is at least 99%.
Given the motivation, developers/managers would measure and analyse processes. I plan to update the material to have a motivational theme, along with illustrating the statistical points being made. The purpose of the motivational examples is to give attendees something to take back and show their managers/coworkers: Look, we can find out where all our money/time is being wasted. I assume that attendees are already interested in analysing software engineering data (why else would they be spending a Saturday at the workshop).
I have come up with a great way of showing how many of software engineering’s cited ‘facts’ are simply folklore derived from repeating opinions from papers published long ago (or derived from pitifully small amounts of data). The workshop is hands-on, with attendees individually working through examples. The plan is for examples to be based on the data behind some of these ‘facts’, e.g., Halstead & McCabe metrics, and COCOMO.
Tips, and suggestions for topics to discuss welcome.
Survey papers: LLMs will restore some level of usefulness
Scientific papers are like soap operas, in that understanding them requires readers to have some degree of familiarity with the ongoing plot.
How can people new to an opera quickly get up to speed with the ongoing story lines, without reading hundreds of papers?
The survey paper is intended to be the answer to this question. Traditionally written by an established researcher in the field, the 100+ pages aim to be an authoritative overview of the progress and setbacks of research on a particular topic within the last 5/10/15 years (depending on the rate/lack of progress since the last major survey paper).
These days research papers are often written by PhD students, with the professor doing the supervising, and getting their name tacked on to the end of the list of authors (professors can spend more time writing grant applications than writing research papers). Writing a single 100+ page survey paper is not a cost-effective use of an experienced person’s time, given the pressure to pump out papers, even when the ACM Computing Surveys is one of the highest ranked journals in computing. The short lifecycle of fields driven by the next fashionable topic is another disincentive.
Given the incentives, why are survey papers still being published?
In software engineering there are now two kinds of survey papers: 1) the traditional kind, written by people who see it as a service, or are not on the publish/perish treadmill, or early stage researchers surveying a niche topic, 2) PhD students using what we now call a Large language model summary approach, soon to be replaced by real LLMs.
So-called survey papers (at least in software engineering) are now regularly being written by members of the intended audience of traditional survey papers, i.e., PhD students who are new to the field and want a map of the territory showing the routes to the frontiers.
How does a person who knows almost nothing about a field write a (20-40 page, rarely 100+) survey paper about it?
A survey is based on the list of all the appropriate papers. In theory, appropriate papers have to meet some quality criteria, e.g., be published in a reputable journal/conference/blog. In practice, the list is created by searching various academic publication search engines (e.g., web of science, or the ACM digital library) using a targeted regular expression; for instance:
(agile OR waterfall OR software OR "story points" OR "story point" OR "user stories" OR "function points" OR "planning poker" OR "pomodoros" OR "use case" OR "source code" OR "DORA metrics" OR scrum) (predict OR prediction OR quantify OR dataset OR schedule OR lifecycle OR "life cycle" OR estimate OR estimates OR estimating OR estimation OR estimated OR #noestimates OR "evidence" OR empirical OR evolution OR ecosystems OR cognitive OR economics OR reliability OR metrics OR experiment) |
The list of papers returned may be filtered further, depending on how many there are (a hundred or two does not look too lightweight, and does not require an excessive amount of work).
Next, what to say about these papers, and how many of them actually need to be read?
The bottom of the barrel, vacant ideas, survey paper tabulates easily calculated metrics (e.g., number of papers per year, number of authors per paper, clusters of keywords), and babble on about paper selection criteria, keyword growth and diversity, and more research is needed.
For a survey paper to appear in a layer above the vacant ideas level, the authors have to process some amount of the paper contents. The paper A Systematic Literature Review on Reasons and Approaches for Accurate Effort Estimations in Agile by Pasuksmit, Thongtanunam, and Karunasekera is a recent example of one such survey. The search criteria returned 519 papers, of which 82 were selected for inclusion, i.e., cited. The first 10, of the 42 pages, covered the selection process and the process used to answer the two research questions; RQ1: What are the discovered reasons for inaccurate estimations in Agile iterative development? and RQ2: What are the approaches proposed to improve effort estimation in Agile iterative development?
The main answers to the research questions appeared in: 1) tables which listed attributes relating to the question and the papers that had something to say about that attribute, and 2) sections containing a few paragraphs highlighting various points made by papers about some attribute.
My primary interest was Table 11, which listed the papers/dataset used. A few were new to me, but unfortunately all confidential.
A survey can only be as good as the papers it is based on. The regular expression approach can miss important papers and include unimportant papers. The Pasuksmit et al paper only included one paper by the leading researcher in Agile effort estimation, and included papers that I wouldn’t waste disk space on a pdf file.
I would not recommend these ‘LLM’ style surveys to newcomers to a field. They don’t connect the lines of research, call out the successes/failures, and they don’t provide a map of the territory.
The readership of these survey papers are the experienced researchers, who will scan the list of cited papers looking for anything they might have missed.
I’m not expecting LLMs to be capable of producing experienced professor level survey papers any time soon. In a year or two, LLMs will surely be doing a better job than PhD students.
Chinchilla Scaling: A replication using the pdf
The paper Chinchilla Scaling: A replication attempt by Besiroglu, Erdil, Barnett, and You caught my attention. Not only a replication, but on the first page there is the enticing heading of section 2, “Extracting data from Hoffmann et al.’s Figure 4”. Long time readers will know of my interest in extracting data from pdfs and images.
This replication found errors in the original analysis, and I, in turn, found errors in the replication’s data extraction.
Besiroglu et al extracted data from a plot by first converting the pdf to Scalable Vector Graphic (SVG) format, and then processing the SVG file. A quick look at their python code suggested that the process was simpler than extracting directly from an uncompressed pdf file.
Accessing the data in the plot is only possible because the original image was created as a pdf, which contains information on the coordinates of all elements within the plot, not as a png or jpeg (which contain information about the colors appearing at each point in the image).
I experimented with this pdf-> svg -> csv route and quickly concluded that Besiroglu et al got lucky. The output from tools used to read-pdf/write-svg appears visually the same, however, internally the structure of the svg tags is different from the structure of the original pdf. I found that the original pdf was usually easier to process on a line by line basis. Besiroglu et al were lucky in that the svg they generated was easy to process. I suspect that the authors did not realize that pdf files need to be decompressed for the internal operations to be visible in an editor.
I decided to replicate the data extraction process using the original pdf as my source, not an extracted svg image. The original plots are below, and I extracted Model size/Training size for each of the points in the left plot (code+data):
What makes this replication and data interesting?
Chinchilla is a family of large language models, and this paper aimed to replicate an experimental study of the optimal model size and number of tokens for training a transformer language model within a specified compute budget. Given the many millions of £/$ being spent on training models, there is a lot of interest in being able to estimate the optimal training regimes.
The loss model fitted by Besiroglu et al, to the data they extracted, was a little different from the model fitted in the original paper:
Original: 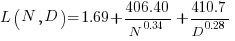
Replication: 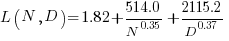
where:  is the number of model parameters, and
is the number of model parameters, and 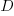 is the number of training tokens.
is the number of training tokens.
If data extracted from the pdf is different in some way, then the replication model will need to be refitted.
The internal pdf operations specify the x/y coordinates of each colored circle within a defined rectangle. For this plot, the bottom left/top right coordinates of the rectangle are: (83.85625, 72.565625), (421.1918175642, 340.96202) respectively, as specified in the first line of the extracted pdf operations below. The three values before each rg operation specify the RGB color used to fill the circle (for some reason duplicated by the plotting tool), and on the next line the /P0 Do is essentially a function call to operations specified elsewhere (it draws a circle), the six function parameters precede the call, with the last two being the x/y coordinates (e.g., x=154.0359138125, y=299.7658568695), and on subsequent calls the x/y values are relative to the current circle coordinates (e.g., x=-2.4321790463 y=-34.8834544196).
Q Q q 83.85625 72.565625 421.1918175642 340.96202 re W n 0.98137749 0.92061729 0.86536915 rg 0 G 0.98137749 0.92061729 0.86536915 rg 1 0 0 1 154.0359138125 299.7658568695 cm /P0 Do 0.97071849 0.82151775 0.71987163 rg 0.97071849 0.82151775 0.71987163 rg 1 0 0 1 -2.4321790463 -34.8834544196 cm /P0 Do |
The internal pdf x/y values need to be mapped to the values appearing on the visible plot’s x/y axis. The values listed along a plot axis are usually accompanied by tick marks, and the pdf operation to draw these tick marks will contain x/y values that can be used to map internal pdf coordinates to visible plot coordinates.
This plot does not have axis tick marks. However, vertical dashed lines appear at known Training FLOP values, so their internal x/y values can be used to map to the visible x-axis. On the y-axis, there is a dashed line at the 40B size point and the plot cuts off at the 100B size (I assumed this, since they both intersect the label text in the middle); a mapping to the visible y-axis just needs two known internal axis positions.
Extracting the internal x/y coordinates, mapping them to the visible axis values, and comparing them against the Besiroglu et al values, finds that the x-axis values agreed to within five decimal places (the conversion tool they used rounded the 10-digit decimal places present in the pdf), while the y-axis values appeared to differ differed by about 10%.
I initially assumed that the difference was due to a mistake by me; the internal pdf values were so obviously correct that there had to be a simple incorrect assumption I made at some point. Eventually, an internal consistency check on constants appearing in Besiroglu et al’s svg->csv code found the mistake. Besiroglu et al calculate the internal y coordinate of some of the labels on the y-axis by, I assume, taking the internal svg value for the bottom left position of the text and adding an amount they estimated to be half the character height. The python code is:
y_tick_svg_coords = [26.872, 66.113, 124.290, 221.707, 319.125] y_tick_data_coords = [100e9, 40e9, 10e9, 1e9, 100e6] |
The internal pdf values I calculated are consistent with the internal svg values 26.872, and 66.113, corresponding to visible y-axis values 100B and 40B. I could not find an accurate means of calculating character heights, and it turns out that Besiroglu et al’s calculation was not accurate.
I published the original version of this article, and contacted the first two authors of the paper (Besiroglu and Erdil). A few days later, Besiroglu replied with details of why they thought that the 40B line I was using as a reference point was actually at either 39.5B or 39.6B (based on published values for the Gopher budget on the x-axis), but there was uncertainty.
What other information was available to resolve the uncertainty? Ah, the right plot has Model size on the x-axis and includes lines that appear to correspond with axis values. The minimum/maximum Model size values extracted from the right plot closely match those in the original paper, i.e., that ’40B’ line is actually at 39.554B (mapping this difference from a log scale is enough to create the 10% difference in the results I calculated).
My thanks to Tamay Besiroglu and Ege Erdil for taking the time to explain their rationale.
The y-axis uses a log scale, and the ratio of the distance between the 10B/100B virtual tick marks and the 40B/100B virtual tick marks should be 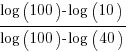 . The Besiroglu et al values are not consistent with this ratio; consistent values below (code+data):
. The Besiroglu et al values are not consistent with this ratio; consistent values below (code+data):
# y_tick_svg_coords = [26.872, 66.113, 124.290, 221.707, 319.125] y_tick_svg_coords = [26.872, 66.113, 125.4823, 224.0927, 322.703] |
When these new values are used in the python svg extraction code, the calculated y-axis values agree with my calculated y-axis values.
What is the equation fitted using these corrected Model size value? Answer below:
Replication: 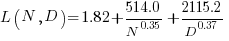
Corrected size: 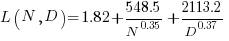
The replication paper also fitted the data using a bootstrap technique. The replication values (Table 1), and the corrected values are below (standard errors in brackets; code+data):
Parameter Replication Corrected
A 482.01 370.16
(124.58) (148.31)
B 2085.43 2398.85
(1293.23) (1151.75)
E 1.82 1.80
(0.03) (0.03)
α 0.35 0.33
(0.02) (0.02)
β 0.37 0.37
(0.02) (0.02) |
where the fitted equation is: 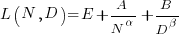
What next?
The data contains 245 rows, which is a small sample. As always, more data would be good.
Relative sizes of computer companies
How large are computer companies, compared to each other and to companies in other business areas?
Stock market valuation is a one measure of company size, another is a company’s total revenue (i.e., total amount of money brought in by a company’s operations). A company can have a huge revenue, but a low stock market valuation because it makes little profit (because it has to spend an almost equally huge amount to produce that income) and things are not expected to change.
The plot below shows the stock market valuation of IBM/Microsoft/Apple, over time, as a percentage of the valuation of tech companies on the US stock exchange (code+data on Github):
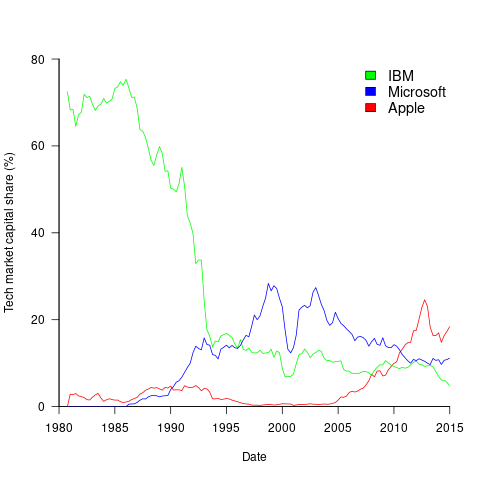
The growth of major tech companies, from the mid-1980s caused IBM’s dominant position to dramatically decline, while first Microsoft, and then Apple, grew to have more dominant market positions.
Is IBM’s decline in market valuation mirrored by a decline in its revenue?
The Fortune 500 was an annual list of the top 500 largest US companies, by total revenue (it’s now a global company list), and the lists from 1955 to 2012 are available via the Wayback Machine. Which of the 1,959 companies appearing in the top 500 lists should be classified as computer companies? Lacking a list of business classification codes for US companies, I asked Chat GPT-4 to classify these companies (responses, which include a summary of the business area). GPT-4 sometimes classified companies that were/are heavy users of computers, or suppliers of electronic components as a computer company. For instance, I consider Verizon Communications to be a communication company.
The plot below shows the ranking of those computer companies appearing within the top 100 of the Fortune 500, after removing companies not primarily in the computer business (code+data):
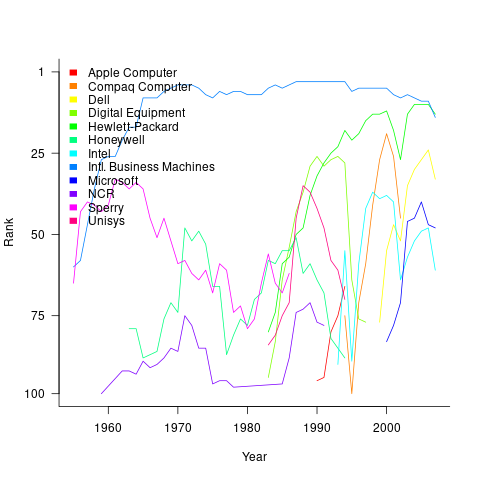
IBM is the uppermost blue line, ranking in the top-10 since the late-1960s. Microsoft and Apple are slowly working their way up from much lower ranks.
These contrasting plots illustrate the fact that while IBM continued to a large company by revenue, its low profitability (and major losses) and the perceived lack of a viable route to sustainable profitability resulted in it having a lower stock market valuation than computer companies with much lower revenues.
Average lines added/deleted by commits across languages
Are programs written in some programming language shorter/longer, on average, than when written in other languages?
There is a lot of variation in the length of the same program written in the same language, across different developers. Comparing program length across different languages requires a large sample of programs, each implemented in different languages, and by many different developers. This sounds like a fantasy sample, given the rarity of finding the same specification implemented multiple times in the same language.
There is a possible alternative approach to answering this question: Compare the size of commits, in lines of code, for many different programs across a variety of languages. The paper: A Study of Bug Resolution Characteristics in Popular Programming Languages by Zhang, Li, Hao, Wang, Tang, Zhang, and Harman studied 3,232,937 commits across 585 projects and 10 programming languages (between 56 and 60 projects per language, with between 58,533 and 474,497 commits per language).
The data on each commit includes: lines added, lines deleted, files changed, language, project, type of commit, lines of code in project (at some point in time). The paper investigate bug resolution characteristics, but does not include any data on number of people available to fix reported issues; I focused on all lines added/deleted.
Different projects (programs) will have different characteristics. For instance, a smaller program provides more scope for adding lots of new functionality, and a larger program contains more code that can be deleted. Some projects/developers commit every change (i.e., many small commit), while others only commit when the change is completed (i.e., larger commits). There may also be algorithmic characteristics that affect the quantity of code written, e.g., availability of libraries or need for detailed bit twiddling.
It is not possible to include project-id directly in the model, because each project is written in a different language, i.e., language can be predicted from project-id. However, program size can be included as a continuous variable (only one LOC value is available, which is not ideal).
The following R code fits a basic model (the number of lines added/deleted is count data and usually small, so a Poisson distribution is assumed; given the wide range of commit sizes, quantile regression may be a better approach):
alang_mod=glm(additions ~ language+log(LOC), data=lc, family="poisson") dlang_mod=glm(deletions ~ language+log(LOC), data=lc, family="poisson") |
Some of the commits involve tens of thousands of lines (see plot below). This sounds rather extreme. So two sets of models are fitted, one with the original data and the other only including commits with additions/deletions containing less than 10,000 lines.
These models fit the mean number of lines added/deleted over all projects written in a particular language, and the models are multiplicative. As expected, the variance explained by these two factors is small, at around 5%. The two models fitted are (code+data):
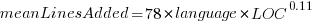 or
or 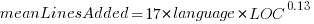 , and
, and 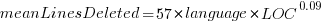 or
or 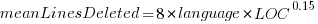 , where the value of
, where the value of 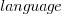 is listed in the following table, and
is listed in the following table, and 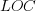 is the number of lines of code in the project:
is the number of lines of code in the project:
Original 0 < lines < 10000
Language Added Deleted Added Deleted
C 1.0 1.0 1.0 1.0
C# 1.7 1.6 1.5 1.5
C++ 1.9 2.1 1.3 1.4
Go 1.4 1.2 1.3 1.2
Java 0.9 1.0 1.5 1.5
Javascript 1.1 1.1 1.3 1.6
Objective-C 1.2 1.4 2.0 2.4
PHP 2.5 2.6 1.7 1.9
Python 0.7 0.7 0.8 0.8
Ruby 0.3 0.3 0.7 0.7 |
These fitted models suggest that commit addition/deletion both increase as project size increases, by around 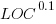 , and that, for instance, a commit in Go adds 1.4 times as many lines as C, and delete 1.2 as many lines (averaged over all commits). Comparing adds/deletes for the same language: on average, a Go commit adds
, and that, for instance, a commit in Go adds 1.4 times as many lines as C, and delete 1.2 as many lines (averaged over all commits). Comparing adds/deletes for the same language: on average, a Go commit adds 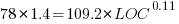 lines, and deletes
lines, and deletes 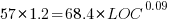 lines.
lines.
There is a strong connection between the number of lines added/deleted in each commit. The plot below shows the lines added/deleted by each commit, with the red line showing a fitted regression model 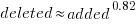 (code+data):
(code+data):
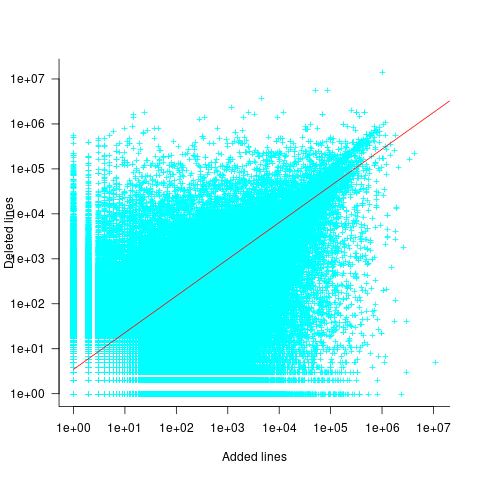
What other information can be included in a model? It is possible that project specific behavior(s) create a correlation between the size of commits; the algorithm used to fit this model assumes zero correlation. The glmer function, in the R package lme4, can take account of correlation between commits. The model component (language | project) in the following code adds project as a random effect on the language variable:
del_lmod=glmer(deletions ~ language+log(LOC)+(language | project), data=lc_loc, family=poisson) |
It takes around 24hr of cpu time to fit this model, which means I have not done much experimentation…

Recent Comments