Archive
CPU frequency not relevant to SPEC benchmark performance
Despite the end of Dennard scaling around 2005-7 computer performance, as measured by the SPEC cpu benchmarks, continues to improve. What is driving this ongoing increase in performance, given that cpu clock rates have stopped increasing?
The plot below shows 9,161 results from the SPEC CPU integer benchmark, plus the fitted regression line 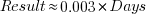 (code+data):
(code+data):
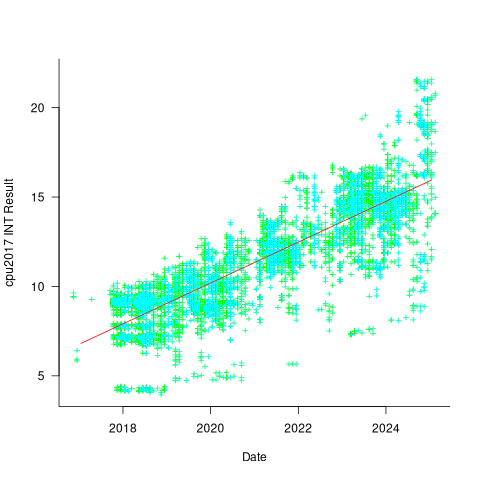
There is a scattering of benchmark results because manufacturers offer systems having a range of performance.
Possible factors driving the ongoing increases in system performance include increased DRAM-memory bandwidth, and cpu improvements such as larger caches and more accurate branch prediction. While Moore’s law (i.e., rate of growth of the number of transistors on a chip) has slowed down a lot, the number of transistors in a processor chip has continued to increase (many of these transistors have been used to build chips that contain multiple cpu cores).
The SPEC benchmark result data includes a lot of information about the system that ran the benchmarks, including: processor family/model, number of cpu cores, clock frequency, amount of memory installed and its type.
Results from SPEC CPU2017, the current version of the benchmark, are available from the start of 2017 to now. The following analysis uses these results. Results from the SPEC CPU2006 benchmark are also available, and a regression model fitted to the results from the 780 systems that ran both benchmarks, gives the mapping from CPU INT 2006 to CPU INT 2017 as: 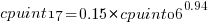 .
.
The processor information in the results file usually specifies family name plus model number/name. The model information usually correlates with clock frequency, perhaps cache size, or gpu support; some examples below.
AMD EPYC 4464P AMD EPYC 4564P
AMD Ryzen 9 7950X AMD Ryzen 7 5800X
Intel Xeon Platinum 8490H Intel Xeon Gold 6438N
Intel Xeon E3-1220 v3 Intel Xeon E5-2697 v3 |
The family name is sufficient for an initial analysis. Details of any cache size differences between models can always be included in a later analysis. The following table shows the number of processor x86 based families present in the 2017 INT results (total 9,161):
AMD EPYC AMD Ryzen Intel
1475 7 1
Intel Celeron Intel Core i3 Intel Core i5
16 31 2
Intel Core i7 Intel Pentium Intel Xeon
1 30 605
Intel Xeon Bronze Intel Xeon D Intel Xeon E3
167 12 16
Intel Xeon E5 Intel Xeon E7 Intel Xeon Gold
3 2 3994
Intel Xeon Platinum Intel Xeon Silver Intel Xeon W
1822 969 8 |
The memory information usually includes total bytes, number of memory sticks and interface standard (e.g., DDR2/3/4/5); some examples below.
64 GB (2 x 32 GB 2Rx4 PC5-5600B-R, running at 5200)
64 GB (2 x 32 GB 2Rx8 PC4-3200AA-E)
256 GB (8*1GB DDR2-400 DIMMS per 4 core module)
192 GB (4 x 12 x 4 GB DDR3-1333R, ECC, CL9)
32 GB (8 x 4 GB Dual-rank PC2-6400 CL5-5-5 FB-DIMMs)
24 GB (6 x 4 GB DDR3-1333 downclocked to 1066 MHz) |
The memory bandwidth can be calculated from the interface standard used. The names of modern DRAM interface standards start with either DDR or PC, and a number, a hyphen and then another number. The values appearing in the SPEC results don’t always follow the naming rules listed in the standard (e.g., last number of a PC name using the corresponding DDR number), and in a few cases a digit was dropped from the last number. Where possible the ‘obvious’ edits were made (sometimes values were just wrong), see code for details. The following table shows the number of interface standards represented in the 2017 CPU INT results (total 9,161; in the 2006 results DDR names predominated):
PC4-2400 PC4-2666 PC4-2933 PC4-3200 PC4-4800 PC5-11200 PC5-12800
26 2248 2163 2080 6 2 3
PC5-4800 PC5-5200 PC5-5600 PC5-6400 PC5-8 PC5-8800
1735 5 653 233 2 5 |
Once the memory is identified, its bandwidth can be looked up (bespoke memory stick clock rates were ignored). Fitting a regression model to the data, with the CPU INT (cpu integer benchmark) result as the outcome, we get (using a multiplicative model allows each factor to have a percentage impact; code+data):
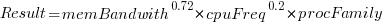
where: 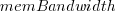 is the memory bandwidth in megabytes per second,
is the memory bandwidth in megabytes per second, 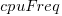 is cpu frequency in MHz, and
is cpu frequency in MHz, and 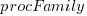 is the fitted constant for each processor family.
is the fitted constant for each processor family.
The cpu frequency varies between 1.7 and 4.7 GHz (a ratio of 1:2.8), the memory bandwidth between 19,200 and 51,200 MB/s (a ratio of 1:2.7), and processor family performance impact ratio was 1:2.2. Given the fitted power laws, this range of cpu frequencies could impact performance by around 22%, while the range of memory bandwidth could impact performance by a factor of two.
This fitted model implies that cpu frequency changes, over the range supported by systems since 2017, have almost no impact on the performance of integer-based programs, i.e., no floating point.
I thought there might be a correlation between memory bandwidth and cpu frequency (because vendors would use faster memory in systems with faster cpus). The plot below shows CPU frequency against memory bandwidth (both axis use linear scales), plus a fitted regression line in red (code+data):

I was wrong. There does not appear to be any connection between a system’s cpu frequency and its memory bandwidth.
These days, most x86 chips include multiple processors, with each processor taking a share of memory bandwidth. Increasing memory bandwidth is essential, if all cores are to be kept busy.
The SPEC CPU benchmark measures the performance of a single processor. If only one of the cpu cores available on a system is being used, that core has the benefit of memory bandwidth that usually has to be shared.
To what extent is a single core benchmark relevant today? I suspect that most programs run on a single core, but developers sometimes attempt to spread cpu intensive programs over multiple cores. As always, data is needed.
The SPEC benchmark is useful for cpu designers (the original target market) and compiler writers wanting to measure the impact of fancy new optimizations.
Memory bandwidth: 1991-2009
The Stream benchmark is a measure of sustained memory bandwidth; the target systems are high performance computers. Sustained in the sense of distance running, rather than a short sprint (the term for this is peak memory bandwidth and occurs when the requested data is in cache), and bandwidth in the sense of bytes of memory read/written per second (implemented using chunks the size of a double precision floating-point type). The dataset contains 1,018 measurements collected between 1991 and 2009.
The dominant characteristic of high performance computing applications is looping over very large arrays, performing floating-point operations on all the elements. A fast floating-point arithmetic unit has to be connected to a memory subsystem that can keep it fed with new floating-point values and write back computed values.
The Stream benchmark, in Fortran and C, defines several arrays, each containing max(1e6, 4*size_of_available_cache) double precision floating-point elements. There are four loops that iterate over every element of the arrays, each loop containing a single statement; see Fortran code in the following table (q is a scalar, array elements are usually 8-bytes, with add/multiply being the floating-point operations):
Name Operation Bytes FLOPS Copy a(i) = b(i) 16 0 Scale a(i) = q*b(i) 16 1 Sum a(i) = b(i) + c(i) 24 1 Triad a(i) = b(i) + q*c(i) 24 2 |
A system’s memory bandwidth will depend on the speed of the DRAM chips, the performance of the devices that transport bytes to the cpu, and the ability of the cpu to handle incoming traffic. The Stream data contains 21 columns, including: the vendor, date, clock rate, number of cpus, kind of memory (i.e., shared/distributed), and the bandwidth in megabytes/sec for each of the operations listed above.
How does the measured memory bandwidth change over time?
For most of the systems, the values for each of Copy, Scale, Sum, and Triad are very similar. That the simplest statement, Copy, is sometimes a bit faster/slower than the most complicated statement, Triad, shows that floating-point performance is much smaller than the time taken to read/write values to memory; the performance difference is random variation.
Several fitted regression models explain over half of the variance in the data, with the influential explanatory variables being: clock speed, date, type of system (i.e., PC/Mac or something much more expensive). The plot below shows MB/sec for the Copy loop, with three fitted regression models (code+data):
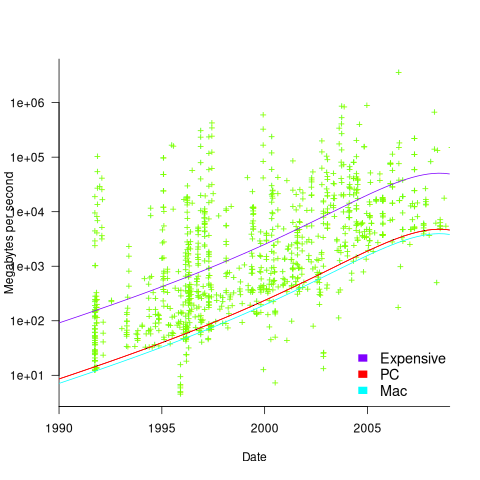
Fitting these models first required fitting a model for cpu clock rate over time; predictions of mean clock rate over time are needed as input to the memory bandwidth model. The three bandwidth models fitted are for PCs (189 systems), Macs (39 systems), and the more expensive systems (785; the five cluster systems were not fitted).
There was a 30% annual increase in memory bandwidth, with the average expensive systems having an order of magnitude greater bandwidth than PCs/Macs.
Clock rates stopped increasing around 2010, but go faster DRAM standards continue to be published. I assume that memory bandwidth continues to increase, but that memory performance is not something that gets written about much. The memory bandwidth on my new system is 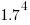 MB/sec. This 2024 sample of one is 3.5 times faster than the average 2009 PC bandwidth, which is 100 times faster than the 1991 bandwidth.
MB/sec. This 2024 sample of one is 3.5 times faster than the average 2009 PC bandwidth, which is 100 times faster than the 1991 bandwidth.
The LINPACK benchmarks are the traditional application oriented cpu benchmarks used within the high performance computer community.
Median system cpu clock frequency over last 15 years
We are all familiar with graphs showing the growth of cpu clock frequency over time. The data for these plots is based on vendor announcements listing the characteristics of their latest products, and invariably focuses on the product which is the fastest or contains the most transistors or the lowest power consumption.
Some customers buy the cpu with the highest/most/lowest, but many are happy to pay less for, for good enough. What does a graph of average customer cpu clock frequency over time look like?
Vendors sometimes publish general sales figures, but I have never seen one broken down by clock frequency. However, a few sites collect user system data, including:
- A subset of the Linux Counter project data is available. This does not contain explicit date information, but a must-be-later-than date can be inferred from the listed Linux kernel version,
- Hardware for BSD has data going back to December 2014, but there is no obvious way to extract it (I have not tried that hard),
- the BSDstats project (variable website availability) has been collecting data on machines running some derivative of BSD since August 2008; it contains around 200 times more cpu data than the known Linux Counter data. While the raw data is not available, approximately monthly reports are available on the Wayback Machine.
A BSDstats cpu history was obtained using waybackpack to download the available stored cpu summary pages, followed by html2text, and an awk script to extract the cpu frequency/count data.
BSDstats obtains the cpu information via a call to the sysctl command. For many Intel processors, but not AMD processors, the returned string includes the frequency (to see your cpu information on Linux systems type: more /proc/cpu), for instance:
Celeron(R) CPU 2.80GHz | 336 Pentium(R) 4 CPU 3.00GHz | 258 Pentium(R) 4 CPU 2.40GHz | 170 Athlon(tm) 64 Processor 3000+ | 43 Athlon(tm) 64 X2 Dual Core Processor 4200+ | 28 Athlon(tm) 64 Processor 3500+ | 27 |
For simplicity, only those rows containing frequency information were used in this analysis; 67% of the strings explicitly included a frequency (this saved me having to build a table to map AMD cpu strings to their corresponding frequency).
The plot below shows median cpu frequency (in red), along with the top/bottom 10% cpu frequencies, based on the Wayback Machine’s copy of the webpage on a given date, for a total of 2,304,446 cpu identities (code+data):
Broadly, the plot shows that cpu frequencies have essentially remained unchanged since 2008, with systems running BSD having a median frequency of 2.5 GHz, with 10% of systems having a frequency over 3.5 GHz, and 10% of systems a frequency below 1.5 GHz.
I was surprised at how many different frequencies were present in the data; often over 50. A look at the large number of different versions of Intel x86 cpus suggests that this is to be expected.
How representative is this sample of BSD systems, compared to the many more systems running Linux and Windows?
This begs the question of what kinds of environments are being compared. Are these desktop systems, local or hosted clusters, cloud systems?
The plot below shows the total number of cpus summarised on each Wayback Machine snapshot (code+data):

A few thousand systems are likely to be personal desktop systems, while the tens of thousands are likely to be clusters or small cloud providers.
Pointers to more data, particularly pre-2000, most welcome.
Relative performance of computers from the 1950s/60s/70s
What was the range of performance of computers introduced in the 1950, 1960s and 1970s, and what was the annual rate of increase?
People have been measuring computer performance since they were first created, and thanks to the Internet Archive the published results are sometimes available today. The catch is that performance was often measured using different benchmarks. Fortunately, a few benchmarks were run on many systems, and in a few cases different benchmarks were run on the same system.
I have found published data on four distinct system performance estimation models, with each applied to 100+ systems (a total of 1,306 systems, of which 1,111 are unique). There is around a 20% overlap between systems across pairs of models, i.e., multiple models applied to the same system. The plot below shows the reported performance for pairs of estimates for the same system (code+data):
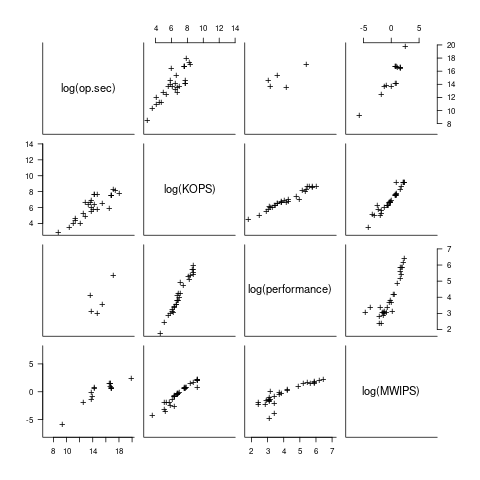
The relative performance relationship between pairs of different estimation models for the same system is linear (on a log scale).
Each of the models aims to produce a result that is representative of typical programs, i.e., be of use to people trying to decide which system to buy.
- Kenneth Knight built a structural model, based on 30 or so system characteristics, such as time to perform various arithmetic operations and I/O time; plugging in the values for a system produced a performance estimate. These characteristics were weighted based on measurements of scientific and commercial applications, to calculate a value that was representative of scientific or commercial operation. The Knight data appears in two magazine articles analysing systems from the 1950s and 1960s (the 310 rows are discussed in an earlier post), and the 1985 paper “A functional and structural measurement of technology”, containing data from the late 1960s and 1970s (120 rows),
- Ein-Dor and Feldmesser also built a structural model, based on the characteristics of 209 systems introduced between 1981 and 1984,
- The November 1980 Datamation article by Edward Lias lists what he called the KOPS (thousands of operations per second, i.e., MIPS for slower systems) value for 237 systems. Similar to the Knight and Ein-dor data, the calculated value is based on weighting various cpu instruction timings
- The Whetstone benchmark is based on running a particular program on a system, and recording its performance; this benchmark was designed to be representative of scientific and engineering applications, i.e., floating-point intensive. The design of this benchmark was the subject of last week’s post. I extracted 504 results from Roy Longbottom’s extensive collection of Whetstone results going back to the mid-1960s.
While the Whetstone benchmark was originally designed as an Algol 60 program that was representative of scientific applications written in Algol, only 5% of the results used this version of the benchmark; 85% of the results used the Fortran version. Fitting a regression model to the data finds that the Fortran version produced higher results than the Algol 60 version (which would encourage vendors to use the Fortran version). To ensure consistency of the Whetstone results, only those using the Fortran benchmark are used in this analysis.
A fifth dataset is the Dhrystone benchmark followed in the footsteps of the Whetstone benchmark, but targetting integer-based applications, i.e., no floating-point. First published in 1984, most of the Dhrystone results apply to more recent systems than the other benchmarks. This code+data contains the 328 results listed by the Performance Database Server.
Sometimes slightly different system names appear in the published results. I used the system names appearing in the Computers Models Database as the definitive names. It is possible that a few misspelled system names remain in the data (the possible impact is not matching systems up across models), please let me know if you spot any.
What is the best statistical technique to use to aggregate results from multiple models into a single relative performance value?
I came up with various possibilities, none of which looked that good, and even posted a question on Cross Validated (no replies yet).
Asking on the Evidence-based software engineering Discord channel produced a helpful reply from Neal Fultz, i.e., use the random effects model: lmer(log(metric) ~ (1|System)+(1|Bench), data=Sall_clean) ; after trying lots of other more complicated approaches, I would probably have eventually gotten around to using this approach.
Does this random effects model produce reliable values?
I don’t have a good idea how to evaluate the fitted model. Looking at pairs of systems where I know which is faster, the relative model values are consistent with what I know.
A csv of the calculated system relative performance values. I have yet to find a reliable way of estimating confidence bounds on these values.
The plot below shows the performance of systems introduced in a given year, on a relative scale, red line is a fitted exponential model (a factor of 5.5 faster, annually; code+data):
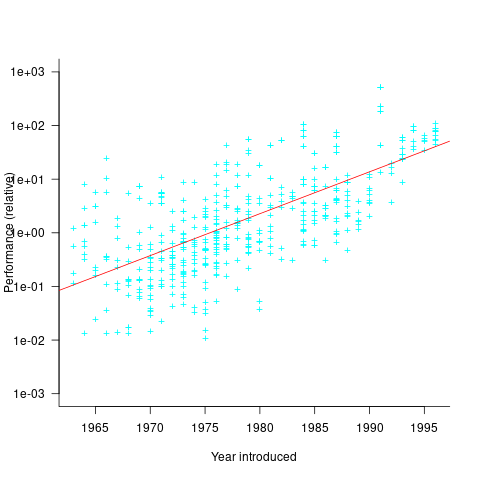
If you know of a more effective way of analysing this data, or any other published data on system benchmarks for these decades, please let me know.
The lifetime of performance coding issues
Coding activities that a developer might spend time on include: adding new functionality, fixing a reported fault, or fiddling with existing code with the intent of making it ‘better’ in some sense (which these days goes by the catch-all name of refactoring).
Improving performance, e.g., changing software to use less cpu/memory is considered, by developers, to make it ‘better’ (whether users are likely to notice the difference, or management see a ROI is for another article). There is a breed of developer whose DNA encodes for pleasure receptors that are only fire when working to reduce the amount of cpu/memory used by a program.
The paper Characterizing the evolution of statically-detectable performance issues of Android Apps by Das, Di Penta, and Malavolta studied the creation/removal of nine distinct performance coding issues in the source of 316 Android Apps (118 Apps contained five or more issues); a total of 2,408 performance issues were tracked.
What patterns might be present in the paper’s performance issues data?
I would expect there to be more creations in Apps containing more code, and more removals the longer an App is maintained; both very obvious. With more developers working on an App, there are going to be more creations and removals; do they cancel out? Management might decide to invest time in performance improvements for the next release, which would cause a spike in the number of removals per unit time.
How long do the nine performance issues survive in code, before being removed? The plot below shows the Kaplan Meier survival curve for Apps containing at least five issues (dotted blue/green are the 95% confidence intervals, code+data):
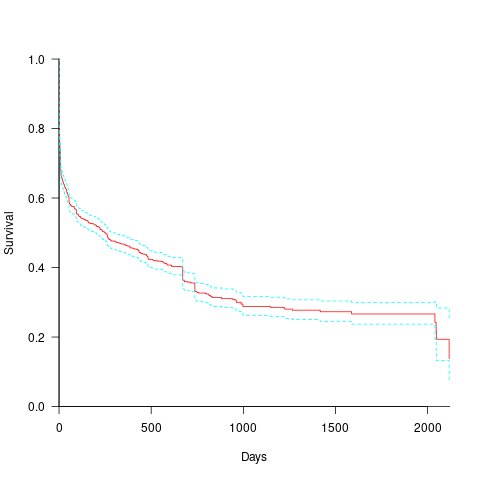
Around 15% of issues were removed on the day they are created, and by the eighth day around 30% had been removed. The roughly steady decline lasts for two-years, followed by almost stasis. Is two-years the active development lifetime of a successful Android App?
In isolation, the slope of the survival curve between eight days and two-years is not that interesting (it could be used to rule out models of the issue discovery process, e.g., happenstance discovery while working on other tasks). However, comparing it against the corresponding survival curve for reported faults tells us something about developer/management investment priorities for the two kinds of tasks, as measured by time to fix (which is a proxy for effort invested).
Unfortunately, this study did not collect information on coding mistake lifetimes, or time between a fault being reported and fixed. There have been studies investigating the survival time of coding mistakes. Reported faults should have the lowest survival rate, while the survival of coding mistakes will depend on the number of users (i.e., more users creates more opportunities to experience a fault and report it).
What factors influence performance issue time-to-fix?
The data includes information on the kind of performance issue, the number of times the App has been downloaded from the Google Play Store, and the number of contributors to the App.
Using these variables, a Cox proportional hazards model was fitted to model the survival time. In a proportional hazards model, the model coefficients are not absolute values, but provide ratio information. For instance, the following table shows the coefficients of the fitted model (code+data). Using these coefficients, we can compare the time taken to fix, say, a FloatMath issue relative to a ViewTag issue. The coefficient ratio 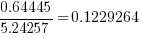 is the estimated ratio of fix times of the two respective issues.
is the estimated ratio of fix times of the two respective issues.
Coefficient Standard error Performance issue FloatMath 0.64445 0.14175 HandlerLeak 0.69958 0.12736 Recycle 0.83041 0.11386 UseSparseArrays 0.73471 0.12493 UseValueOf 0.64263 0.11827 ViewHolder 0.87253 0.14951 ViewTag 5.24257 0.46500 Wakelock 3.34665 0.72014 Downloads 50-100 0.62490 0.26245 100-500 0.64699 0.22494 500-1000 0.56768 0.23505 1000-5000 0.50707 0.22225 5000-10000 0.53432 0.22486 10000-50000 0.62449 0.21626 50000-100000 0.42214 0.23402 100000-500000 0.21479 0.25358 1000000-5000000 0.40593 0.21851 10000000-50000000 0.03474 0.61827 100000000-500000000 0.30693 0.39868 1000000000-5000000000 0.41522 0.61599 NA 0.03868 1.02076 Contributors 1.04996 0.01265 |
There is not a lot of difference in the coefficients for the number of downloads (the model fit is poor when the Standard error is close to the Coefficient value).
The paper Investigating Types and Survivability of Performance Bugs in Mobile Apps analyses a smaller dataset of performance issue lifetimes.
WebAssembly vs JavaScript performance: 2023 edition
WebAssembly is an assembly-like language intended to be executed by web browsers on an internal stack machine. The intent is that compilers for high-level languages (i.e., C, Cobol, and C#) treat WebAssembly just like they would the assembly language of a cpu. Some substantial applications have been ported, e.g., the R statistical environment, which is written in C and Fortran.
Some people claim that WebAssembly based applications will run faster, and consume less power, than those written in JavaScript or PHP. Now, one virtual machine is as much like any other. Performance differences are driven by compiler optimizations, the ease with which particular language features can be mapped to the available instructions, and an application’s use of easy/hard to map high-level language features.
Researchers have run benchmarks to compare the runtime performance and power consumption of Wasm against other browser based languages, and this post analyses the runtime performance results from two papers.
TL;DR: Relative performance for Wasm/JavaScript varies across browsers and programs. Everything interacts with everything else, which makes analysis complicated.
As is the case with most data analysis in software engineering, the researchers used rudimentary statistical techniques (which is a shame given the huge effort that went into collecting the data). The conclusions of both papers is that for WebAssembly/JavaScript, relative performance issues are complicated, but the techniques they used did not enable them to understand why.
What kind of statistical techniques are applicable for analysing these benchmarks?
Use of different languages/browsers might be expected to have some percentage impact on performance, e.g., programs written in language X will be p% faster/slower. The following equation is one modelling approach, and this equation can be fitted using nonlinear regression:
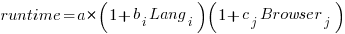 , where:
, where:  is a constant,
is a constant, 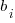 is the fitted constant for language
is the fitted constant for language 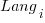 , and
, and 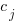 is the fitted constant for browser
is the fitted constant for browser 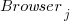
The problem with this equation is that it involves a separate equation for each combination of language/browser (assuming that all benchmarks are bundled together in the value of  ). It is possible to use a single equation when there are just two languages/two browsers, by mapping them to the values 0/1.
). It is possible to use a single equation when there are just two languages/two browsers, by mapping them to the values 0/1.
All languages/browsers/benchmarks can be included in a single linear regression model by treating them as factors in a log transformed model; the equation is: 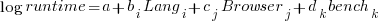 , where:
, where: 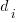 is the fitted constant for benchmark
is the fitted constant for benchmark 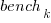 . The values of
. The values of 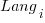 ,
, 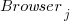 , and
, and 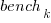 are zero, or one for the corresponding fitted constant. All the factors on the right-hand-side are discrete, so a log transform has nothing to distort.
are zero, or one for the corresponding fitted constant. All the factors on the right-hand-side are discrete, so a log transform has nothing to distort.
The fitted equation can then be transformed to:
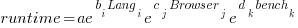
This model assumes that each factor is independent of the others, i.e., the relative performance of each language does not depend on the browser, and that relative performance does not significantly vary between benchmarks, e.g., if 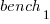 runs 10% faster when implemented in
runs 10% faster when implemented in 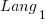 , then
, then 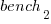 also runs close to 10% faster when implemented in
also runs close to 10% faster when implemented in 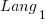 .
.
How well did the benchmark data from the two papers fit this model, and what were the performance numbers?
The study WebAssembly versus JavaScript: Energy and Runtime Performance by De Macedo, Abreu, Pereira, and Saraiva ran a wide range of benchmarks. It compared C/Wasm/JavaScript running on Chrome/Firefox/Edge. One set of benchmarks were 10 small compute-intensive programs (in Wasm/JavaScript), which were executed with small/medium/large amounts of input data; the other set of benchmarks were two large applications WasmBoy is a Game-boy/Gameboy Color Emulator (written in Typescript and compiled to Wasm), and PSPDFKit supporting viewing, annotating, and filling in forms in PDF documents (written in C/C++ and compiled to a both a subset of JavaScript and Wasm).
Results from the 10 small benchmarks showed strong interactions between browser and language (i.e., Wasm performance relative to JavaScript, varied between browsers; with Edge being faster and Firefox being slower), and a lot of interaction between benchmark and input data size. Support for Wasm is relatively new, relative to the much more mature JavaScript, so it’s not surprising that different browsers have different performance; I’m arm waving when I say that the input size dependency may be related to JIT issues (code).
When interactions are included, the fitted equation has the form:
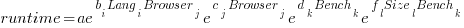
Analysing the results for the two applications, we find that:
- WasmBoy: the factors were independent, and WebAssembly was faster than JavaScript. The
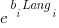 factor was 0.84 for Wasm and 1 for JavaScript,
factor was 0.84 for Wasm and 1 for JavaScript, - PSPDFKit: there was interaction between the language and browser, with behavior similar to that seen for the small benchmarks.
The study Comparing the Energy Efficiency of WebAssembly and JavaScript in Web Applications on Android Mobile Devices by van Hasselt, Huijzendveld, Noort, de Ruijter, Islam, and Malavolta compared the performance of WebAssembly/JavaScript running compute intensive benchmarks on Firefox/Chrome.
Fitting a regression model to the data from the eight benchmarks showed strong interactions between benchmark programs and language, with each language being faster for some programs (code).
It’s not surprising that the results failed to show a conclusive performance advantage for either WebAssembly or JavaScript, across benchmarks. The situation might change as the wasm virtual machine is tuned, and compilers targetting wasm implement a wider range of optimizations.
Update
A performance analysis of C, Rust, Go, and Javascript compiled to Webassembler
A comparison of C++ and Rust compiler performance
Large code bases take a long time to compile and build. How much impact does the choice of programming language have on compiler/build times?
The small number of industrial strength compilers available for the widely used languages makes the discussion as much about distinct implementations as distinct languages. And then there is the issue of different versions of the same compiler having different performance characteristics; for instance, the performance of Microsoft’s C++ Visual Studio compiler depends on the release of the compiler and the version of the standard specified.
Implementation details can have a significant impact on compile time. Compile time may be dominated by lexical analysis, while support for lots of fancy optimization shifts the time costs to code generation, and poorly chosen algorithms can result in symbol table lookup being a time sink (especially for large programs). For short programs, compile time may be dominated by start-up costs. These days, developers rarely have to worry about small memory size causing occurring when compiling a large source file.
A recent blog post compared the compile/build time performance of Rust and C++ on Linux and Apple’s OS X, and strager kindly made the data available.
The most obvious problem with attempting to compare the performance of compilers for different languages is that the amount of code contained in programs implementing the same functionality will differ (this is also true when the programs are written in the same language).
strager’s solution was to take a C++ program containing 9.3k LOC, plus 7.3K LOC of tests, and convert everything to Rust (9.5K LOC, plus 7.6K LOC of tests). In total, the benchmark consisted of compiling/building three C++ source files and three equivalent Rust source files.
The performance impact of number of lines of source code was measured by taking the largest file and copy-pasting it 8, 16, and 32 times, to create three every larger versions.
The OS X benchmarks did not include multiple file sizes, and are not included in the following analysis.
A variety of toolchain options were included in different runs, and for Rust various command line options; most distinct benchmarks were run 10 times each. On Linux, there were a total of 360 C++ runs, and for Rust 1,066 runs (code+data).
The model 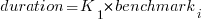 , where
, where 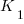 is a fitted regression constant, and
is a fitted regression constant, and 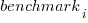 is the fitted regression coefficient for the
is the fitted regression coefficient for the 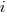 ‘th benchmark, explains just over 50% of the variance. The language is implicit in the benchmark information.
‘th benchmark, explains just over 50% of the variance. The language is implicit in the benchmark information.
The model 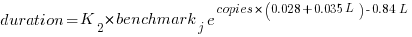 , where
, where 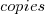 is the number of copies,
is the number of copies, 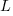 is 0 for C++ and 1 for Rust, explains 92% of the variance, i.e., it is a very good fit.
is 0 for C++ and 1 for Rust, explains 92% of the variance, i.e., it is a very good fit.
The expression 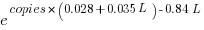 is a language and source code size multiplication factor. The numeric values are:
is a language and source code size multiplication factor. The numeric values are:
1 8 16 32 C++ 1.03 1.25 1.57 2.45 Rust 0.98 1.52 2.52 6.90 |
showing that while Rust compilation is faster than C++, for ‘shorter’ files, it becomes much relatively slower as the quantity of source increases.
The size factor for Rust is growing quadratically, while it is much closer to linear for C++.
What are the threats to the validity of this benchmark comparison?
The most obvious is the small number of files benchmarked. I don’t have any ideas for creating a larger sample.
How representative is the benchmark of typical projects? An explicit goal in benchmark selection was to minimise external dependencies (to reduce the effort likely to be needed to translate to Rust). Typically, projects contain many dependencies, with compilers sometimes spending more time processing dependency information than compiling the actual top-level source, e.g., header files in C++.
A less obvious threat is the fact that the benchmarks for each language were run in contiguous time intervals, i.e., all Rust, then all C++, then all Rust (see plot below; code+data):

It is possible that one or more background processes were running while one set of language benchmarks was being run, which would skew the results. One solution is to intermix the runs for each language (switching off all background tasks is much harder).
I was surprised by how well the regression model fitted the data; the fit is rarely this good. Perhaps a larger set of benchmarks would increase the variance.
Moore’s law was a socially constructed project
Moore’s law was a socially constructed project that depended on the coordinated actions of many independent companies and groups of individuals to last for as long it did.
All products evolve, but what was it about Moore’s law that enabled microelectronics to evolve so much faster and for longer than most other products?
Moore’s observation, made in 1965 based on four data points, was that the number of components contained in a fabricated silicon device doubles every year. The paper didn’t make this claim in words, but a line fitted to four yearly data points (starting in 1962) suggested this behavior continuing into the mid-1970s. The introduction of IBM’s Personal Computer, in 1981 containing Intel’s 8088 processor, led to interested parties coming together to create a hugely profitable ecosystem that depended on the continuance of Moore’s law.
The plot below shows Moore’s four points (red) and fitted regression model (green line). In practice, since 1970, fitting a regression model (purple line) to the number of transistors in various microprocessors (blue/green, data from Wikipedia), finds that the number of transistors doubled every two years (code+data):
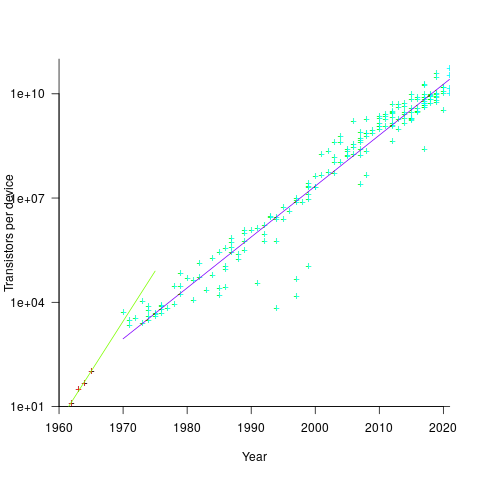
In the early days, designing a device was mostly a manual operation; that is, the circuit design and logic design down to the transistor level were hand-drawn. This meant that creating a device containing twice as many transistors required twice as many engineers. At some point the doubling process either becomes uneconomic or it takes forever to get anything done because of the coordination effort.
The problem of needing an exponentially-growing number of engineers was solved by creating electronic design automation tools (EDA), starting in the 1980s, with successive generations of tools handling ever higher levels of abstraction, and human designers focusing on the upper levels.
The use of EDA provides a benefit to manufacturers (who can design differentiated products) and to customers (e.g., products containing more functionality).
If EDA had not solved the problem of exponential growth in engineers, Moore’s law would have maxed-out in the early 1980s, with around 150K transistors per device. However, this would not have stopped the ongoing shrinking of transistors; two economic factors independently incentivize the creation of ever smaller transistors.
When wafer fabrication technology improvements make it possible to double the number of transistors on a silicon wafer, then around twice as many devices can be produced (assuming unchanged number of transistors per device, and other technical details). The wafer fabrication cost is greater (second row in table below), but a lot less than twice as much, so the manufacturing cost per device is much lower (third row in table).
The doubling of transistors primarily provides a manufacturer benefit.
The following table gives estimates for various chip foundry economic factors, in dollars (taken from the report: AI Chips: What They Are and Why They Matter). Node, expressed in nanometers, used to directly correspond to the length of a particular feature created during the fabrication process; these days it does not correspond to the size of any specific feature and is essentially just a name applied to a particular generation of chips.
Node (nm) 90 65 40 28 20 16/12 10 7 5 Foundry sale price per wafer 1,650 1,937 2,274 2,891 3,677 3,984 5,992 9,346 16,988 Foundry sale price per chip 2,433 1,428 713 453 399 331 274 233 238 Mass production year 2004 2006 2009 2011 2014 2015 2017 2018 2020 Quarter Q4 Q4 Q1 Q4 Q3 Q3 Q2 Q3 Q1 Capital investment per wafer 4,649 5,456 6,404 8,144 10,356 11,220 13,169 14,267 16,746 processed per year Capital consumed per wafer 411 483 567 721 917 993 1,494 2,330 4,235 processed in 2020 Other costs and markup 1,293 1,454 1,707 2,171 2,760 2,990 4,498 7,016 12,753 per wafer |
The second economic factor incentivizing the creation of smaller transistors is Dennard scaling, a rarely heard technical term named after the first author of a 1974 paper showing that transistor power consumption scaled with area (for very small transistors). Halving the area occupied by a transistor, halves the power consumed, at the same frequency.
The maximum clock-frequency of a microprocessor is limited by the amount of heat it can dissipate; the heat produced is proportional to the power consumed, which is approximately proportional to the clock-frequency. Instead of a device having smaller transistors consume less power, they could consume the same power at double the frequency.
Dennard scaling primarily provides a customer benefit.
Figuring out how to further shrink the size of transistors requires an investment in research, followed by designing/(building or purchasing) new equipment. Why would a company, who had invested in researching and building their current manufacturing capability, be willing to invest in making it obsolete?
The fear of losing market share is a commercial imperative experienced by all leading companies. In the microprocessor market, the first company to halve the size of a transistor would be able to produce twice as many microprocessors (at a lower cost) running twice as fast as the existing products. They could (and did) charge more for the latest, faster product, even though it cost them less than the previous version to manufacture.
Building cheaper, faster products is a means to an end; that end is receiving a decent return on the investment made. How large is the market for new microprocessors and how large an investment is required to build the next generation of products?
Rock’s law says that the cost of a chip fabrication plant doubles every four years (the per wafer price in the table above is increasing at a slower rate). Gambling hundreds of millions of dollars, later billions of dollars, on a next generation fabrication plant has always been a high risk/high reward investment.
The sales of microprocessors are dependent on the sale of computers that contain them, and people buy computers to enable them to use software. Microprocessor manufacturers thus have to both convince computer manufacturers to use their chip (without breaking antitrust laws) and convince software companies to create products that run on a particular processor.
The introduction of the IBM PC kick-started the personal computer market, with Wintel (the partnership between Microsoft and Intel) dominating software developer and end-user mindshare of the PC compatible market (in no small part due to the billions these two companies spent on advertising).
An effective technique for increasing the volume of microprocessors sold is to shorten the usable lifetime of the computer potential customers currently own. Customers buy computers to run software, and when new versions of software can only effectively be used in a computer containing more memory or on a new microprocessor which supports functionality not supported by earlier processors, then a new computer is needed. By obsoleting older products soon after newer products become available, companies are able to evolve an existing customer base to one where the new product is looked upon as the norm. Customers are force marched into the future.
The plot below shows sales volume, in gigabytes, of various sized DRAM chips over time. The simple story of exponential growth in sales volume (plus signs) hides the more complicated story of the rise and fall of succeeding generations of memory chips (code+data):
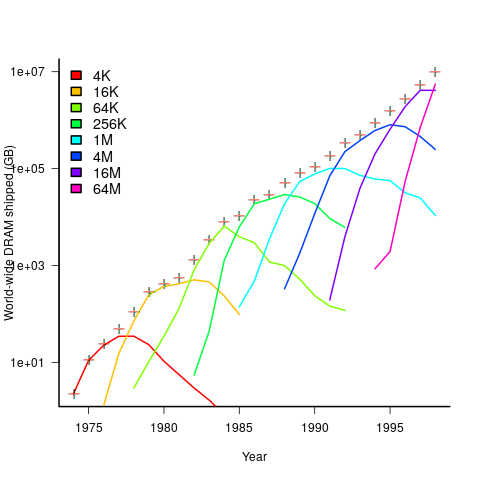
The Red Queens had a simple task, keep buying the latest products. The activities of the companies supplying the specialist equipment needed to build a chip fabrication plant has to be coordinated, a role filled by the International Technology Roadmap for Semiconductors (ITRS). The annual ITRS reports contain detailed specifications of the expected performance of the subsystems involved in the fabrication process.
Moore’s law is now dead, in that transistor doubling now takes longer than two years. Would transistor doubling time have taken longer than two years, or slowed down earlier, if:
- the ecosystem had not been dominated by two symbiotic companies, or did network effects make it inevitable that there would be two symbiotic companies,
- the Internet had happened at a different time,
- if software applications had quickly reached a good enough state,
- if cloud computing had gone mainstream much earlier.
Where are the industrial strength R compilers?
Why don’t compiler projects for the R language make it into production use? The few that have been written have remained individual experimental products, e.g., RLLVMCompile.
Most popular languages attract many compiler implementations. I’m not saying that any of these implementations have more than a handful of users, that they implement the full language (a full implementation is not common), or that they fulfil any need other than their implementers desire to build something.
A commonly heard reason for the lack of production R compilers is that it is not worth the time and effort, because most of an R program’s time is spent in the library code which is written in a compiled language (e.g., C or Fortran). The fact that it is probably not worth the time and effort has not stopped people writing compilers for other languages, but then I think that the kind of people who use R tend not to be the kind of people who want to spend their time writing compilers. On the whole, they are the kind of people who are into statistics and data analysis.
Is it true that that most R programs spend most of their time executing library code? It’s certainly true for me. But I have noticed that a lot of the library functions executed by my code are written in R. Also, if somebody uses R for all their programming needs (it might be the only language they know), then their code might not be heavily library dependent.
I was surprised to read about Tierney’s byte code compiler, because his implementation is how I thought the R-core’s existing implementation worked (it does now). The internals of R is based on 1980s textbook functional techniques, and like many book implementations of the day, performance is dependent on the escape hatch of compiled code. R’s implementers wisely spent their time addressing user concerns, which revolved around statistics and visual presentation, i.e., not internal implementation technicalities.
Building an R compiler is easy, the much harder and time-consuming part is the runtime system.
Threaded code is a quick and simple approach to compiler implementation. R source gets mapped to a sequence of C function calls, with these functions proving a wrapper to library functions implementing the appropriate basic functionality, e.g., add two vectors. This approach has been the subject of at least one Master’s thesis. Thesis implementations rarely reach production use because those involved significantly underestimate the work that remains to be done, which is usually a lot more than the original implementation.
A simple threaded code approach provides a base for subsequent optimization, with the base having a similar performance to an interpreter. Optimizing requires figuring out details of the operations performed and replacing generic function calls with ones designed to be fast for specific cases, or even better replacing calls with inline code, e.g., adding short vectors of integers. There is a lot of existing work for scripting languages and a few PhD thesis researching R (e.g., Wang). The key technique is static analysis of R source.
Jan Vitek is running what appears to be the most active R compiler research group, at the moment e.g., the Ř project. Research can be good for uncovering language usage and trying out different techniques, but it is not intended to produce industry strength code. Lots of the fancy optimizations in early versions of the gcc C compiler started life as a PhD thesis, with the respective individual sometimes going on to spend a few years creating a production quality version for the released compiler.
The essential ingredient for building a production compiler is persistence. There are an awful lot of details that need to be sorted out (this is why research project code does not directly translate to production code, they ignore ‘minor’ details in order to concentrate on the ‘interesting’ research problem). Is there a small group of people currently beavering away on a production quality compiler for R? If there is, I can understand being discrete, on long-term projects it can be very annoying to have people regularly asking when the software is going to be released.
To have a life, once released, a production compiler needs to attract users, who are often loyal to their current compiler (because they know that their code works for this compiler); there needs to be a substantial benefit to entice people to switch. The benefit of compiling R to machine code, rather than interpreting, is performance. What performance improvement is needed to attract a viable community of users (there is always a tiny subset of users who will pay lots for even small performance improvements)?
My R code is rarely cpu bound, so I am not in the target audience, no matter what the speed-up. I don’t have any insight in the performance problems experienced by the R community, and have no idea whether a factor of two, five, ten or more would be enough.
Scientific management of software production
When Frederick Taylor investigated the performance of workers in various industries, at the start of the 1900’s, he found that workers organise their work to suit themselves; workers were capable of producing significantly more than they routinely produced. This was hardly news. What made Taylor’s work different was that having discovered the huge difference between actual worker output and what he calculated could be achieved in practice, he was able to change work practices to achieve close to what he had calculated to be possible. Changing work practices took several years, and the workers did everything they could to resist it (Taylor’s The principles of scientific management is an honest and revealing account of his struggles).
Significantly increasing worker output pushed company profits through the roof, and managers everywhere wanted a piece of the action; scientific management took off. Note: scientific management is not a science of work, it is a science of the management of other people’s work.
The scientific management approach has been successfully applied to production where most of the work can be reduced to purely manual activities (i.e., requiring little thinking by those who performed them). The essence of the approach is to break down tasks into the smallest number of component parts, to simplify these components so they can be performed by less skilled workers, and to rearrange tasks in a way that gives management control over the production process. Deskilling tasks increases the size of the pool of potential workers, decreasing labor costs and increasing the interchangeability of workers.
Given the almost universal use of this management technique, it is to be expected that managers will attempt to apply it to the production of software. The software factory was tried, but did not take-off. The use of chief programmer teams had its origins in the scarcity of skilled staff; the idea is that somebody who knows what they were doing divides up the work into chunks that can be implemented by less skilled staff. This approach is essentially the early stages of scientific management, but it did not gain traction (see “Programmers and Managers: The Routinization of Computer Programming in the United States” by Kraft).
The production of software is different in that once the first copy has been created, the cost of reproduction is virtually zero. The human effort invested in creating software systems is primarily cognitive. The division between management and workers is along the lines of what they think about, not between thinking and physical effort.
Software systems can be broken down into simpler components (assuming all the requirements are known), but can the implementation of these components be simplified such that they can be implemented by less skilled developers? The process of simplification is practical when designing a system for repetitive reproduction (e.g., making the same widget again and again), but the first implementation of anything is unlikely to be simple (and only one implementation is needed for software).
If it is not possible to break down the implementation such that most of the work is easy to do, can we at least hire the most productive developers?
How productive are different developers? Programmer productivity has been a hot topic since people started writing software, but almost no effective research has been done.
I have no idea how to measure programmer productivity, but I do have some ideas about how to measure their performance (a high performance programmer can have zero productivity by writing programs, faster than anybody else, that don’t do anything useful, from the client’s perspective).
When the same task is repeatedly performed by different people it is possible to obtain some measure of average/minimum/maximum individual performance.
Task performance improves with practice, and an individual’s initial task performance will depend on their prior experience. Measuring performance based on a single implementation of a task provides some indication of minimum performance. To obtain information on an individual’s maximum performance they need to be measured over multiple performances of the same task (and of course working in a team affects performance).
Should high performance programmers be paid more than low performance programmers (ignoring the issue of productivity)? I am in favour of doing this.
What about productivity payments, e.g., piece work?
This question is a minefield of issues. Manual workers have been repeatedly found to set informal quotas amongst themselves, i.e., setting a maximum on the amount they will produce during a shift (see “Money and Motivation: An Analysis of Incentives in Industry” by William Whyte). Thankfully, I don’t think I will be in a position to have to address this issue anytime soon (i.e., I don’t see a reliable measure of programmer productivity being discovered in the foreseeable future).
Recent Comments