Archive
Sampling error in software engineering
In the physical sciences, measurement error occurs because of accuracy limits on the device used to make the measurement and the interpretation of the data by the person doing the measurement.
In software engineering, some measurements appear to be error free. For instance, lines of code is a discrete value that is easily counted. While some people don’t include blank lines and/or comments, the choice of what to count does not prevent an exact count being made.
In physics, the behavior of particular elements does not depend on the identity of which atoms are measured, while in software the behavior of programs written to the same specification can have different characteristics, e.g., lines of code.
For instance, each implementation of the 3n+1 problem will contain some number of LOC, with other implementations often containing a different number of LOC. The plot below shows the distribution of LOC for 6,301 implementations of 3n+1 (code and data):
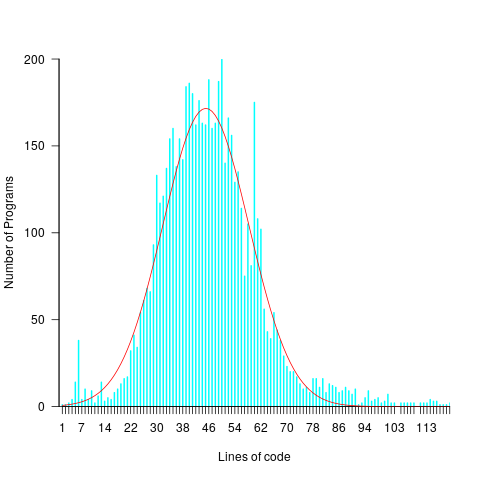
Each program implementing the 3n+1 problem is one sample from the population of programs implementing the 3n+1 specification. Different people are likely to implement different programs, and the same person may create different implementations at different times.
Sampling error occurs when the characteristics of a sample are used to infer characteristics about the population from which the sample was drawn.
How might sampling error affect the results of data analysis?
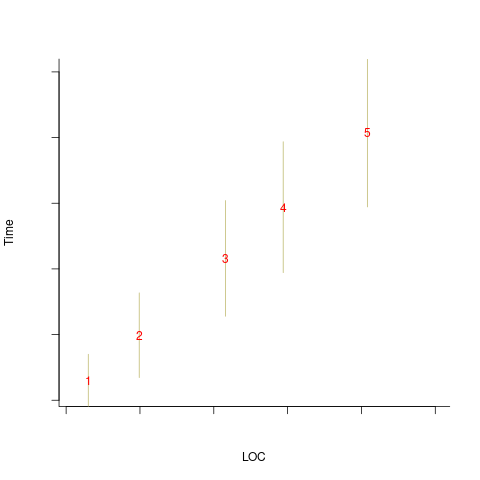
An example, using made-up values: Assume that two sets of sample measurements are made of the time taken to implement five different specifications, along with the lines of code contained in the implementations (in the same language). In the plot below, the yellow circles show a range of likely implementation measurements for each of the five specifications. The green dots, one for each specification, are measurements of one sample of programs implementing each specification; the blue dots are a second sample of programs (code):
The green and blue lines show the ordinary least squares regression model fitted to each sample. The different samples selected from the five populations has produced what appears to be slightly different models. How significant is this difference in the fitted models?
The grey line denotes where LOC is proportional to implementation time, which is one hypothesis of software project progress. The green line sample implies that LOC growth decreases as implementation time increases, while the blue line sample implies the reverse (both have been proposed as hypotheses of software project progress).
The difference in this example is important because the models fitted to the samples straddle the demarcation line between alternative theories of software project development.
A larger sample may not produce a more accurate model; a previous post analyses such a case. The example above shows a symmetric uniformly distributed population because that is the easiest to plot. In practice, populations distributions are likely to be asymmetric and irregular, e.g., measured time may be rounded to the nearest appropriate unit.
The mathematics underpinning OLS assumes that there is no error in the explanatory variables (LOC in the above plot), and that all the error is concentrated in the response variable (Time in the above plot). When there is a non-trivial sample error, or measurement error, OLS is not the appropriate technique to use to fit a regression model. The plot below shows the sample error that is assumed by OLS (code):
When there is a non-trivial error in the explanatory variable (LOC in this example), the appropriate technique for fitting a regression model is errors-in-variables regression.
Building an errors-in-variables regression model requires values for the error in the variables appearing in the equation to be fitted. Obtaining these values can be very difficult (Deming regression is a fitting technique based on the ratio of the errors).
In the above example, what is the likely variability in the implementation time and LOC, for a given specification? The limited data on the LOC contained in multiple implementations of the same specification suggests that the standard deviation of the LOC across implementations of the same specification is around 25% of the mean.
Learning researchers have run experiments where each subject performs the same task multiple times. Performance improves with practice, which makes it difficult to calculate the likely variability in the first-time performance.
My book: Evidence-based software engineering recommends using SIMEX to fit errors-in-variables models (section 11.2.3). This technique takes a model fitted using existing methods (allowing a wide range of models to be fitted), and then refits the model created based on the estimated error in one or more explanatory variables (no need to estimate an error in the response variable, the technique makes use of the value from the initial fit).
A surprising retrospective task estimation dataset
When estimating the time needed to implement a task, the time previously needed to implement similar tasks provides useful guidance. The implementation time for these previous tasks may itself be estimated, because the actual time was not measured or this information is currently unavailable.
How accurate are developer time estimates of previously completed tasks?
I am not aware of any software related dataset of estimates of previously completed tasks (it’s hard enough finding datasets containing information on the actual implementation time). However, I recently found the paper Dynamics of retrospective timing: A big data approach by Balcı, Ünübol, Grondin, Sayar, van Wassenhove, and Wittmann. The data analysed comes from a survey questionnaire, where 24,494 people estimated the how much time they had spent answering the questions, along with recording the current time at the start/end of the questionnaire. The supplementary data is in MATLAB format, and is also available as a csv file in the Blursday database (i.e., RT_Datasets).
Some of the behavior patterns seen in software engineering estimates appear to be general human characteristics, e.g., use of round numbers. An analysis of the estimation performance of a wide sample of the general population could help separate out characteristics that are specific to software engineering and those that apply to the general population.
The following table shows the percentage of answers giving a particular Estimate and Actual time, in minutes. Over 60% of the estimates are round numbers. Actual times are likely to be round numbers because people often give a round number when asked the time (code+data):
Minutes Estimate Actual
20 18% 8.5%
15 15% 5.3%
30 12% 7.6%
25 10% 6.2%
10 7.7% 2.1% |
I was surprised to see that the authors had fitted a regression model with the Actual time as the explanatory variable and the Estimate as the response variable. The estimation models I have fitted always have the roles of these two variables reversed. More of this role reversal difference below.
The equation fitted to the data by the authors is (they use the term Elapsed, for consistency with other blog articles I continue to use Actual; code+data):
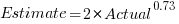
This equation says that, on average, for shorter Actual times the Estimate is higher than the Actual, while for longer Actual times the average Estimate is lower.
Switching the roles of the variables, I expected to see a fitted model whose coefficients are somewhat similar to the algebraically transformed version of this equation, i.e.,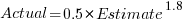 
. At the very least, I expected the exponent to be greater than one.
Surprisingly, the equation fitted with the variables roles reversed is very similar, i.e., the equations are the opposite of each other:
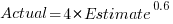
This equation says that, on average, for shorter Estimate times the Actual time is higher than the Estimate, while for longer Estimate times the average Actual is lower, i.e., the opposite behavior specifie dby the earlier equation.
I spent some time trying to understand how it was possible for data to be fitted such that (x ~ y) == (y ~ x), even posting a question to Cross Validated. I might, in a future post, discuss the statistical issues behind this behavior.
So why did the authors of this paper treat Actual as an explanatory variable?
After a flurry of emails with the lead author, Fuat Balcı (who was very responsive to my questions), where we both doubled checked the code/data and what we thought was going on, Fuat answered that (quoted with permission):
“The objective duration is the elapsed time (noted by the experimenter based on a clock reading), and the estimate is the participant’s response. According to the psychophysical approach the mapping between objective and subjective time can be defined by regressing the subjective estimates of the participants on the objective duration noted by the experimenter. Thus, if your research question is how human’s retrospective experience of time changes with the duration of events (e.g., biases in time judgments), the y-axis should be the participant’s response and the x-axis should be the actual duration.”
This approach has a logic to it, and is consistent with the regression modelling done by other researchers who study retrospective time estimation.
So which modelling approach is correct, and are people overestimating or underestimating shorter actual time durations?
Going back to basics, the structure of this experiment does not produce data that meets one of the requirements of the statistical technique we are both using (ordinary least squares) to fit a regression model. To understand why ordinary least squares, OLS, is not applicable to this data, it’s necessary to delve into a technical detail about the mathematics of what OLS does.
The equation actually fitted by OLS is: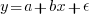 
, where 
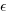is an error term (i.e., ‘noise’ caused by all the effects other than 
). The value of is assumed to be exact, i.e., not contain any ‘noise’.
Usually, in a retrospective time estimation experiment, subjects hear, for instance, a sound whose duration is decided in advance by the experimenter; subjects estimate how long each sound lasted. In this experimental format, it makes sense for the Actual time to appear on the right-hand-side as an explanatory variable and for the Estimate response variable on the left-hand-side.
However, for the questionnaire timing data, both the Estimate and Actual time are decided by the person giving the answers. There is no experimenter controlling one of the values. Both the Estimate and Actual values contain ‘noise’. For instance, on a different day a person may have taken more/less time to actually answer the questionnaire, or provided a different estimate of the time taken.
The correct regression fitting technique to use is errors-in-variables. An errors-in-variables regression fits the equation: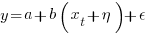 
, where: 
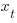is the true value of and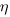 
is its associated error. A selection of packages are available for fitting a variety of errors-in-variables models.
I regularly see OLS used in software engineering papers (including mine) where errors-in-variables is the technically correct technique to use. Researchers are either unaware of the error issues or assuming that the difference is not important. The few times I have fitted an errors-in-variables model, the fitted coefficients have not been much different from those fitted by an OLS model; for this dataset the coefficient difference is obviously important.
The complication with building an errors-in-variables model is that values need to be specified for the error terms 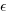and 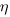. With OLS the value of 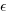is produced as part of the fitting process.
How might the required error values be calculated?
If some subjects round reported start/stop times, there may not be any variation in reported Actual time, or it may jump around in 5-minute increments depending on the position of the minute hand on the clock.
Learning researchers have run experiments where each subject performs the same task multiple times. Performance improves with practice, which makes it difficult to calculate the likely variability in the first-time performance. If we assume that performance is skill based, the standard deviation of all the subjects completing within a given timeframe could be used to calculate an error term.
With 60% of Estimates being round numbers, there might not be any variation for many people, or perhaps the answer given will change to a different round number. There is Estimate data for different, future tasks, and a small amount of data for the same future tasks. There is data from many retrospective studies using very short time intervals (e.g., tens of seconds), which might be applicable.
We could simply assume that the same amount of error is present in each variable. Deming regression is an errors-in-variables technique that supports this approach, and does not require any error values to be specified. The following equations have been fitted using Deming regression (code+data):
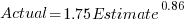
and
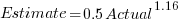
While these two equations are consistent with each other, we don’t know if the assumption of equal errors in both variables is realistic.
What next?
Hopefully it will be possible to work out reasonable error values for the Actual/Estimate times. Fitting a model using these values will tell us wether any over/underestimating is occurring, and the associated span of time durations.
I also need to revisit the analysis of software task estimation times.
Workshop on data analysis for software developers
I’m teaching a workshop on data analysis for software engineers on 22 June. The workshop is organized by the British Computer Society’s SPA specialist group, and can be attended remotely.
Why is there a small registration charge (between £2 and £15)? Typically, 30% to 50% of those registered for a free event actually turn up. It is very frustrating when all the places are taken, people are turned away, and then only half those registered turn up. We decided to charge a minimal amount to deter the uncommitted, and include lunch. Why the variable pricing? The BCS have a rule that members have to get a discount, and HMRC does not allow paid+free options (I suspect this has more to do with the software the BCS are using).
It’s a hands-on workshop that aims to get people up and running with practical data analysis. As always, my data analysis hammer of choice is regression analysis.
A few things are being updated since I last gave this workshop?
While my completed book Evidence-based Software Engineering was not available when the last workshop was given, the second half containing the introductory statistics material was available for download. There has not been any major changes to the statistical material in this second half.
The one new statistical observation I plan to highlight is that in software engineering, there is a lot of data that does not have a normal distribution. Many data analysis are aimed at the social sciences (the biggest market), and they frequently just assume that all the data is normally distributed; software engineering data is different.
For a very long time I have known that most developers/managers do not collect and analyse measurements of their development processes. However, I had underestimated ‘most’, which I now think is at least 99%.
Given the motivation, developers/managers would measure and analyse processes. I plan to update the material to have a motivational theme, along with illustrating the statistical points being made. The purpose of the motivational examples is to give attendees something to take back and show their managers/coworkers: Look, we can find out where all our money/time is being wasted. I assume that attendees are already interested in analysing software engineering data (why else would they be spending a Saturday at the workshop).
I have come up with a great way of showing how many of software engineering’s cited ‘facts’ are simply folklore derived from repeating opinions from papers published long ago (or derived from pitifully small amounts of data). The workshop is hands-on, with attendees individually working through examples. The plan is for examples to be based on the data behind some of these ‘facts’, e.g., Halstead & McCabe metrics, and COCOMO.
Tips, and suggestions for topics to discuss welcome.
Survey papers: LLMs will restore some level of usefulness
Scientific papers are like soap operas, in that understanding them requires readers to have some degree of familiarity with the ongoing plot.
How can people new to an opera quickly get up to speed with the ongoing story lines, without reading hundreds of papers?
The survey paper is intended to be the answer to this question. Traditionally written by an established researcher in the field, the 100+ pages aim to be an authoritative overview of the progress and setbacks of research on a particular topic within the last 5/10/15 years (depending on the rate/lack of progress since the last major survey paper).
These days research papers are often written by PhD students, with the professor doing the supervising, and getting their name tacked on to the end of the list of authors (professors can spend more time writing grant applications than writing research papers). Writing a single 100+ page survey paper is not a cost-effective use of an experienced person’s time, given the pressure to pump out papers, even when the ACM Computing Surveys is one of the highest ranked journals in computing. The short lifecycle of fields driven by the next fashionable topic is another disincentive.
Given the incentives, why are survey papers still being published?
In software engineering there are now two kinds of survey papers: 1) the traditional kind, written by people who see it as a service, or are not on the publish/perish treadmill, or early stage researchers surveying a niche topic, 2) PhD students using what we now call a Large language model summary approach, soon to be replaced by real LLMs.
So-called survey papers (at least in software engineering) are now regularly being written by members of the intended audience of traditional survey papers, i.e., PhD students who are new to the field and want a map of the territory showing the routes to the frontiers.
How does a person who knows almost nothing about a field write a (20-40 page, rarely 100+) survey paper about it?
A survey is based on the list of all the appropriate papers. In theory, appropriate papers have to meet some quality criteria, e.g., be published in a reputable journal/conference/blog. In practice, the list is created by searching various academic publication search engines (e.g., web of science, or the ACM digital library) using a targeted regular expression; for instance:
(agile OR waterfall OR software OR "story points" OR "story point" OR "user stories" OR "function points" OR "planning poker" OR "pomodoros" OR "use case" OR "source code" OR "DORA metrics" OR scrum) (predict OR prediction OR quantify OR dataset OR schedule OR lifecycle OR "life cycle" OR estimate OR estimates OR estimating OR estimation OR estimated OR #noestimates OR "evidence" OR empirical OR evolution OR ecosystems OR cognitive OR economics OR reliability OR metrics OR experiment) |
The list of papers returned may be filtered further, depending on how many there are (a hundred or two does not look too lightweight, and does not require an excessive amount of work).
Next, what to say about these papers, and how many of them actually need to be read?
The bottom of the barrel, vacant ideas, survey paper tabulates easily calculated metrics (e.g., number of papers per year, number of authors per paper, clusters of keywords), and babble on about paper selection criteria, keyword growth and diversity, and more research is needed.
For a survey paper to appear in a layer above the vacant ideas level, the authors have to process some amount of the paper contents. The paper A Systematic Literature Review on Reasons and Approaches for Accurate Effort Estimations in Agile by Pasuksmit, Thongtanunam, and Karunasekera is a recent example of one such survey. The search criteria returned 519 papers, of which 82 were selected for inclusion, i.e., cited. The first 10, of the 42 pages, covered the selection process and the process used to answer the two research questions; RQ1: What are the discovered reasons for inaccurate estimations in Agile iterative development? and RQ2: What are the approaches proposed to improve effort estimation in Agile iterative development?
The main answers to the research questions appeared in: 1) tables which listed attributes relating to the question and the papers that had something to say about that attribute, and 2) sections containing a few paragraphs highlighting various points made by papers about some attribute.
My primary interest was Table 11, which listed the papers/dataset used. A few were new to me, but unfortunately all confidential.
A survey can only be as good as the papers it is based on. The regular expression approach can miss important papers and include unimportant papers. The Pasuksmit et al paper only included one paper by the leading researcher in Agile effort estimation, and included papers that I wouldn’t waste disk space on a pdf file.
I would not recommend these ‘LLM’ style surveys to newcomers to a field. They don’t connect the lines of research, call out the successes/failures, and they don’t provide a map of the territory.
The readership of these survey papers are the experienced researchers, who will scan the list of cited papers looking for anything they might have missed.
I’m not expecting LLMs to be capable of producing experienced professor level survey papers any time soon. In a year or two, LLMs will surely be doing a better job than PhD students.
Recent Comments