Archive
Optimal sizing of a product backlog
Developers working on the implementation of a software system will have a list of work that needs to be done, a to-do list, known as the product backlog in Agile.
The Agile development process differs from the Waterfall process in that the list of work items is intentionally incomplete when coding starts (discovery of new work items is an integral part of the Agile process). In a Waterfall process, it is intended that all work items are known before coding starts (as work progresses, new items are invariably discovered).
Complaints are sometimes expressed about the size of a team’s backlog, measured in number of items waiting to be implemented. Are these complaints just grumblings about the amount of work outstanding, or is there an economic cost that increases with the size of the backlog?
If the number of items in the backlog is too low, developers may be left twiddling their expensive thumbs because they have run out of work items to implement.
A parallel is sometimes drawn between items waiting to be implemented in a product backlog and hardware items in a manufacturer’s store waiting to be checked-out for the production line. Hardware occupies space on a shelf, a cost in that the manufacturer has to pay for the building to hold it; another cost is the interest on the money spent to purchase the items sitting in the store.
For over 100 years, people have been analyzing the problem of the optimum number of stock items to order, and at what stock level to place an order. The economic order quantity gives the optimum number of items to reorder, 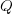 (the derivation assumes that the average quantity in stock is
(the derivation assumes that the average quantity in stock is 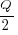 ), it is given by:
), it is given by:
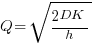 , where
, where  is the quantity consumed per year,
is the quantity consumed per year,  is the fixed cost per order (e.g., cost of ordering, shipping and handling; not the actual cost of the goods),
is the fixed cost per order (e.g., cost of ordering, shipping and handling; not the actual cost of the goods), 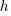 is the annual holding cost per item.
is the annual holding cost per item.
What is the likely range of these values for software?
 is around 1,000 per year for a team of ten’ish people working on multiple (related) projects; based on one dataset,
is around 1,000 per year for a team of ten’ish people working on multiple (related) projects; based on one dataset, is the cost associated with the time taken to gather the requirements, i.e., the items to add to the backlog. If we assume that the time taken to gather an item is less than the time taken to implement it (the estimated time taken to implement varies from hours to days), then the average should be less than an hour or two,
is the cost associated with the time taken to gather the requirements, i.e., the items to add to the backlog. If we assume that the time taken to gather an item is less than the time taken to implement it (the estimated time taken to implement varies from hours to days), then the average should be less than an hour or two,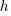 : While the cost of a post-it note on a board, or an entry in an online issue tracking system, is effectively zero, there is the time cost of deciding which backlog items should be implemented next, or added to the next Sprint.
: While the cost of a post-it note on a board, or an entry in an online issue tracking system, is effectively zero, there is the time cost of deciding which backlog items should be implemented next, or added to the next Sprint.
If the backlog starts with
 items, and it takes
items, and it takes  seconds to decide whether a given item should be implemented next, and
seconds to decide whether a given item should be implemented next, and  is the fraction of items scanned before one is selected: the average decision time per item is:
is the fraction of items scanned before one is selected: the average decision time per item is: 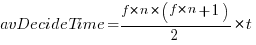 seconds. For example, if
seconds. For example, if 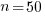 , pulling some numbers out of the air,
, pulling some numbers out of the air, 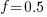 , and
, and 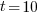 , then
, then 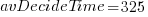 , or 5.4 minutes.
, or 5.4 minutes.The Scrum approach of selecting a subset of backlog items to completely implement in a Sprint has a much lower overhead than the one-at-a-time approach.
If we assume that 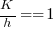 , then
, then 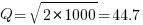 .
.
An ‘order’ for 45 work items might make sense when dealing with clients who have formal processes in place and are not able to be as proactive as an Agile developer might like, e.g., meetings have to be scheduled in advance, with minutes circulated for agreement.
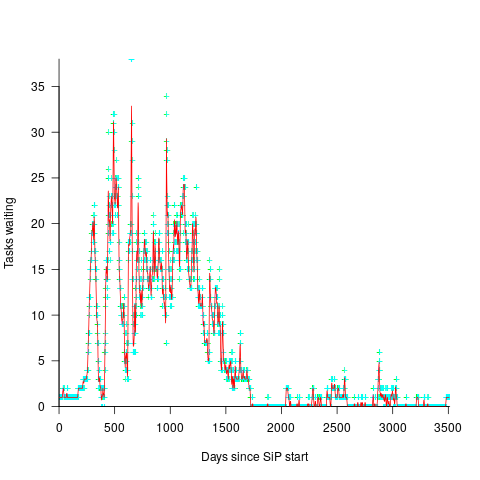
In a more informal environment, with close client contacts, work items are more likely to trickle in or appear in small batches. The SiP dataset came from such an environment. The plot below shows the number of tasks in the backlog of the SiP dataset, for each day (blue/green) and seven-day rolling average (red) (code+data):
Over/under estimation factor for ‘most estimates’
When asked to estimate the time taken to perform a software development related task, people regularly over or under estimate. What range of over/under estimation falls within the bounds of the term ‘most estimates’, i.e., the upper/lower bounds of the ratio 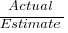 (an overestimate occurs when
(an overestimate occurs when 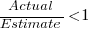 , an underestimate when
, an underestimate when 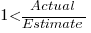 )?
)?
On Twitter, I have been citing a factor of two for over/under time estimates. This factor of two involves some assumptions and a personal interpretation.
The following analysis is based on the two major software task effort estimation datasets: SiP and CESAW. The tasks in both datasets are for internal projects (i.e., no tendering against competitors), and require at most a few hours work.
The following analysis is based on the SiP data.
Of the 8,252 unique tasks in the SiP data, 30% are underestimates, 37% exact, and 33% overestimates.
How do we go about calculating bounds for the over/under factor of most estimates (a previous post discussed calculating an accuracy metric over all estimates)?
A simplistic approach is to average over each of the overestimated and underestimated tasks. The plot below shows hours estimated against the ratio actual/estimated, for each task (code+data):
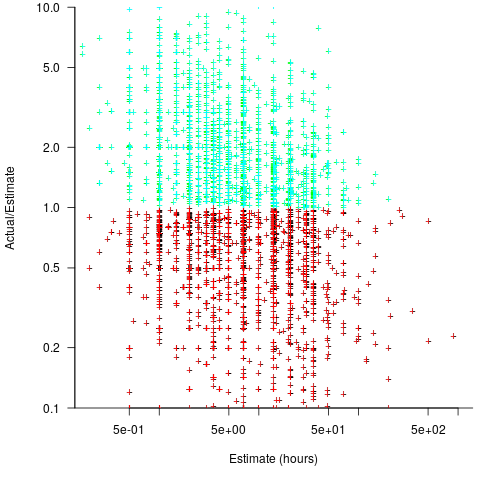
Averaging the over/under estimated tasks separately (using the geometric mean) gives 0.47 and 1.9 respectively, i.e., tasks are over/under estimated by a factor of two.
This approach fails to take into account the number of estimates that are over/under/equal, i.e., it ignores likelihood information.
A regression model takes into account the distribution of values, and we could adopt the fitted model’s prediction interval as the over/under confidence intervals. The prediction interval is the interval within which other observations are expected to fall, with some probability (R’s predict function uses one standard deviation).
The plot below shows a fitted regression model and prediction intervals at one standard deviation (68.3%) and two standard deviations (95%); the faint grey line shows Estimate == Actual (code+data):
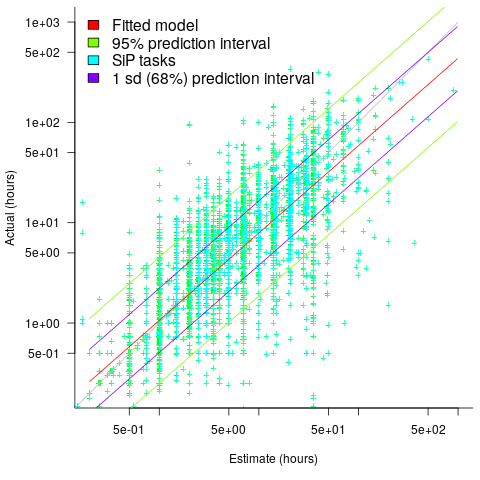
The fitted model tilts down from the upward direction of the Estimate == Actual line, consequently the over/under estimation factor depends on the size of the estimate. The table below lists the over/under estimation factor for low/high estimates at one & two standard deviations (68.3 and 95% probability).
People like simple answers (i.e., single values) and the mean value is a commonly used technique of summarising many values. The task estimate values are unevenly distributed and weighting the mean by the distribution of estimated values is more representative than, say, an evenly distributed set of estimates. The 5th and 6th columns in the table below list the weighted means at one/two standard deviations (the CESAW columns are the values for all projects in the CESAW data).
1 sd 2 sd Weighted mean CESAW
Low High Low High 1 sd 2 sd 1 sd 2 sd
Over 0.56 0.24 0.27 0.11 0.46 0.25 0.29 0.1
Under 2.4 1.0 4.9 2.0 2.00 4.1 2.4 6.5 |
The weighted means for over/under estimates are close to a factor of two of the actual (divide/multiply) within one standard deviation (68.3%), and a factor of four within two standard deviations (95%).
Why choose to give the one standard deviation factor, rather than the two? People talk of “most estimates”, but what percentage range does ‘most’ map to? I have tended to think of ‘most’ as more than two-thirds, e.g., at least one standard deviation (a recent study suggests that ‘most’ usage peaks at 80-85%), and I think of two standard deviations as ‘nearly all’ (i.e., 95%; there are probably people who call this ‘most’).
Perhaps a between two and four is a more appropriate answer (particularly since the bounds are wider for the CESAW data). Suggestions welcome.
Including natural language text topics in a regression model
The implementation records for a project sometimes include a brief description of each task implemented. There will be some degree of similarity between the implementation of some tasks. Is it possible to calculate the degree of similarity between tasks from the text in the task descriptions?
Over the years, various approaches to measuring document similarity have been proposed (more than you probably want to know about natural language processing).
One of the oldest, simplest and widely used technique is term frequency–inverse document frequency (tf-idf), which is based on counting word frequencies, i.e., is word context is ignored. This technique can work well when there are a sufficient number of words to ensure a good enough overlap between similar documents.
When the description consists of a sentence or two (i.e., a summary), the problem becomes one of sentence similarity, not document similarity (so tf-idf is unlikely to be of any use).
Word context, in a sentence, underpins the word embedding approach, which represents a word by an n-dimensional vector calculated from the local sentence context in which the word occurs (derived from a large amount of text). Words that are closer, in this vector space, are expected to have similar meanings. One technique for calculating the similarity between sentences is to compare the averages of the word embedding of the words they contain. However, care is needed; words appearing in the same context can create sentences having different meanings, as in the following (calculated sentence similarity in the comments):
import spacy nlp=spacy.load("en_core_web_md") # _md model needed for word vectors nlp("the screen is black").similarity(nlp("the screen is white")) # 0.9768339369182919 # closer to 1 the more similar the sentences nlp("implementing widgets would be little effort").similarity(nlp("implementing widgets would be a huge effort")) # 0.9636533803238744 nlp("the screen is black").similarity(nlp("implementing widgets would be a huge effort")) # 0.6596892830922606 |
The first pair of sentences are similar in that they are about the characteristics of an object (i.e., its colour), while the second pair are similar in that are about the quantity of something (i.e., implementation effort), and the third pair are not that similar.
The words in a document, or summary, are about some collection of topics. A set of related documents are likely to contain a discussion of a set of related topics in varying degrees. Latent Dirichlet allocation (LDA) is a widely used technique for calculating a set of (unseen) topics from a set of documents and their contained words.
A recent paper attempted to estimate task effort based on the similarity of the task descriptions (using tf-idf). My last semi-serious attempt to extract useful information from text, some years ago, was a miserable failure (it’s a very hard problem). Perhaps better techniques and tools are now available for me to leverage (my interest is in understanding what is going on, not making predictions).
My initial idea was to extract topics from task data, and then try to add these to regression models of task effort estimation, to see what impact they had. Searching to find out what researchers have recently been doing in this area, I was pleased to see that others were ahead of me, and had implemented R packages to do the heavy lifting, in particular:
- The
stmpackage supports the creation of Structural Topic Models; these add support for covariates to influence the process of fitting LDA models, i.e., a correlation between the topics and other variables in the data. Uses of STM appear to be oriented towards teasing out differences in topics associated with different values of some variable (e.g., political party), and the package authors have written papers analysing political data. - The
psychtmpackage supports what the authors call supervised latent Dirichlet allocation with covariates (SLDAX). This handles all the details needed to include the extracted LDA topics in a regression model; exactly what I was after. The user interface and documentation for this package is not as polished as thestmpackage, but the code held together as I fumbled my way through.
To experiment using these two packages I used the SiP dataset, which includes summary text for each task, and I have previously analysed the estimation task data.
The stm package:
The textProcessor function handles all the details of converting a vector of strings (e.g., summary text) to internal form (i.e., handling conversion to lower case, removing stop words, stemming, etc).
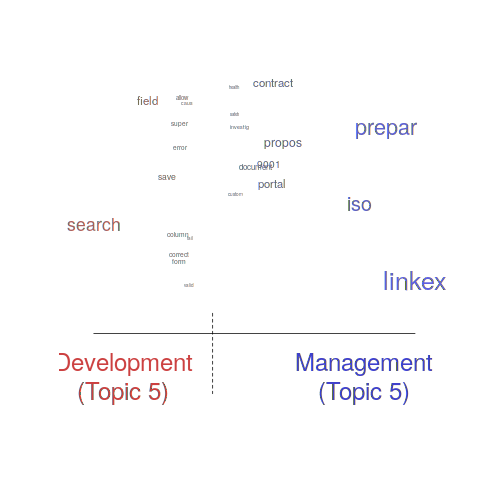
One of the input variables to the LDA process is the number of topics to use. Picking this value is something of a black art, and various functions are available for calculating and displaying concepts such as topic semantic coherence and exclusivity, the most commonly used words associated with a topic, and the documents in which these topics occur. Deciding the extent to which 10 or 15 topics produced the best results (values that sounded like a good idea to me) required domain knowledge that I did not have. The plot below shows the extent to which the words in topic 5 were associated with the Category column having the value “Development” or “Management” (code+data):
The psychtm package:
The prep_docs function is not as polished as the equivalent stm function, but the package’s first release was just last year.
After the data has been prepared, the call to fit a regression model that includes the LDA extracted topics is straightforward:
sip_topic_mod=gibbs_sldax(log(HoursActual) ~ log(HoursEstimate), data = cl_info,
docs = docs_vocab$documents, model = "sldax",
K = 10 # number of topics) |
where: log(HoursActual) ~ log(HoursEstimate) is the simplest model fitted in the original analysis.
The fitted model had the form: 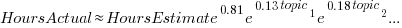 , with the calculated coefficient for some topics not being significant. The value
, with the calculated coefficient for some topics not being significant. The value 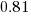 is close to that fitted in the original model. The value of
is close to that fitted in the original model. The value of 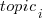 is the fraction of the
is the fraction of the 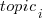 calculated to be present in the Summary text of the corresponding task.
calculated to be present in the Summary text of the corresponding task.
I’m please to see that a regression model can be improved by adding topics derived from the Summary text.
The SiP data includes other information such as work Category (e.g., development, management), ProjectCode and DeveloperId. It is to be expected that these factors will have some impact on the words appearing in a task Summary, and hence the topics (the stm analysis showed this effect for Category).
When the model formula is changed to: log(HoursActual) ~ log(HoursEstimate)+ProjectCode, the quality of fit for most topics became very poor. Is this because ProjectCode and topics conveyed very similar information, or did I need to be more sophisticated when extracting topic models? This needs further investigation.
Can topic models be used to build prediction models?
Summary text can only be used to make predictions if it is available before the event being predicted, e.g., available before a task is completed and the actual effort is known. My interest in model building is to understand the processes involved, so I am not worried about when the text was created.
My own habit is to update, or even create Summary text once a task is complete. I asked Stephen Cullen, my co-author on the original analysis and author of many of the Summary texts, about the process of creating the SiP Summary sentences. His reply was that the Summary field was an active document that was updated over time. I suspect the same is true for many task descriptions.
Not all estimation data includes as much information as the SiP dataset. If Summary text is one of the few pieces of information available, it may be possible to use it as a proxy for missing columns.
Perhaps it is possible to extract information from the SiP Summary text that is not also contained in the other recorded information. Having been successful this far, I will continue to investigate.
Wanted: 99 effort estimation datasets
Every now and again, I stumble upon a really interesting dataset. Previously, when this happened I wrote an extensive blog post; but the SiP dataset was just too big and too detailed, it called out for a more expansive treatment.
How big is the SiP effort estimation dataset? It contains 10,100 unique task estimates, from ten years of commercial development using Agile. That’s around two orders of magnitude larger than other, current, public effort datasets.
How detailed is the SiP effort estimation dataset? It contains the (anonymized) identity of the 22 developers making the estimates, for one of 20 project codes, dates, plus various associated items. Other effort estimation datasets usually just contain values for estimated effort and actual effort.
Data analysis is a conversation between the person doing the analysis and the person(s) with knowledge of the application domain from which the data came. The aim is to discover information that is of practical use to the people working in the application domain.
I suggested to Stephen Cullum (the person I got talking to at a workshop, a director of Software in Partnership Ltd, and supplier of data) that we write a paper having the form of a conversation about the data; he bravely agreed.
The result is now available: A conversation around the analysis of the SiP effort estimation dataset.
What next?
I’m looking forward to seeing what other people do with the SiP dataset. There are surely other patterns waiting to be discovered, and what about building a simulation model based on the charcteristics of this data?
Turning software engineering into an evidence-based disciple requires a lot more data; I plan to go looking for more large datasets.
Software engineering researchers are a remarkable unambitious bunch of people. The SiP dataset should be viewed as the first of 100 such datasets. With 100 datasets we can start to draw general, believable conclusions about the processes involved in software effort estimation.
Readers, today is the day you start asking managers to make any software engineering data they have publicly available. Yes, it can be anonymized (I am willing to do that for people who are looking to release data). Yes, ‘old’ data is useful (data from the 1980s could have an interesting story to tell; SiP runs from 2004-2014). Yes, I will analyze any interesting data that is made public for free.
Ask, and you shall receive.
Recent Comments