Archive
Creating a global Standard requires being politically neutral
Governments actively promote Standards because following them saves their citizens time and money. The UK and US have contrasting rationales, with the UK focusing on savings achieved through repeated use of standardized items and the US focusing on the repeated use of skills people acquired through using a standardized item (i.e., reduced training costs).
Manufacturers wanting to export products want to be able to ship identical products all over the world, i.e., not have to make costly changes for different national markets. To be able to do this, they need the rest of the world to have a Standard way of doing things. The once dominant military and industrial status of Great Britain, and now the US, motivated them to create and encourage other countries to follow the Standards they created.
These days, most programming language Standards work is done by people employed by US companies attending an international committee, SC22, with (currently) 28 countries paying to be P (participating) members and 21 countries as O (observing) members (most countries don’t appear to have any active involvement in language standards). The reason for the dominance of US companies is that few non-US companies are willing to fund staff to do Standard’s work. For a few languages SC22 essentially rubber stamps documents produced elsewhere, e.g., most of the Cobol work used to be done by a US committee and ECMAScript (aka JavaScript) work is done in a European committee mostly attended by US companies.
Other countries sometimes get to dominate the creation of a language Standard, e.g., the UK led the Pascal Standard work. At the last SC22 meeting, a person from the US lamented that Europe was set to become the dominant driver of the Ada Standard. I resisted the urge to cheer: Make Europe Great Again.
Getting an international Standard adopted throughout the world requires that ISO be politically neutral and accept any sovereign country as a member (provided they pay the membership fees). For instance, North Korea is a member of ISO.
The only politics I have previously seen in programming language standard meetings has involved company rivalry, not geopolitical rivalry. A recent request for comment from SC2 (the ISO committee responsible for coded character sets; readers are more likely to be familiar with Unicode, essentially the same information published by a non-profit consortium based in California) looks like geopolitics, in the sense of geopolitical virtue signalling.
The document is: Request for SC2 member comments on proposal to encode “Ruble sign with double vertical stem”. What does the character “Ruble sign with double vertical stem” look like? To quote the document: “The proposed character is a text element that cannot be represented by any existing character or character sequence.” Readers will have to imagine Russia’s Ruble currency symbol, ₽, with two vertical stems (I assume these stems are short antennae like lines).
What is the geopolitical connection? Readers will be aware of Russia’s invasion of Ukraine, but may not be aware of Russia’s involvement in Transnistria (quoting Wikipedia, “… a landlocked breakaway state internationally recognized as part of Moldova.”). Since 1994, the proposed character has been used as the Transnistria currency symbol.
The request for comment includes a “Non-technical considerations” section summarises various controversy points, and finishes with: “We are not aware of any non-technical criteria having been used by SC2 or WG2 in the past that could be applied to disqualify this character. We are also concerned that adopting a criterion that allows for opposing a character because of association with politically or socially defined user communities could be problematic.”
The proposed character is not included in ISO 4217 (which defines numeric codes for the representation of currencies). However, SC22 does not require that a character used to represent a currency be included in ISO 4217. Previously, SC22 has accepted currency characters that are not in ISO 4217.
Is this a one-off objection, or does it mark the start of a stream of requests to remove one or more politically incorrect characters from ISO 10646/Unicode?
A lot of people put a lot of effort into creating a unified Standard for all the characters created by the World’s people. I hope the destructive nature of virtue signalling does not take hold in programming language Standard ecosystem.
Student projects for 2024/2025
It will soon be that time of year when university students are looking for an interesting idea for a project. On an irregular basis, I post some ideas for thesis projects (here and here); primarily for students studying computing. In a change of direction, this post suggests software related ideas for business student projects.
Two idea areas require data analysis skills, one requires people skills, and one an interest in theory.
More suggestions welcome in the comments.
Career paths in software
Organizations employ people to work on software systems. What is the career path of people who work on software systems? Question include: how long people stay in a particular job or company, and salary changes over time (the only data I know of investigates the career paths of 500 people working in IT).
Governments are interested in employment, and they collect and publish data at various levels of granularity. The US Bureau of Labor Statistics contains a vast amount of information, but finding the bits of interest can require a lot of work.
In the US, government employee salary is public information, and various sites make this available, e.g., OpePayrolls and Transparent California. There is a Japanese Open Salaries, and various commercial companies operate an open salary policy (Buffer is perhaps the most famous).
This project requires students with some data analysis skills.
There is some data on job postings,
Computer company lifecycle
Companies are born, do business and eventually die (unless bought/merged). How do the lifecycle characteristics of computer companies differ from companies doing business in other domains? Lifecycle characteristics of interest might include profiles of age, number of employees, and profitability. What are the consequences, if any, of these differences?
Details of all UK registered companies are freely available from Companies House.
Open Corporates provides company information from across the world, but it is not free in bulk.
Some analysis of the geographical clustering of software companies in the UK.
This project requires students with some data analysis skills.
AI startup ecosystem
AI has exploded on the tech scene, and lots of people are creating startups to build services/products around LLMs. Teams are very fluid, with people moving around a lot looking for a viable service/product. Sometimes these teams form companies, and these might eventually leave stealth mode and become visible. What are the characteristics of the AI startup ecosystem within a city; questions include: how many people are working within it, their backgrounds, and the business areas are they focusing on?
This project requires students with people skills and a willingness to get out and about. Much of the current AI ecosystem is only visible to those within it. Evening meetups and workshops offer a way into this personal network. This research involves bootstrapping the data gathering by spending evenings schmoozing with founders and their new hires, and is probably only practical in major cities with a very active tech meeting scene.
An analysis of a Dutch software business network.
Theoretical analysis
Those with an interest in theory might like to analyse cost-benefit decision-making within software development. Examples of simple analysis+supporting data include:
Analysis of when refactoring becomes cost-effective, and Cost-effectiveness decision for fixing a known coding mistake, and Break even ratios for development investment decisions
Relative sizes of computer companies
How large are computer companies, compared to each other and to companies in other business areas?
Stock market valuation is a one measure of company size, another is a company’s total revenue (i.e., total amount of money brought in by a company’s operations). A company can have a huge revenue, but a low stock market valuation because it makes little profit (because it has to spend an almost equally huge amount to produce that income) and things are not expected to change.
The plot below shows the stock market valuation of IBM/Microsoft/Apple, over time, as a percentage of the valuation of tech companies on the US stock exchange (code+data on Github):
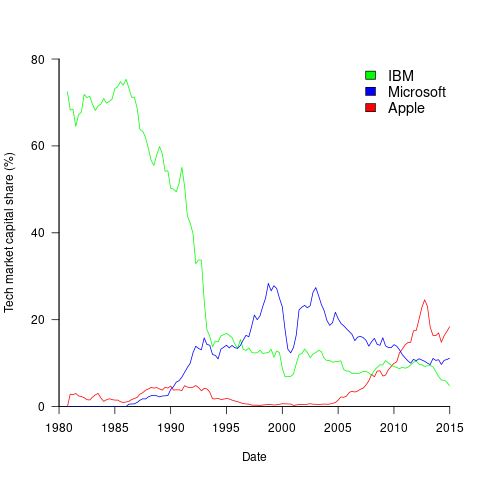
The growth of major tech companies, from the mid-1980s caused IBM’s dominant position to dramatically decline, while first Microsoft, and then Apple, grew to have more dominant market positions.
Is IBM’s decline in market valuation mirrored by a decline in its revenue?
The Fortune 500 was an annual list of the top 500 largest US companies, by total revenue (it’s now a global company list), and the lists from 1955 to 2012 are available via the Wayback Machine. Which of the 1,959 companies appearing in the top 500 lists should be classified as computer companies? Lacking a list of business classification codes for US companies, I asked Chat GPT-4 to classify these companies (responses, which include a summary of the business area). GPT-4 sometimes classified companies that were/are heavy users of computers, or suppliers of electronic components as a computer company. For instance, I consider Verizon Communications to be a communication company.
The plot below shows the ranking of those computer companies appearing within the top 100 of the Fortune 500, after removing companies not primarily in the computer business (code+data):
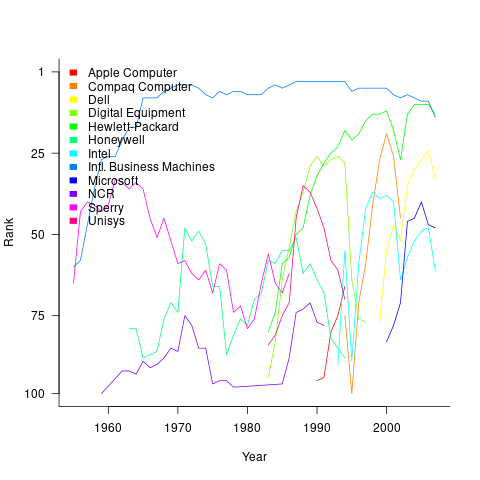
IBM is the uppermost blue line, ranking in the top-10 since the late-1960s. Microsoft and Apple are slowly working their way up from much lower ranks.
These contrasting plots illustrate the fact that while IBM continued to a large company by revenue, its low profitability (and major losses) and the perceived lack of a viable route to sustainable profitability resulted in it having a lower stock market valuation than computer companies with much lower revenues.
Why did organizations fund the creation of the first computers?
What were the events that drove organizations to fund the creation of the first computers?
I suspect that many readers do not appreciate how long scientific/engineering calculations took before electronic computers became available, or the huge number of clerical staff employed to process the paperwork associated with running any sizeable business.
If somebody wanted to know the logarithm of some value, or the sine/cosine of an angle, they looked up the answer in a table. Individuals owned small booklets of tables supplying some level of granularity and number of significant digits. My school boy booklet contains 60-pages of tables, all to five digits of output accuracy, with logarithm supporting four-digit input values and the sine/cosine/tangent tables having an input granularity of hundredth of a degree.
The values in these tables were calculated by human computers; with the following being among the most well known (for more details, see Calculation and Tabulation in the Nineteenth Century: Airy versus Babbage by Doron Swade, and The History of Mathematical Tables: from Sumer to Spreadsheets edited by Campbell-Kelly, Croarken, Flood, and Robson):
- In 1624 Henry Briggs published logarithms for the integer ranges 1-20,000 and 90,001-100,000 (to 14 decimal places), followed some years later by tables of sine and logarithm of sine; in 1628 Adriaan Vlacq publishing tables that filled in the missing values (to 10 decimal places). In 1783 Jurij Vega published a bug-fixed and extended version of Vlacq’s tables.
In 1827 Charles Babbage (that Babbage) published Table of Logarithms of the Natural Numbers from 1 to 10800. These tables were based on corrected versions of these tables, a rigorous nine-stage proofreading process was followed to prevent new mistakes creeping in.
Today, one person can publish A reconstruction of the tables of Briggs’ Arithmetica logarithmica (1624), with an appendix containing 300 pages of calculated values,
- between 1794 and 1799, Gaspard de Prony employed sixty to eighty computers to calculate the logarithms of the integers from 1 to 200,000 to fifteen significant digits (rounding issues sometimes required calculating 25 decimal digits; published in eighteen volumes). Around 400 man-years.
Logarithms and trigonometric functions are very widely used, creating incentives for investing in calculating and publishing tables. While it may be financially worthwhile investing in producing tables for some niche markets (e.g. Life tables for insurance companies), there is an unmet demand that will only be filled by a dramatic drop in the cost of computing simple expressions.
Babbage’s Difference engine was designed to evaluate polynomial expressions and print the results; perfect for publishing tables. While Babbage did not build a Difference engine, starting in 1837, engines based on Babbage’s design were built and sold commercially by the Swede Per Georg Scheutz.
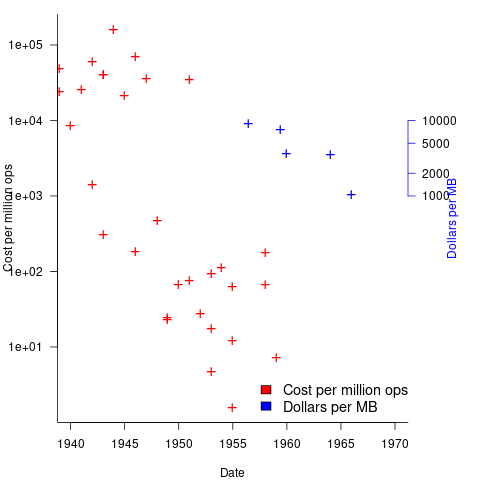
Mechanical calculators improve accuracy and speed the process up. Vacuum tubes are invented in 1904 and become widely used to process analogue signals. World War II created an urgent demand for the results of a variety of time-consuming calculations, e.g., accurate ballistic tables, and valve computers were built. The plot below shows the cost per million operations for manual, mechanical and valve computers (code+data):
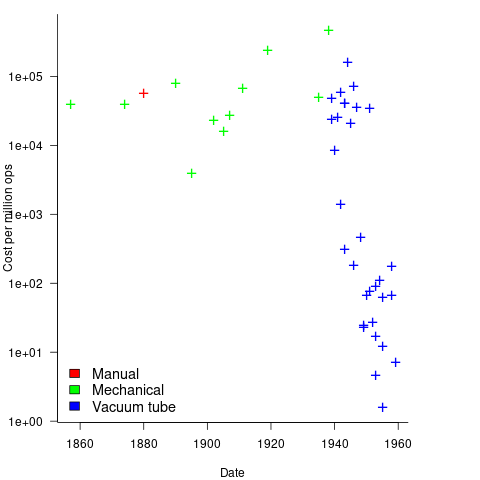
To many observers at the start of the 1950s, the market for electronic computers appeared to be organizations who needed to perform large amounts of scientific/engineering calculation.
Most businesses perform simple calculations on many unrelated values, e.g., banks have to credit/debit the appropriate account when money is deposited/withdrawn. There is no benefit in having a machine that can perform hundreds of calculations per second unless it can be fed data fast enough to keep it busy.
It so happened that, at the start of the 1950s, the US banking system was facing a crisis, the growth in the number of cheques being written meant that it would soon take longer than one day to process all the cheques that arrived in one day. In 1950 Bank of America managed 4.6 million checking accounts, and were opening 23,000 new account per month. Bank of America was then the largest bank in the world, and had a keen interest in continued growth. They funded the development of a bespoke computer system for processing cheques, the ERMA Banking system, which went live in 1959. The plot below shows the number of cheques processed per year by US banks (code+data):
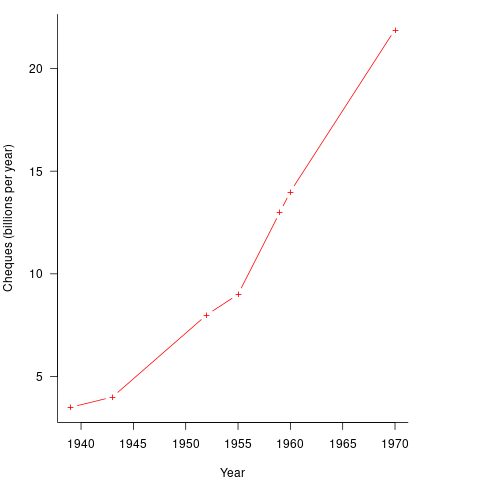
The ERMA system included electronic storage for holding account details, and data entry was speeded up by encoding account details on a magnetic strip included within every cheque.
Businesses are very interested in an integrated combination of input devices plus electronic storage plus compute. There are more commerce oriented businesses than scientific/engineering businesses, and commercial businesses usually have a lot more money to spend, i.e., the real money to be made by selling computers was the business data processing market.
The plot below shows the decreasing cost of hard disc storage (blue, right axis), along with the decreasing computing cost of valve based computers (red, left axis; code+data):
There was a larger business demand to be able to store information electronically, and the hard disc was invented by IBM, roughly 15 years after the first electronic computers.
The very different application demands of data processing and scientific/engineering are reflected in the features supported by the two languages designed in the 1950s, and widely used for the rest of the century: Cobol and Fortran.
Data processing involves simple operations on large quantities of data stored in a potentially huge number of different combinations (the myriad of mechanical point-of-sale terminals stored data in a myriad of different formats, which evolved over time, and the demand for backward compatibility created spaghetti data well before spaghetti code existed). Cobol has extensive functionality supporting the layout and format of input and output data, and simplistic coding constructs.
Scientific/engineering code involves complex calculations on some amount of input. Fortran has extensive functionality supporting program control flow, and relatively basic support for data input/output.
A third major application domain is real-time processing, such as SAGE. However, data on this domain is very hard to find, so it is not discussed.
Analysis of when refactoring becomes cost-effective
In a cost/benefit analysis of deciding when to refactor code, which variables are needed to calculate a good enough result?
This analysis compares the excess time-code of future work against the time-cost of refactoring the code. Refactoring is cost-effective when the reduction in future work time is less than the time spent refactoring. The analysis finds a relationship between work/refactoring time-costs and number of future coding sessions.
Linear, or supra-linear case
Let’s assume that the time needed to write new code grows at a linear, or supra-linear rate, as the amount of code increases (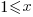
):
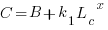
where: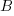 
is the base time for writing new code on a freshly refactored code base, 
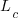is the number of lines of code that have been written since the last refactoring, and 
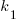and 
are constants to be decided.
The total time spent writing code over 
sessions is:
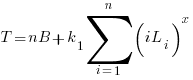
If the same number of new lines is added in every coding session,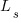 
, and is an integer constant, then the sum has a known closed form, e.g.:
x=1,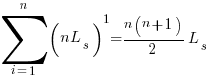 
; x=2,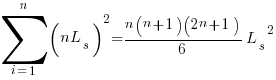 
Let’s assume that the time taken to refactor the code written after sessions is:
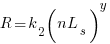
where: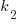 
and 
are constants to be decided.
The reason for refactoring is to reduce the time-cost of subsequent work; if there are no subsequent coding sessions, there is no economic reason to refactor the code. If we assume that after refactoring, the time taken to write new code is reduced to the base cost, 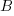, and that we believe that coding will continue at the same rate for at least another 
sessions, then refactoring existing code after sessions is cost-effective when:
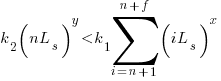
assuming that is much smaller than , setting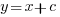 
, and rearranging we get:
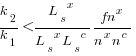
after rearranging we obtain a lower limit on the number of future coding sessions, , that must be completed for refactoring to be cost-effective after session ::
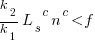
It is expected that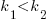 
; the contribution of code size, at the end of every session, in the calculation of 
and 
is equal (i.e.,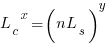 
), and the overhead of adding new code is very unlikely to be less than refactoring all the newly written code.
With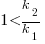 
, 
must be close to zero; otherwise, the likely relatively large value of 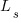(e.g., 100+) would produce surprisingly high values of .
Sublinear case
What if the time overhead of writing new code grows at a sublinear rate, as the amount of code increases?
Various attributes have been found to strongly correlate with the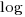 
of lines of code. In this case, the expressions for and become:
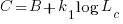
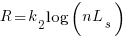
and the cost/benefit relationship becomes:
applying Stirling’s approximation and simplifying (see Exact equations for sums at end of post for details) we get:
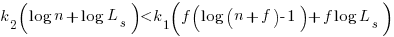
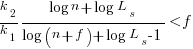
applying the series expansion (for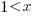 
): 
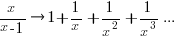, we get
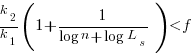
Discussion
What does this analysis of the cost/benefit relationship show that was not obvious (i.e., the relationship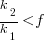 
is obviously true)?
What the analysis shows is that when real-world values are plugged into the full equations, all but two factors have a relatively small impact on the result.
A factor not included in the analysis is that source code has a half-life (i.e., code is deleted during development), and the amount of code existing after sessions is likely to be less than the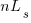 
used in the analysis (see Agile analysis).
As a project nears completion, the likelihood of there being more coding sessions decreases; there is also the every present possibility that the project is shutdown.
The values of 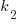and 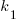encode information on the skill of the developer, the difficulty of writing code in the application domain, and other factors.
Exact equations for sums
The equations for the exact sums, for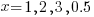 
, are:
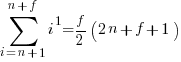
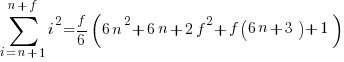
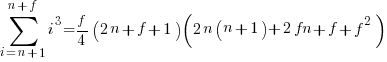
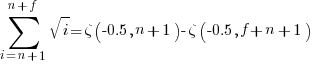, where 
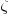is the Hurwitz zeta function.
Sum of a log series: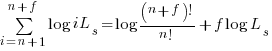 
using Stirling’s approximation we get
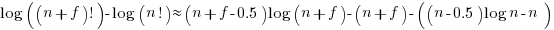
simplifying
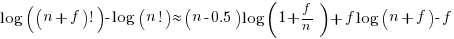
and assuming that is much smaller than gives
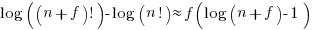
Unneeded requirements implemented in Waterfall & Agile
Software does not wear out, but the world in which it runs evolves. Time and money is lost when, after implementing a feature in software, customer feedback is that the feature is not needed.
How do Waterfall and Agile implementation processes compare in the number of unneeded feature/requirements that they implement?
In a Waterfall process, a list of requirements is created and then implemented. The identity of ‘dead’ requirements is not known until customers start using the software, which is not until it is released at the end of development.
In an Agile process, a list of requirements is used to create a Minimal Viable Product, which is released to customers. An iterative development processes, driven by customer feedback, implements requirements, and makes frequent releases to customers, which reduces the likelihood of implementing known to be ‘dead’ requirements. Previously implemented requirements may be discovered to have become ‘dead’.
An analysis of the number of ‘dead’ requirements implemented by the two approaches appears at the end of this post.
The plot below shows the number of ‘dead’ requirements implemented in a project lasting a given number of working days (blue/red) and the difference between them (green), assuming that one requirement is implemented per working day, with the discovery after 100 working days that a given fraction of implemented requirements are not needed, and the number of requirements in the MVP is assumed to be small (fractions 0.5, 0.1, and 0.05 shown; code):
The values calculated using one requirement implemented per day scales linearly with requirements implemented per day.
By implementing fewer ‘dead’ requirements, an Agile project will finish earlier (assuming it only implements all the needed requirements of a Waterfall approach, and some subset of the ‘dead’ requirements). However, unless a project is long-running, or has a high requirements’ ‘death’ rate, the difference may not be compelling.
I’m not aware of any data on rate of discovery of ‘dead’ implemented requirements (there is some on rate of discovery of new requirements); as always, pointers to data most welcome.
The Waterfall projects I am familiar with, plus those where data is available, include some amount of requirement discovery during implementation. This has the potential to reduce the number of ‘dead’ implemented requirements, but who knows by how much.
As the size of Minimal Viable Product increases to become a significant fraction of the final software system, the number of fraction of ‘dead’ requirements will approach that of the Waterfall approach.
There are other factors that favor either Waterfall or Agile, which are left to be discussed in future posts.
The following is an analysis of Waterfall/Agile requirements’ implementation.
Define:
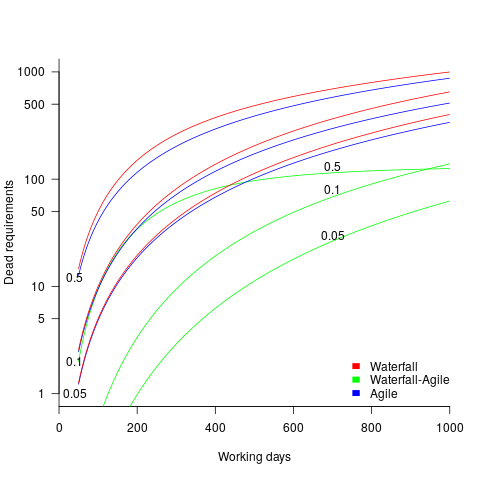
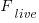is the fraction of requirements per day that remain relevant to customers. This value is likely to be very close to one, e.g., 
.
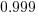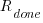requirements implemented per working day.
Waterfall
The implementation of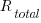 
requirements takes 
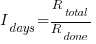days, and the number of implemented ‘dead’ requirements is (assuming that the no ‘dead’ requirements were present at the end of the requirements gathering phase):
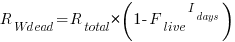
As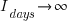 
effectively all implemented requirements are ‘dead’.
Agile
The number of implemented ‘live’ requirements on day is given by:
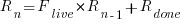
with the initial condition that the number of implemented requirements at the start of the first day of iterative development is the number of requirements implemented in the Minimum Viable Product, i.e.,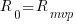 
.
Solving this difference equation gives the number of ‘live’ requirements on day :
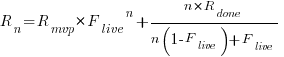
as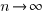 
, 
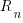approaches to its maximum value of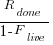 
Subtracting the number of ‘live’ requirements from the total number of requirements implemented gives:
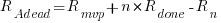
or
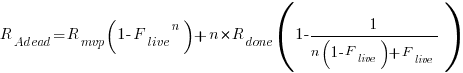
or
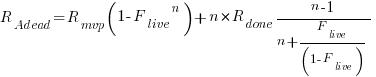
as 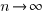effectively all implemented requirements are ‘dead’, because the number of ‘live’ requirements cannot exceed a known maximum.
Update
The paper A software evolution experiment found that in a waterfall project, 40% of modules in the delivered system were not required.
Optimal sizing of a product backlog
Developers working on the implementation of a software system will have a list of work that needs to be done, a to-do list, known as the product backlog in Agile.
The Agile development process differs from the Waterfall process in that the list of work items is intentionally incomplete when coding starts (discovery of new work items is an integral part of the Agile process). In a Waterfall process, it is intended that all work items are known before coding starts (as work progresses, new items are invariably discovered).
Complaints are sometimes expressed about the size of a team’s backlog, measured in number of items waiting to be implemented. Are these complaints just grumblings about the amount of work outstanding, or is there an economic cost that increases with the size of the backlog?
If the number of items in the backlog is too low, developers may be left twiddling their expensive thumbs because they have run out of work items to implement.
A parallel is sometimes drawn between items waiting to be implemented in a product backlog and hardware items in a manufacturer’s store waiting to be checked-out for the production line. Hardware occupies space on a shelf, a cost in that the manufacturer has to pay for the building to hold it; another cost is the interest on the money spent to purchase the items sitting in the store.
For over 100 years, people have been analyzing the problem of the optimum number of stock items to order, and at what stock level to place an order. The economic order quantity gives the optimum number of items to reorder,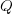 
(the derivation assumes that the average quantity in stock is 
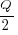), it is given by:
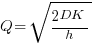, where 
is the quantity consumed per year, 
is the fixed cost per order (e.g., cost of ordering, shipping and handling; not the actual cost of the goods),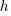 
is the annual holding cost per item.
What is the likely range of these values for software?
- is around 1,000 per year for a team of ten’ish people working on multiple (related) projects; based on one dataset,
- is the cost associated with the time taken to gather the requirements, i.e., the items to add to the backlog. If we assume that the time taken to gather an item is less than the time taken to implement it (the estimated time taken to implement varies from hours to days), then the average should be less than an hour or two,
- : While the cost of a post-it note on a board, or an entry in an online issue tracking system, is effectively zero, there is the time cost of deciding which backlog items should be implemented next, or added to the next Sprint.
If the backlog starts with
items, and it takes 
seconds to decide whether a given item should be implemented next, and is the fraction of items scanned before one is selected: the average decision time per item is: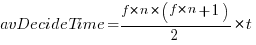 
seconds. For example, if 
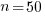, pulling some numbers out of the air, 
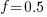, and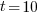 
, then 
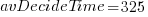, or 5.4 minutes.The Scrum approach of selecting a subset of backlog items to completely implement in a Sprint has a much lower overhead than the one-at-a-time approach.
If we assume that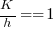 
, then 
.
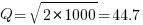An ‘order’ for 45 work items might make sense when dealing with clients who have formal processes in place and are not able to be as proactive as an Agile developer might like, e.g., meetings have to be scheduled in advance, with minutes circulated for agreement.
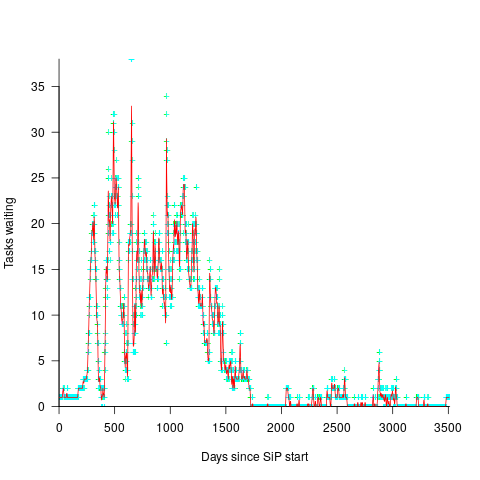
In a more informal environment, with close client contacts, work items are more likely to trickle in or appear in small batches. The SiP dataset came from such an environment. The plot below shows the number of tasks in the backlog of the SiP dataset, for each day (blue/green) and seven-day rolling average (red) (code+data):
Evolution of the DORA metrics
There is a growing buzz around the DORA metrics. Where did the DORA metrics come from, what are they, and are they useful?
The company DevOps Research and Assessment LLC (DORA) was founded by Nicole Forsgren, Jez Humble, and Gene Kim in 2016, and acquired by Google in 2018. DevOps is a role that combines software development (Dev) and IT operations (Ops).
The original ideas behind the DORA metrics are described in the 2015 paper DevOps: Profiles in ITSM Performance and Contributing Factors, by Forsgren and Humble. The more well known Accelerate book, published in 2018, is an evangelistic reworking of the material, plus some business platitudes extolling the benefits of using a lean process.
The 2015 paper approaches the metric selection process from the perspective of reducing business costs, and uses a data driven approach. This is how metric selection should be done, and for the first seven or eight pages I was cheering the authors on. The validity of a data driven approaches depends on the reliability of the data and its applicability to the questions being addressed. I don’t think that the reliability of the data used is sufficient to support the conclusions being drawn from it. The data used is the survey results behind the Puppet Labs 2015 State of DevOps Report; the 2018 book included data from the 2016 and 2017 State of DevOps reports.
Between 2015-2018, DORA is more a way of doing DevOps than a collection of metrics to calculate. The theory is based on ideas from the Economic Order Quantity model; this model is used in inventory management to calculate the number of items that should be held in stock, to meet production demand, such that stock holding costs plus item reordering costs are minimised (when the number of items in stock falls below some value, there is an optimum number of items to reorder to replenish stocks).
The DORA mapping of the Economic Order Quantity model to DevOps employs a rather liberal interpretation of the concepts involved. There are three fundamental variables:
- Batch size: the quantity of additions, modifications and deletions of anything that could have an effect on IT services, e.g., changes to code or configuration files,
- Holding cost: the lost opportunity cost of not deploying work that has been done, e.g., lost business because a feature is not available or waste because an efficiency improvement is not used. Cognitive capitalism also has the lost opportunity cost of not learning about the impact of an update on the ecosystem,
- Transaction cost: the cost of building, testing and deploying to production a completed batch.
The aim is to minimise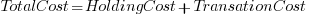 
.
So far, so good and reasonable.
Now the details; how do we measure batch size, holding cost and transaction cost?
DORA does not measure these quantities (the paper points out that deployment frequency could be treated as a proxy for batch size, in that as deployment frequency goes to infinity batch size goes to zero). The terms holding cost and transaction cost do not appear in the 2018 book.
Having mapped Economic Order Quantity variables to software, the 2015 paper pivots and maps these variables to a Lean manufacturing process (the 2018 book focuses on Lean). Batch size is now deployment frequency, and higher is better.
Ok, let’s follow the pivoted analysis of Lean ideas applied to software. The 2015 paper uses cluster analysis to find patterns in the 2015 State of DevOps survey data. I have not seen any of the data, or even the questions asked; the description of the analysis is rather sketchy (I imagine it is similar to that used by Forsgren in her PhD thesis on a different dataset). The report published by Puppet Labs analyses the data using linear regression and partial least squares.
Three IT performance profiles are characterized (High, Medium and Low). Why three and not, say, four or five? The papers simply says that three ’emerged’.
The analysis of the Puppet Labs 2015 survey data (6k+ responses) essentially takes the form of listing differences in values of various characteristics between High/Medium/Low teams; responses came from “technical professionals of all specialities involved in DevOps”. The analysis in the 2018 book discussed some of the between year differences.
My experience of asking hundreds of people for data is that most don’t have any. I suspect this is true of those who answered the Puppet Labs surveys, and that answers are guestimates.
The fact that the accuracy of analysis of the survey data is poor does not really matter, because DORA pivots again.
This pivot switches to organizational metrics (from team metrics), becomes purely production focused (very appropriate for DevOps), introduces an Elite profile, and focuses on four key metrics; the following is adapted from Google:
- Deployment Frequency: How often an organization successfully releases to production,
- Lead Time for Changes: The amount of time it takes a commit to get into production,
- Change Failure Rate: The percentage of deployments causing a failure in production,
- Mean time to repair (MTTR): How long it takes an organization to recover from a failure in production.
Are these four metrics useful?
To somebody with zero DevOps experience (i.e., me) they look useful. The few DevOps people I have spoken to are talking about them but not using them (not least because they don’t have the data required).
The characteristics of the Elite/High/Medium/Low profiles reflects Google’s DevOps business interests. Companies offering an online service at a national scale want to quickly respond to customer demand, continuously deploy, and quickly recover from service outages.
There are companies where it makes business sense for DevOps deployments to occur much less frequently than at Google. I also know companies who would love to have deployment rates within an order of magnitude of Google’s, but cannot even get close without a significant restructuring of their build and deployment infrastructure.
Complex software makes economic sense
Economic incentives motivate complexity as the common case for software systems.
When building or maintaining existing software, often the quickest/cheapest approach is to focus on the features/functionality being added, ignoring the existing code as much as possible. Yes, the new code may have some impact on the behavior of the existing code, and as new features/functionality are added it becomes harder and harder to predict the impact of the new code on the behavior of the existing code; in particular, is the existing behavior unchanged.
Software is said to have an attribute known as complexity; what is complexity? Many definitions have been proposed, and it’s not unusual for people to use multiple definitions in a discussion. The widely used measures of software complexity all involve counting various attributes of the source code contained within individual functions/methods (e.g., McCabe cyclomatic complexity, and Halstead); they are all highly correlated with lines of code. For the purpose of this post, the technical details of a definition are glossed over.
Complexity is often given as the reason that software is difficult to understand; difficult in the sense that lots of effort is required to figure out what is going on. Other causes of complexity, such as the domain problem being solved, or the design of the system, usually go unmentioned.
The fact that complexity, as a cause of requiring more effort to understand, has economic benefits is rarely mentioned, e.g., the effort needed to actively use a codebase is a barrier to entry which allows those already familiar with the code to charge higher prices or increases the demand for training courses.
One technique for reducing the complexity of a system is to redesign/rework its implementation, from a system/major component perspective; known as refactoring in the software world.
What benefit is expected to be obtained by investing in refactoring? The expected benefit of investing in redesign/rework is that a reduction in the complexity of a system will reduce the subsequent costs incurred, when adding new features/functionality.
What conditions need to be met to make it worthwhile making an investment, 
, to reduce the complexity, , of a software system?
Let’s assume that complexity increases the cost of adding a feature by some multiple (greater than one). The total cost of adding features is:
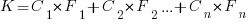
where: 
is the system complexity when feature 
is added, and 
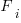is the cost of adding this feature if no complexity is present.
, 
, … 
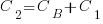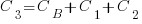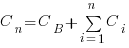
where: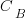 
is the base complexity before adding any new features.
Let’s assume that an investment, , is made to reduce the complexity from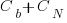 
(with 
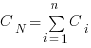) to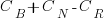 
, where 
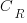is the reduction in the complexity achieved. The minimum condition for this investment to be worthwhile is that:
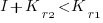or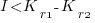 
where: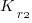 
is the total cost of adding new features to the source code after the investment, and 
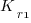is the total cost of adding the same new features to the source code as it existed immediately prior to the investment.
Resetting the feature count back to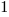 
, we have:
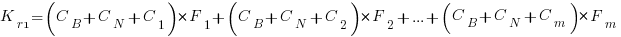
and
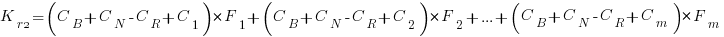
and the above condition becomes:
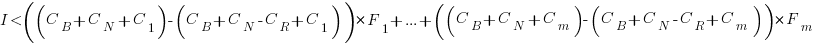
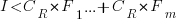
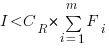
The decision on whether to invest in refactoring boils down to estimating the reduction in complexity likely to be achieved (as measured by effort), and the expected cost of future additions to the system.
Software systems eventually stop being used. If it looks like the software will continue to be used for years to come (software that is actively used will have users who want new features), it may be cost-effective to refactor the code to returning it to a less complex state; rinse and repeat for as long as it appears cost-effective.
Investing in software that is unlikely to be modified again is a waste of money (unless the code is intended to be admired in a book or course notes).
Study of developers for the cost of a phase I clinical drug trial
For many years now, I have been telling people that software researchers need to be more ambitious and apply for multi-million pound/dollar grants to run experiments in software engineering. After all, NASA spends a billion or so sending a probe to take some snaps of a planet and astronomers lobby for $100million funding for a new telescope.
What kind of experimental study might be run for a few million pounds (e.g., the cost of a Phase I clinical drug trial)?
Let’s say that each experiment involves a team of professional developers implementing a software system; call this a Project. We want the Project to be long enough to be realistic, say a week.
Different people exhibit different performance characteristics, and the experimental technique used to handle this is to have multiple teams independently implement the same software system. How many teams are needed? Fifteen ought to be enough, but more is better.
Different software systems contain different components that make implementation easier/harder for those involved. To remove single system bias, a variety of software systems need to be used as Projects. Fifteen distinct Projects would be great, but perhaps we can get away with five.
How many developers are on a team? Agile task estimation data shows that most teams are small, i.e., mostly single person, with two and three people teams making up almost all the rest.
If we have five teams of one person, five of two people, and five of three people, then there are 15 teams and 30 people.
How many people will be needed over all Projects?
15 teams (30 people) each implementing one Project 5 Projects, which will require 5*30=150 people (5*15=75 teams) |
How many person days are likely to be needed?
If a 3-person team takes a week (5 days), a 2-person team will take perhaps 7-8 days. A 1-person team might take 9-10 days.
The 15 teams will consume 5*3*5+5*2*7+5*1*9=190 person days The 5 Projects will consume 5*190=950 person days |
How much is this likely to cost?
The current average daily rate for a contractor in the UK is around £500, giving an expected cost of 190*500=£475,000 to hire the experimental subjects. Venue hire is around £40K (we want members of each team to be co-located).
The above analysis involves subjects implementing one Project. If, say, each subject implements two, three or four Projects, one after the other, the cost is around £2million, i.e., the cost of a Phase I clinical drug trial.
What might we learn from having subjects implement multiple Projects?
Team performance depends on the knowledge and skill of its members, and their ability to work together. Data from these experiments would be the first of their kind, and would provide realistic guidance on performance factors such as: impact of team size; impact of practice; impact of prior experience working together; impact of existing Project experience. The multiple implementations of the same Project created provide a foundation for measuring expected reliability and theories of N-version programming.
A team of 1 developer will take longer to implement a Project than a team of 2, who will take longer than a team of 3.
If 20 working days is taken as the ballpark period over which a group of subjects are hired (i.e., a month), there are six team size sequences that one subject could work (A to F below); where individual elapsed time is close to 20 days (team size 1 is 10 days elapsed, team size 2 is 7.5 days, team size 3 is 5 days).
Team size A B C D E F
1 twice once once
2 once thrice once
3 twice twice four |
The cost of hiring subjects+venue+equipment+support for such a study is likely to be at least £1,900,000.
If the cost of beta testing, venue hire and research assistants (needed during experimental runs) is included, the cost is close to £2.75 million.
Might it be cheaper and simpler to hire, say, 20-30 staff from a medium size development company? I chose a medium-sized company because we would be able to exert some influence over developer selection and keeping the same developers involved. The profit from 20-30 people for a month is not enough to create much influence within a large company, and a small company would not want to dedicate a large percentage of its staff for a solid month.
Beta testing is needed to validate both the specifications for each Project and that it is possible to schedule individuals to work in a sequence of teams over a month (individual variations in performance create a scheduling nightmare).
Recent Comments