Archive
Unneeded requirements implemented in Waterfall & Agile
Software does not wear out, but the world in which it runs evolves. Time and money is lost when, after implementing a feature in software, customer feedback is that the feature is not needed.
How do Waterfall and Agile implementation processes compare in the number of unneeded feature/requirements that they implement?
In a Waterfall process, a list of requirements is created and then implemented. The identity of ‘dead’ requirements is not known until customers start using the software, which is not until it is released at the end of development.
In an Agile process, a list of requirements is used to create a Minimal Viable Product, which is released to customers. An iterative development processes, driven by customer feedback, implements requirements, and makes frequent releases to customers, which reduces the likelihood of implementing known to be ‘dead’ requirements. Previously implemented requirements may be discovered to have become ‘dead’.
An analysis of the number of ‘dead’ requirements implemented by the two approaches appears at the end of this post.
The plot below shows the number of ‘dead’ requirements implemented in a project lasting a given number of working days (blue/red) and the difference between them (green), assuming that one requirement is implemented per working day, with the discovery after 100 working days that a given fraction of implemented requirements are not needed, and the number of requirements in the MVP is assumed to be small (fractions 0.5, 0.1, and 0.05 shown; code):
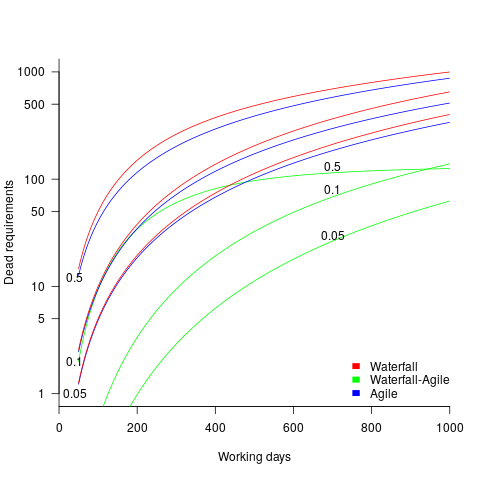
The values calculated using one requirement implemented per day scales linearly with requirements implemented per day.
By implementing fewer ‘dead’ requirements, an Agile project will finish earlier (assuming it only implements all the needed requirements of a Waterfall approach, and some subset of the ‘dead’ requirements). However, unless a project is long-running, or has a high requirements’ ‘death’ rate, the difference may not be compelling.
I’m not aware of any data on rate of discovery of ‘dead’ implemented requirements (there is some on rate of discovery of new requirements); as always, pointers to data most welcome.
The Waterfall projects I am familiar with, plus those where data is available, include some amount of requirement discovery during implementation. This has the potential to reduce the number of ‘dead’ implemented requirements, but who knows by how much.
As the size of Minimal Viable Product increases to become a significant fraction of the final software system, the number of fraction of ‘dead’ requirements will approach that of the Waterfall approach.
There are other factors that favor either Waterfall or Agile, which are left to be discussed in future posts.
The following is an analysis of Waterfall/Agile requirements’ implementation.
Define:
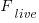 is the fraction of requirements per day that remain relevant to customers. This value is likely to be very close to one, e.g.,
is the fraction of requirements per day that remain relevant to customers. This value is likely to be very close to one, e.g., 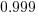 .
.
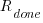 requirements implemented per working day.
requirements implemented per working day.
Waterfall
The implementation of 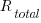 requirements takes
requirements takes 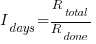 days, and the number of implemented ‘dead’ requirements is (assuming that the no ‘dead’ requirements were present at the end of the requirements gathering phase):
days, and the number of implemented ‘dead’ requirements is (assuming that the no ‘dead’ requirements were present at the end of the requirements gathering phase):
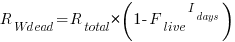
As 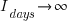 effectively all implemented requirements are ‘dead’.
effectively all implemented requirements are ‘dead’.
Agile
The number of implemented ‘live’ requirements on day  is given by:
is given by:
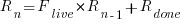
with the initial condition that the number of implemented requirements at the start of the first day of iterative development is the number of requirements implemented in the Minimum Viable Product, i.e., 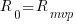 .
.
Solving this difference equation gives the number of ‘live’ requirements on day  :
:
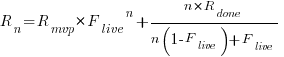
as 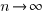 ,
, 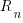 approaches to its maximum value of
approaches to its maximum value of 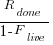
Subtracting the number of ‘live’ requirements from the total number of requirements implemented gives:
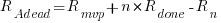
or
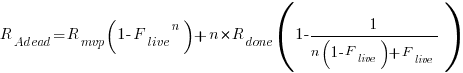
or
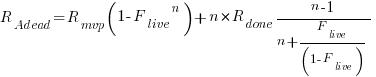
as 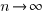 effectively all implemented requirements are ‘dead’, because the number of ‘live’ requirements cannot exceed a known maximum.
effectively all implemented requirements are ‘dead’, because the number of ‘live’ requirements cannot exceed a known maximum.
Update
The paper A software evolution experiment found that in a waterfall project, 40% of modules in the delivered system were not required.
Stochastic rounding reemerges
Just like integer types, floating-point types are capable of representing a finite number of numeric values. An important difference between integer and floating types is that the result of arithmetic and relational operations using integer types is exactly representable in an integer type (provided they don’t overflow), while the result of arithmetic operations using floating types may not be exactly representable in the corresponding floating type.
When the result of a floating-point operation cannot be exactly represented, it is rounded to a value that can be represented. Rounding modes include: round to nearest (the default for IEEE-754), round towards zero (i.e., truncated), round up (i.e., towards 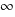 ), round down (i.e., towards
), round down (i.e., towards 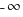 ), and round to even. The following is an example of round to nearest:
), and round to even. The following is an example of round to nearest:
123456.7 = 1.234567 × 10^5
101.7654 = 0.001017654 × 10^5
Adding
= 1.235584654 × 10^5
Round to nearest
= 1.235585 × 10^5 |
There is another round mode, one implemented in the 1950s, which faded away but could now be making a comeback: Stochastic rounding. As the name suggests, every round up/down decision is randomly chosen; a Google patent makes some claims about where the entropy needed for randomness can be obtained, and Nvidia also make some patent claims).
From the developer perspective, stochastic rounding has a very surprising behavior, which is not present in the other IEEE rounding modes; stochastic rounding is not monotonic. For instance: z < x+y does not imply that 0<(x+y)-z, because x+y may be close enough to z to have a 50% chance of being rounded to one of z or the next representable value greater than z, and in the comparison against zero the rounded value of (x+y) has an uncorrelated probability of being equal to z (rather than the next representable greater value).
For some problems, stochastic rounding avoids undesirable behaviors that can occur when round to nearest is used. For instance, round to nearest can produce correlated rounding errors that cause systematic error growth (by definition, stochastic rounding is uncorrelated); a behavior that has long been known to occur when numerically solving differential equations. The benefits of stochastic rounding are obtained for calculations involving long chains of calculations; the rounding error of the result of  operations is guaranteed to be proportional to
operations is guaranteed to be proportional to 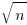 , i.e., just like a 1-D random walk, which is not guaranteed for round to nearest.
, i.e., just like a 1-D random walk, which is not guaranteed for round to nearest.
While stochastic rounding has been supported by some software packages for a while, commercial hardware support is still rare, with Graphcore's Intelligence Processing Unit being one. There are some research chips supporting stochastic rounding, e.g., Intel's Loihi.
What applications, other than solving differential equations, involve many long chain calculations?
Training of machine learning models can consume many cpu hours/days; the calculation chains just go on and on.
Machine learning is considered to be a big enough market for hardware vendors to support half-precision floating-point. The performance advantages of half-precision floating-point are large enough to attract developers to reworking code to make use of them.
Is the accuracy advantage of stochastic rounding a big enough selling point that hardware vendors will provide the support needed to attract a critical mass of developers willing to rework their code to take advantage of improved accuracy?
It's possible that the intrinsically fuzzy nature of many machine learning applications swamps the accuracy advantage that stochastic rounding can have over round to nearest, out-weighing the costs of supporting it.
The ecosystem of machine learning based applications is still evolving rapidly, and we will have to wait and see whether stochastic rounding becomes widely used.
Some human biases in conditional reasoning
Tracking down coding mistakes is a common developer activity (for which training is rarely provided).
Debugging code involves reasoning about differences between the actual and expected output produced by particular program input. The goal is to figure out the coding mistake, or at least narrow down the portion of code likely to contain the mistake.
Interest in human reasoning dates back to at least ancient Greece, e.g., Aristotle and his syllogisms. The study of the psychology of reasoning is very recent; the field was essentially kick-started in 1966 by the surprising results of the Wason selection task.
Debugging involves a form of deductive reasoning known as conditional reasoning. The simplest form of conditional reasoning involves an input that can take one of two states, along with an output that can take one of two states. Using coding notation, this might be written as:
if (p) then q if (p) then !q if (!p) then q if (!p) then !q |
The notation used by the researchers who run these studies is a 2×2 contingency table (or conditional matrix):
OUTPUT
1 0
1 A B
INPUT
0 C D |
where: A, B, C, and D are the number of occurrences of each case; in code notation, p is the input and q the output.
The fertilizer-plant problem is an example of the kind of scenario subjects answer questions about in studies. Subjects are told that a horticultural laboratory is testing the effectiveness of 31 fertilizers on the flowering of plants; they are told the number of plants that flowered when given fertilizer (A), the number that did not flower when given fertilizer (B), the number that flowered when not given fertilizer (C), and the number that did not flower when not given any fertilizer (D). They are then asked to evaluate the effectiveness of the fertilizer on plant flowering. After the experiment, subjects are asked about any strategies they used to make judgments.
Needless to say, subjects do not make use of the available information in a way that researchers consider to be optimal, e.g., Allan’s  index
index 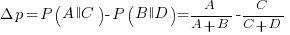 (sorry about the double,
(sorry about the double, 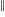 , rather than single, vertical lines).
, rather than single, vertical lines).
What do we know after 40+ years of active research into this basic form of conditional reasoning?
The results consistently find, for this and other problems, that the information A is given more weight than B, which is given by weight than C, which is given more weight than D.
That information provided by A and B is given more weight than C and D is an example of a positive test strategy, a well-known human characteristic.
Various models have been proposed to ‘explain’ the relative ordering of information weighting:  , e.g., that subjects have a bias towards sufficiency information compared to necessary information.
, e.g., that subjects have a bias towards sufficiency information compared to necessary information.
Subjects do not always analyse separate contingency tables in isolation. The term blocking is given to the situation where the predictive strength of one input is influenced by the predictive strength of another input (this process is sometimes known as the cue competition effect). Debugging is an evolutionary process, often involving multiple test inputs. I’m sure readers will be familiar with the situation where the output behavior from one input motivates a misinterpretation of the behaviour produced by a different input.
The use of logical inference is a commonly used approach to the debugging process (my suggestions that a statistical approach may at times be more effective tend to attract odd looks). Early studies of contingency reasoning were dominated by statistical models, with inferential models appearing later.
Debugging also involves causal reasoning, i.e., searching for the coding mistake that is causing the current output to be different from that expected. False beliefs about causal relationships can be a huge waste of developer time, and research on the illusion of causality investigates, among other things, how human interpretation of the information contained in contingency tables can be ‘de-biased’.
The apparently simple problem of human conditional reasoning over two variables, each having two states, has proven to be a surprisingly difficult to model. It is tempting to think that the performance of professional software developers would be closer to the ideal, compared to the typical experimental subject (e.g., psychology undergraduates or Mturk workers), but I’m not sure whether I would put money on it.
Evidence-based Software Engineering book: two years later
Two years ago, my book Evidence-based Software Engineering: based on the publicly available data was released. The first two weeks saw 0.25 million downloads, and 0.5 million after six months. The paperback version on Amazon has sold perhaps 20 copies.
How have the book contents fared, and how well has my claim to have discussed all the publicly available software engineering data stood up?
The contents have survived almost completely unscathed. This is primarily because reader feedback has been almost non-existent, and I have hardly spent any time rereading it.
In the last two years I have discovered maybe a dozen software engineering datasets that would have been included, had I known about them, and maybe another dozen non-software related datasets that could have been included in the Human behavior/Cognitive capitalism/Ecosystems/Reliability chapters. About half of these have been the subject of blog posts (links below), with the others waiting to be covered.
Each dataset provides a sliver of insight into the much larger picture that is software engineering; joining the appropriate dots, by analyzing multiple datasets, can provide a larger sliver of insight into the bigger picture. I have not spent much time attempting to join dots, but have joined a few tiny ones, and a few that are not so small, e.g., Estimating using a granular sequence of values and Task backlog waiting times are power laws.
I spent the first year, after the book came out, working through the backlog of tasks that had built up during the 10-years of writing. The second year was mostly dedicated to trying to find software project data (including joining Twitter), and reading papers at a much reduced rate.
The plot below shows the number of monthly downloads of the A4 and mobile friendly pdfs, along with the average kbytes per download (code+data):
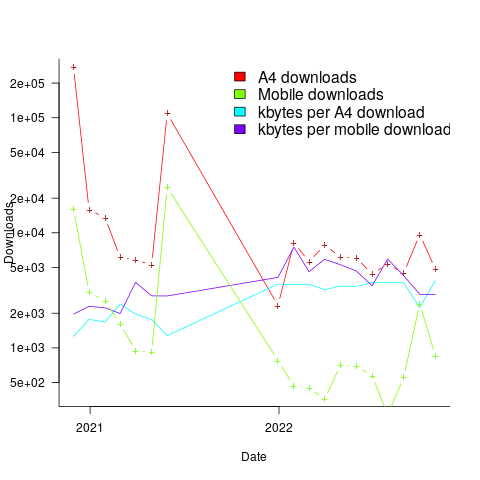
The monthly averages for 2022 are around 6K A4 and 700 mobile friendly pdfs.
I have been averaging one in-person meetup per week in London. Nearly everybody I tell about the book has not previously heard of it.
The following is a list of blog posts either analyzing existing data or discussing/analyzing new data.
Introduction
analysis: Software effort estimation is mostly fake research
analysis: Moore’s law was a socially constructed project
Human behavior
data (reasoning): The impact of believability on reasoning performance
data: The Approximate Number System and software estimating
data (social conformance): How large an impact does social conformity have on estimates?
data (anchoring): Estimating quantities from several hundred to several thousand
data: Cognitive effort, whatever it might be
Ecosystems
data: Growth in number of packages for widely used languages
data: Analysis of a subset of the Linux Counter data
data: Overview of broad US data on IT job hiring/firing and quitting
Projects
analysis: Delphi and group estimation
analysis: The CESAW dataset: a brief introduction
analysis: Parkinson’s law, striving to meet a deadline, or happenstance?
analysis: Evaluating estimation performance
analysis: Complex software makes economic sense
analysis: Cost-effectiveness decision for fixing a known coding mistake
analysis: Optimal sizing of a product backlog
analysis: Evolution of the DORA metrics
analysis: Two failed software development projects in the High Court
data: Pomodoros worked during a day: an analysis of Alex’s data
data: Multi-state survival modeling of a Jira issues snapshot
data: Over/under estimation factor for ‘most estimates’
data: Estimation accuracy in the (building|road) construction industry
data: Rounding and heaping in non-software estimates
data: Patterns in the LSST:DM Sprint/Story-point/Story ‘done’ issues
data: Shopper estimates of the total value of items in their basket
Reliability
analysis: Most percentages are more than half
Statistical techniques
Fitting discontinuous data from disparate sources
Testing rounded data for a circular uniform distribution
Post 2020 data
Pomodoros worked during a day: an analysis of Alex’s data
Impact of number of files on number of review comments
Finding patterns in construction project drawing creation dates
A study of deceit when reporting information in a known context
A variety of conflicting factors intrude when attempting to form an impartial estimate of the resources needed to perform a task. The customer/manager, asking for the estimate, wants to hear a low value, creating business/social pressure to underestimate; overestimating increases the likelihood of completing the task within budget.
A study by Oey, Schachner and Vul investigated the strategic reasoning for deception/lying in a two-person game.
A game involved a Sender and Receiver, with the two players alternating between the roles. The game started with both subjects seeing a picture of a box containing red and blue marbles (the percentage of red marbles was either 20%, 50%, or 80%). Ten marbles were randomly selected from this ‘box’, and shown to the Sender. The Sender was asked to report to the Receiver the number of red marbles appearing in the random selection,  (there was an incentive to report higher/lower, and punishment for being caught being inaccurate). The Receiver could accept or reject the number of red balls reported by the Sender. In the actual experiment, unknown to the human subjects, one of every game’s subject pair was always played by a computer. Every subject played 100 games.
(there was an incentive to report higher/lower, and punishment for being caught being inaccurate). The Receiver could accept or reject the number of red balls reported by the Sender. In the actual experiment, unknown to the human subjects, one of every game’s subject pair was always played by a computer. Every subject played 100 games.
In the inflate condition: If the Receiver accepted the report, the Sender gained  points, and the Receiver gained
points, and the Receiver gained 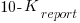 points.
points.
If the Receiver rejected the report, then:
- if the Sender’s report was accurate (i.e.,
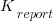 ==
== 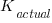 ), the Sender gained
), the Sender gained 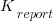 points, and the Receiver gained
points, and the Receiver gained  points (i.e., a -5 point penalty),
points (i.e., a -5 point penalty), - if the Sender’s report was not accurate, the Receiver gained 5 points, and the Sender lost 5 points.
In the deflate condition: The points awarded to the Sender was based on the number of blue balls in the sample, and the points awarded to the Received was based on the number of red balls in the sample (i.e., the Sender had in incentive to report fewer red balls).
The plot below shows the mean rate of deceit (i.e., the fraction of a subject’s reports where  , averaged over all 116 subject’s mean) for a given number of red marbles actually seen by the Sender; vertical lines show one standard deviation, calculated over the mean of all subjects (code+data):
, averaged over all 116 subject’s mean) for a given number of red marbles actually seen by the Sender; vertical lines show one standard deviation, calculated over the mean of all subjects (code+data):

Subjects have some idea of the percentage of red/blue balls, and are aware that their opponent has a similar idea.
The wide variation in the fraction of reports where a subject reported a value greater than the number of marbles seen, is likely caused by variation in subject level of risk aversion. Some subjects may have decided to reduce effort by always accurately reporting, while others may have tried to see how much they could get away with.
The wide variation is particularly noticeable in the case of a box containing 80% red. If a Sender’s random selection contains few reds, then the Sender can feel confident reporting to have seen more.
The general pattern shows subjects being more willing to increase the reported number when they are supplied with few.
There is a distinct change of behavior when half of the sample contains more than five red marbles. In this situation, subjects may be happy to have been dealt a good hand, and are less inclined to risk losing 5-points for less gain.
Estimating involves considering more factors than the actual resources likely to be needed to implement the task; the use of round numbers is one example. This study is one of few experimental investigations of numeric related deception. The use of students having unknown motivation is far from ideal, but they are better than nothing.
When estimating in a team context, there is an opportunity to learn about the expectations of others and the consequences of over/under estimating. An issue for another study 🙂
Studying the lifetime of Open source
A software system can be said to be dead when the information needed to run it ceases to be available.
Provided the necessary information is available, plus time/money, no software ever has to remain dead, hardware emulators can be created, support libraries can be created, and other necessary files cobbled together.
In the case of software as a service, the vendor may simply stop supplying the service; after which, in my experience, critical components of the internal service ecosystem soon disperse and are forgotten about.
Users like the software they use to be actively maintained (i.e., there are one or more developers currently working on the code). This preference is culturally driven, in that we are living through a period in which most in-use software systems are actively maintained.
Active maintenance is perceived as a signal that the software has some amount of popularity (i.e., used by other people), and is up-to-date (whatever that means, but might include supporting the latest features, or problem reports are being processed; neither of which need be true). Commercial users like actively maintained software because it enables the option of paying for any modifications they need to be made.
Software can be a zombie, i.e., neither dead or alive. Zombie software will continue to work for as long as the behavior of its external dependencies (e.g., libraries) remains sufficiently the same.
Active maintenance requires time/money. If active maintenance is required, then invest the time/money.
Open source software has become widely used. Is Open source software frequently maintained, or do projects inhabit some form of zombie state?
Researchers have investigated various aspects of the life cycle of open source projects, including: maintenance activity, pull acceptance/merging or abandoned, and turnover of core developers; also, projects in niche ecosystems have been investigated.
The commits/pull requests/issues, of circa 1K project repos with lots of stars, is data that can be automatically extracted and analysed in bulk. What is missing from the analysis is the context around the creation, development and apparent abandonment of these projects.
Application areas and development tools (e.g., editor, database, gui framework, communications, scientific, engineering) tend to have a few widely used programs, which continue to be actively worked on. Some people enjoy creating programs/apps, and will start development in an area where there are existing widely used programs, purely for the enjoyment or to scratch an itch; rarely with the intent of long term maintenance, even when their project attracts many other developers.
I suspect that much of the existing research is simply measuring the background fizz of look-alike programs coming and going.
A more realistic model of the lifecycle of Open source projects requires human information; the intent of the core developers, e.g., whether the project is intended to be long-term, primarily supported by commercial interests, abandoned for a successor project, or whether events got in the way of the great things planned.
Clustering source code within functions
The question of how best to cluster source code into functions is a perennial debate that has been ongoing since functions were first created.
Beginner programmers are told that clustering code into functions is good, for a variety of reasons (none of the claims are backed up by experimental evidence). Structuring code based on clustering the implementation of a single feature is a common recommendation; this rationale can be applied at both the function/method and file/class level.
The idea of an optimal function length (measured in statements) continues to appeal to developers/researchers, but lacks supporting evidence (despite a cottage industry of research papers). The observation that most reported fault appear in short functions is a consequence of most of a program’s code appearing in short functions.
I have had to deal with code that has not been clustered into functions. When microcomputers took off, some businessmen taught themselves to code, wrote software for their line of work and started selling it. If the software was a success, more functionality was needed, and the businessman (never encountered a woman doing this) struggled to keep on top of things. A common theme was a few thousand lines of unstructured code in one function in a single file (keeping everything in one file is also a trait of highly focus developers).
Adding structural bureaucracy (e.g., functions and multiple files) reduced the effort needed to maintain and enhance the code.
The problem with ‘born flat’ source is that the code for unrelated functionality is often intermixed, and global variables are freely used to communicate state. I have seen the same problems in structured function code, but instances are nowhere near as pervasive.
When implementing the same program, do different developers create functions implementing essentially the same functionality?
I am aware of two datasets relating to this question: 1) when implementing the same small specification (average length program 46.3 lines), a surprising number of variants (6,301) are created, 2) an experiment that asked developers to reintroduce functions into ‘flattened’ code.
The experiment (Alexey Braver’s MSc thesis) took an existing Python program, ‘flattened’ it by inlining functions (parameters were replaced by the corresponding call arguments), and asked subjects to “… partition it into functions in order to achieve what you consider to be a good design.”
The 23 rows in the plot below show the start/end (green/brown delimited by blue lines) of each function created by the 23 subjects; red shows code not within a function, and right axis is percentage of each subjects’ code contained in functions. Blue line shows original (currently plotted incorrectly; patched original code+data):
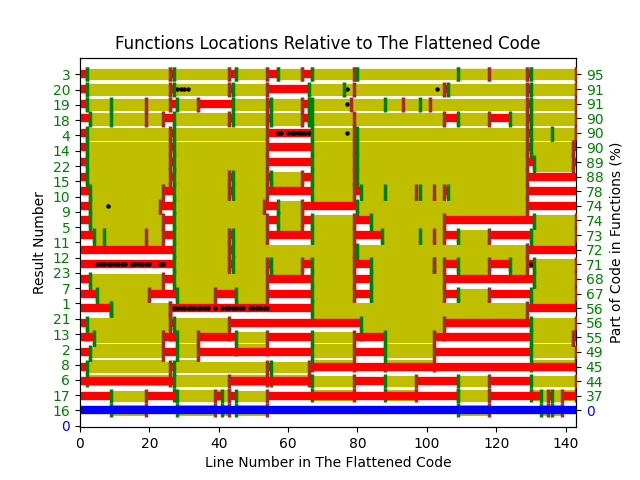
There are many possible reasons for the high level of agreement between subjects, including: 1) the particular example chosen, 2) the code was already well-structured, 3) subjects were explicitly asked to create functions, 4) the iterative process of discovering code that needs to be written did not occur, 5) no incentive to leave existing working code as-is.
Given that most source has a short and lonely existence, is too much time being spent bike-shedding function contents?
Given how often lower level design time happens at code implementation time, perhaps discussion of function contents ought to be viewed as more about thinking how things fit together and interact, than about each function in isolation.
Analyzing each function in isolation can create perverse incentives.
Printing press+widespread religious behavior: A theory
The book The Weirdest People in the World: How the West Became Psychologically Peculiar and Particularly Prosperous provides an explanation of the processes which weakened the existing social ties of family and tribe; however, the emergence of WEIRD people (Western, Educated, Industrialized, Rich and Democratic) required new social norms to spread and be accepted throughout society. A major technical innovation, in the form of the printing press, provided the means for mass communication of ideas and practices.
David High-Jones’ book Wyclif’s Dust: Western Cultures from the Printing Press to the Present describes the social consequences of what he calls book religion; a combination of deeply religious western societies and the ability of individuals to write and sell affordable books (made possible by the printing press). Religion+printing press created the conditions for what High-Jones calls a hothouse culture, a period from the 1600s to the end of the 1800s.
Around 1440 the printing press is invented and quickly spreads; around 5 million books were handwritten in the 1400s, about 80 million books were produced in the first 50 years of printing, and around a billion in the 1700s. During the 1500s the Protestant reformation happens; Protestant encouraged its followers to read the Bible, which creates a demand for printed Bibles and the need to be able to read (which increases literacy rates). In England, between 1480-1640, 40% of published books were religious.
The changes to society’s existing norms are wrought by cultural transmission, initially via middle class parents making use of edifying books to teach their children moral values and social skills, later Sunday schools took on this role, but also had to offer reading lessons to attract members. In the adult world, accepted norms were maintained by social enforcement. The impact on western societies was widespread because observant religious behavior was widespread.
The original intent, of those writing the religious books, was the creation of a god fearing society. In practice, a trust based society was created, where workers might be relied upon not to shirk their duties and businessmen to not renege on agreements.
In the beginning science, in the form of printed technical books, rarely made an appearance. In the 1700s the Enlightenment happens, and scientific books are discussed by small collections of disparate individuals. The industrial revolution happens, but the bulk of the demand is for trustworthy workers; technical and scientific know how remains a minority interest.
In Part I of the book, High-Jones weaves a reading and convincing narrative. Part II, 1900 to today, is a tale of the crumbling and breakdown of the social forces and incentives that creates the trust based society; while example are enumerated, no overarching theory is proposed (I skimmed this part).
Shopper estimates of the total value of items in their basket
Agile development processes break down the work that needs to be done into a collection of tasks (which may be called stories or some other name). A task, whose implementation time may be measured in hours or a few days, is itself composed of a collection of subtasks (which may in turn be composed of subsubtasks, and so on down).
When asked to estimate the time needed to implement a task, a developer may settle on a value by adding up estimates of the effort needed to implement the subtasks thought to be involved. If this process is performed in the mind of the developer (i.e., not by writing down a list of subtask estimates), the accuracy of the result may be affected by the characteristics of cognitive arithmetic.
Humans have two cognitive systems for processing quantities, the approximate number system (which has been found to be present in the brain of many creatures), and language. Researchers studying the approximate number system often ask subjects to estimate the number of dots in an image; I recently discovered studies of number processing that used language.
In a study by Benjamin Scheibehenne, 966 shoppers at the checkout counter in a grocery shop were asked to estimate the total value of the items in their shopping basket; a subset of 421 subjects were also asked to estimate the number of items in their basket (this subset were also asked if they used a shopping list). The actual price and number of items was obtained after checkout.
There are broad similarities between shopping basket estimation and estimating task implementation time, e.g., approximate idea of number of items and their cost. Does an analysis of the shopping data suggest ideas for patterns that might be present in software task estimate data?
The left plot below shows shopper estimated total item value against actual, with fitted regression line (red) and estimate==actual (grey); the right plot shows shopper estimated number of items in their basket against actual, with fitted regression line (red) and estimate==actual (grey) (code+data):
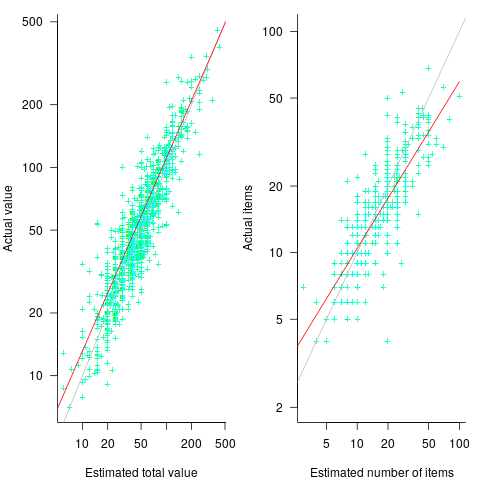
The model fitted to estimated total item value is: 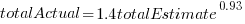 , which differs from software task estimates/actuals in always underestimating over the range measured; the exponent value,
, which differs from software task estimates/actuals in always underestimating over the range measured; the exponent value, 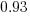 , is at the upper range of those seen for software task estimates.
, is at the upper range of those seen for software task estimates.
The model fitted to estimated number of items in the basket is: 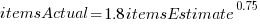 . This pattern, of underestimating small values and overestimating large values is seen in software task estimation, but the exponent of
. This pattern, of underestimating small values and overestimating large values is seen in software task estimation, but the exponent of 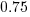 is much smaller.
is much smaller.
Including the estimated number of items in the shopping basket, 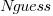 , in a model for total value produces a slightly better fitting model:
, in a model for total value produces a slightly better fitting model: 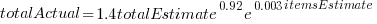 , which explains 83% of the variance in the data (use of a shopping list had a relatively small impact).
, which explains 83% of the variance in the data (use of a shopping list had a relatively small impact).
The accuracy of a software task implementation estimate based on estimating its subtasks dependent on identifying all the subtasks, or having a good enough idea of the number of subtasks. The shopping basket study found a pattern of inaccuracies in estimates of the number of recently collected items, which has been seen before. However, adding 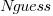 to the Shopping model only reduced the unexplained variance by a few percent.
to the Shopping model only reduced the unexplained variance by a few percent.
Would the impact of adding an estimate of the number of subtasks to models of software task estimates also only be a few percent? A question to add to the already long list of unknowns.
Like task estimates, round numbers were often given as estimate values; see code+data.
The same study also included a laboratory experiment, where subjects saw a sequence of 24 numbers, presented one at a time for 0.5 seconds each. At the end of the sequence, subjects were asked to type in their best estimate of the sum of the numbers seen (other studies asked subjects to type in the mean). Each subject saw 75 sequences, with feedback on the mean accuracy of their responses given after every 10 sequences. The numbers were described as the prices of items in a shopping basket. The values were drawn from a distribution that was either uniform, positively skewed, negatively skewed, unimodal, or bimodal. The sequential order of values was either increasing, decreasing, U-shaped, or inversely U-shaped.
Fitting a regression model to the lab data finds that the distribution used had very little impact on performance, and the sequence order had a small impact; see code+data.
Recent Comments