Archive
Is the code reuse problem now solved?
Writing a program to solve a problem involves breaking the problem down into subcomponents that have a known coding solution, and connecting the input/output of these subcomponents into sequences that produced the desired behavior.
When computers first became available, developers had to write every subcomponent. It was soon noticed that new programs contained some functionality that was identical to functionality present in previously written programs, and software libraries were created to reduce development cost/time through reuse of existing code. Developers have being sharing code since the very start of computing.
To be commercially viable, computer manufacturers discovered that they not only had to provide vendor specific libraries, they also had to support general purpose functionality, e.g., sorting and maths libraries.
The Internet significantly reduced the cost of finding and distributing software, enabling an explosion in the quality and quantity of publicly available source code. It became possible to write major subcomponents by gluing together third-party libraries and packages (subject to licensing issues).
Diversity of the ecosystems in which libraries/packages have to function means that developers working in different environments have to apply different glue. Computing diversity increases costs.
A lot of effort was invested in trying to increase software reuse in a very diverse world.
In the 1990 there was a dramatic reduction in diversity, caused by a dramatic reduction in the number of distinct cpus, operating systems and compilers. However, commercial and personal interests continue to drive the creation of new cpus, operating systems, languages and frameworks.
The reduction in diversity has made it cheaper to make libraries/packages more widely available, and reduced the variety of glue coding patterns. However, while glue code contains many common usage patterns, they tend not to be sufficiently substantial or distinct enough for a cost-effective reuse solution to be readily apparent.
The information available on developer question/answer sites, such as Stackoverflow, provides one form of reuse sharing for glue code.
The huge amounts of source code containing shared usage patterns are great training input for large languages models, and widespread developer interest in these patterns means that the responses from these trained models is of immediate practical use for many developers.
LLMs appear to be the long sought cost-effective solution to the technical problem of code reuse; it’s too early to say what impact licensing issues will have on widespread adoption.
One consequence of widespread LLM usage is a slowing of the adoption of new packages, because LLMs will not know anything about them. LLMs are also the death knell for fashionable new languages, which is a very good thing.
Distribution of binary operator results
As numeric values percolate through a program they appear as the operands of arithmetic operators whose results are new values. What is the distribution of binary operator result values, for a given distribution of operand values?
If we start with independent random values drawn from a uniform distribution, 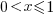 , then:
, then:
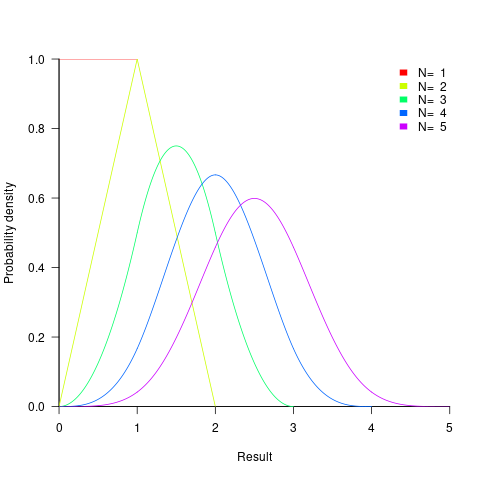
- the distribution of the result of adding two such values has a triangle distribution, and the result distribution from adding
 such values is known as the Irwin-Hall distribution (a polynomial whose highest power is
such values is known as the Irwin-Hall distribution (a polynomial whose highest power is 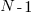 ). The following plot shows the probability density of the result of adding 1, 2, 3, 4, and 5 such values (code+data):
). The following plot shows the probability density of the result of adding 1, 2, 3, 4, and 5 such values (code+data):
- the distribution of the result of multiplying two such values has a logarithmic distribution, and when multiplying
 such values the probability of the result being
such values the probability of the result being  is:
is: 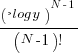 .
.
If the operand values have a lognormal distribution, then the result also has a lognormal distribution. It is sometimes possible to find a closed form expression for operand values having other distributions.
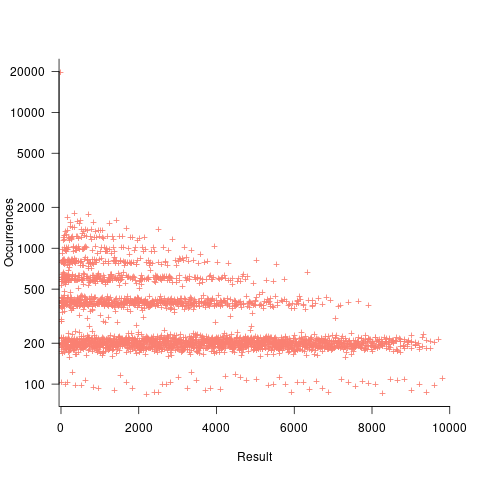
If both operands take integer values, including zero, some result values are more likely to occur than others; for instance, there are six unique factor pairs of positive integers that when multiplied return sixty, and of course prime numbers only have one factor-pair. The following plot was created by randomly generating one million pairs of values between 0 and 100 from a uniform distribution, multiplying each pair, and counting the occurrences of each result value (code+data):
- the probability of the result of dividing two such values being
 is: 0.5 when
is: 0.5 when 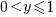 , and
, and 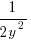 when
when 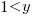 .
.
The ratio of two distributions is known as a ratio distribution. Given the prevalence of Normal distributions, their ratio distribution is of particular interest, it is a Cauchy distribution:
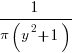 ,
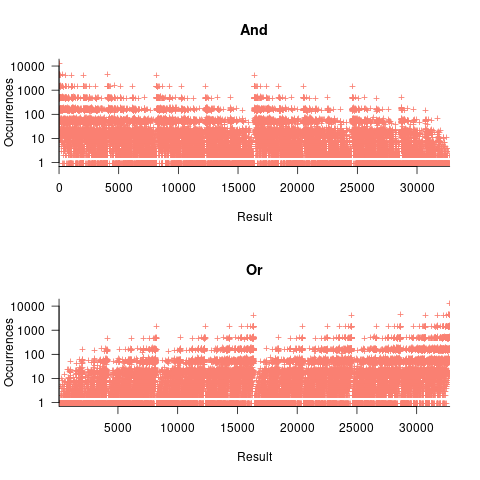
, - the result distribution of the bitwise and/or operators is not continuous. The following plots were created by randomly generating one million pairs of values between 0 and 32,767 from a uniform distribution, performing a bitwise AND or OR, and counting the occurrences of each value (code+data):
- the result distribution of the bitwise exclusive-or operator is uniform, when the distribution of its two operands is uniform.
The mean value of the Irwin-Hall distribution is 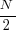 and its standard deviation is
and its standard deviation is 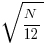 . As
. As 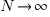 , the Irwin-Hall distribution converges to the Normal distribution; the difference between the distributions is approximately:
, the Irwin-Hall distribution converges to the Normal distribution; the difference between the distributions is approximately: 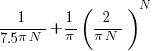 .
.
The sum of two or more independent random variables is the convolution of their individual distributions,
The banding around intervals of 100 is the result of values having multiple factor pairs. The approximately 20,000 zero results are from two sets of 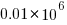 multiplications where one operand is zero,
multiplications where one operand is zero,
The vertical comb structure is driven by power-of-two bits being set/or not. For bitwise-and the analysis is based on the probability of corresponding bits in both operands being set, e.g., there is a 50% chance of any bit being set when randomly selecting a numeric value, and for bitwise-and there is a 25% chance that both operands will have corresponding bits set; numeric values with a single-bit set are the most likely, with two bits set the next most likely, and so on. For bitwise-or the analysis is based on corresponding operand bits not being set,
The general pattern is that sequences of addition produce a centralizing value, sequences of multiplies a very skewed distribution, and bitwise operations combed patterns with power-of-two boundaries.
This analysis is of sequences of the same operator, which have known closed-form solutions. In practice, sequences will involve different operators. Simulation is probably the most effective way of finding the result distributions.
How many operations is a value likely to appear as an operand? Apart from loop counters, I suspect very few. However, I am not aware of any data that tracked this information (Daikon is one tool that might be used to obtain this information), and then there is the perennial problem of knowing the input distribution.
How much productive work does a developer do?
Measuring develop productivity is a nightmare issue that I do my best to avoid.
Study after study has found that workers organise their work to suit themselves. Why should software developers be any different?
Studies of worker performance invariably find that the rate of work is higher when workers are being watched by researchers/managers; this behavior is known as the Hawthorne effect. These studies invariably involve some form of production line work involving repetitive activities. Time is a performance metric that is easy to measure for repetitive activities, and directly relatable to management interests.
A study by Bernstein found that production line workers slowed down when observed by management. On the production line studied, it was not possible to get the work done in the allotted time using the management prescribed techniques, so workers found more efficient techniques that were used when management were not watching.
I have worked on projects where senior management decreed that development was to be done according to some latest project management technique. Developers quickly found that the decreed technique was preventing work being completed on time, so ignored it while keeping up a facade to keep management happy (who appeared to be well aware of what was going on). Other developers have told me of similar experiences.
Studies of software developer performance often implicitly assume that whatever the workers (i.e., developers) say must be so; there is no thought given to the possibility that the workers are promoting work processes that suits their interests and not managements.
Just like workers in other industries, software developers can be lazy, lack interest in doing a good job, unprofessional, a slacker, etc.
Hard-working, diligent developers can be just as likely as the slackers, to organise work to suit themselves. A good example of this is adding product features that the developer wants to add, rather than features that the customer wants to use, or working on features/performance that exceed the original requirements (known as gold plating in other industries).
Developers will lobby for projects to use the latest language/package/GUI/tools in their work. While issues around customer/employer cost/benefit might be cited as a consideration, evidence, in the form of a cost/benefit analysis, is not usually given.
Like most people, developers want others to have a good opinion of them. As writers, of code, developers can attach a lot of weight to how its quality will be perceived by other developer. One consequence of this is a willingness to regularly spend time polishing good-enough code. An economic cost/benefit of refactoring is rarely a consideration.
The first step of finding out if developers are doing productive work is finding out what they are doing, or even better, planning in some detail what they should be doing.
Developers are not alone in disliking having their activities constrained by detailed plans. Detailed plans imply some form of estimates, and people really hate making estimates.
My view of the rationale for estimating in story points (i.e., monopoly money) is that they relieve the major developer pushback on estimating, while allowing management to continue to create short-term (e.g., two weeks) plans. The assumption made is that the existence of detailed plans reduces worker wiggle-room for engaging in self-interest work.
Percolation of the impact of coding mistakes through a program
Programs containing serious coding mistakes can sometimes work surprisingly well. Experienced developers invariably have a story to tell about a program in production use that contained a coding mistake so bad, that it should have prevented the program producing any reliably output. My story relates to a Z80 cpu emulator I had written, which was successfully booting/running CP/M and several applications. One application was sometimes behaving erratically. I eventually traced the problem to the implementation of one of the add instructions (there are 13 special cases), which had been cut/pasted from the implementation of the corresponding subtract instruction, except that I had forgotten to change the result calculation from using a subtract to using an add, i.e., the instruction was performing a subtract, not an add. I was flabbergasted that so much emulated code appeared to be working in the presence of what to me was a crippling coding mistake.
There have been a handful of studies investigating the ability of programs containing coding mistakes to function correctly, or at least well enough to be usable.
- The earliest paper I have found is from 2005; Rinard, Cadar and Nguyen changed the termination condition of 326
for-loopsin the Pine email client, with<becoming<=, and>becoming>=. While the resulting program exhibited obvious anomalies, the researchers were able to use it to send and receive email, - a study by Danglot, Preux, Baudry and Monperrus investigated the propagation of single perturbations in 10 short Java programs (42 to 568 LOC, perturbed by adding/subtracting 1 from an expression somewhere in the code). The plot below shows the likelihood that a perturbation at some point in the code will have no impact on the output; code+data,

- a study by Cho of the impact of soft errors (i.e., radiation induced bit-flips) found that over 80% of bit-flips had no detectable impact on program behavior.
This week I attended the 63rd CREST Open Workshop; the topic was genetic improvement of software, i.e., GI randomly combines members of a population of programs, only keeping the children that pass some fitness test, rinses and repeats until one or more programs reach some acceptance threshold.
The GI community recently discovered that program output is often unaffected by a small perturbation to program execution, e.g., randomly adding one to the result of a binary operation.
A study by Langdon, Al-Subaihin and Clark tracked the effect of perturbations in the evaluation of an expression tree. The expression trees were created using genetic programming, with the fitness function being the difference between the value obtained by evaluating the expression tree and a sixth order polynomial. The binary operators in the expression tree were multiply and addition, with the leaf node value, x, taking a value between -0.97789 and 0.979541; the trees were a lot deeper than the one below, containing between 8.9k and 863k nodes/leafs, with tree depth varying from 121 to 5,103.
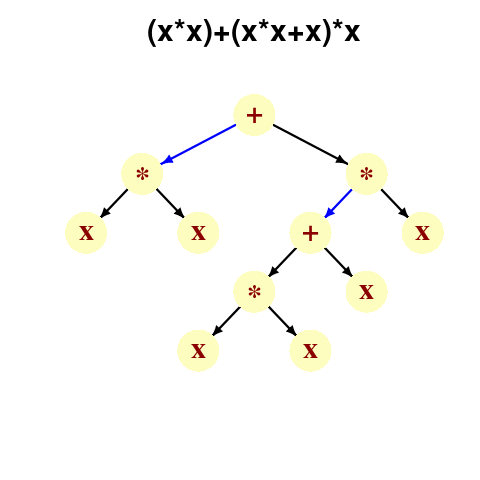
During the evaluation of an expression tree the result of one of the multiply/add operations was perturbed by adding one to its value. The subsequent evaluation of the remainder of the expression tree was tracked, comparing original/perturbed calculated values until either the root node was reached (and the final result was different), or the original/perturbed subtree result values synchronized, i.e., became the same. The distance, in nodes, between perturbation and value synchronization was recorded.
In all, ten expression trees were created, and each node in every tree was perturbed once per run; there were 10 runs using 10 different values of x.
The plot below shows results from two expression trees (different colors). Each point is the distance before original/perturbed values synchronised (for those cases where this happened) against the number of runs having this distance (for the same tree; code+data, and thanks to Bill for explaining things):
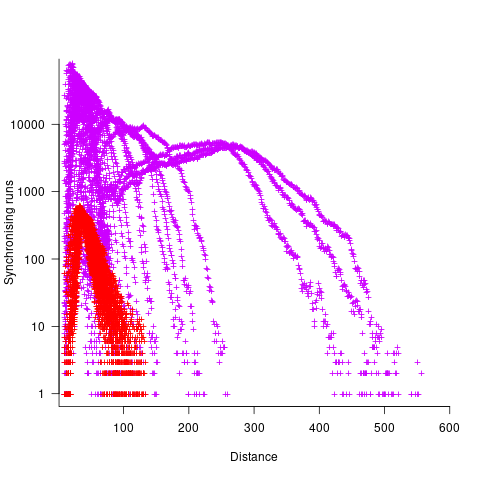
For the larger tree, there is a distinct pattern for each of the ten input values, x. This shows that synchronisation distance can be affected by the input value (which is to be expected). Perhaps this pattern is not present in the smaller tree, or the points are too close together to see it.
The opportunities available to a perturbation for travelling some distance depends on the size and characteristics of the expression tree, with a large thin tree providing more opportunities for longer distance travel than a large bushy tree.
It will take some well thought through experiments to unpick the contributions made by the tree characteristics, problem characteristics, and the prevalence of binary operators unlikely to be affected by small changes to their operand value, e.g., there is roughly a 50% chance that a relational comparison will be unaffected by a small change to one of its operands.
If you know of any other studies investigating coding mistake percolation, please let me know.
Analysis of when refactoring becomes cost-effective
In a cost/benefit analysis of deciding when to refactor code, which variables are needed to calculate a good enough result?
This analysis compares the excess time-code of future work against the time-cost of refactoring the code. Refactoring is cost-effective when the reduction in future work time is less than the time spent refactoring. The analysis finds a relationship between work/refactoring time-costs and number of future coding sessions.
Linear, or supra-linear case
Let’s assume that the time needed to write new code grows at a linear, or supra-linear rate, as the amount of code increases (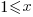 ):
):
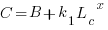
where: 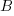 is the base time for writing new code on a freshly refactored code base,
is the base time for writing new code on a freshly refactored code base, 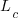 is the number of lines of code that have been written since the last refactoring, and
is the number of lines of code that have been written since the last refactoring, and 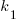 and
and  are constants to be decided.
are constants to be decided.
The total time spent writing code over  sessions is:
sessions is:
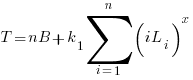
If the same number of new lines is added in every coding session, 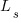 , and
, and  is an integer constant, then the sum has a known closed form, e.g.:
is an integer constant, then the sum has a known closed form, e.g.:
x=1, 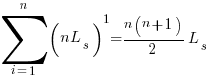 ; x=2,
; x=2, 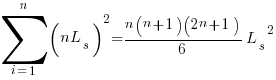
Let’s assume that the time taken to refactor the code written after  sessions is:
sessions is:
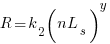
where: 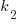 and
and  are constants to be decided.
are constants to be decided.
The reason for refactoring is to reduce the time-cost of subsequent work; if there are no subsequent coding sessions, there is no economic reason to refactor the code. If we assume that after refactoring, the time taken to write new code is reduced to the base cost, 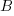 , and that we believe that coding will continue at the same rate for at least another
, and that we believe that coding will continue at the same rate for at least another  sessions, then refactoring existing code after
sessions, then refactoring existing code after  sessions is cost-effective when:
sessions is cost-effective when:
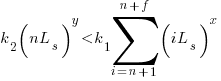
assuming that  is much smaller than
is much smaller than  , setting
, setting 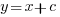 , and rearranging we get:
, and rearranging we get:
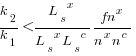
after rearranging we obtain a lower limit on the number of future coding sessions,  , that must be completed for refactoring to be cost-effective after session
, that must be completed for refactoring to be cost-effective after session  ::
::
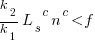
It is expected that 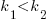 ; the contribution of code size, at the end of every session, in the calculation of
; the contribution of code size, at the end of every session, in the calculation of  and
and  is equal (i.e.,
is equal (i.e., 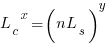 ), and the overhead of adding new code is very unlikely to be less than refactoring all the newly written code.
), and the overhead of adding new code is very unlikely to be less than refactoring all the newly written code.
With 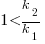 ,
,  must be close to zero; otherwise, the likely relatively large value of
must be close to zero; otherwise, the likely relatively large value of 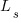 (e.g., 100+) would produce surprisingly high values of
(e.g., 100+) would produce surprisingly high values of  .
.
Sublinear case
What if the time overhead of writing new code grows at a sublinear rate, as the amount of code increases?
Various attributes have been found to strongly correlate with the 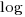 of lines of code. In this case, the expressions for
of lines of code. In this case, the expressions for  and
and 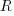 become:
become:
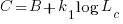
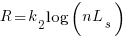
and the cost/benefit relationship becomes:

applying Stirling’s approximation and simplifying (see Exact equations for sums at end of post for details) we get:
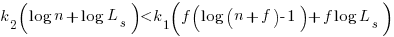
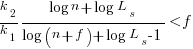
applying the series expansion (for 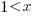 ):
): 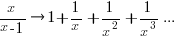 , we get
, we get
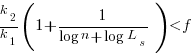
Discussion
What does this analysis of the cost/benefit relationship show that was not obvious (i.e., the relationship 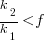 is obviously true)?
is obviously true)?
What the analysis shows is that when real-world values are plugged into the full equations, all but two factors have a relatively small impact on the result.
A factor not included in the analysis is that source code has a half-life (i.e., code is deleted during development), and the amount of code existing after  sessions is likely to be less than the
sessions is likely to be less than the 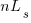 used in the analysis (see Agile analysis).
used in the analysis (see Agile analysis).
As a project nears completion, the likelihood of there being  more coding sessions decreases; there is also the every present possibility that the project is shutdown.
more coding sessions decreases; there is also the every present possibility that the project is shutdown.
The values of 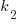 and
and 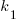 encode information on the skill of the developer, the difficulty of writing code in the application domain, and other factors.
encode information on the skill of the developer, the difficulty of writing code in the application domain, and other factors.
Exact equations for sums
The equations for the exact sums, for 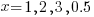 , are:
, are:
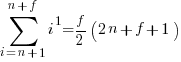
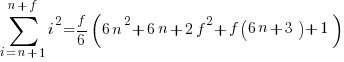
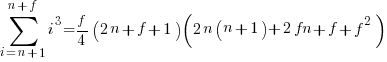
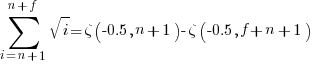 , where
, where 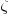 is the Hurwitz zeta function.
is the Hurwitz zeta function.
Sum of a log series: 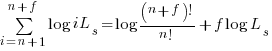
using Stirling’s approximation we get
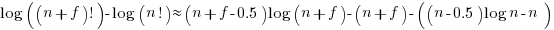
simplifying
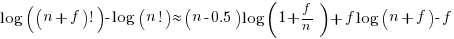
and assuming that  is much smaller than
is much smaller than  gives
gives
My new laptop
I have been using the same MacBook Pro for almost nine years; yes, I’m a sporadic user of laptops, much preferring to work on a decent desktop system. I’ve had zero hardware problems, and have often been able to install programs (often by compiling from source) from the weird and wonderful ecosystems I frequent. Performance does seem to have gotten slower with every OS upgrade (it ‘only’ has 8G of memory). I’m very happy with the eight years of software support provided by Apple; while I’m usually happy to stay with older versions of software, package vendors eventually stop supporting them, ‘forcing’ me to upgrade.
My decision about which laptop to buy next is software driven: Over the next, say, five years which of Apple’s OS X or Linux is most likely to best support the software ecosystems containing the kind of programs I am going to want to run (given a Windows laptop, my first action would be to install the Linux subsystem)?
Diehard Mac fans complain that Apple has lost its way, with regard to Mac upgrades; this does not bother me too much. I am more concerned with the increasing number of features that smack of a walled garden approach to software that is permitted to run on Apple hardware.
My need for a new laptop has not been urgent, and for the last 18-months I have been keeping an eye out for the hardware options that are available for a laptop running Linux.
The most obvious option is buying a Windows laptop from a major supplier, and doing a clean Linux installation; yes, some larger suppliers offer laptops with Linux preinstalled.
About a year ago, I saw a review for the StarBook, which is essentially a hackers’ 14″ laptop built by a bunch of hackers for a living. The hardware specs looked good, with plenty of upgrade options, and choice of preinstalled Linux distribution. While I continue to build desktop systems, I don’t plan to get involved with laptop hardware; however, it’s good to see that Starlab Systems publish complete disassembly instructions.
Around a month ago I finally had had enough with my sluggish MacBook and ordered a StarBook (32G memory, 960G SSD). I initially specified Ubuntu as the installed distribution, but on learning that some Ubuntu tools now produced promotional messages, I switched to Linux Mint.
The StarBook arrived a couple of weeks ago, and is certainly a lot faster than my 2013 MacBook (Geekbench cpu results). There has been the usual period of installing packages and configuring the system (I have yet to spend the time need to figure out how to get Cinnamon (the desktop environment) to save/restore the terminal windows across shutdown (the one OSX feature I miss).
All being well, I may be writing again about my new laptop in 2032.
My MacBook, StarBook and Samsung 32-inch curved monitor. While the laptops have very similar length/width, the screen size of the StarBook is 1-inch greater.
Modular Reasoning, Knowledge and Language systems
The spectrum of models of the human mind run from it being a general purpose computer to it being a collection of integrated specialist modules (each performing one function, e.g., speech or language). The Modularity of mind hypothesis offers a halfway house.
ChatGPT sits at the general purpose computer end of the spectrum; there is a single ‘processor’ that accepts a particular kind of input and produces a particular kind of output.
While predict-the-next-token systems like ChatGTP have proven to be good at analysing and constructing sentences, they are often unable to carry out the actions described by these sentences; for instance, they are capable of describing mathematical operations that they are incapable of performing (unless the answer happens to be in their training).
A Modular Reasoning, Knowledge and Language system (MRKL; the suggested pronunciation is miracle), is, as the name suggests, a system built from specialist modules. In this approach, a large language model (LLM), such as ChatGTP, is the language processing module.
In a MRKL system, the input is processed (by an LLM) to figure out which specialist modules have to be queried to obtain the information needed to answer the question, the appropriate text (generated by an LLM) is fed as input to the corresponding modules, and the module outputs are collected and fed to an LLM to generate an answer to the question.
A user question may involve querying multiple modules in some sequence. For instance, the question “What is the average age of the last five British Prime ministers?” might involve querying Google/Alexa answers to obtain a list of previous Prime ministers, followed by extracting individual ages from Wikipedia, followed by querying a maths module to obtain the average of the five ages obtained.
The extent to which an application using an LLM might be said to be a MRKL system is a matter of degree. The following shell script is unlikely to qualify:
curl https://api.openai.com/v1/completions \
-H 'Content-Type: application/json' \
-H 'Authorization: Bearer '{$OPENAI_API_KEY} \
-d '{
"model": "text-davinci-003",
"prompt": "Say I found The Shape of Code to be an interesting blog",
"temperature": 0
}' |
The OpenAI API focuses on how to drive their various language models, along with lots of examples. There is no API offering a higher level abstraction or functionality.
An API designed for building MRKL systems, that is starting to gain traction, is langchain; a collection of Python packages, with JavaScript libraries playing catchup.
langchain Module categories include: LLM interaction (e.g., specifying which LLM to use, API keys, and changing default values), document loaders (e.g., readers for pdf, HTML, Gitbook, and Microsoft Word), Agents (these use an LLM to process the input text to find out what actions need to be performed, and to create the input actions that the selected modules need to perform), Memory (store information from previous interactions; other modules can be stateless), and Chat (handle the mechanics of holding a conversation).
What does langchain offer that is making it attractive to a growing number of developers?
- Making use of an LLM within an application will involve some subset of the functionality provided by langchain. The advantage of using langchain is that it provides a framework, MRKL, along with a (sometimes skeleton) existing implementation,
- first mover advantage for an Open source implementation has enabled langchain to attract a growing number of active contributors; it also helps that the core developers have been making regular updates (almost daily), and half-decent documentation is available.
Given the current volume of discussion around LLMs, why has there been so little written about MRKL systems?
Building a MRKL system requires coding ability, and developers are a small percentage of those contributing to the discussion avalanche.
Building a MRML system takes a lot of time and work. Being able to break down a question into subcomponents that can be answered by the available modules, and sequencing them appropriately is a non-trivial problem.
Once Apps solving real-world problems start becoming widely used, and the novelty of generic chat systems wears off, the discussion will switch to more grounded issues.
2023 in the programming language standards’ world
Two weeks ago I was on a virtual meeting of IST/5, the committee responsible for programming language standards in the UK. IST/5 has a new chairman, Guy Davidson, whose efficiency is very unstandard’s like.
It’s been 18 months since I last reported on the programming language standards’ world, what has been going on?
2023 is going to be a bumper year for the publication of revised Standards of long-established programming language: COBOL, Fortran, C, and C++ (a revised Standard for Ada was published last year).
Yes, COBOL; a new COBOL Standard was published in January. Reports of its death were premature, e.g., my 2014 post suggesting that the latest version would be the last version of the Standard, and the closing of PL22.4, the US Cobol group, in 2017. There has even been progress on the COBOL front end for gcc, which now supports COBOL 85.
The size of the COBOL Standard has leapt from 955 to 1,229 pages (around new 200 pages in the normative text, 100 in the annexes). Comparing the 2014/2023 documents, I could not see any major additions, just lots of small changes spread throughout the document.
Every Standard has a project editor, the person tasked with creating a document that reflects the wishes/votes of its committee; the project editor sends the agreed upon document to ISO to be published as the official ISO Standard. The ISO editors would invariably request that the project editor make tiresome organizational changes to the document, and then add a front page and ISO copyright notice; from time to time an ISO editor took it upon themselves to reformat a document, sometimes completely mangling its contents. The latest diktat from ISO requires that submitted documents use the Cambria font. Why Cambria? What else other than it is the font used by the Microsoft Word template promoted by ISO as the standard format for Standard’s documents.
All project editors have stories to tell about shepherding their document through the ISO editing process. With three Standards (COBOL lives in a disjoint ecosystem) up for publication this year, ISO editorial issues have become a widespread topic of discussion in the bubble that is language standards.
Traditionally, anybody wanting to be actively involved with a language standard in the UK had to find the contact details of the convenor of the corresponding language panel, and then ask to be added to the panel mailing list. My, and others, understanding was that provided the person was a UK citizen or worked for a UK domiciled company, their application could not be turned down (not that people were/are banging on the door to join). BSI have slowly been computerizing everything, and, as of a few years ago, people can apply to join a panel via a web page; panel members are emailed the CV of applicants and asked if “… applicant’s knowledge would be beneficial to the work programme and panel…”. In the US, people pay an annual fee for membership of a language committee ($1,340/$2,275). Nobody seems to have asked whether the criteria for being accepted as a panel member has changed. Given that BSI had recently rejected somebodies application to join the C++ panel, the C++ panel convenor accepted the action to find out if the rules have changed.
In December, BSI emailed language panel members asking them to confirm that they were actively participating. One outcome of this review of active panel membership was the disbanding of panels with ‘few’ active members (‘few’ might be one or two, IST/5 members were not sure). The panels that I know to have survived this cull are: Fortran, C, Ada, and C++. I did not receive any email relating to two panels that I thought I was a member of; one or more panel convenors may be appealing their panel being culled.
Some language panels have been moribund for years, being little more than bullet points on the IST/5 agenda (those involved having retired or otherwise moved on).
Small team estimating in story points; a project dataset
Just before the end of last year a regular reader, Mr A., emailed to ask if I would be interested in analysing the software project data for the company he worked for. The wishing to be anonymous company sold physical products, and bespoke software that supported the business was written by a team of three.
Two factors made this dataset interesting, 1) it was for a small team, 2) story points were used for estimating tasks and actual time was recorded (I had not seen such data before).
There are probably hundreds of thousands of small software teams working in companies whose main line of business is far removed from software (a significant percentage of developers work within a small team supporting the activities of non-software companies; I cannot find the bls page listing developer employment across industry codes). These small teams are rarely studied. Software engineering research usually focuses on the practices of software based companies, or large software development projects, i.e., groups likely to be easily visible to external researchers.
To be widely applicable, evidence-based software engineering has to be of practical use to small development teams, not just large development groups.
The wide variety of opinions on the accuracy of story point estimates are unsupported by data; at least I have not yet been able to find any. Here was an opportunity to analyse story point estimates against actual hours.
The reason for analysing task implementation data is to help those involved understand what is going on, with the intent of improving processes. A small team presents two major challenges:
- relatively high levels of variability in the data. When there are only a few people working on a project, the impact of individual events can have a dramatic impact on project metrics, e.g., somebody going on holiday results in a big drop in work performed. Statistical analysis looks for general patterns in data, and small sample sizes have a higher variance than large sample sizes. With a large team, the impact of individual events tends to be smoothed out by the activities of many other events,
- the project lead of a small team is likely to have a good understanding of what is going on. Mr A. was always able to give me detailed explanations behind the patterns I found in the data. There is a lot more going on in a large team, and the team lead is unlikely to have a detailed understanding of everything.
The dataset contained some of the usual patterns found in other datasets (code+data):
- Round numbers. Actual task time finishing on 15/10/30/20 minute boundaries. With stories estimated at between one and five story points, there was little scope for round number use here.
- Consistent under/over estimation. A small sample size limited the chances of seeing both under and over estimation, and only under estimation was seen.
- Estimation accuracy. The factor of two/four accuracy pattern seen is close to that seen in data from other companies.
What did I learn from the analysis of this dataset?
I was pleased to see that the multiplication factors around estimation accuracy were similar to those seen with time-based estimates. I had no feel for how estimation accuracy might compare. We will have to wait and see whether the same pattern is found in other projects using story point estimates.
The analysis conversation for other project datasets had involved exchange of emails. Updating a Markdown formatted project analysis file has proved to be a more usable approach for the conversation between me and the domain expert. I used Visual Studio Code to edit this file and generate a pdf.
I asked Mr A. what would he thought was the most useful part of the analysis, for him.
Mr A. “The most useful part of the analysis? I think it was great to get an outsider’s perspective on the data.”
I hope that this dataset is the first of many from small team projects. With enough experience, it ought to be possible to create a template spreadsheet/markdown file that is generally usable for non-experts.
Human reasoning is generally not logic based
From around 350 BC until the 1960s, the students were taught that people reasoned using logic, and teachers believed this to be true. In the 1960s psychologists started running experiments that asked subjects to solve reasoning problems, the results showed that people often failed to give the answers dictated by logic.
Some recurring patterns were present in the answers given, and small changes in the wording of the question asked were found to produce different answer patterns. Very few researchers were willing to give up the idea that subjects were reasoning using logic, there must be another explanation, e.g., subjects must be interpreting the experimental questions asked in a way that differed from that assumed by the researchers. The social context of reasoning was one of the early drivers of evolutionary psychology; reasoning must provide some survival benefit by solving problems that regularly occur in natural human environments.
After a myriad of detailed theories did little more than predict small subsets of subject responses, mainstream reasoning research finally gave up the belief that logic is the default technique used by people to solve reasoning problems. Theories of reasoning behavior are now based around people estimating probabilities and picking the answer with the highest probability; this approach does a much better job of predicting common patterns in subject answers.
Experimental studies of reasoning often use psychology undergraduates as subjects (the historical norm, with Mechanical Turk workers becoming more common). While researchers may be concerned about how well undergraduate behavior mimics the general population, my concern is the extent to which these results apply to software developers. Is a necessary condition for being a professional software developer that a person, by default, uses logic to solve reasoning problems?
Of course, software developers claim that their reasoning is logic based, but then so do people in the general population (or at least the non-developers I interact with do). The dual-process theory of reasoning contains two reasoning systems, one unconscious/intuitive and the second a conscious/deliberate system; it has been said that the purpose of the second system is to come up with reasons to justify the answers produced by the first system.
Until reasoning experiments are run with professional developer subjects, we won’t know the extent to which existing results in reasoning research apply to this specialist subset of the population.
The Wason selection task is to studies of reasoning, like the fruit fly is to studies of genetics. What pattern of behavior do you show on this task (code)?
The plot below shows a set of four cards, of which you can see only the exposed face but not the hidden back. On each card, there is a number on one side and a letter on the other.
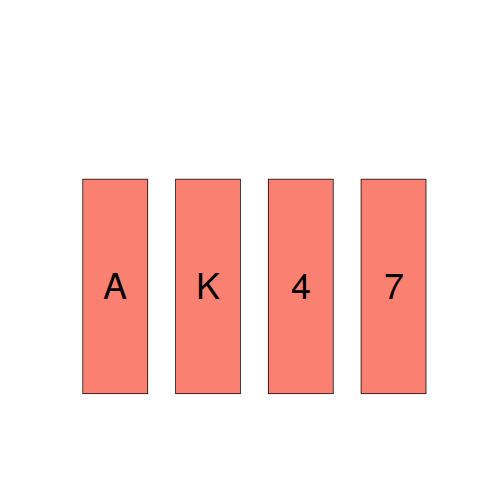
- Given the statement: “If there is a vowel on one side, then there is an even number on the other side.”
Your task is to decide, which, if any, of these four cards must be turned over to decide whether this statement is true. - Specify the cards you would turn over. Don’t turn unnecessary cards.
————————————
Most people correct specify that the card showing a vowel must be turned over to verify that an even number appears on the other side. A common mistake is to specify that the card showing an even number also has to be turned over. However, there is no requirement on the letter appearing on the other side of a card showing an even number. A second necessary condition involves a negative test (something that developers are known to overlook); for the statement to hold, a vowel must not appear on the other side of the card showing an odd number, this is the second card that must be turned over.
Recent Comments