Archive
A safety-critical certification of the Linux kernel
This week there was an announcement on the system-safety mailing list that the Red Hat In-Vehicle Operating System (a version of the Linux kernel, plus a few subsystems) had been certified as being “… capable for use in ASIL B applications, …”. The Automotive Safety Integrity Levels (ASIL A is the lowest level, with D the highest; an example of ASIL B is controlling brake lights) are defined by ISO 26262, an international standard for functional safety of electrical and/or electronic systems installed in production road vehicles.
Given all I had heard about the problems that needed to be solved to get a safety certification for something as large and complicated as the Linux kernel, I wanted to know more about how Red Hat had achieved this certification.
The traditional, idealised, approach to certifying software is to check that all requirements are documented and traceable to the design, source code, tests, and test results. This information can be used to ensure that every requirement is implemented and produces the intended behavior, and that no undocumented functionality has been implemented.
When this approach is not practical (because of onerous time/cost), a potential get out of jail card is to use a Rigorous Development Process. Certification friendly development processes appear to revolve around lots of bureaucracy and following established buzzword techniques. The only development processes that have sometimes produced very reliable software all involve spending lots of time/money.
The major problems with certifying Linux are the apparent lack of specification/requirements documents, and a development process that does not claim to be rigorous.
The Red Hat approach is to treat the Linux man pages as the specification, extract the requirements from these pages, and then write the appropriate tests. Traceability looks like it is currently on the to-do list.
I have spent a lot of time working to understand specifications and their requirements; first with the C Standard and then with the Microsoft Server Protocols. This is the first time I have encountered man pages being used in a formal setting (sometimes they are used as one of the inputs to a reimplementation of a library).
Very little Open source software has a written specification in the traditional sense of a document cited in a contract that the vendor agrees to implement. Manuals, READMEs and help pages are not written in the formal style of a specification. A common refrain is that the source code is the specification. However, source is a specification of what the program does, it is not a specification of what the program is supposed to do.
The very nature of the Agile development process demands that there not be a complete specification. It’s possible that user stories could be treated as requirements.
There is an ISO Standard with Linux in its title: the Linux Base Standard. The goal of this Standard “… is to develop and promote a set of open standards that will increase compatibility among Linux distributions and enable software applications to run on any compliant system …”, i.e., it is not a specification of an OS kernel.
POSIX is a specification of the behavior of an OS (kernel functionality is specified by POSIX.1, .2 is shell and utilities, plus other .x documents). It’s many years since I tracked POSIX/Linux compliance, which was best described as “highly compatible”. Both Grok3 and ChatGPT o4 agree that “highly compatible” is still true, and list some known incompatibilities.
While they are not written in the form of a specification, the Linux man pages do have a consistent structure and are intended to be up-to-date. A person with a background of working with Linux kernels could probably extract meaningful requirements.
How many requirements are needed to cover the behavior of the Linux kernel?
On my computer running a 6.8.0-51 kernel, the /usr/include/linux directory contains 587 header files. Based on an analysis from 20 years ago (table 1897.1), most of these headers only declare macros and types (e.g., memory layout), not function declarations. The total number of function declarations in these headers is probably in the low thousands. POSIX (2008 version) defines 1,177 functions, but the number of system calls is probably around 300-400. Android implements 821 of these functions, of which 343 are system call related.
Let’s assume 2,000 functions. Some of these functions have an argument that specifies one or more optional values, each specifying a different sub-behavior. How many different sub-behaviors are there? If we assume that each kind of behavior is specified using a C macro, then Table 1897.1 suggests there might be around 10k C macros defined in these headers.
With positive/negative tests for each case, in round numbers we get (ignoring explicit testing of the values of struct members): 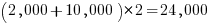 test files.
test files.
This calculation does not take into account combinations of options. I’m assuming that each test file will loop through various combinations of its kind of sub-behavior.
The 1990 C compiler validation suite contained around 1k tests. Thirty-five years later, 24k test files for a large OS feels low, but then combination testing should multiply the number of actual tests by at least an order of magnitude.
What is this hand-wavy analysis missing?
I suspect that the kernel is built with most of the optional functionality conditionally compiled out. This could significantly reduce the number of api functions and the supported options.
I have not taken into account any testing of the user-visible kernel data structures (because I don’t have any occurrence data).
Comments from readers with experience in testing OSes most welcome.
Another source of Linux specific information is the Linux Kernel documentation project. I don’t have any experience using this documentation, but the API documentation is very minimalist (automatically extracted from the source; the Assessment report lists this document as [D124], but never references it in the text).
Readers familiar with safety standards will be asking about the context in which this certification applies. Safety functions are not generic; they are specific to a safety-related system, i.e., software+hardware. This particular certification is for a Safety Element out of Context (SEooC), where “out of context” here means without the context of a system or knowledge of the safety goals. SEooC supports a bottom up approach to safety development, i.e., Safety Elements can be combined, along with the appropriate analysis and testing, to create a safety-related system.
This certification is the first of what I think will be many certifications of Linux, some at more rigorous safety levels.
Remotivating data analysed for another purpose
The motivation for fitting a regression model has a major impact on the model created. Some of the motivations include:
- practicing software developers/managers wanting to use information from previous work to help solve a current problem,
- researchers wanting to get their work published seeks to build a regression model that show they have discovered something worthy of publication,
- recent graduates looking to apply what they have learned to some data they have acquired,
- researchers wanting to understand the processes that produced the data, e.g., the author of this blog.
The analysis in the paper: An Empirical Study on Software Test Effort Estimation for Defense Projects by E. Cibir and T. E. Ayyildiz, provides a good example of how different motivations can produce different regression models. Note: I don’t know and have not been in contact with the authors of this paper.
I often remotivate data from a research paper. Most of the data in my Evidence-based Software Engineering book is remotivated. What a remotivation often lacks is access to the original developers/managers (this is often also true for the authors of the original paper). A complicated looking situation is often simplified by background knowledge that never got written down.
The following table shows the data appearing in the paper, which came from 15 projects implemented by a defense industry company certified at CMMI Level-3.
Proj Test Req Test Meetings Faulty Actual Scenarios
Plan Rev Env Scenarios Effort
Time Time
P1 144.5 1.006 85 60 100 2850 270
P2 25.5 1.001 25.5 4 5 250 40
P3 68 1.005 42.5 32 65 1966 185
P4 85 1.002 85 104 150 3750 195
P5 198 1.007 123 87 110 3854 410
P6 57 1.006 35 25 20 903 100
P7 115 1.003 92 55 56 2143 225
P8 81 1.009 156 62 72 1988 287
P9 388 1.004 150 208 553 13246 1153
P10 177 1.008 93 77 157 4012 360
P11 62 1.001 175 186 199 5017 310
P12 111 1.005 116 82 143 3994 423
P13 63 1.009 188 177 151 3914 226
P14 32 1.008 25 28 6 435 63
P15 167 1.001 177 143 510 11555 1133 |
where: TestPlanTime is the test plan creation time in hours, ReqRev is the test/requirements review of period in hours, TestEnvTime is the test environment creation time in hours, Meetings is the number of meetings, FaultyScenarios is the number of faulty test scenarios, Scenarios is the number of Scenarios, and ActualEffort is the actual software test effort.
Industrial data is hard to obtain, so well done to the authors for obtaining this data and making it public. The authors fitted a regression model to estimate software test effort, and the model that almost perfectly fits to actual effort is:
ActualEffort=3190 + 2.65*TestPlanTime
-3170*ReqRevPeriod - 3.5*TestEnvTime
+10.6*Meetings + 11.6*FaultScrenarios + 3.6*Scenarios |
My reading of this model is that having obtained the data, the authors felt the need to use all of it. I have been there and done that.
Why all those multiplication factors, you ask. Isn’t ActualTime simply the sum of all the work done? Yes it is, but the above table lists the work recorded, not the work done. The good news is that the fitted regression models shows that there is a very high correlation between the work done and the work recorded.
Is there a simpler model that can be used to explain/predict actual time?
Looking at the range of values in each column, ReqRev varies by just under 1%. Fitting a model that does not include this variable, we get (a slightly less perfect fit):
ActualEffort=100 + 2.0*TestPlanTime
- 4.3*TestEnvTime
+10.7*Meetings + 12.4*FaultScrenarios + 3.5*Scenarios |
Simple plots can often highlight patterns present in a dataset. The plot below shows every column plotted against every other column (code+data):

Points forming a straight line indicate a strong correlation, and the points in the top-right ActualEffort/FaultScrenarios plot look straight. In fact, this one variable dominates the others, and fits a model that explains over 99% of the deviation in the data:
ActualEffort=550 + 22.5*FaultScrenarios |
Many of the points in the ActualEffort/Screnarios plot are on a line, and adding Meetings data to the model explains just under 99% of the variance in the data:
actualEffort=-529.5
+15.6*Meetings + 8.7*Scenarios |
Given that FaultScrenarios is a subset of Screnarios, this connectedness is not surprising. Does the number of meetings correlate with the number of new FaultScrenarios that are discovered? Questions like this can only be answered by the original developers/managers.
The original data/analysis was interesting enough to get a paper published. Is it of interest to practicing software developers/managers?
In a small company, those involved are likely to already know what these fitted models are telling them. In a large company, the left hand does not always know what the right hand is doing. A CMMI Level-3 certified defense company is unlikely to be small, so this analysis may be of interest to some of its developer/managers.
A usable estimation model is one that only relies on information available when the estimation is needed. The above models all rely on information that only becomes available, with any accuracy, way after the estimate is needed. As such, they are not practical prediction models.
Deep dive looking for good enough reliability models
A previous post summarised the main highlights of my trawl through the software reliability research papers/reports/data, which failed to find any good enough models for estimating the reliability of a software system. This post summarises a deep dive into the technical aspects of the research papers.
I am now a lot more confident that better than worst case models for calculating software reliability don’t yet exist (perhaps the problem does not have a solution). By reliability, I mean the likelihood that a fault will be experienced during 1-hour of operation (1-hour is the time interval often used in safety critical standards).
All the papers assume that time to next new fault experience can be effectively modelled using timing information on the previously discovered distinct faults. Timing information might be cpu time, or elapsed time during testing or customer use, or even number of tests. Issues of code coverage and the correspondence between tests and customer usage are rarely mentioned.
Building a model requires making assumptions about the world. Given the data used, all the models assume that there is a relationship connecting the time between successive distinct faults, e,g, the Jelinski-Moranda model assumes that the time between fault experiences has an exponential distribution and that the exponent is the same for all faults. While the Jelinski-Moranda model does not match the behavior seen in the available datasets, it is widely discussed (its simplicity makes it a great example, with the analysis being straightforward and the result easy to explain).
Much of the fault timing data comes from the test process, with the rest coming from customer usage (either cpu or elapsed; like today’s cloud usage, mainframe time usage was often charged). What connection does a model fitted to data on the faults discovered during testing have with faults experienced by customers using the software? Managers want to minimise the cost of testing (one claimed use case for these models is estimating the likelihood of discovering a new fault during testing), and maximising the number of faults found probably has a higher priority than mimicking customer usage.
The early software reliability papers (i.e., the 1970s) invariably proposed a new model and then checked how well it fitted a small dataset.
While the top, must-read paper on software fault analysis was published in 1982, it has mostly remained unknown/ignored (it appeared as a NASA report written by non-academics who did not then promote their work). Perhaps if Nagel and Skrivan’s work had become widely known, today we might have a practical software reliability model.
Reliability research in the 1980s was dominated by theoretical analysis of the previously proposed models and their variants, finding connections between them and building more general models. Ramos’s 2009 PhD thesis contains a great overview of popular (academic) reliability models, their interconnections, and using them to calculate a number.
I did discover some good news. Researchers outside of software engineering have been studying a non-software problem whose characteristics have a direct mapping to software reliability. This non-software problem involves sampling from a population containing subpopulations of varying sizes (warning: heavy-duty maths), e.g., oil companies searching for new oil fields of unknown sizes. It looks, perhaps (the maths is very hard going), as-if the statisticians studying this problem have found some viable solutions. If I’m lucky, I will find a package implementing the technical details, or find a gentle introduction. Perhaps this thread will have a happy ending…
An aside: When quickly deciding whether a research paper is worth reading, if the title or abstract contains a word on my ignore list, the paper is ignored. One consequence of this recent detailed analysis is that the term NHPP has been added to my ignore list for software reliability issues (it has applicability for hardware).
Learning useful stuff from the Reliability chapter of my book
What useful, practical things might professional software developers learn from my evidence-based software engineering book?
Once the book is officially released I need to have good answers to this question (saying: “Well, I decided to collect all the publicly available software engineering data and say something about it”, is not going to motivate people to read the book).
This week I checked the reliability chapter; what useful things did I learn (combined with everything I learned during all the other weeks spent working on this chapter)?
A casual reader skimming the chapter would conclude that little was known about software reliability, and they would be right (I already knew this, but I learned that we know even less than I thought was known), and many researchers continue to dig in unproductive holes.
A reader with some familiarity with reliability research would be surprised to see that some ‘major’ topics are not discussed.
The train wreck that is machine learning has been avoided (not forgetting that the data used is mostly worthless), mutation testing gets mentioned because of some interesting data (the underlying problem is that mutation testing assumes that coding mistakes are local to one line, but in practice coding mistakes often involve multiple lines), and the theory discussions don’t mention non-homogeneous Poisson process as the basis for software fault models (because this process is not capable of solving the questions asked).
What did I learn? My highlights include:
- Anne Choa‘s work on population estimation. The takeaway from this work is that if people want to estimate the number of remaining fault experiences, based on previous experienced faults, then every occurrence (i.e., not just the first) of a fault needs to be counted,
- Phyllis Nagel and Janet Dunham’s top read work on software testing,
- the variability in the numeric percentage that people assign to probability terms (e.g., almost all, likely, unlikely) is much wider than I would have thought,
- the impact of the distribution of input values on fault experiences may be detectable,
- really a lowlight, but there is a lot less publicly available data than I had expected (for the other chapters there was more data than I had expected).
The last decade has seen fuzzing grow to dominate the headlines around software reliability and testing, and provide data for people who write evidence-based books. I don’t have much of a feel for how widely used it is in industry, but it is a very useful tool for reliability researchers.
Readers might have a completely different learning experience from reading the reliability chapter. What useful things did you learn from the reliability chapter?
Changes in the shape of code during the twenties?
At the end of 2009 I made two predictions for the next decade; Chinese and Indian developers having a major impact on the shape of code (ok, still waiting for this to happen), and scripting languages playing a significant role (got that one right, but then they were already playing a large role).
Since this blog has just entered its second decade, I will bring the next decade’s predictions forward a year.
I don’t see any new major customer ecosystems appearing. Ecosystems are the drivers of software development, and no new ecosystems has several consequences, including:
- No major new languages: Creating a language is a vanity endeavour. Vanity project can take off if they are in the right place at the right time. New ecosystems provide opportunities for new languages to become widely used by being in at the start and growing with the ecosystem. There is another opportunity locus; it is fashionable for companies that see themselves as thought-leaders to have their own language, e.g., Google, Apple, and Mozilla. Invent your language at the right time, while working for a thought-leader company and your language could become well-known enough to take-off.
I don’t see any major new ecosystems appearing, and all the likely companies already have their own language.
Any new language also faces the problem of not having a large collection packages.
- Software will be more thoroughly tested: When an ecosystem is new, the incentives drive early and frequent releases (to build a customer base); software just has to be good enough. Once a product is established, companies can invest in addressing issues that customers find annoying, like faulty behavior; the incentive change results in more testing.
There are other forces at work around testing. Companies are experiencing some very expensive faults (testing may be expensive, but not testing may be more expensive) and automatic test generation is becoming commercially usable (i.e., the cost of some kinds of testing is decreasing).
The evolution of widely used languages.
- I think Fortran and C will have new features added, with relatively little fuss, and will quietly continue to be widely used (to the dismay of the fashionista).
-
There is a strong expectation that C++ and Java should continue to evolve:
- I expect the ISO C++ work to implode, because there are too many people pulling in too many directions. It makes sense for the gcc and llvm teams to cooperate in taking C++ in a direction that satisfies developers’ needs, rather than the needs of bored consultants. What are Microsoft’s views? They only have their own compiler for strategic reasons (they make little if any profit selling compilers, compilers are an unnecessary drain on management time; who cares what happens to the language).
- It is going to be interesting watching the impact of Oracle’s move to charging for runtimes. I have no idea what might happen to Java.
In terms of code volume, the future surely has to be scripting languages, and in particular Python, Javascript and PHP. Ten years from now, will there be a widely used, single language? People have been predicting, for many years, that web languages will take over the world; perhaps there will be a sudden switch and I will see that the choice is obvious.
Moore’s law is now dead, which means researchers are going to have to look for completely new techniques for building logic gates. If photonic computers happen, then ternary notation may reappear again (it was used in at least one early Russian computer); I’m not holding my breath for this to occur.
Distorting the input profile, to stress test a program
A fault is experienced in software when there is a mistake in the code, and a program is fed the input values needed for this mistake to generate faulty behavior.
There is suggestive evidence that the distribution of coding mistakes and inputs generating fault experiences both have an influence of fault discovery.
How might these coding mistakes be found?
Testing is one technique, it involves feeding inputs into a program and checking the resulting behavior. What are ‘good’ input values, i.e., values most likely to discover problems? There is no shortage of advice for manually writing tests, suggesting how to select input values, but automatic generation of inputs is often somewhat random (relying on quantity over quality).
Probabilistic grammar driven test generators are trivial to implement. The hard part is tuning the rules and the probability of them being applied.
In most situations an important design aim, when creating a grammar, is to have one rule for each construct, e.g., all arithmetic, logical and boolean expressions are handled by a single expression rule. When generating tests, it does not always make sense to follow this rule; for instance, logical and boolean expressions are much more common in conditional expressions (e.g., controlling an if-statement), than other contexts (e.g., assignment). If the intent is to mimic typical user input values, then the probability of generating a particular kind of binary operator needs to be context dependent; this might be done by having context dependent rules or by switching the selection probabilities by context.
Given a grammar for a program’s input (e.g., the language grammar used by a compiler), decisions have to be made about the probability of each rule triggering. One way of obtaining realistic values is to parse existing input, counting the number of times each rule triggers. Manually instrumenting a grammar to do this is a tedious process, but tool support is now available.
Once a grammar has been instrumented with probabilities, it can be used to generate tests.
Probabilities based on existing input will have the characteristics of that input. A recent paper on this topic (which prompted this post) suggests inverting rule probabilities, so that common becomes rare and vice versa; the idea is that this will maximise the likelihood of a fault being experienced (the assumption is that rarely occurring input will exercise rarely executed code, and such code is more likely to contain mistakes than frequently executed code).
I would go along with the assumption about rarely executed code having a greater probability of containing a mistake, but I don’t think this is the best test generation strategy.
Companies are only interested in fixing the coding mistakes that are likely to result of a fault being experienced by a customer. It is a waste of resources to fix a mistake that will never result in a fault experienced by a customer.
What input is likely to interact with coding mistakes to be the root cause of faults experienced by a customer? I have no good answer to this question. But, given there are customer input contains patterns (at least in the world of source code, and I’m told in other application domains), I would generate test cases that are very similar to existing input, but with one sub-characteristic changed.
In the academic world the incentive is to publish papers reporting loads-of-faults-found, the more the merrier. Papers reporting only a few faults are obviously using inferior techniques. I understand this incentive, but fixing problems costs money and companies want a customer oriented rationale before they will invest in fixing problems before they are reported.
The availability of tools that automate the profiling of a program’s existing input, followed by the generation of input having slightly, or very, different characteristics make it easier to answer some very tough questions about program behavior.
Top, must-read paper on software fault analysis
What is the top, must read, paper on software fault analysis?
Software Reliability: Repetitive Run Experimentation and Modeling by Phyllis Nagel and James Skrivan is my choice (it’s actually a report, rather than a paper). Not only is this report full of interesting ideas and data, but it has multiple replications. Replication of experiments in software engineering is very rare; this work was replicated by the original authors, plus Scholz, and then replicated by Janet Dunham and John Pierce, and then again by Dunham and Lauterbach!
I suspect that most readers have never heard of this work, or of Phyllis Nagel or James Skrivan (I hadn’t until I read the report). Being published is rarely enough for work to become well-known, the authors need to proactively advertise the work. Nagel, Dunham & co worked in industry and so did not have any students to promote their work and did not spend time on the academic seminar circuit. Given enough effort it’s possible for even minor work to become widely known.
The study run by Nagel and Skrivan first had three experienced developers independently implement the same specification. Each of these three implementations was then tested, multiple times. The iteration sequence was: 1) run program until fault experienced, 2) fix fault, 3) if less than five faults experienced, goto step (1). The measurements recorded were fault identity and the number of inputs processed before the fault was experienced.
This process was repeated 50 times, always starting with the original (uncorrected) implementation; the replications varied this, along with the number of inputs used.
For a fault to be experienced, there has to be a mistake in the code and the ‘right’ input values have to be processed.
How many input values need to be processed, on average, before a particular fault is experienced? Does the average number of inputs values needed for a fault experience vary between faults, and if so by how much?
The plot below (code+data) shows the numbers of inputs processed, by one of the implementations, before individual faults were experienced, over 50 runs (sorted by number of inputs):
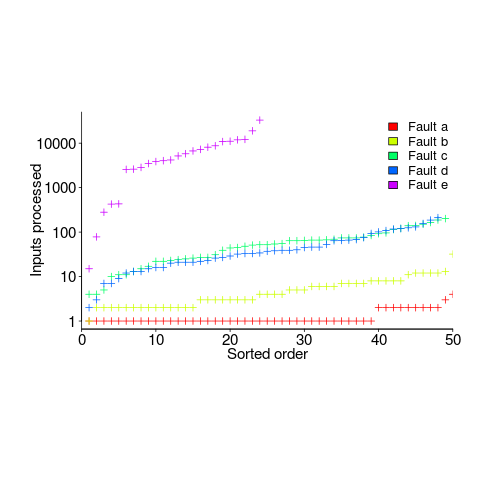
Different faults have different probabilities of being experienced, with fault a being experienced on almost any input and fault e occurring much less frequently (a pattern seen in the replications). There is an order of magnitude variation in the number of inputs processed before particular faults are experienced (this pattern is seen in the replications).
Faults were fixed as soon as they were experienced, so the technique for estimating the total number of distinct faults, discussed in a previous post, cannot be used.
A plot of number of faults found against number of inputs processed is another possibility. More on that another time.
Suggestions for top, must read, paper on software faults, welcome (be warned, I think that most published fault research is a waste of time).
Statement sequence length for error/non-error paths
One of the folk truisms of the compiler/source code analysis business is that error paths are short, i.e., when an error situation is detected (such as failing to open a file), few statements are executed before the functions returns.
Having repeated this truism for many decades, figure 2 from the paper APEx: Automated Inference of Error Specifications for C APIs jumped off the page at me; thanks to Yuan Kang, I now have a copy of the data.
The plots below (code+data) show two representations of the non-error/error path lengths (measured in statements within individual functions of libc; counting starts at a library call that could return an error value). The upper plot shows statement sequence lengths for error/non-error paths, and the lower is a kernel density plot of the error/non-error sequence lengths.
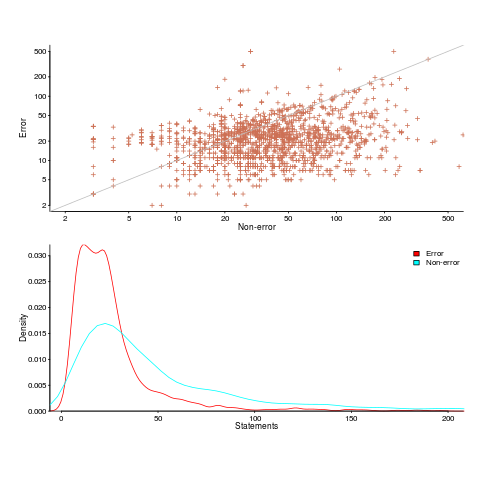
Another truism is that people tend to write positive tests, i.e., tests that do not involve error handling (some evidence).
Code coverage measurements (e.g., number of statements or branches that are executed by a test suite) often show the pattern seen in the plot below (code+data; thanks to the authors of the paper Code Coverage for Suite Evaluation by Developers for making the data available). The data was obtained by measuring the coverage of 1,043 Java programs executing their associated test suite (circles denote program size). Lines are fitted regression models for different sized programs.
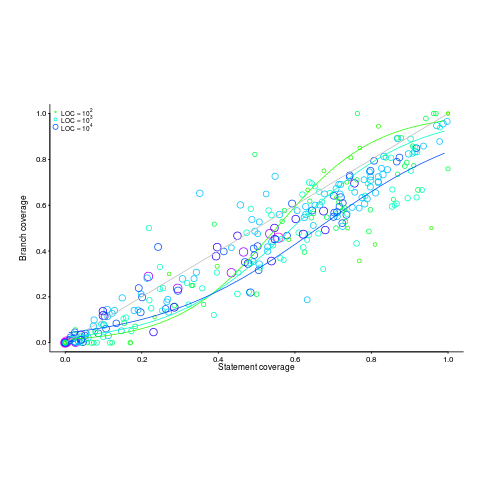
If people are preferentially writing positive tests, test suites with low coverage would be expected to execute a greater percentage of statements than branches (an if-statement has two branches, taken/not-taken), i.e., the behavior seen in the plot above (grey line shows equal statement/branch coverage). Once the low hanging fruit is tested (i.e., the longer, non-error, cases), tests have to be written for the shorter, more likely to be error handling, cases.
The plot would also be explained by typical execution paths favoring longer basic blocks, but I don’t have any data that could show this one way or another.
Spreadsheet errors: open source or survival of the fittest
There is a bit of a kerfuffle going on in the economics world at the moment over spreadsheet errors and data cherry-picking in an influential paper about the current economic crisis. I don’t know anything about economics and will leave commentary on the data cherry-picking to others, but I can claim to know something about coding errors.
Stories of companies loosing lots of money because of small mistakes in a spreadsheet are fairly common, this problem is not rare or unimportant. Academic research on spreadsheets seems to be slowly gathering steam, with PhDs appearing every now and again. Industry appears to be more active, with a variety of companies offering tools aimed at finding faults in spreadsheets.
Based on my somewhat limited experience of helping people fix spreadsheet problems, I suspect that no amount of research or tool availability from industry will solve the real problem that faces spreadsheet users, which is that they don’t appreciate their own fallibility.
Back when software development first started, people were very surprised to discover the existence of software faults. As every new programmer discovers, computers are merciless and will punish the slightest coding mistake. A large part of becoming a professional developer involves learning how to structure development to deal with personal fallibility, plus developing a mental attitude capable of handling the constant reminder of personal fallibility that computers provide to anybody writing code to tell them what to do (something that deters some people from becoming developers).
It rarely enters the head’s of people who are sporadic authors of code or spreadsheets that they may be making subtle mistakes that can have a significant impact on the results produced. Getting somebody with this frame of mind to perform testing on what they have written is well-nigh on impossible.
In a research context one very practical solution to the code reliability issue is to insist that code or/and spreadsheets be made freely available. Only when the spreadsheet used to create the results in the paper linked to above was made available to others were the mistakes it contained uncovered.
In a commercial context it is down to survival of the fittest, those companies who do not keep their spreadsheet errors below a recoverable level die.
Low defect density implies climate code less, not more, reliable
I have just been reading a paper comparing the defect density of three climate modelling systems against software from other application domains. The defect density (total reported defects divided by thousands of lines of code) of the climate modelling software was significantly lower than everything else, leading the researchers to conclude that “… suggests that the models are of high software quality,”. I would draw the opposite conclusion, the models have low reliability (I have no idea what software quality is and avoid using the term).
I don’t disagree with Pipitone and Easterbrook numbers, just their conclusion.
There is a very simple technique for creating software that has a low defect density, don’t try too hard to look for defects. There are two reasons why I think this has happened with the climate model software:
- Three of the non-climate systems compared against were the Apache HTTP demon, the VTK visulalization toolkit and the Eclipse project. These are all widely used projects with many thousands of users, millions for Apache; this volume of usage corresponds to a huge amount of testing, and it is no wonder that so many faults have been reported. Each climate model tends to be used by one site, a tiny amount of testing, and it is not surprising that few faults have been reported.
- Climate models have a big intrinsic testing problem; what is the result of a test supposed to be? With applications such as word processors, browsers, compilers, operating systems, etc the expected behavior is known in many cases so it is possible to write test cases that check for the expected behavior. How does anybody know what the expected behavior of a climate model is? If all the climate models did was to solve the Navier-Stokes equation on a rotating sphere there would be no need for multiple models and the UK Meteorological Office’s Unified model would not have grown from 100 KLOC to 800+ KLOC over the last 15 years.
The one system having a similar defect density to the climate models that Pipitone and Easterbrook compare against is an air traffic control system developed using formal methods, exactly the kind of (expensive and time-consuming) development process that one would expect to have a low defect density.
Software is remarkably fault-tolerant and so, yes, serious fault could exist in the climate models and they would still give answers that looked about right. Based on his experience working on a meteorological model Les Hatton tells the story of a fault so serious that the answers should be completely wrong, but they were not.
If somebody wants to convince me that the software in any of these climate models really is reliable then I want to know about the test suites used to check the behavior; what coverage of the source does the suite have (a high MC/DC would be very good, but I would settle for a very high statement coverage) and how were the expected behaviors calculated.
Recent Comments