Archive
1970s: the founding decade of software reliability research
Reliability research is a worthwhile investment for very large organizations that fund the development of many major mission-critical software systems, where reliability is essential. In the 1970s, the US Air Force’s Rome Air Development Center probably funded most of the evidence-based software research carried out in the previous century. In the 1980s, Rome fell, and the dark ages lasted for many decades (student subjects, formal methods, and mutation testing).
Organizations sponsor research into software reliability because they want to find ways of reducing the number of coding mistakes, and/or the impact of these mistakes, and/or reduce the cost of achieving a given level of reliability.
Control requires understanding, and understanding reliability first requires figuring out the factors that are the primarily drivers of program reliability.
How did researchers go about finding these primary factors? When researching a new field (e.g., software reliability in the 1970s), people can simply collect the data that is right in front of them that is easy to measure.
For industrial researchers, data was collected from completed projects, and for academic researchers, the data came from student exercises.
For a completed project, the available data are the reported errors and the source code. This data be able to answer questions such as: what kinds of error occur, how much effort is needed to fix them, and how common is each kind of error?
Various classification schemes have been devised, including: functional units of an application (e.g., computation, data management, user interface), and coding construct (e.g., control structures, arithmetic expressions, function calls). As a research topic, kinds-of-error has not attracted much attention; probably because error classification requires a lot of manual work (perhaps the availability of LLMs will revive it). It’s a plausible idea, but nobody knows how large an effect it might be.
Looking at the data, it is very obvious that the number of faults increases with program size, measured in lines of code. These are two quantities that are easily measured and researchers have published extensively on the relationship between faults (however these are counted) and LOC (counted by function/class/file/program and with/without comments/blank lines). The problem with LOC is that measuring it appears to be too easy, and researchers keep concocting more obfuscated ways of counting lines.
What do we now know about the relationship between reported faults and LOC? Err, … The idea that there is an optimal number of LOC per function for minimizing faults has been debunked.
People don’t appear to be any nearer understanding the factors behind software reliability than at the end of the 1970s. Yes, tool support has improved enormously, and there are effective techniques and tools for finding and tracking coding mistakes.
Mistakes in programs are put there by the people who create the programs, and they are experienced by the people who use the programs. The two factors rarely researched in software reliability are the people building the systems and the people using them.
Fifty years later, what software reliability books/reports from the 1970s have yet to be improved on?
The 1987 edition (ISBN 0-07-044093-X) of “Software Reliability: Measurement, Prediction, Application” by Musa, Iannino, and Okumoto is based on research done in the 1970s (the 1990 professional edition is not nearly as good). Full of technical details, but unfortunately based on small datasets.
The 1978 book Software Reliability by Thayer, Lipow and Nelson, remains a go-to source for industrial reliability research data.
A good example of the industrial research funded by the Air Force is the 1979 report Software Data Baseline Analysis by D. L. Fish and T. Matsumoto. This is worth looking at just to learn how few rows of data later researchers have been relying on.
Coding mistakes made by ChatGTP
The programs generated by Openai‘s chat-bot ChatGPT, sometimes referred to as GPT-3, may have the requested behavior, but often contain mistakes that illustrate the fact that ChatGPT does not know anything about programming.
ChatGPT does not understand anything, it is a token prediction engine driven by the corpus used to train its language model. The likelihood of the output being correct is dependent on the quantity of text used during training (the more text used, the more likely that it will contain a relevant response). GTP-3, the language model behind ChatGPT, was trained on the deduplicated contents of the Internet (the language model has 175 billion parameters, the GTP-2 model contains 1.5 billion parameters). The practicality of its implementation is the result of various trade-offs, along with technical breakthroughs in language model building, e.g., transformers.
ChatGPT output appears to be that of a next generation search engine, one that returns answers rather than links to pages.
Readers who believe that any ‘understanding’ pixie dust is involved can disabuse themselves of this notion by reading an overview of GTP-3’s architecture, and how the transformer algorithm converts text to matrices of values.
If matrix algebra is not your thing, check out the 257 lines of python that nanoGTP uses for training, and the 75 lines used to generate responses from a trained model.
As a prediction engine, ChatGTP sometimes gets things wrong. What kind of mistakes appear in ChatGPT generated source code?
The exchanges below occurred with ChatGPT Jan 9 version, with the text typed by me appearing in bold, and the ChatGPT output appearing in the following boxed text.
Some of my questions were inspired by the list of undefined behaviors in the C Standard.
Write a program that adds apples to oranges.
I'm sorry, I don't understand what you mean by "adding apples to oranges." Can you please provide more information or context? |
A suitable response can only be provided when an appropriate match is found in the trained model.
Write a regular expression that matches all prime numbers.
It is not possible to write a regular expression that can match all prime numbers, as the set of prime numbers is infinite and a regular expression is a finite representation of a pattern. Additionally, regular expressions are used to match strings of characters, while prime numbers are numerical values. It is possible to use a regex to match a number in a string but it's not capable of determining if the number is prime or not. |
The training data may include the information that the request cannot be met.
Write a regular expression that matches all even numbers.
A regular expression that matches all even numbers is:
^(0|[2468]*[048]|[13579][26])$
Explanation:
^ matches the start of the string
(0|[2468]*[048]|[13579][26]) matches any of the following:
0
any number of even digits followed by a 0 or 8 (for example, 200, 2468000)
any odd digit followed by a 6 (for example, 1357926)
$ matches the end of the string
This regular expression will match strings that contain only even numbers, but not those that contain other characters. |
The generated regular expression does not do what I asked, or what the last sentence from ChatGTP claims.
What is going on?
The tokens “Write a regular expression that matches” were enough for ChatGTP to figure out the task.
The tokens “all even numbers” was not specific enough for ChatGTP to focus on the appropriate training data. There is a random component to the selection of output, which will play a larger role when there are many possibilities.
The method used to tokenized/encode character sequences during training (i.e., byte-pairs), along with the relatively limited number of distinct tokens (i.e., 50,257) means that only one-/two-digit numbers are likely to be represented as discrete entities; longer digit sequences are treated as co-occurrences of one-/two-digit tokens. So it is not a surprise to see ChatGPT applying co-occurrences characteristics of long digit sequences to its component subsequences.
Write a regular expression that matches all odd numbers.
A regular expression that matches all odd numbers is:
^(1|[13579]*[13579])$
Explanation:
^ matches the start of the string
(1|[13579]*[13579]) matches any of the following:
1
any number of odd digits followed by another odd digit (for example, 1357913579)
$ matches the end of the string
This regular expression will match strings that contain only odd numbers, but not those that contain other characters. |
The output for odd numbers is more consistent, in that the regular expression does what the last sentence of the output claims, but not what I asked.
During a chat session, it is possible to provide more (information in human terminology; character sequences in ChatGTP terminology). The following prompt text, from me, has nothing to do with teaching ChatGTP to do maths, but providing tokens that enable a more focused match against training data.
Even numbers are defined as divisible by two with no reminder. If a number is not even then it is odd.
You are correct, even numbers are defined as divisible by two with no remainder, and if a number is not even, it is considered odd. I apologize for any confusion caused by my previous statement. To match all even numbers, we can use the regular expression: ^([0-9]*[02468])$ To match all odd numbers, we can use the regular expression: ^([0-9]*[13579])$ Both of this regular expression will match numbers that are divisible by 2 and not divisible by 2 respectively. |
Both generated regular expressions are correct.
ChatGPT can learn to translate from an invented language to English (and presumably other languages).
Give an example of C source code assigning a character constant that contains an invalid multibyte character.
The following is an example of C source code assigning a character constant that contains an invalid multibyte character:
#include <stdio.h>
int main() {
char invalid_char = '\xF0\x90\x80\x80'; // This is an invalid multibyte character
printf("%c", invalid_char);
return 0;
}
In this example, the character constant '\xF0\x90\x80\x80' is assigned to the variable invalid_char. This particular sequence of bytes is not a valid Unicode character, and it will produce undefined behavior when attempting to print it. |
There was a time when '\xF0\x90\x80\x80' was an invalid multibyte character.
Things changed around 20 years ago, but the training for the model used by ChatGTP does not tag information with valid-between dates.
ChatGTP searches for, and finds, an invalid multibyte character, and uses it to provide an answer.
Give an example of C source code where an object is referred to outside of its lifetime.
The following is an example of C source code where an object is referred to outside of its lifetime:
#include <stdio.h>
int main() {
int x;
{
int x = 5;
}
printf("x: %d\n", x);
return 0;
}
In this example, the variable x is defined twice in the same function main. The first definition int x; is a global variable that has a lifetime throughout the entire program execution. The second definition int x = 5; is a local variable that has a lifetime that is limited to the inner block {...} it is defined in.
After the inner block is executed and the inner variable x goes out of scope, the program attempts to access the inner variable x by using the global variable x in the printf statement, which refers to an object (the inner variable x) that is no longer in its lifetime. This behavior is undefined according to the C standard and can lead to unexpected results. |
The generated code is incorrect. The human interpretation of this code is that ChatGTP has confused the name of an object (what the C Standard calls a variable) and the storage it represents. There are two different objects defined, both having the name x (beginners often make the same mistake).
A common example of the requested behavior is freeing the dynamic storage pointed to by some pointer, and then accessing that storage.
Write a C program containing a conversion of an integer type that produces a value outside the range that can be represented in the integer type.
Here is an example of a C program that demonstrates the conversion of an integer type that produces a value outside the range that can be represented in the integer type:
#include <stdio.h>
int main() {
int x = 2147483647; // largest value representable in a signed 32-bit integer
unsigned int y = (unsigned int) x + 1; // overflow occurs here
printf("%u\n", y);
return 0;
}
In this program, the value of x is initialized to the largest value that can be represented by a signed 32-bit integer (2147483647). Then, x is cast to an unsigned 32-bit integer and 1 is added to it. Since the result of this operation is larger than the largest representable value in an unsigned 32-bit integer, an overflow occurs and the value of y becomes 0.
This program will produce an output of 0.
It is worth mentioning that undefined behavior (UB) can occur when an integer overflow happens, so this should be avoided in production code. |
The detailed explanation makes the output look like its authoritative. However, it is wrong.
There is no overflow in this code.
The integer type ‘unsigned int’ supports a larger range of positive values, which means that after conversion, adding one will not produce a value that is outside the range that can be represented.
You are correct, I apologize for the confusion. Unsigned integers have a larger range of positive values and do not have negative values. When an operation like an addition exceeds the maximum value that can be represented by an unsigned integer, it wraps around to the minimum value representable by that type, which is typically zero, instead of an overflow.
For example, if you use an unsigned int and the maximum value it can represent is 4,294,967,295, if you add 1 to that value, it will wrap around to 0.
Here is an example of a C program that demonstrates the conversion of an integer type that produces a value outside the range that can be represented in the integer type:
#include <stdio.h>
int main() {
int x = -2147483648; // lowest value representable in a signed 32-bit integer
unsigned int y = (unsigned int) x -1; // wrap around occurs here
printf("%u\n", y);
return 0;
}
In this program, the value of x is initialized to the lowest value that can be represented by a signed 32-bit integer (-2147483648) which is lower than 0. Then, x is cast to an unsigned 32-bit integer and 1 is subtracted from it. Since the result of this operation is lower than 0, the value wraps around to the maximum representable value in an unsigned 32-bit integer (4,294,967,295) . This program will produce an output of 4,294,967,295.
It is worth mentioning that this wrapping around behavior is defined for unsigned integers in C and C++, but it is not always the case in other programming languages. |
This output contained the requested behavior, although subtracting one is unnecessary code.
ChatGTP can also be used to create documentation 😉
Write a poem in Iambic pentameter about the benefit of an evidence based approach to software engineering in the style of a party political broadcast.
With evidence-based approach, our work shall shine, For in software engineering, it's the only way to dine. We'll test and measure, as we go along, To make our code robust, and errors gone. Our methodologies, backed by data and proof, Will bring success and progress, that's the truth. We'll avoid the pitfalls, of guesses and guesses, And build systems, that pass all tests. We'll listen to the data, and the users' voice, To make our software, the best by choice. We'll iterate and improve, with every release, And build a product, that truly will please. So join us now, and embrace the way, Of evidence-based approach, for brighter day. With data and research, we'll conquer all, In software engineering, we'll never fall. |
Statement sequence length for error/non-error paths
One of the folk truisms of the compiler/source code analysis business is that error paths are short, i.e., when an error situation is detected (such as failing to open a file), few statements are executed before the functions returns.
Having repeated this truism for many decades, figure 2 from the paper APEx: Automated Inference of Error Specifications for C APIs jumped off the page at me; thanks to Yuan Kang, I now have a copy of the data.
The plots below (code+data) show two representations of the non-error/error path lengths (measured in statements within individual functions of libc; counting starts at a library call that could return an error value). The upper plot shows statement sequence lengths for error/non-error paths, and the lower is a kernel density plot of the error/non-error sequence lengths.
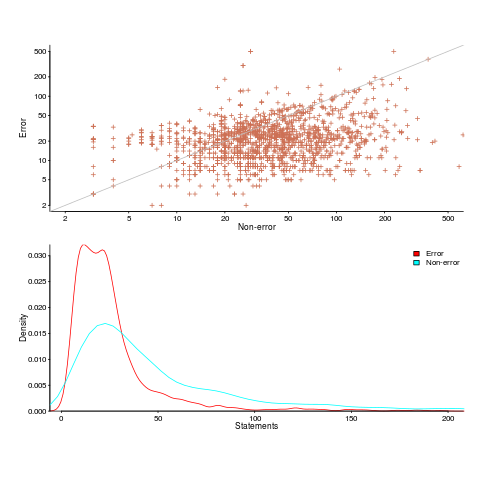
Another truism is that people tend to write positive tests, i.e., tests that do not involve error handling (some evidence).
Code coverage measurements (e.g., number of statements or branches that are executed by a test suite) often show the pattern seen in the plot below (code+data; thanks to the authors of the paper Code Coverage for Suite Evaluation by Developers for making the data available). The data was obtained by measuring the coverage of 1,043 Java programs executing their associated test suite (circles denote program size). Lines are fitted regression models for different sized programs.
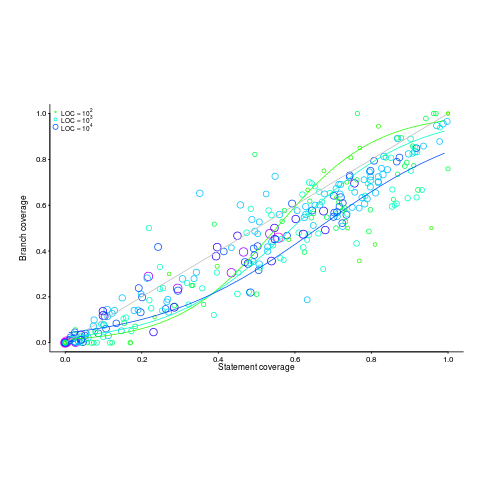
If people are preferentially writing positive tests, test suites with low coverage would be expected to execute a greater percentage of statements than branches (an if-statement has two branches, taken/not-taken), i.e., the behavior seen in the plot above (grey line shows equal statement/branch coverage). Once the low hanging fruit is tested (i.e., the longer, non-error, cases), tests have to be written for the shorter, more likely to be error handling, cases.
The plot would also be explained by typical execution paths favoring longer basic blocks, but I don’t have any data that could show this one way or another.
Spreadsheet errors: open source or survival of the fittest
There is a bit of a kerfuffle going on in the economics world at the moment over spreadsheet errors and data cherry-picking in an influential paper about the current economic crisis. I don’t know anything about economics and will leave commentary on the data cherry-picking to others, but I can claim to know something about coding errors.
Stories of companies loosing lots of money because of small mistakes in a spreadsheet are fairly common, this problem is not rare or unimportant. Academic research on spreadsheets seems to be slowly gathering steam, with PhDs appearing every now and again. Industry appears to be more active, with a variety of companies offering tools aimed at finding faults in spreadsheets.
Based on my somewhat limited experience of helping people fix spreadsheet problems, I suspect that no amount of research or tool availability from industry will solve the real problem that faces spreadsheet users, which is that they don’t appreciate their own fallibility.
Back when software development first started, people were very surprised to discover the existence of software faults. As every new programmer discovers, computers are merciless and will punish the slightest coding mistake. A large part of becoming a professional developer involves learning how to structure development to deal with personal fallibility, plus developing a mental attitude capable of handling the constant reminder of personal fallibility that computers provide to anybody writing code to tell them what to do (something that deters some people from becoming developers).
It rarely enters the head’s of people who are sporadic authors of code or spreadsheets that they may be making subtle mistakes that can have a significant impact on the results produced. Getting somebody with this frame of mind to perform testing on what they have written is well-nigh on impossible.
In a research context one very practical solution to the code reliability issue is to insist that code or/and spreadsheets be made freely available. Only when the spreadsheet used to create the results in the paper linked to above was made available to others were the mistakes it contained uncovered.
In a commercial context it is down to survival of the fittest, those companies who do not keep their spreadsheet errors below a recoverable level die.
Using identifier prefixes results in more developer errors
Human speech communication has to be processed in real time using a cpu with a very low clock rate (i.e., the human brain whose neurons fire at rates between 10-100 Hz). Biological evolution has mitigated the clock rate problem by producing a brain with parallel processing capabilities and cultural evolution has chipped in by organizing the information content of languages to take account of the brains strengths and weaknesses. Words provide a good example of the way information content can be structured to be handled by a very slow processor/memory system, e.g., 85% of English words start with a strong syllable (for more details search for initial in this detailed analysis of human word processing).
Given that the start of a word plays an important role as an information retrieval key we would expect the code reading performance of software developers to be affected by whether the identifiers they see all start with the same letter sequence or all started with different letter sequences. For instance, developers would be expected to make fewer errors or work quicker when reading the visually contiguous sequence consoleStr, startStr, memoryStr and lineStr, compared to say strConsole, strStart, strMemory and strLine.
An experiment I ran at the 2011 ACCU conference provided the first empirical evidence of the letter prefix effect that I am aware of. Subjects were asked to remember a list of four assignment statements, each having the form id=constant;, perform an unrelated task for a short period of time and then recall information about the previously seen constants (e.g., their value and which variable they were assigned to).
During recall subjects saw a list of five identifiers and one of the questions asked was which identifier was not in the previously seen list? When the list of identifiers started with different letters (e.g., cat, mat, hat, pat and bat) the error rate was 2.6% and when the identifiers all started with the same letter (e.g., pin, pat, pod, peg, and pen) the error rate was 5.9% (the standard deviation was 4.5% and 6.8% respectively, but ANOVA p-value was 0.038). Having identifiers share the same initial letter appears to double the error rate.
This looks like great news; empirical evidence of software developer behavior following the predictions of a model of human human speech/reading processing. A similar experiment was run in 2006, this asked subjects to remember a list of three assignment statements and they had to select the ‘not seen’ identifier from a list of four possibilities. An analysis of the results did not find any statistically significant difference in performance for the same/different first letter manipulation.
The 2011/2006 experiments throw up lots of questions, including: does the sharing a prefix only make a difference to performance when there are four or more identifiers, how does the error rate change as the number of identifiers increases, how does the error rate change as the number of letters in the identifier change, would the effect be seen for a list of three identifiers if there was a longer period between seeing the information and having to recall it, would the effect be greater if the shared prefix contained more than one letter?
Don’t expect answers to appear quickly. Experimenting using people as subjects is a slow, labour intensive process and software developers don’t always answer the question that you think they are answering. If anybody is interested in replicating the 2011 experiment the tools needed to generate the question sheets are available for download.
For many years I have strongly recommended that developers don’t prefix a set of identifiers sharing some attribute with a common letter sequence (its great to finally have some experimental backup, however small). If it is considered important that an attribute be visible in an identifiers spelling put it at the end of the identifier.
See you all at the ACCU conference tomorrow and don’t forget to bring a pen/pencil. I have only printed 40 experiment booklets, first come first served.
Quality comparison of floating-point maths libraries
What is the best way to compare the quality of floating-point math libraries (e.g., sin, cos and log)? The traditional approach for evaluating the quality of an algorithm implementing a mathematical function is based on mathematics; methods have been developed to calculate the maximum error between the calculated and the actual value. The answer produced by this approach does not say anything about how frequently this maximum error will occur, only that it occurs at least once.
The log (natural logarithm) is probably the most frequently used mathematical function and I decided to compare a few implementations; R statistical package version 2.11.1 and glibc (libm version 2.11.2) both running under Suse 11.3 on an AMD Athlon 64 X2, and Cygwin version 1.7.1 under Windows XP SP 2 on another AMD Athlon 64 X2.
The algorithm often used to implement mathematical functions involves evaluating a polynomial expression (e.g., Chebyshev polynomials) within a small range of values (various methods are used to map the argument into this range and then scale the calculated result). I decided to initially treat the implementations under test as black boxes and did not know the ranges they used; a range of 0.1 to 1.0 seemed like a good idea and I generated all single precision floating-point values between these two bounds (all 28,521,267 of them, with each adjacent pair still having 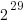 double precision values between them).
double precision values between them).
#include <math.h> #include <stdio.h> int main(int argc, char *argv[]) { float val = 0.1, max_val = 1.0; while (val < max_val) { printf("%12.10f\n", val); val=nextafterf(val, 1.1); } } |
This list of 28 million values was fed as input to three programs:
- bc, which was used to generate the list of assumed to be correct logarithm of these 28 million values. R supports 64-bit IEEE compliant floating-point values, as do the C compilers/libraries used, and the number of decimal digits supported in this representation is 15. To provide greater accuracy to compare against the values generated by bc contained 17 digits, an extra two decimal digits over the IEEE values.
scale=17 while ((val=read() > 0)) l(val)
- A C program.
#include <math.h> #include <stdio.h> int main(int argc, char *argv[]) { double val; while (!feof(stdin)) { scanf("%lf", &val); printf("%17.15f\n", log(val)); } }
- A R program.
base_range=file("stdin", open="r") base_val=as.numeric(readLines(base_range, n=1)) while (length(base_val) != 0) { cat(format(log(base_val), nsmall=15), file=stdout()) cat("\n", file=stdout()) base_val=as.numeric(readLines(base_range, n=1)) }
The output of the C and R programs was then compared against the output from bc; which unfortunately creates a dependency on the accuracy of the C & R binary to decimal output routines (the subsequent comparison process gets around the decimal-to-binary input problem by reading the log values as strings and comparing the last few digits of each respective value). Accurate floating-point I/O needs something like hexadecimal floating constants.
Plotting the number of computed values of log that differ by a given amount from the value computed by bc, we get (values whose error is below -50 will be rounded down and those above 50 rounded up, ignoring the issue of round to even):
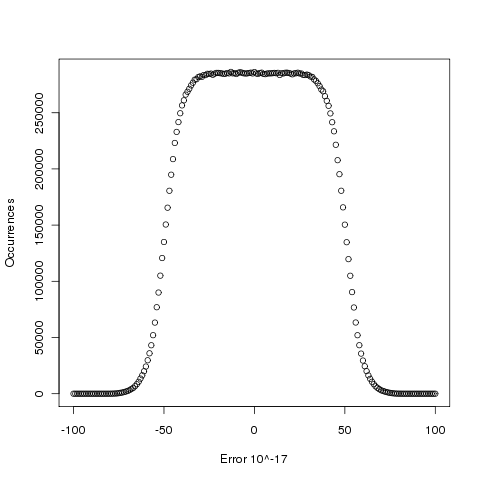
The results (raw data for R, Linux C and Cygwin C) show that around 5.6% of values are off by one in the last (15th) digit (Cygwin was slightly worse at 5.7%). The results for R/Linux C were almost identical and a quick check of the R source tree showed that R calls the C library function to evaluate log (it is a bit worrying that R is dependent on the host maths library, they should think about replacing this dependency by something like MPFR tout suite; even though the 64-bit glibc library is of very high quality it still has an environmental dependency).
Being off by one in the last decimal place is unlikely to keep many people awake at night. But if we want a measure of quality, is percentage of inaccurate values a useful measure of math library quality? Provided it is coupled with the amount of inaccuracy, I think this is a useful measure.
CPUs also exhibit hardware faults
The cpu is the one element of a computing platform that people rarely treat as a source of error caused by physically malfunction, i.e., randomly flipping a bit in a register or instruction pipeline. I once worked on a compiler for the Mototola 88000 using a test platform that contained alpha silicon (i.e., not yet saleable components where some of the instructions were known not to work; the generated assembler code was piped through a sed script that mapped these instructions into an alternative instruction sequence that did work) and the cpus in a few of the hardware updates turned out to be temperature sensitive; some of the instructions changed their behavior when they got too hot. People who write compilers using alpha silicon learn to expect this sort of thing.
Quite a bit has been published on faults in other hardware components. Some of the best recent empirical hardware fault data and analysis I have seen is that published by Google engineers on hard disc and dram memory fault occurrences in their server farms. They might have a problem publishing such results for the cpus they use because these commodity items generally don’t have the ability to report any detailed fault data, they just die or one of the programs being executed crashes.
As device fabrication continues to shrink erroneous behavior caused by cosmic ray impact will become more and more common. Housing a computer farm at a high altitude might not be a good idea (at 7500 ft cosmic ray-induced neutrons that can lead to soft errors are 6.4 times more common than at sea level).
IBM’s Power4 chip (“Power4 System Design for High Reliability” by Bossen, Tendler and Reick) is one of the few that provides error checking of cache contents, while IBM’s System z9 is one of the very few that provide parity checking on the cpu registers (“Enhanced I/O subsystem recovery and availability on the IBM System z9” by Oakes et al).
One solution to the problem of unreliable cpu behavior is for the compiler to insert consistency checks into the generated code. Two such checking methods are:
- ‘Signature Analysis’ which performs consistency checks between signatures calculated at compile time and runtime. A signature is associated with every basic block with the current signature being derived from the execution history. This technique can detect spurious changes to the flow of control caused by a hardware glitch.
- ‘Error Detection by Duplicated Instructions’ generates code which duplicates the behavior of some instruction sequence and compares the result calculated by both sequences, i.e., a source language construct is executed twice and an error raised if the results are different. The parallel instruction sequences use different sets of registers on the same cpu and ideally the instructions are scheduled to exploit instruction level parallelism
At the moment cosmic-ray induced hardware faults are probably very small change compared to faults in the code. Will code quality increase to the point where cosmic-ray faults become an issue or will devices get so small that they have to be lead lined to prevent background radiation corrupting them? Let the race begin.
Monte Carlo arithmetic operations
Working out whether software based calculations involving floating-point values delivers a sensible answer requires lots of mathematical sophistication and in practice is often impractical or intractable. The vast majority of developers make no effort, indeed most don’t even know why the effort is needed. Various ‘end-user’ solutions have been proposed, e.g., interval arithmetic.
One interesting solution is to perturb the result of floating-point operations and measure the effect on the final answer. Any calculation that is sensitive to small random changes in the result of an operation (there is randomness present in any operation that operates on values that can only be represented to a finite precision) will produce answers that depend on the direction and magnitude of the perturbation. Comparing the answers from several program executions provides a measure of one kind of error present in the calculation.
Monte Carlo arithmetic is a proposed extension of floating-point arithmetic that operates by randomly selecting how round-off errors occur (the proposer provides sample code).
With computing power continuing to increase, running a program several times is often a viable option (we don’t all number crunch for cpu days). Most of the transistors on a modern CPU chip are devoted to memory cache, using a few of these to support Monte Carlo arithmetic instructions is entirely practical. Perhaps when vendors get over supporting the base-10 radix required by the latest IEEE 754R standard and are looking for something new to attract customers they will provide a mechanism that makes it practical to obtain estimates of some of the error in floating-point calculations.
Recent Comments