Archive
Confidence intervals: my one recommended practice
What recommended practices should developers/managers follow when analysing data they have collected/available?
The scientific approach to data analysis mandates specifying a hypothesis before gathering the data, let alone analysing it. This approach has proven workable when researchers are familiar with an evidence-based body of knowledge. In this environment it’s acceptable, even required, to criticise anyone who analyses data without having a hypothesis and just follow along where ever the data appears to lead.
In fields lacking an evidence-based body of knowledge, such as software engineering (which does have an extensive body of folklore), it can be difficult to articulate a reasonable set of hypothesis to test against, before analysing the date. Time and cost are the incentives that push developers/managers in to simply following the data where ever it leads them:
- understandably, they are only interested in solving their own local problem, not building global theories of software engineering practices,
- as occasional data analysts, developers/managers probably have little or no experience in formulating hypothesis, and don’t have the time to become familiar with the existing evidence around the processes of interest,
- formulating a hypothesis, along with its associated model of the world, can require a surprising amount of work, often involving many interacting factors to consider (an ad-hoc approach based on an evolving analysis of data can appear to need a lot less effort).
Following the data can feel like the agile approach to data analysis. However, thoughtlessly following the data is fraught with dangers, particularly with small sample sizes (while there are often copious quantities of source, the human side of software engineering often involves miniscule sample sizes). It has always been difficult to get developers to slow down and think when writing code, it seems unrealistic to expect habits to change for data analysis.
I take a somewhat schizophrenic approach in my workshop for software developers, with many slides illustrating the dangers of just jumping in, along with other slides showing how to quickly find patterns in data (the main topic of conversation during the hands-on sessions).
My one recommended practice is that confidence intervals be calculated and included in the presented results. Why just one recommendation? I think recommendations involving sample size, hypothesis, thinking hard, etc will be ignored. Results showing wide confidence intervals highlight a range of possible problems: insufficient sample sizes, along with marginal effects and other uncertainties.
The scientific recommendation approach would be to use p-values. The problem with these is that they will probably have to be explained to developers/managers, who will have little idea about how to interpret them.
The presence of confidence intervals in a summary of results is a major step up from current practices. My experiences with developer/manager driven data analysis include:
- using data, that happens to be available, that has no connection to the questions of interest,
- collecting data, but fail to extract much information (because primitive analysis techniques were used). This situation is also very common in software engineering research papers,
- selling an idea, not the results, sometimes blatantly going against the direction implied by the data analysis (not so common in research papers),
- getting lucky/unlucky with subject performance, in a tiny sample, and claim certainty in the results.
Over/under estimation factor for ‘most estimates’
When asked to estimate the time taken to perform a software development related task, people regularly over or under estimate. What range of over/under estimation falls within the bounds of the term ‘most estimates’, i.e., the upper/lower bounds of the ratio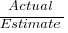 
(an overestimate occurs when 
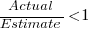, an underestimate when 
)?
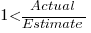On Twitter, I have been citing a factor of two for over/under time estimates. This factor of two involves some assumptions and a personal interpretation.
The following analysis is based on the two major software task effort estimation datasets: SiP and CESAW. The tasks in both datasets are for internal projects (i.e., no tendering against competitors), and require at most a few hours work.
The following analysis is based on the SiP data.
Of the 8,252 unique tasks in the SiP data, 30% are underestimates, 37% exact, and 33% overestimates.
How do we go about calculating bounds for the over/under factor of most estimates (a previous post discussed calculating an accuracy metric over all estimates)?
A simplistic approach is to average over each of the overestimated and underestimated tasks. The plot below shows hours estimated against the ratio actual/estimated, for each task (code+data):
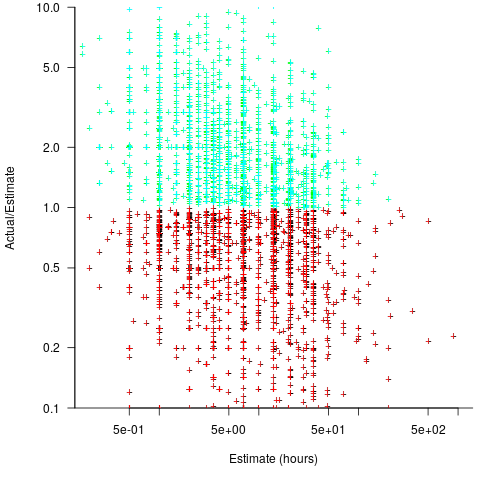
Averaging the over/under estimated tasks separately (using the geometric mean) gives 0.47 and 1.9 respectively, i.e., tasks are over/under estimated by a factor of two.
This approach fails to take into account the number of estimates that are over/under/equal, i.e., it ignores likelihood information.
A regression model takes into account the distribution of values, and we could adopt the fitted model’s prediction interval as the over/under confidence intervals. The prediction interval is the interval within which other observations are expected to fall, with some probability (R’s predict function uses one standard deviation).
The plot below shows a fitted regression model and prediction intervals at one standard deviation (68.3%) and two standard deviations (95%); the faint grey line shows Estimate == Actual (code+data):
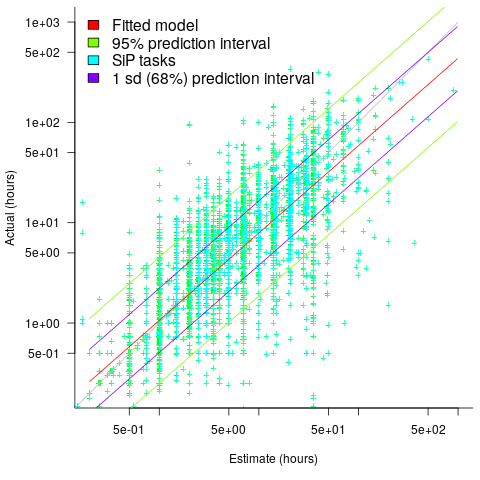
The fitted model tilts down from the upward direction of the Estimate == Actual line, consequently the over/under estimation factor depends on the size of the estimate. The table below lists the over/under estimation factor for low/high estimates at one & two standard deviations (68.3 and 95% probability).
People like simple answers (i.e., single values) and the mean value is a commonly used technique of summarising many values. The task estimate values are unevenly distributed and weighting the mean by the distribution of estimated values is more representative than, say, an evenly distributed set of estimates. The 5th and 6th columns in the table below list the weighted means at one/two standard deviations (the CESAW columns are the values for all projects in the CESAW data).
1 sd 2 sd Weighted mean CESAW
Low High Low High 1 sd 2 sd 1 sd 2 sd
Over 0.56 0.24 0.27 0.11 0.46 0.25 0.29 0.1
Under 2.4 1.0 4.9 2.0 2.00 4.1 2.4 6.5 |
The weighted means for over/under estimates are close to a factor of two of the actual (divide/multiply) within one standard deviation (68.3%), and a factor of four within two standard deviations (95%).
Why choose to give the one standard deviation factor, rather than the two? People talk of “most estimates”, but what percentage range does ‘most’ map to? I have tended to think of ‘most’ as more than two-thirds, e.g., at least one standard deviation (a recent study suggests that ‘most’ usage peaks at 80-85%), and I think of two standard deviations as ‘nearly all’ (i.e., 95%; there are probably people who call this ‘most’).
Perhaps a between two and four is a more appropriate answer (particularly since the bounds are wider for the CESAW data). Suggestions welcome.
Regression line fitted to noisy data? Ask to see confidence intervals
A little knowledge can be a dangerous thing. For instance, knowing how to fit a regression line to a set of points, but not knowing how to figure out whether the fitted line makes any sense. Fitting a regression line is trivial, with most modern data analysis packages; it’s difficult to find data that any of them fail to fit to a straight line (even randomly selected points usually contain enough bias on one direction, to enable the fitting algorithm to converge).
Two techniques for checking the goodness-of-fit, of a regression line, are plotting confidence intervals and listing the p-value. The confidence interval approach is a great way to visualize the goodness-of-fit, with the added advantage of not needing any technical knowledge. The p-value approach is great for blinding people with science, and a necessary technicality when dealing with multidimensional data (unless you happen to have a Tardis).
In 2016, the Nationwide Mutual Insurance Company won the IEEE Computer Society/Software Engineering Institute Watts S. Humphrey Software Process Achievement (SPA) Award, and there is a technical report, which reads like an infomercial, on the benefits Nationwide achieved from using SEI’s software improvement process. Thanks to Edward Weller for the link.
Figure 6 of the informercial technical report caught my eye. The fitted regression line shows delivered productivity going up over time, but the data looks very noisy. How good a fit is that regression line?
Thanks to WebPlotDigitizer, I quickly extracted the data (I’m a regular user, and WebPlotDigitizer just keeps getting better).
Below is the data plotted to look like Figure 6, with the fitted regression line in pink (code+data). The original did not include tick marks on the axis. For the x-axis I assumed each point was at a fixed 2-month interval (matching the axis labels), and for the y-axis I picked the point just below the zero to measure length (so my measurements may be off by a constant multiplier close to one; multiplying values by a constant will not have any influence on calculating goodness-of-fit).
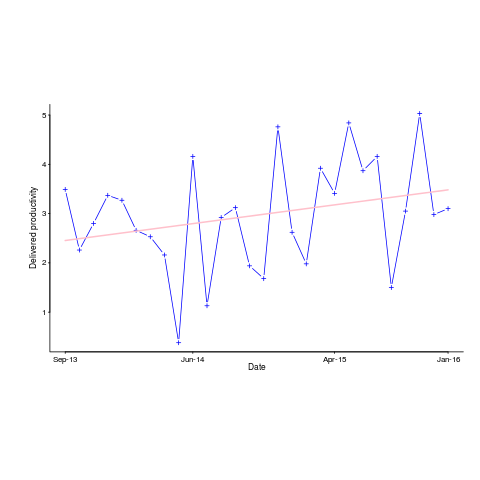
The p-value for the fitted line is 0.15; gee-wiz, you say. Plotting with confidence intervals (in red; the usual 95%) makes the situation clear:
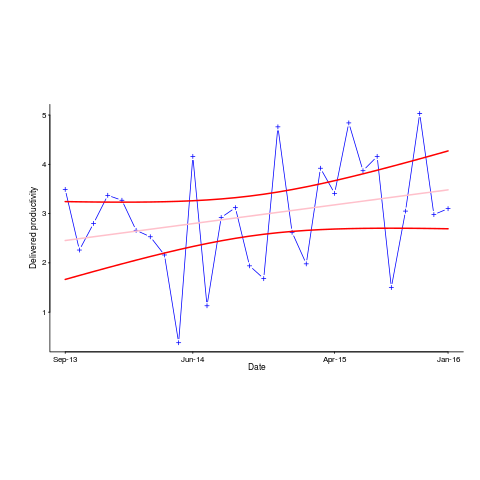
Ok, so the fitted model is fairly meaningless from a technical perspective; the line might actually go down, rather than up (there is too much noise in the data to tell). Think of the actual line likely appearing somewhere in the curved red tube.
Do Nationwide, IEEE or SEI care? The IEEE need a company to award the prize to, SEI want to promote their services, and Nationwide want to convince the rest of the world that their IT services are getting better.
Is there a company out there who feels hard done-by, because they did not receive the award? Perhaps there is, but are their numbers any better than Nationwide’s?
How much influence did the numbers in Figure 6 have on the award decision? Perhaps not a lot, the other plots look like they would tell a similar tail of wide confidence intervals on any fitted lines (readers might like to try their hand drawing confidence intervals for Figure 9). Perhaps Nationwide was the only company considered.
Who are the losers here? Other companies who decide to spend lots of money adopting the SEI software process? If evidence was available, perhaps something concrete could be figured out.
Recent Comments