Archive
A comparison of C++ and Rust compiler performance
Large code bases take a long time to compile and build. How much impact does the choice of programming language have on compiler/build times?
The small number of industrial strength compilers available for the widely used languages makes the discussion as much about distinct implementations as distinct languages. And then there is the issue of different versions of the same compiler having different performance characteristics; for instance, the performance of Microsoft’s C++ Visual Studio compiler depends on the release of the compiler and the version of the standard specified.
Implementation details can have a significant impact on compile time. Compile time may be dominated by lexical analysis, while support for lots of fancy optimization shifts the time costs to code generation, and poorly chosen algorithms can result in symbol table lookup being a time sink (especially for large programs). For short programs, compile time may be dominated by start-up costs. These days, developers rarely have to worry about small memory size causing occurring when compiling a large source file.
A recent blog post compared the compile/build time performance of Rust and C++ on Linux and Apple’s OS X, and strager kindly made the data available.
The most obvious problem with attempting to compare the performance of compilers for different languages is that the amount of code contained in programs implementing the same functionality will differ (this is also true when the programs are written in the same language).
strager’s solution was to take a C++ program containing 9.3k LOC, plus 7.3K LOC of tests, and convert everything to Rust (9.5K LOC, plus 7.6K LOC of tests). In total, the benchmark consisted of compiling/building three C++ source files and three equivalent Rust source files.
The performance impact of number of lines of source code was measured by taking the largest file and copy-pasting it 8, 16, and 32 times, to create three every larger versions.
The OS X benchmarks did not include multiple file sizes, and are not included in the following analysis.
A variety of toolchain options were included in different runs, and for Rust various command line options; most distinct benchmarks were run 10 times each. On Linux, there were a total of 360 C++ runs, and for Rust 1,066 runs (code+data).
The model 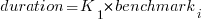 , where
, where 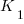 is a fitted regression constant, and
is a fitted regression constant, and 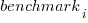 is the fitted regression coefficient for the
is the fitted regression coefficient for the 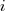 ‘th benchmark, explains just over 50% of the variance. The language is implicit in the benchmark information.
‘th benchmark, explains just over 50% of the variance. The language is implicit in the benchmark information.
The model 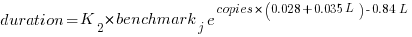 , where
, where 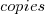 is the number of copies,
is the number of copies, 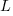 is 0 for C++ and 1 for Rust, explains 92% of the variance, i.e., it is a very good fit.
is 0 for C++ and 1 for Rust, explains 92% of the variance, i.e., it is a very good fit.
The expression 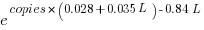 is a language and source code size multiplication factor. The numeric values are:
is a language and source code size multiplication factor. The numeric values are:
1 8 16 32 C++ 1.03 1.25 1.57 2.45 Rust 0.98 1.52 2.52 6.90 |
showing that while Rust compilation is faster than C++, for ‘shorter’ files, it becomes much relatively slower as the quantity of source increases.
The size factor for Rust is growing quadratically, while it is much closer to linear for C++.
What are the threats to the validity of this benchmark comparison?
The most obvious is the small number of files benchmarked. I don’t have any ideas for creating a larger sample.
How representative is the benchmark of typical projects? An explicit goal in benchmark selection was to minimise external dependencies (to reduce the effort likely to be needed to translate to Rust). Typically, projects contain many dependencies, with compilers sometimes spending more time processing dependency information than compiling the actual top-level source, e.g., header files in C++.
A less obvious threat is the fact that the benchmarks for each language were run in contiguous time intervals, i.e., all Rust, then all C++, then all Rust (see plot below; code+data):

It is possible that one or more background processes were running while one set of language benchmarks was being run, which would skew the results. One solution is to intermix the runs for each language (switching off all background tasks is much harder).
I was surprised by how well the regression model fitted the data; the fit is rarely this good. Perhaps a larger set of benchmarks would increase the variance.
Frequency of non-linear relationships in software engineering data
Causality is an integral part of the developer mindset, and correlation is a common hammer that developers use for the analysis of data (usually the Pearson correlation coefficient).
The problem with using Pearson correlation to analyse software engineering data is that it calculates a measure of linear relationships, and software data is often non-linear. Using a more powerful technique would not only enable any non-linearity to be handled, it would also extract more information, e.g., regression analysis.
My impression is that power laws and exponential relationships abound in software engineering data, but exactly how common are they (and let’s not forget polynomial relationships, e.g., quadratics)?
I claim that my Evidence-based Software Engineering analyses all the publicly available software engineering data. How often do non-linear relationships occur in this data?
The data is invariably plotted, and often a regression model is fitted. A search of the data analysis code (written in R) located 996 calls to plot and 446 calls to glm (used to fit a regression model; shell script).
In calls to plot, the log argument can be used to specify that a log-scale be used for a given axis. When the data has an exponential distribution, I specified the appropriate axis to be log-scaled (18% of cases); for a power law, both axis were log-scaled (11% of cases).
In calls to glm, one or more of the formula variables may be log transformed within the formula. When the data has an exponential distribution, either the left-hand side of the formula is log transformed (20% of cases), or one of the variables on the right-hand side (9% of cases, giving 29% in total); for a power law both sides of the formula are log transformed (12% of cases).
Within a glm formula, variables can be raised to a power by enclosing the expression in the I function (the ^ operator has a special meaning within a formula, but its usual meaning inside I). The most common operation appearing inside I is ^2, i.e., squaring a value. In the following table, only formula that did not log transform any variable were searched for calls to I.
The analysis code contained 54 calls to the nls function, whose purpose is to fit non-linear regression models.
plot log="x" log="y" log="xy"
996 4% 14% 11%
glm log(x) log(y) log(y) ~ log(x) I()
446 9% 20% 12% 12% |
Based on these figures (shell script), at least 50% of software engineering data contains non-linear relationships; the values in this table are a lower bound, because variables may have been transformed outside the call to plot or glm.
The at least 50% estimate is based on all software engineering, some corners will have higher/lower likelihood of encountering non-linear data; for instance, estimation data often contains power law relationships.
Coding mistakes made by ChatGTP
The programs generated by Openai‘s chat-bot ChatGPT, sometimes referred to as GPT-3, may have the requested behavior, but often contain mistakes that illustrate the fact that ChatGPT does not know anything about programming.
ChatGPT does not understand anything, it is a token prediction engine driven by the corpus used to train its language model. The likelihood of the output being correct is dependent on the quantity of text used during training (the more text used, the more likely that it will contain a relevant response). GTP-3, the language model behind ChatGPT, was trained on the deduplicated contents of the Internet (the language model has 175 billion parameters, the GTP-2 model contains 1.5 billion parameters). The practicality of its implementation is the result of various trade-offs, along with technical breakthroughs in language model building, e.g., transformers.
ChatGPT output appears to be that of a next generation search engine, one that returns answers rather than links to pages.
Readers who believe that any ‘understanding’ pixie dust is involved can disabuse themselves of this notion by reading an overview of GTP-3’s architecture, and how the transformer algorithm converts text to matrices of values.
If matrix algebra is not your thing, check out the 257 lines of python that nanoGTP uses for training, and the 75 lines used to generate responses from a trained model.
As a prediction engine, ChatGTP sometimes gets things wrong. What kind of mistakes appear in ChatGPT generated source code?
The exchanges below occurred with ChatGPT Jan 9 version, with the text typed by me appearing in bold, and the ChatGPT output appearing in the following boxed text.
Some of my questions were inspired by the list of undefined behaviors in the C Standard.
Write a program that adds apples to oranges.
I'm sorry, I don't understand what you mean by "adding apples to oranges." Can you please provide more information or context? |
A suitable response can only be provided when an appropriate match is found in the trained model.
Write a regular expression that matches all prime numbers.
It is not possible to write a regular expression that can match all prime numbers, as the set of prime numbers is infinite and a regular expression is a finite representation of a pattern. Additionally, regular expressions are used to match strings of characters, while prime numbers are numerical values. It is possible to use a regex to match a number in a string but it's not capable of determining if the number is prime or not. |
The training data may include the information that the request cannot be met.
Write a regular expression that matches all even numbers.
A regular expression that matches all even numbers is:
^(0|[2468]*[048]|[13579][26])$
Explanation:
^ matches the start of the string
(0|[2468]*[048]|[13579][26]) matches any of the following:
0
any number of even digits followed by a 0 or 8 (for example, 200, 2468000)
any odd digit followed by a 6 (for example, 1357926)
$ matches the end of the string
This regular expression will match strings that contain only even numbers, but not those that contain other characters. |
The generated regular expression does not do what I asked, or what the last sentence from ChatGTP claims.
What is going on?
The tokens “Write a regular expression that matches” were enough for ChatGTP to figure out the task.
The tokens “all even numbers” was not specific enough for ChatGTP to focus on the appropriate training data. There is a random component to the selection of output, which will play a larger role when there are many possibilities.
The method used to tokenized/encode character sequences during training (i.e., byte-pairs), along with the relatively limited number of distinct tokens (i.e., 50,257) means that only one-/two-digit numbers are likely to be represented as discrete entities; longer digit sequences are treated as co-occurrences of one-/two-digit tokens. So it is not a surprise to see ChatGPT applying co-occurrences characteristics of long digit sequences to its component subsequences.
Write a regular expression that matches all odd numbers.
A regular expression that matches all odd numbers is:
^(1|[13579]*[13579])$
Explanation:
^ matches the start of the string
(1|[13579]*[13579]) matches any of the following:
1
any number of odd digits followed by another odd digit (for example, 1357913579)
$ matches the end of the string
This regular expression will match strings that contain only odd numbers, but not those that contain other characters. |
The output for odd numbers is more consistent, in that the regular expression does what the last sentence of the output claims, but not what I asked.
During a chat session, it is possible to provide more (information in human terminology; character sequences in ChatGTP terminology). The following prompt text, from me, has nothing to do with teaching ChatGTP to do maths, but providing tokens that enable a more focused match against training data.
Even numbers are defined as divisible by two with no reminder. If a number is not even then it is odd.
You are correct, even numbers are defined as divisible by two with no remainder, and if a number is not even, it is considered odd. I apologize for any confusion caused by my previous statement. To match all even numbers, we can use the regular expression: ^([0-9]*[02468])$ To match all odd numbers, we can use the regular expression: ^([0-9]*[13579])$ Both of this regular expression will match numbers that are divisible by 2 and not divisible by 2 respectively. |
Both generated regular expressions are correct.
ChatGPT can learn to translate from an invented language to English (and presumably other languages).
Give an example of C source code assigning a character constant that contains an invalid multibyte character.
The following is an example of C source code assigning a character constant that contains an invalid multibyte character:
#include <stdio.h>
int main() {
char invalid_char = '\xF0\x90\x80\x80'; // This is an invalid multibyte character
printf("%c", invalid_char);
return 0;
}
In this example, the character constant '\xF0\x90\x80\x80' is assigned to the variable invalid_char. This particular sequence of bytes is not a valid Unicode character, and it will produce undefined behavior when attempting to print it. |
There was a time when '\xF0\x90\x80\x80' was an invalid multibyte character.
Things changed around 20 years ago, but the training for the model used by ChatGTP does not tag information with valid-between dates.
ChatGTP searches for, and finds, an invalid multibyte character, and uses it to provide an answer.
Give an example of C source code where an object is referred to outside of its lifetime.
The following is an example of C source code where an object is referred to outside of its lifetime:
#include <stdio.h>
int main() {
int x;
{
int x = 5;
}
printf("x: %d\n", x);
return 0;
}
In this example, the variable x is defined twice in the same function main. The first definition int x; is a global variable that has a lifetime throughout the entire program execution. The second definition int x = 5; is a local variable that has a lifetime that is limited to the inner block {...} it is defined in.
After the inner block is executed and the inner variable x goes out of scope, the program attempts to access the inner variable x by using the global variable x in the printf statement, which refers to an object (the inner variable x) that is no longer in its lifetime. This behavior is undefined according to the C standard and can lead to unexpected results. |
The generated code is incorrect. The human interpretation of this code is that ChatGTP has confused the name of an object (what the C Standard calls a variable) and the storage it represents. There are two different objects defined, both having the name x (beginners often make the same mistake).
A common example of the requested behavior is freeing the dynamic storage pointed to by some pointer, and then accessing that storage.
Write a C program containing a conversion of an integer type that produces a value outside the range that can be represented in the integer type.
Here is an example of a C program that demonstrates the conversion of an integer type that produces a value outside the range that can be represented in the integer type:
#include <stdio.h>
int main() {
int x = 2147483647; // largest value representable in a signed 32-bit integer
unsigned int y = (unsigned int) x + 1; // overflow occurs here
printf("%u\n", y);
return 0;
}
In this program, the value of x is initialized to the largest value that can be represented by a signed 32-bit integer (2147483647). Then, x is cast to an unsigned 32-bit integer and 1 is added to it. Since the result of this operation is larger than the largest representable value in an unsigned 32-bit integer, an overflow occurs and the value of y becomes 0.
This program will produce an output of 0.
It is worth mentioning that undefined behavior (UB) can occur when an integer overflow happens, so this should be avoided in production code. |
The detailed explanation makes the output look like its authoritative. However, it is wrong.
There is no overflow in this code.
The integer type ‘unsigned int’ supports a larger range of positive values, which means that after conversion, adding one will not produce a value that is outside the range that can be represented.
You are correct, I apologize for the confusion. Unsigned integers have a larger range of positive values and do not have negative values. When an operation like an addition exceeds the maximum value that can be represented by an unsigned integer, it wraps around to the minimum value representable by that type, which is typically zero, instead of an overflow.
For example, if you use an unsigned int and the maximum value it can represent is 4,294,967,295, if you add 1 to that value, it will wrap around to 0.
Here is an example of a C program that demonstrates the conversion of an integer type that produces a value outside the range that can be represented in the integer type:
#include <stdio.h>
int main() {
int x = -2147483648; // lowest value representable in a signed 32-bit integer
unsigned int y = (unsigned int) x -1; // wrap around occurs here
printf("%u\n", y);
return 0;
}
In this program, the value of x is initialized to the lowest value that can be represented by a signed 32-bit integer (-2147483648) which is lower than 0. Then, x is cast to an unsigned 32-bit integer and 1 is subtracted from it. Since the result of this operation is lower than 0, the value wraps around to the maximum representable value in an unsigned 32-bit integer (4,294,967,295) . This program will produce an output of 4,294,967,295.
It is worth mentioning that this wrapping around behavior is defined for unsigned integers in C and C++, but it is not always the case in other programming languages. |
This output contained the requested behavior, although subtracting one is unnecessary code.
ChatGTP can also be used to create documentation 😉
Write a poem in Iambic pentameter about the benefit of an evidence based approach to software engineering in the style of a party political broadcast.
With evidence-based approach, our work shall shine, For in software engineering, it's the only way to dine. We'll test and measure, as we go along, To make our code robust, and errors gone. Our methodologies, backed by data and proof, Will bring success and progress, that's the truth. We'll avoid the pitfalls, of guesses and guesses, And build systems, that pass all tests. We'll listen to the data, and the users' voice, To make our software, the best by choice. We'll iterate and improve, with every release, And build a product, that truly will please. So join us now, and embrace the way, Of evidence-based approach, for brighter day. With data and research, we'll conquer all, In software engineering, we'll never fall. |
Evaluating Story point estimation error
If a task implementation estimate is expressed in time, various formula are available for evaluating how well the estimated time corresponds to the actual time.
When an estimate is expressed in story points, how might the estimate be evaluated when actual time is measured in hours?
The common practice of selecting story point values from a small set of integers (I have seen fractional values used) introduces quantization error into most estimates (around 30% of time estimates equal actual time), assuming that actual times are not constrained to a similar number of possible time values.
If we assume a linear mapping from estimated story points to actual time and an ideal estimator (let’s assume that 1 story point is equivalent to 1 hour), then a lower bound on the error can be calculated.
Our ideal estimator is able to exactly predict the actual time. However, the use of story points means that this exact prediction has to be rounded to one of a small set of integer values. Let’s assume that our ideal estimator rounds to the story point value that is closest to the exact prediction, e.g., all story points predicted to take up to 1.5 are estimated at 1 story point.
What is the mean error of the estimates made by this ideal, rounded, estimator?
The available evidence shows that the distribution of tasks having a given actual implementation time roughly has the form of a geometric (the discrete form of exponential) or negative binomial distribution. The plot below shows a geometric and negative binomial distribution, with distinct colors over the range where values are rounded to the same closest integer (dots are at 1-minute intervals, code):
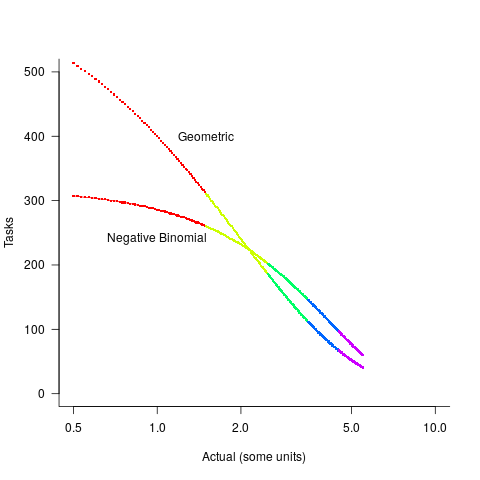
Having picked a distribution for actual times, we can calculate the number of tasks estimated to require, for instance, 1 story point, but actually taking 1 hour, 1 hr 1 min, 1 hr 2 min, …, 1 hr 30 min. The mean error can be calculated over each pair of estimate/actual, for one to five story points (in this example). The table below lists the mean error for two actual distributions, calculated using four common metrics: squared error (SE), absolute error (AE), absolute percentage error (APE), and relative error (RE); code:
Distribution SE AE APE RE Geometric 0.087 0.26 0.17 0.20 Negative Binomial 0.086 0.25 0.14 0.16 |
A few minutes difference in a 1 SP estimate is a larger error than the same number of minutes in a two or more SP estimate, combined with most tasks take a small amount of time, means that error estimation is dominated by inaccuracies in estimating small tasks.
In practice, the range of actual times, for a given estimate, is better approximated by a percentage of the estimated time (50% is used below), and the number of tasks having a given actual value for a given estimate, approximated by a triangular distribution (a cubic equation was used for the following calculation). The plot below shows the distribution of estimation points around a given number of story points (at 1-minute intervals), and the geometric and negative binomial distribution (compare against plot above to work out which is which; code):
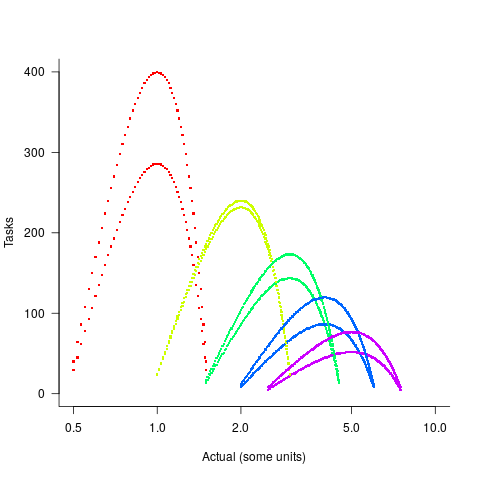
The following table lists of mean errors:
Distribution SE AE APE RE Geometric 0.52 0.55 0.13 0.13 Negative Binomial 0.62 0.61 0.13 0.14 |
When the error in the actual is a percentage of the estimate, larger estimates have a much larger impact on absolute accuracy; see the much larger SE and AE values. The impact on the relative accuracy metrics appears to be small.
Is evaluating estimation error useful, when estimates are given in story points?
While it’s possible to argue for and against, the answer is that usefulness is in the eye of the beholder. If development teams find the information useful, then it is useful; otherwise not.
Focus of activities planned for 2023
In 2023, my approach to evidence-based software engineering pivots away from past years, which were about maximizing the amount of software engineering data gathered.
I plan to spend a lot more time attempting to join dots (i.e., finding useful patterns in the available data), and I also plan to spend time collecting my own data (rather than other peoples’ data).
I will continue to keep asking people for data, and I’m sure that new data will become available (and be the subject of blog posts). The amount of previously unseen data obtained by continuing to read pre-2020 papers is likely to be very small, and not worth targetting. Post-2020 papers will be the focus of my search for new data (mostly conference proceedings and arXiv’s software engineering recent submissions)
It would be great if there was an active community of evidence-based developers. The problem is that the people with the necessary skills are busily employed building real systems. I’m hopeful that people with the appropriate background and skills will come out of the woodwork.
Ideally, I would be running experiments with developer subjects; this is the only reliable way to verify theories of software engineering. While it’s possible to run small scale experiments with developer volunteers, running a workplace scale experiment will be expensive (several million pounds/dollars). I don’t move in the circles frequented by the very wealthy individuals who might fund such an experiment. So this is a back-burner project.
if-statements continue to be of great interest to me; they represent decisions that relate to requirements and tests that need to be written. I used to spend a lot of time measuring, mostly C, source code: how the same variable is tested in nested conditions, the use of else arms, and the structuring of conditions within a function. The availability of semgrep will, hopefully, enable me to measure various aspect of if-statement usage across different languages.
I hope that my readers continue to keep their eyes open for interesting software engineering data, and will let me know when they find any.
Recent Comments