Archive
Rounding and heaping in non-software estimates
Round numbers are often preferred in software task estimation times, e.g., 1, 5, 7 (hours in one working day), and 14. This human preference for round numbers is not specific to software, or to estimating. Round numbers can act as goals, as clustering points, may be used more often as uncertainty increases, or be the result of satisficing, etc.
Rounding can occur in response to any question involving a numeric value, e.g., a government census or survey asking citizens about their financial situation or health. Rounding introduces error in the analysis of data. The Whipple index, described in 1919, was the first attempt to quantify the amount of error; calculated as: “per cent which the number reported as multiples of 5 forms of one-fifth of the total number between ages 23 to 62 years inclusive.” for errors of reported age. Other metrics for this error have been proposed, and packages to calculate them are available.
At some point (the evidence suggests a 1940 paper) a published paper introduced the term heaping effect. These days, heaping is more often used to name the process, compared to rounding, e.g., heaping of values; ‘heaping’ papers do use the term rounding, but I have not seen ’rounding’ papers use heaping.
The choice of rounding values depends on the unit of measurement. For instance, reported travel arrival/departure times are rounded to intervals of 5, 14, 30 and 60 minutes; based on reported/actual travel times it is possible to estimate the probability that particular rounding intervals have been used.
The Whipple index fails when all the values are large (e.g., multiple thousands), or take a small range of values (e.g., between one and twenty).
One technique for handling rounding of large values is to define roundedness in terms of the fraction of value digits that are trailing zeroes. The plot below shows the number of households having a given estimated balance on their first mortgage in the 2013 Survey of Consumer Finances (in red), and the distribution of actual balances reported by the New York Federal Reserve (in blue/green; data extracted from plot in a paper and scaled to equalize total mortgage values; code+data):
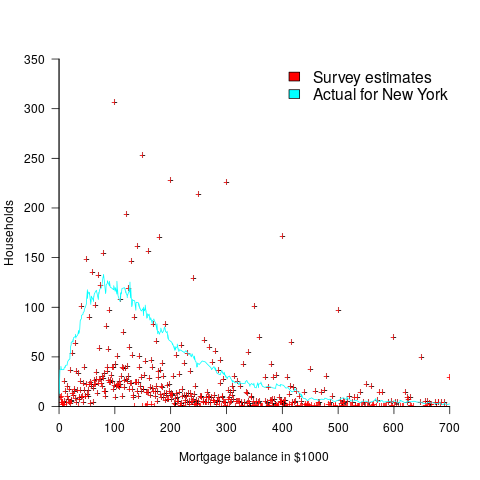
The relatively high number of distinct round numbers swamps any underlying distribution of actual values. While some values having some degree of roundness occur more often than non-round values, they still appear less often than expected by the known distribution. It is possible that homeowners have mortgages at round values because they of banking limits, or reasons other than rounding when answering the survey.
The plot below shows the number of people reporting having a given number of friends, plus number of cigarettes smoked per day, from the 2015 survey of Objective and Subjective Quality of Life in Poland (code+data):
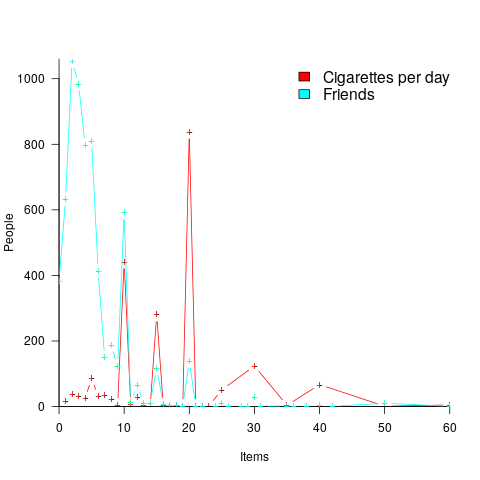
The narrow range of a person’s number of friends prevents the Whipple index from effectively detecting rounding/heaping.
The dominance of round numbers in the cigarettes smoked per day may be caused by the number of cigarettes contained in a packet, i.e., people may be accurately reporting that they smoke the contents of a packet, rather than estimating a rounded number.
Simple techniques are available for correcting the mean/variance when values are always rounded to specified boundaries. When the probability of rounding is not 100%, the calculation is more complicated.
Rounded/Heaped data contains multiple distributions, i.e., the non-rounded values and the rounded values; various mixture models have been proposed to fit such data. Alternatively, the data can be ‘deheaped’, and various deheaping techniques have been proposed.
Given the prevalence of significant amounts of rounding/heaping, it’s surprising how few people know about it.
Complex software makes economic sense
Economic incentives motivate complexity as the common case for software systems.
When building or maintaining existing software, often the quickest/cheapest approach is to focus on the features/functionality being added, ignoring the existing code as much as possible. Yes, the new code may have some impact on the behavior of the existing code, and as new features/functionality are added it becomes harder and harder to predict the impact of the new code on the behavior of the existing code; in particular, is the existing behavior unchanged.
Software is said to have an attribute known as complexity; what is complexity? Many definitions have been proposed, and it’s not unusual for people to use multiple definitions in a discussion. The widely used measures of software complexity all involve counting various attributes of the source code contained within individual functions/methods (e.g., McCabe cyclomatic complexity, and Halstead); they are all highly correlated with lines of code. For the purpose of this post, the technical details of a definition are glossed over.
Complexity is often given as the reason that software is difficult to understand; difficult in the sense that lots of effort is required to figure out what is going on. Other causes of complexity, such as the domain problem being solved, or the design of the system, usually go unmentioned.
The fact that complexity, as a cause of requiring more effort to understand, has economic benefits is rarely mentioned, e.g., the effort needed to actively use a codebase is a barrier to entry which allows those already familiar with the code to charge higher prices or increases the demand for training courses.
One technique for reducing the complexity of a system is to redesign/rework its implementation, from a system/major component perspective; known as refactoring in the software world.
What benefit is expected to be obtained by investing in refactoring? The expected benefit of investing in redesign/rework is that a reduction in the complexity of a system will reduce the subsequent costs incurred, when adding new features/functionality.
What conditions need to be met to make it worthwhile making an investment,  , to reduce the complexity,
, to reduce the complexity, 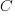 , of a software system?
, of a software system?
Let’s assume that complexity increases the cost of adding a feature by some multiple (greater than one). The total cost of adding  features is:
features is:
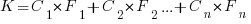
where: 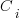 is the system complexity when feature
is the system complexity when feature 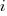 is added, and
is added, and 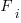 is the cost of adding this feature if no complexity is present.
is the cost of adding this feature if no complexity is present.
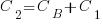 ,
, 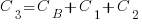 , …
, … 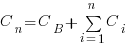
where: 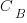 is the base complexity before adding any new features.
is the base complexity before adding any new features.
Let’s assume that an investment,  , is made to reduce the complexity from
, is made to reduce the complexity from 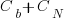 (with
(with 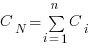 ) to
) to 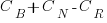 , where
, where 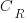 is the reduction in the complexity achieved. The minimum condition for this investment to be worthwhile is that:
is the reduction in the complexity achieved. The minimum condition for this investment to be worthwhile is that:
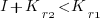 or
or 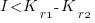
where: 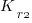 is the total cost of adding new features to the source code after the investment, and
is the total cost of adding new features to the source code after the investment, and 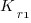 is the total cost of adding the same new features to the source code as it existed immediately prior to the investment.
is the total cost of adding the same new features to the source code as it existed immediately prior to the investment.
Resetting the feature count back to 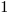 , we have:
, we have:
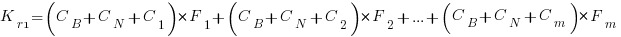
and
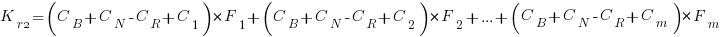
and the above condition becomes:
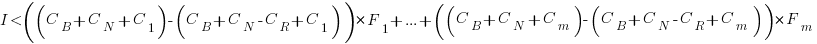
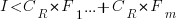
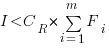
The decision on whether to invest in refactoring boils down to estimating the reduction in complexity likely to be achieved (as measured by effort), and the expected cost of future additions to the system.
Software systems eventually stop being used. If it looks like the software will continue to be used for years to come (software that is actively used will have users who want new features), it may be cost-effective to refactor the code to returning it to a less complex state; rinse and repeat for as long as it appears cost-effective.
Investing in software that is unlikely to be modified again is a waste of money (unless the code is intended to be admired in a book or course notes).
A new career in software development: advice for non-youngsters
Lately I have been encountering non-young people looking to switch careers, into software development. My suggestions have centered around the ageism culture and how they can take advantage of fashions in software ecosystems to improve their job prospects.
I start by telling them the good news: the demand for software developers outstrips supply, followed by the bad news that software development culture is ageist.
One consequence of the preponderance of the young is that people are heavily influenced by fads and fashions, which come and go over less than a decade.
The perception of technology progresses through the stages of fashionable, established and legacy (management-speak for unfashionable).
Non-youngsters can leverage the influence of fashion’s impact on job applicants by focusing on what is unfashionable, the more unfashionable the less likely that youngsters will apply, e.g., maintaining Cobol and Fortran code (both seriously unfashionable).
The benefits of applying to work with unfashionable technology include more than a smaller job applicant pool:
- new technology (fashion is about the new) often experiences a period of rapid change, and keeping up with change requires time and effort. Does somebody with a family, or outside interests, really want to spend time keeping up with constant change at work? I suspect not,
- systems depending on unfashionable technology have been around long enough to prove their worth, the sunk cost has been paid, and they will continue to be used until something a lot more cost-effective turns up, i.e., there is more job security compared to systems based on fashionable technology that has yet to prove their worth.
There is lots of unfashionable software technology out there. Software can be considered unfashionable simply because of the language in which it is written; some of the more well known of such languages include: Fortran, Cobol, Pascal, and Basic (in a multitude of forms), with less well known languages including, MUMPS, and almost any mainframe related language.
Unless you want to be competing for a job with hordes of keen/cheaper youngsters, don’t touch Rust, Go, or anything being touted as the latest language.
Databases also have a fashion status. The unfashionable include: dBase, Clarion, and a whole host of 4GL systems.
Be careful with any database that is NoSQL related, it may be fashionable or an established product being marketed using the latest buzzwords.
Testing and QA have always been very unsexy areas to work in. These areas provide the opportunity for the mature applicants to shine by highlighting their stability and reliability; what company would want to entrust some young kid with deciding whether the software is ready to be released to paying customers?
More suggestions for non-young people looking to get into software development welcome.
Evaluating estimation performance
What is the best way to evaluate the accuracy of an estimation technique, given that the actual values are known?
Estimates are often given as point values, and accuracy scoring functions (for a sequence of estimates) have the form 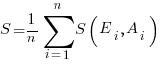 , where
, where  is the number of estimated values,
is the number of estimated values, 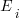 the estimates, and
the estimates, and 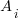 the actual values; smaller
the actual values; smaller 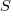 is better.
is better.
Commonly used scoring functions include:
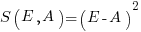 , known as squared error (SE)
, known as squared error (SE)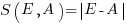 , known as absolute error (AE)
, known as absolute error (AE)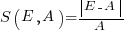 , known as absolute percentage error (APE)
, known as absolute percentage error (APE)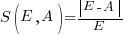 , known as relative error (RE)
, known as relative error (RE)
APE and RE are special cases of: 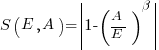 , with
, with 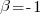 and
and 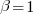 respectively.
respectively.
Let’s compare three techniques for estimating the time needed to implement some tasks, using these four functions.
Assume that the mean time taken to implement previous project tasks is known, 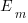 . When asked to implement a new task, an optimist might estimate 20% lower than the mean,
. When asked to implement a new task, an optimist might estimate 20% lower than the mean, 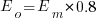 , while a pessimist might estimate 20% higher than the mean,
, while a pessimist might estimate 20% higher than the mean, 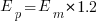 . Data shows that the distribution of the number of tasks taking a given amount of time to implement is skewed, looking something like one of the lines in the plot below (code):
. Data shows that the distribution of the number of tasks taking a given amount of time to implement is skewed, looking something like one of the lines in the plot below (code):
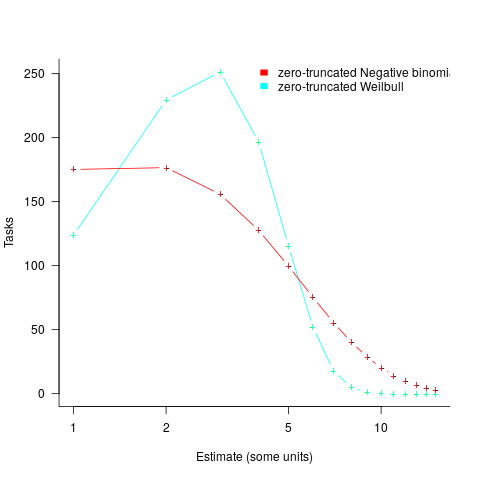
We can simulate task implementation time by randomly drawing values from a distribution having this shape, e.g., zero-truncated Negative binomial or zero-truncated Weibull. The values of 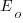 and
and 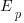 are calculated from the mean,
are calculated from the mean, 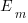 , of the distribution used (see code for details). Below is each estimator’s score for each of the scoring functions (the best performing estimator for each scoring function in bold; 10,000 values were used to reduce small sample effects):
, of the distribution used (see code for details). Below is each estimator’s score for each of the scoring functions (the best performing estimator for each scoring function in bold; 10,000 values were used to reduce small sample effects):
SE AE APE RE
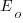 2.73 1.29 0.51 0.56
2.73 1.29 0.51 0.56
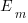 2.31 1.23 0.39 0.68
2.31 1.23 0.39 0.68
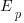 2.70 1.37 0.36 0.86
2.70 1.37 0.36 0.86
Surprisingly, the identity of the best performing estimator (i.e., optimist, mean, or pessimist) depends on the scoring function used. What is going on?
The analysis of scoring functions is very new. A 2010 paper by Gneiting showed that it does not make sense to select the scoring function after the estimates have been made (he uses the term forecasts). The scoring function needs to be known in advance, to allow an estimator to tune their responses to minimise the value that will be calculated to evaluate performance.
The mathematics involves Bregman functions (new to me), which provide a measure of distance between two points, where the points are interpreted as probability distributions.
Which, if any, of these scoring functions should be used to evaluate the accuracy of software estimates?
In software estimation, perhaps the two most commonly used scoring functions are APE and RE. If management selects one or the other as the scoring function to rate developer estimation performance, what estimation technique should employees use to deliver the best performance?
Assuming that information is available on the actual time taken to implement previous project tasks, then we can work out the distribution of actual times. Assuming this distribution does not change, we can calculate APE and RE for various estimation techniques; picking the technique that produces the lowest score.
Let’s assume that the distribution of actual times is zero-truncated Negative binomial in one project and zero-truncated Weibull in another (purely for convenience of analysis, reality is likely to be more complicated). Management has chosen either APE or RE as the scoring function, and it is now up to team members to decide the estimation technique they are going to use, with the aim of optimising their estimation performance evaluation.
A developer seeking to minimise the effort invested in estimating could specify the same value for every estimate. Knowing the scoring function (top row) and the distribution of actual implementation times (first column), the minimum effort developer would always give the estimate that is a multiple of the known mean actual times using the multiplier value listed:
APE RE
Negative binomial 1.4 0.5
Weibull 1.2 0.6
For instance, management specifies APE, and previous task/actuals has a Weibull distribution, then always estimate the value 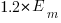 .
.
What mean multiplier should Esta Pert, an expert estimator aim for? Esta’s estimates can be modelled by the equation 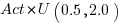 , i.e., the actual implementation time multiplied by a random value uniformly distributed between 0.5 and 2.0, i.e., Esta is an unbiased estimator. Esta’s table of multipliers is:
, i.e., the actual implementation time multiplied by a random value uniformly distributed between 0.5 and 2.0, i.e., Esta is an unbiased estimator. Esta’s table of multipliers is:
APE RE
Negative binomial 1.0 0.7
Weibull 1.0 0.7
A company wanting to win contracts by underbidding the competition could evaluate Esta’s performance using the RE scoring function (to motivate her to estimate low), or they could use APE and multiply her answers by some fraction.
In many cases, developers are biased estimators, i.e., individuals consistently either under or over estimate. How does an implicit bias (i.e., something a person does unconsciously) change the multiplier they should consciously aim for (having analysed their own performance to learn their personal percentage bias)?
The following table shows the impact of particular under and over estimate factors on multipliers:
0.8 underestimate bias 1.2 overestimate bias
Score function APE RE APE RE
Negative binomial 1.3 0.9 0.8 0.6
Weibull 1.3 0.9 0.8 0.6
Let’s say that one-third of those on a team underestimate, one-third overestimate, and the rest show no bias. What scoring function should a company use to motivate the best overall team performance?
The following table shows that neither of the scoring functions motivate team members to aim for the actual value when the distribution is Negative binomial:
APE RE
Negative binomial 1.1 0.7
Weibull 1.0 0.7
One solution is to create a bespoke scoring function for this case. Both APE and RE are special cases of a more general scoring function (see top). Setting 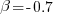 in this general form creates a scoring function that produces a multiplication factor of 1 for the Negative binomial case.
in this general form creates a scoring function that produces a multiplication factor of 1 for the Negative binomial case.
Twitter and evidence-based software engineering
This year’s quest for software engineering data has led me to sign up to Twitter (all the software people I know, or know-of, have been contacted, and discovery through articles found on the Internet is a very slow process).
@evidenceSE is my Twitter handle. If you get into a discussion and want some evidence-based input, feel free to get me involved. Be warned that the most likely response, to many kinds of questions, is that there is no data.
My main reason for joining is to try and obtain software engineering data. Other reasons include trying to introduce an evidence-based approach to software engineering discussions and finding new (to me) problems that people want answers to (that are capable of being answered by analysing data).
The approach I’m taking is to find software engineering tweets discussing a topic for which some data is available, and to jump in with a response relating to this data. Appropriate tweets are found using the search pattern: (agile OR software OR "story points" OR "story point" OR "function points") (estimate OR estimates OR estimating OR estimation OR estimated OR #noestimates OR "evidence based" OR empirical OR evolution OR ecosystems OR cognitive). Suggestions for other keywords or patterns welcome.
My experience is that the only effective way to interact with developers is via meaningful discussion, i.e., cold-calling with a tweet is likely to be unproductive. Also, people with data often don’t think that anybody else would be interested in it, they have to convinced that it can provide valuable insight.
You never know who has data to share. At a minimum, I aim to have a brief tweet discussion with everybody on Twitter involved in software engineering. At a minute per tweet (when I get a lot more proficient than I am now, and have workable templates in place), I could spend two hours per day to reach 100 people, which is 35,000 per year; say 20K by the end of this year. Over the last three days I have managed around 10 per day, and obviously need to improve a lot.
How many developers are on Twitter? Waving arms wildly, say 50 million developers and 1 in 1,000 have a Twitter account, giving 50K developers (of which an unknown percentage are active). A lower bound estimate is the number of followers of popular software related Twitter accounts: CompSciFact has 238K, Unix tool tips has 87K; perhaps 1 in 200 developers have a Twitter account, or some developers have multiple accounts, or there are lots of bots out there.
I need some tools to improve the search process and help track progress and responses. Twitter has an API and a developer program. No need to worry about them blocking me or taking over my business; my usage is small fry and I’ not building a business to take over. I was at Twitter’s London developer meetup in the week (the first in-person event since Covid) and the youngsters present looked a lot younger than usual. I suspect this is because the slightly older youngsters remember how Twitter cut developers off at the knee a few years ago by shutting down some useful API services.
The Twitter version-2 API looks interesting, and the Twitter developer evangelists are keen to attract developers (having ‘wiped out’ many existing API users), and I’m happy to jump in. A Twitter API sandbox for trying things out, and there are lots of example projects on Github. Pointers to interesting tools welcome.
Recent Comments