Archive
Transition probabilities when adjacent sequence items must be different
Generating a random sequence from a fixed set of items is a common requirement, e.g., given the items A, B and C we might generate the sequence BACABCCBABC. Often the randomness is tempered by requirements such as each item having each item appear a given number of times in a sequence of a given length, e.g., in a random sequence of 100 items A appears 20 times, B 40 times and C 40 times. If there are rules about what pairs of items may appear in the sequence (e.g., no identical items adjacent to each other), then sequence generation starts to get a bit complicated.
Let’s say we want our sequence to contain: A 6 times, B 12 times and C 12 times, and no same item pairs to appear (i.e., no AA, BB or CC). The obvious solution is to use a transition matrix containing the probability of generating the next item to be added to the end of the sequence based on knowing the item currently at the end of the sequence.
My thinking goes as follows:
- given A was last generated there is an equal probability of it being followed by B or C,
- given B was last generated there is a 6/(6+12) probability of it being followed by A and a 12/(6+12) probability of it being followed by C,
- given C was last generated there is a 6/(6+12) probability of it being followed by A and a 12/(6+12) probability of it being followed by B.
giving the following transition matrix (this row by row approach having the obvious generalization to more items):
Second item
A B C
A 0 .5 .5
First
item B .33 0 .67
C .33 .67 0 |
Having read Generating constrained randomized sequences: Item frequency matters by Robert M. French and Pierre Perruchet (from whom I take these examples and algorithm on which the R code is based), I now know this algorithm for generating transition matrices is wrong. Before reading any further you might like to try and figure out why.
The key insight is that the number of XY pairs (reading the sequence left to right) must equal the number of YX pairs (reading right to left) where X and Y are different items from the fixed set (and sequence edge effects are ignored).
If we take the above matrix and multiply it by the number of each item we get the following (if A occurs 6 times it will be followed by B 3 times and C 3 times, if B occurs 12 times it will be followed by A 4 times and C 8 times, etc):
Second item
A B C
A 0 3 3
First
item B 4 0 8
C 4 8 0 |
which implies the sequence will contain AB 3 times when counted forward and BA 4 times when counted backwards (and similarly for AC/CA). This cannot happen, the matrix is not internally consistent.
The correct numbers are:
Second item
A B C
A 0 3 3
First
item B 3 0 9
C 3 9 0 |
giving the probability transition matrix:
Second item
A B C
A 0 .5 .5
First
item B .25 0 .75
C .25 .75 0 |
This kind of sequence generation occurs in testing and I wonder how many people have made the same mistake as me and scratched their heads over small deviations from the expected results.
The R code to calculate the transition matrix is straight forward but obscure unless you have the article to hand:
# Calculate expression (3) from: # Generating constrained randomized sequences: Item frequency matters # Robert M. French and Pierre Perruchet transition_count=function(item_count) { N_total=sum(item_count) # expected number of transitions ni_nj=(item_count %*% t(item_count))/(N_total-1) diag(ni_nj) = 0 # expected number of repeats d_k=item_count*(item_count-1)/(N_total-1) # Now juggle stuff around to put the repeats someplace else n=sum(ni_nj) n_k=rowSums(ni_nj) s_k=n - 2*n_k R_i=d_k / s_k R=sum(R_i) new_ij=ni_nj*(1-R) + (n_k %*% t(R_i)) + (R_i %*% t(n_k)) diag(new_ij)=0 return(new_ij) } transition_prob=function(item_count) { tc=transition_count(item_count) tp=tc / rowSums(tc) # relies on recycling return(tp) } |
the following calls:
transition_count(c(6, 12, 12)) transition_prob(c(6, 12, 12)) |
return the expected results.
French and Perruchet provide an Excel spreadsheet (note this contains a bug, the formula in cell F20 should start with F5 rather than F6).
Why do companies fix faults in software they sell?
Once I buy some software from a company they have my money, if sometime later I find a fault software what incentive does that company have to fix the software and provide me with an update (assuming the software is not so fault ridden that I take advantage of laws allowing me to return a purchase for a refund)?
There are three economic incentives for companies to fix faults:
- because I am paying them a fee for updates that include fixes to known faults,
- because they want to make future sales to me and to others (faults encountered by customers contribute towards the perception of product quality),
- they don’t want to lose money because a fault had consequences that resulted in legal action (this reason is overhyped, in practice software engineering has a missing dead body problem).
Which faults get fixed? Software is surprisingly fault-tolerant and there is no point in fixing faults that customers are unlikely to encounter. This means that once a product has been released and known to be acceptable to many customers, there is no incentive to actively search for faults; this means that the only faults likely to be fixed are the ones reported by customers.
When reporting a fault, customers are often asked to rate its severity. This is a useful technique for prioritizing what gets fixed first, or perhaps what does not get fixed at all. Customers who actively set out to find faults are not appreciated and are labelled as disruptive if they continue doing it. Finding faults is surprisingly easy, finding the faults that have a high probability of being encountered by customers and ranked by them as critical is very hard (this is one of the reasons static analysis tools are not widely used).
What is the motivation for developers to fix faults in Open Source?
- There are companies who provide support services for a fee, just like commercial offerings,
- Open Source is free, gaining more users is not an obvious incentive to fix faults. However, being known as the go-to guys for a given package is a way of attracting companies looking to hire somebody to provide support services or make custom modifications to that package. Fixing faults is a way of getting visibility, it is advertising.
- Developers hate the thought of doing something wrong resulting in a fault in code they have written, and writing faulty code is not socially acceptable behavior in software development circles. These feelings about what constitutes appropriate behavior are often enough to make developers want to spend time fixing faults in code they have written or feel responsible for, provided they have the time. I suspect a lot of faults get fixed by developers when their manager/wife thinks they are working on something more ‘useful’.
Generating code that looks like it is human written
I am very interested in understanding the patterns of developer behavior that lead to the human characteristics that can be found in code. To help me get some idea of how well I understand this behavior I have decided to build a tool that generates source code that appears to be written by human programmers. I hope to reach a point where I can offer a challenge to tell the difference between generated code and human written code.
The three main production techniques I plan to use are, in increasing order of relatedness to humans production techniques, are:
- Random generation based on percentage occurrence of language constructs obtained from measurements of existing source. This is the simplest approach and the one furthest away from common developer behavior; even so there are things that can be learned from this information. For instance, the theory that developers are more likely to create a function once code becomes heavily nested code implies that the probability of encountering an if-statement decreases as nesting depth increases; measurements show the probability of encountering an if-statement remaining approximately constant as depth of nesting increases.
- Behavior templates. People have habits in everyday life and also when writing software. While some habits are idiosyncratic and not encountered very often there are some that appear to be generally used. For instance, developers tend to assign a fixed role to every variable they define (e.g., stepper for stepping through a succession of values and most-recent holder holding the latest value encountered in going through a succession of values).
I am expecting/hoping that generation by behavioral templates will result in code having some of the probabilistic properties seen in human code, removing the need for purely random generation driven by low level language probability measurements. For instance, the probability of a local variable appearing in a function is proportional to the percentage of its previous occurrences up to that point in the source of the function (
percentage = occurrences_of_X / occurrences_of_all_local_variables) and I am hoping that this property appears as emergent behavior from generating using the role of variable template. - Story telling. A program is like the plot of a story, it has a cast of characters (e.g., classes, functions, libraries) that perform various actions and interact with each other in order to achieve various goals, there are subplots (intermediate results are calculated, devices are initialized, etc), there are resource limits, etc.
While a lot of stories are application domain specific there are subplots common to many stories; also how a story is told can be heavily influenced by the language used, for instance Prolog programs have a completely different structure than those written in procedural languages such as Java. I want to stay away from being application specific and I don’t plan to tackle languages too far outside the common-or-garden procedural variety.
Researchers have created automatic story generators; the early generators were template based while more recent systems have used an agent based approach. Story based generation of code is my ideal, but I am a long way away from having enough knowledge of developer behavior to be more than template based.
In a previous post I described a system for automatically generating very simply C programs. I plan to build on this system to incrementally improve the ‘humanness’ of the generated code. At some point, hopefully before the end of this year, I will challenge people to tell the difference between automatically generated and human written code.
The language I have studied the most is C and this will be the main target. I don’t want to be overly C specific and am trying to decide on a good second language (i.e., lots of source available for measurement, used by lots of developers and not too different from C). JavaScript is the current front runner, it is a class-less object oriented language which is not ‘wildly’ OO (the patterns of usage in human written OO code continue to evolve at a rapid rate which can make a lot of human C++/Java code look automatically generated).
As well as being a test bed for understanding of human generated code other uses for an automatic generator include compiler stress testing and providing code snippets to an automated fault fixing tool.
Compiler benchmarking for the 21st century
I would like to propose a new way of measuring the quality of a compiler’s code generator: The highest quality compiler is one that generates identical code for all programs that produce the same output, e.g., a compiler might spot programs that calculate pi and always generate code that uses the most rapidly converging method known. This is a very different approach to the traditional methods based on using (mostly) execution time or size (usually code but sometimes data) as a measure of quality.
Why is a new measurement method needed, and why choose this one? It is relatively easy for compiler vendors to tune their products to the commonly used benchmark and they seem to have lost their role as drivers for new optimization techniques. Different developers have different writing habits and companies should not have to waste time and money changing developer habits just to get the best quality code out of a compiler; compilers should handle differences in developer coding habits and not let it affect the quality of generated code. There are major savings to be had by optimizing the effect that developers are trying to achieve rather than what they have actually written (these days new optimizations targeting at what developers have written show very low percentage improvements).
Deducing that a function calculates pi requires a level of sophistication in whole program analysis that is unlikely to be available in production compilers for some years to come (ok, detecting 4*atan(1.0) is possible today). What is needed is a collection of compilable files containing source code that aims to achieve an outcome in lots of different ways. To get the ball rolling the “3n times 2” problem is presented as the first of this new breed of benchmarks.
The “3n times 2” problem is a variant on the 3n+1 problem that has been tweaked to create more optimization opportunities. One implementation of the “3n times 2” problem is:
if (is_odd(n)) n = 3*n+1; else n = 2*n; // this is n = n / 2; in the 3n+1 problem |
There are lots of ways of writing code that has the same effect, some of the statements I have seen for calculating n=3*n+1 include: n = n + n + n + 1, n = (n << 1) + n + 1 and n *= 3; n++, while some of the ways of checking if n is odd include: n & 1, (n / 2)*2 != n and n % 2.
I have created a list of different ways in which 3*n+1 might be calculated and is_odd(n) might be tested and written a script to generate a function containing all possible permutations (to reduce the number of combinations no variants were created for the least interesting case of n=2*n, which was always generated in this form). The following is a snippet of the generated code (download everything):
if (n & 1) n=(n << 2) - n +1; else n*=2; if (n & 1) n=3*n+1; else n*=2; if (n & 1) n += 2*n +1; else n*=2; if ((n / 2)*2 != n) { t=(n << 1); n=t+n+1; } else n*=2; if ((n / 2)*2 != n) { n*=3; n++; } else n*=2; |
Benchmarks need a means of summarizing the results and here I make a stab at doing that for gcc 4.6.1 and llvm 2.9, when executed using the -O3 option (output here and here). Both compilers generated a total of four different sequences for the 27 'different' statements (I'm not sure what to do about the inline function tests and have ignored them here) with none of the sequences being shared between compilers. The following lists the number of occurrences of each sequence, e.g., gcc generated one sequence 16 times, another 8 times and so on:
gcc 16 8 2 1 llvm 12 6 6 3
How might we turn these counts into a single number that enables compiler performance to be compared? One possibility is to award 1 point for each of the most common sequence, 1/2 point for each of the second most common, 1/4 for the third and so on. Using this scheme, gcc gets 20.625, and llvm gets 16.875. So gcc has greater consistency (I am loathed to use the much overused phrase higher quality).
Now for a closer look at the code generated.
Both compilers always generated code to test the least significant bit for the conditional expressions n & 1 and n % 2. For the test (n / 2)*2 != n gcc generated the not very clever right-shift/left-shift/compare while llvm and'ed out the bottom bit and then compared; so both compilers failed to handle what is a surprisingly common check for a number being odd.
The optimal code for n=3*n+1 on a modern x86 processor is (lots of register combinations are possible, let's assume rdx contains n) leal 1(%rdx,%rdx,2), %edx and this is what both compilers generated a lot of the time. This locally optimal code is not always generated because:
- gcc fails to detect that
(n << 2)-n+1is equivalent to(n << 1)+n+1and generates the sequenceleal 0(,%rax,4), %edx ; subl %eax, %edx ; addl $1, %edx(I pointed this out to a gcc maintainer sometime ago, and he suggested reporting it as a bug). This 'bug' occurs three times in total. - For some forms of the calculation llvm generates globally better code by taking the else arm into consideration. For instance, when the calculation is written as
n += (n << 1) +1llvm deduces that(n << 1)and the2*nin theelseare equivalent, evaluates this value into a register before performing the conditional test thus removing the need for an unconditional jump around the 'else' code:leal (%rax,%rax), %ecx testb $1, %al je .LBB0_8 # BB#7: orl $1, %ecx # deduced ecx is even, arithmetic unit not needed! addl %eax, %ecx .LBB0_8:
This more efficient sequence occurs nine times in total.
The most optimal sequence was generated by gcc:
testb $1, %dl leal (%rdx,%rdx), %eax je .L6 leal 1(%rdx,%rdx,2), %eax .L6: |
with llvm and pre 4.6 versions of gcc generating the more traditional form (above, gcc 4.6.1 assumes that the 'then' arm is the most likely to be executed and trades off a leal against a very slow jmp):
testb $1, %al je .LBB0_5 # BB#4: leal 1(%rax,%rax,2), %eax jmp .LBB0_6 .LBB0_5: addl %eax, %eax .LBB0_6: |
There is still room for improvement, perhaps by using the conditional move instruction (which gcc actually generates within the not-very-clever code sequence for (n / 2)*2 != n) or by using the fact that eax already holds 2*n (the potential saving would come through a reduction in complexity of the internal resources needed to execute the instruction).
llvm insists on storing the calculated value back into n at the end of every statement. I'm not sure if this is a bug or a feature designed to make runtime debugging easier (if so it ought to be switched off by default).
Missed optimization opportunities (not intended to be part of this benchmark and if encountered would require a restructuring of the test source) include noticing that if  is odd then
is odd then 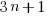 is always even, creating the opportunity to perform the following multiply by 2 without an if test.
is always even, creating the opportunity to perform the following multiply by 2 without an if test.
Perhaps one day, compilers will figure out when a program is calculating pi and generate code that uses the best known algorithm. In the meantime, I am interested in hearing suggestions for additional different-algorithm-same-code benchmarks.
Simple generator for compiler stress testing source
Since writing my C book I have been interested in the problem of generating source that has the syntactic and semantic statistical characteristics of human written code.
Generating code that obeys a language’s syntax is straight forward. Take a specification of the syntax (say is some yacc-like form) and ‘generate’ each of the terminals/nonterminals on the right-hand-side of the start symbol. Nonterminals will lead to rules having right-hand-sides that in turn need to be ‘generated’, a random selection being made when a nonterminal has more than one possible rhs rule. Output occurs when a terminal is ‘generated’.
For the code to mimic human written code it is necessary to bias the random selection process; a numeric value at the start of each rhs rule can be used to specify the percentage probability of that rule being chosen for the corresponding nonterminal.
The following example generates a subset of C expressions; nonterminals in lowercase, terminals in uppercase and implemented as a call to a function having that name:
%grammar first_rule : def_ident " = " expr " ;n" END_EXPR_STMT ; def_ident : MK_IDENT ; constant : MK_CONSTANT ; identifier : KNOWN_IDENT ; primary_expr : 30 constant | 60 identifier | 10 " (" expr ") " ; multiplicative_expr : 50 primary_expr | 40 multiplicative_expr " * " primary_expr | 10 multiplicative_expr " / " primary_expr ; additive_expr : 50 multiplicative_expr | 25 additive_expr " + " multiplicative_expr | 25 additive_expr " - " multiplicative_expr ; expr : START_EXPR additive_expr FINISH_EXPR ; |
A 250 line awk program (awk only because I use it often enough for simply text processing that it is second nature) translates this into two Python lists:
productions = [ [0], [ 1, 1, 1, # first_rule 0, 5, [2, 1001, 3, 1002, 1003, ], ], [ 2, 1, 1, # def_ident 0, 1, [1004, ], ], [ 4, 1, 1, # constant 0, 1, [1005, ], ], [ 5, 1, 1, # identifier 0, 1, [1006, ], ], [ 6, 3, 0, # primary_expr 30, 1, [4, ], 60, 1, [5, ], 10, 3, [1007, 3, 1008, ], ], [ 7, 3, 0, # multiplicative_expr 50, 1, [6, ], 40, 3, [7, 1009, 6, ], 10, 3, [7, 1010, 6, ], ], [ 8, 3, 0, # additive_expr 50, 1, [7, ], 25, 3, [8, 1011, 7, ], 25, 3, [8, 1012, 7, ], ], [ 3, 1, 1, # expr 0, 3, [1013, 8, 1014, ], ], ] terminal = [ [0], [ STR_TERM, " = "], [ STR_TERM, " ;n"], [ FUNC_TERM, END_EXPR_STMT], [ FUNC_TERM, MK_IDENT], [ FUNC_TERM, MK_CONSTANT], [ FUNC_TERM, KNOWN_IDENT], [ STR_TERM, " ("], [ STR_TERM, ") "], [ STR_TERM, " * "], [ STR_TERM, " / "], [ STR_TERM, " + "], [ STR_TERM, " - "], [ FUNC_TERM, START_EXPR], [ FUNC_TERM, FINISH_EXPR], ] |
which can be executed by a simply interpreter:
def exec_rule(some_rule) : rule_len=len(some_rule) cur_action=0 while (cur_action < rule_len) : if (some_rule[cur_action] > term_start_base) : gen_terminal(some_rule[cur_action]-term_start_base) else : exec_rule(select_rule(productions[some_rule[cur_action]])) cur_action+=1 productions.sort() start_code() ns=0 while (ns < 2000) : # Loop generating lots of test cases exec_rule(select_rule(productions[1])) ns+=1 end_code() |
Naive syntax-directed generation results in a lot of code that violates one or more fundamental semantic constraints. For instance the assignment (1+1)=3 is syntactically valid in many languages, which invariably specify a semantic constraint on the lhs of an assignment operator being some kind of modifiable storage location. The simplest solution to this problem is to change the syntax to limit the kinds of constructs that can be generated on the lhs of an assignment.
The hardest semantic association to get right is the connection between variable declarations and references to those variables in expressions. One solution is to mimic how I think many developers write code, that is to generate the statements first and then generate the required definitions for the appropriate variables.
A whole host of minor semantic issues require the syntax generated code to be tweaked, e.g., division by zero occurs more often in untweaked generated code than human code. There are also statistical patterns within the semantics of human written code, e.g., frequency of use of local variables, that need to be addressed.
A few weeks ago the source of Csmith, a C source generator designed to stress the code generation phase of a compiler, was released. Over the years various people have written C compiler stress testers, most recently NPL implemented one in Java, but this is the first time that the source has been released. Imagine my disappointment on discovering that Csmith contained around 40 KLOC of code, only a bit smaller than a C compiler I had once help write. I decided to see if my ‘human characteristics’ generator could be used to create a compiler code generator stress tester.
The idea behind compiler code generator stress testing is to generate a program containing some complicated sequence of code, compile and run it, comparing the value produced against the value that is supposed to be produced.
I modified the human characteristics generator to produce pairs of statements like the following:
i = i_3 * i_6 & i_2 << i_7 ; chk_result(i, 3 * 6 & 2 << 7, __LINE__); |
the second argument to chk_result is the value that i should contain (while generating the expression to assign to i the corresponding constant expression with the variables replaced by their known values is also created).
Having the compiler evaluate the constant expression simplifies the stress tester and provides another check that the compiler gets things right (or gets two different things wrong in the same way, in which case we probably don’t get to see any failure message). The first gcc bug I found concerned this constant expression (in fact this same compiler bug crops up with alarming regularity in the generated code).
As previously mentioned connecting variables in expressions to a corresponding definition is a lot of work. I simplified this problem by assuming that an integer variable i would be predefined in the surrounding support code and that this would be the only variable ever assigned to in the generated code.
There is some simple house-keeping that wraps everything within a program and provides the appropriate variable definitions.
The grammar used to generate full C expressions is 228 lines, the awk translator 252 lines and the Python interpreter 55 lines; just over 1% of Csmith in LOC and it is very easy to configure. However, an awful lot functionality needs to be added before it starts to rival Csmith, not least of which is support for assignment to more than one integer variable!
Quality comparison of floating-point maths libraries
What is the best way to compare the quality of floating-point math libraries (e.g., sin, cos and log)? The traditional approach for evaluating the quality of an algorithm implementing a mathematical function is based on mathematics; methods have been developed to calculate the maximum error between the calculated and the actual value. The answer produced by this approach does not say anything about how frequently this maximum error will occur, only that it occurs at least once.
The log (natural logarithm) is probably the most frequently used mathematical function and I decided to compare a few implementations; R statistical package version 2.11.1 and glibc (libm version 2.11.2) both running under Suse 11.3 on an AMD Athlon 64 X2, and Cygwin version 1.7.1 under Windows XP SP 2 on another AMD Athlon 64 X2.
The algorithm often used to implement mathematical functions involves evaluating a polynomial expression (e.g., Chebyshev polynomials) within a small range of values (various methods are used to map the argument into this range and then scale the calculated result). I decided to initially treat the implementations under test as black boxes and did not know the ranges they used; a range of 0.1 to 1.0 seemed like a good idea and I generated all single precision floating-point values between these two bounds (all 28,521,267 of them, with each adjacent pair still having 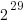 double precision values between them).
double precision values between them).
#include <math.h> #include <stdio.h> int main(int argc, char *argv[]) { float val = 0.1, max_val = 1.0; while (val < max_val) { printf("%12.10f\n", val); val=nextafterf(val, 1.1); } } |
This list of 28 million values was fed as input to three programs:
- bc, which was used to generate the list of assumed to be correct logarithm of these 28 million values. R supports 64-bit IEEE compliant floating-point values, as do the C compilers/libraries used, and the number of decimal digits supported in this representation is 15. To provide greater accuracy to compare against the values generated by bc contained 17 digits, an extra two decimal digits over the IEEE values.
scale=17 while ((val=read() > 0)) l(val)
- A C program.
#include <math.h> #include <stdio.h> int main(int argc, char *argv[]) { double val; while (!feof(stdin)) { scanf("%lf", &val); printf("%17.15f\n", log(val)); } }
- A R program.
base_range=file("stdin", open="r") base_val=as.numeric(readLines(base_range, n=1)) while (length(base_val) != 0) { cat(format(log(base_val), nsmall=15), file=stdout()) cat("\n", file=stdout()) base_val=as.numeric(readLines(base_range, n=1)) }
The output of the C and R programs was then compared against the output from bc; which unfortunately creates a dependency on the accuracy of the C & R binary to decimal output routines (the subsequent comparison process gets around the decimal-to-binary input problem by reading the log values as strings and comparing the last few digits of each respective value). Accurate floating-point I/O needs something like hexadecimal floating constants.
Plotting the number of computed values of log that differ by a given amount from the value computed by bc, we get (values whose error is below -50 will be rounded down and those above 50 rounded up, ignoring the issue of round to even):
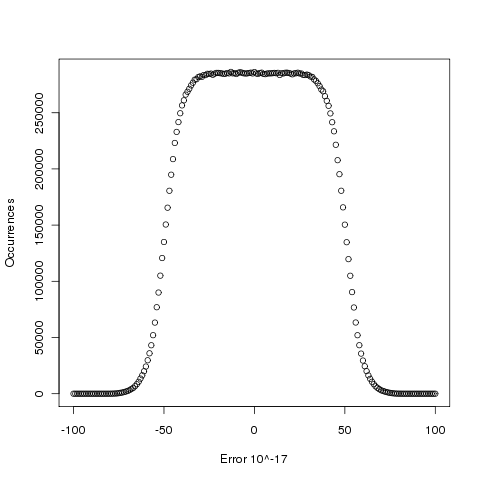
The results (raw data for R, Linux C and Cygwin C) show that around 5.6% of values are off by one in the last (15th) digit (Cygwin was slightly worse at 5.7%). The results for R/Linux C were almost identical and a quick check of the R source tree showed that R calls the C library function to evaluate log (it is a bit worrying that R is dependent on the host maths library, they should think about replacing this dependency by something like MPFR tout suite; even though the 64-bit glibc library is of very high quality it still has an environmental dependency).
Being off by one in the last decimal place is unlikely to keep many people awake at night. But if we want a measure of quality, is percentage of inaccurate values a useful measure of math library quality? Provided it is coupled with the amount of inaccuracy, I think this is a useful measure.
Variations in the literal representation of Pi
The numbers system I am developing attempts to match numeric literals contained in a file against a database of interesting numbers. One of the things I did to quickly build a reasonably sized database of reliable values was to extract numeric literals from a few well known programs that I thought I could trust.
R is a widely used statistical package, and Maxima is a computer algebra system with a long history. Both contain a great deal of functionality and are actively maintained.
To my surprise, the source code of both packages contain a large variety of different literal values for  , or to be exact, the number of digits contained in the literals varied by more than I expected. In the following table, the value to the left of the
, or to be exact, the number of digits contained in the literals varied by more than I expected. In the following table, the value to the left of the  representation is the number of occurrences; values listed in increasing literal order:
representation is the number of occurrences; values listed in increasing literal order:
Maxima R
2 3.14159
14 3.141592
1 3.1415926
1 3.14159265 2 3.14159265
3 3.1415926535
4 3.14159265358979
14 3.141592653589793
3 3.1415926535897932385 3 3.1415926535897932385
9 3.14159265358979324
1 3.14159265359
1 3.1415927
1 3.141593
The comments in the Maxima source led me to believe that some thought had gone into ensuring that the numerical routines were robust. Over 3/4 of the literal representations of  have a precision comparable to at least that of 64-bit floating-point (I’m assuming an IEEE 754 representation in this post).
have a precision comparable to at least that of 64-bit floating-point (I’m assuming an IEEE 754 representation in this post).
In the R source, approximately 2/3 of the literal representations of  have a precision comparable to that of 32-bit floating-point.
have a precision comparable to that of 32-bit floating-point.
Closer examination of the source suggests one reason for this difference. Both packages make heavy use of existing code (translated from Fortran to Lisp for Maxima and from Fortran to C for R); using existing code makes good sense and because of its use in scientific and engineering applications many numerical libraries have been written in Fortran. Maxima has adapted the slatec library, whereas the R developers have used a variety of different libraries (e.g., specfun).
How important is variation in the representation of Pi?
- A calculation based on a literal that is only accurate to 32-bits is likely to be limited to that level of accuracy (unless errors cancel out somewhere).
- Inconsistencies in the value used to represent Pi are a source of error. These inconsistencies may be implicit, for instance literals used to denote a value derived from
 such as
such as 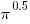 often seem to be based on more precise values of Pi than appear in the code.
often seem to be based on more precise values of Pi than appear in the code.
The obvious solution to this representation issue of creating a file containing definitions of all the frequently used literal values has possible drawbacks. For instance, numerical accuracy is a strange beast, and increasing the precision of one literal without doing the same for other literals appearing in a calculation can sometimes reduce the accuracy of the final result.
Pulling together existing libraries to build a package is often very cost-effective, but numerical accuracy is a slippery beast, and this inconsistent usage of literals suggests that developers from these two communities have not addressed the system level consequences of software reuse.
Update 6 April: After further rummaging around in the R source distribution, I found that things are not as bad as they first appear. Only two of the single precision instances of  listed above occur in the C or Fortran source code, the rest appear in support files (e.g., m4 scripts and R examples).
listed above occur in the C or Fortran source code, the rest appear in support files (e.g., m4 scripts and R examples).
Distribution of numeric values (additive)
Developers and testers rarely put any thought into working out the likely distribution of numeric values (final or intermediate) computed during the execution of the code they write.
The likely value of a variable is useful to know in a number of situations, including optimizing code (should it prove to be necessary) for the common case and testing (what distribution of input values are needed to be confident that all paths through a program are exercised?)
The answer for the ‘simple’ distributions is actually more complicated to work with than the more ‘complicated’ distributions. For instance, the sum of two independent values having a normal distributions is a normal distribution and the sum of two Poisson distributions is also a Poisson distribution.
What if the values are uniformly distributed? If two independent, randomly chosen, uniformly distributed, variables, are added what is the distribution of the result? For instance, if the values of X and Y are independent of each other and take on any value between 0 and 9, with equal likelihood, what is the most (and least) likely value of X+Y?
Warning: Information spoilers follow.
You are probably thinking that the result will also be uniformly distributed and indeed it would be if the range of values taken by X and Y did not overlap. When the possible range of values overlap exactly the answer is the triangular distribution, with the mostly likely result being 9 and the least likely results being 0 and 18.
The variance of the actual result distribution is approximately six times smaller than the original distribution, meaning that the common cases occupy a much narrower value range. This value range ‘narrowing’ goes someway towards helping to explain the surprising discovery that during program execution a small set of (integer and floating) values often occur with such regularity that it might be worth cpu arithmetic units remembering previous operands and their results (i.e., to save time by returning the result rather than recalculating it).
Recent Comments