Archive
Remotivating data analysed for another purpose
The motivation for fitting a regression model has a major impact on the model created. Some of the motivations include:
- practicing software developers/managers wanting to use information from previous work to help solve a current problem,
- researchers wanting to get their work published seeks to build a regression model that show they have discovered something worthy of publication,
- recent graduates looking to apply what they have learned to some data they have acquired,
- researchers wanting to understand the processes that produced the data, e.g., the author of this blog.
The analysis in the paper: An Empirical Study on Software Test Effort Estimation for Defense Projects by E. Cibir and T. E. Ayyildiz, provides a good example of how different motivations can produce different regression models. Note: I don’t know and have not been in contact with the authors of this paper.
I often remotivate data from a research paper. Most of the data in my Evidence-based Software Engineering book is remotivated. What a remotivation often lacks is access to the original developers/managers (this is often also true for the authors of the original paper). A complicated looking situation is often simplified by background knowledge that never got written down.
The following table shows the data appearing in the paper, which came from 15 projects implemented by a defense industry company certified at CMMI Level-3.
Proj Test Req Test Meetings Faulty Actual Scenarios
Plan Rev Env Scenarios Effort
Time Time
P1 144.5 1.006 85 60 100 2850 270
P2 25.5 1.001 25.5 4 5 250 40
P3 68 1.005 42.5 32 65 1966 185
P4 85 1.002 85 104 150 3750 195
P5 198 1.007 123 87 110 3854 410
P6 57 1.006 35 25 20 903 100
P7 115 1.003 92 55 56 2143 225
P8 81 1.009 156 62 72 1988 287
P9 388 1.004 150 208 553 13246 1153
P10 177 1.008 93 77 157 4012 360
P11 62 1.001 175 186 199 5017 310
P12 111 1.005 116 82 143 3994 423
P13 63 1.009 188 177 151 3914 226
P14 32 1.008 25 28 6 435 63
P15 167 1.001 177 143 510 11555 1133 |
where: TestPlanTime is the test plan creation time in hours, ReqRev is the test/requirements review of period in hours, TestEnvTime is the test environment creation time in hours, Meetings is the number of meetings, FaultyScenarios is the number of faulty test scenarios, Scenarios is the number of Scenarios, and ActualEffort is the actual software test effort.
Industrial data is hard to obtain, so well done to the authors for obtaining this data and making it public. The authors fitted a regression model to estimate software test effort, and the model that almost perfectly fits to actual effort is:
ActualEffort=3190 + 2.65*TestPlanTime
-3170*ReqRevPeriod - 3.5*TestEnvTime
+10.6*Meetings + 11.6*FaultScrenarios + 3.6*Scenarios |
My reading of this model is that having obtained the data, the authors felt the need to use all of it. I have been there and done that.
Why all those multiplication factors, you ask. Isn’t ActualTime simply the sum of all the work done? Yes it is, but the above table lists the work recorded, not the work done. The good news is that the fitted regression models shows that there is a very high correlation between the work done and the work recorded.
Is there a simpler model that can be used to explain/predict actual time?
Looking at the range of values in each column, ReqRev varies by just under 1%. Fitting a model that does not include this variable, we get (a slightly less perfect fit):
ActualEffort=100 + 2.0*TestPlanTime
- 4.3*TestEnvTime
+10.7*Meetings + 12.4*FaultScrenarios + 3.5*Scenarios |
Simple plots can often highlight patterns present in a dataset. The plot below shows every column plotted against every other column (code+data):

Points forming a straight line indicate a strong correlation, and the points in the top-right ActualEffort/FaultScrenarios plot look straight. In fact, this one variable dominates the others, and fits a model that explains over 99% of the deviation in the data:
ActualEffort=550 + 22.5*FaultScrenarios |
Many of the points in the ActualEffort/Screnarios plot are on a line, and adding Meetings data to the model explains just under 99% of the variance in the data:
actualEffort=-529.5
+15.6*Meetings + 8.7*Scenarios |
Given that FaultScrenarios is a subset of Screnarios, this connectedness is not surprising. Does the number of meetings correlate with the number of new FaultScrenarios that are discovered? Questions like this can only be answered by the original developers/managers.
The original data/analysis was interesting enough to get a paper published. Is it of interest to practicing software developers/managers?
In a small company, those involved are likely to already know what these fitted models are telling them. In a large company, the left hand does not always know what the right hand is doing. A CMMI Level-3 certified defense company is unlikely to be small, so this analysis may be of interest to some of its developer/managers.
A usable estimation model is one that only relies on information available when the estimation is needed. The above models all rely on information that only becomes available, with any accuracy, way after the estimate is needed. As such, they are not practical prediction models.
Sampling error in software engineering
In the physical sciences, measurement error occurs because of accuracy limits on the device used to make the measurement and the interpretation of the data by the person doing the measurement.
In software engineering, some measurements appear to be error free. For instance, lines of code is a discrete value that is easily counted. While some people don’t include blank lines and/or comments, the choice of what to count does not prevent an exact count being made.
In physics, the behavior of particular elements does not depend on the identity of which atoms are measured, while in software the behavior of programs written to the same specification can have different characteristics, e.g., lines of code.
For instance, each implementation of the 3n+1 problem will contain some number of LOC, with other implementations often containing a different number of LOC. The plot below shows the distribution of LOC for 6,301 implementations of 3n+1 (code and data):
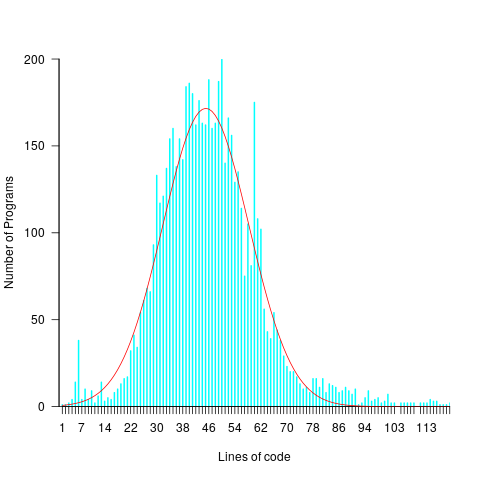
Each program implementing the 3n+1 problem is one sample from the population of programs implementing the 3n+1 specification. Different people are likely to implement different programs, and the same person may create different implementations at different times.
Sampling error occurs when the characteristics of a sample are used to infer characteristics about the population from which the sample was drawn.
How might sampling error affect the results of data analysis?
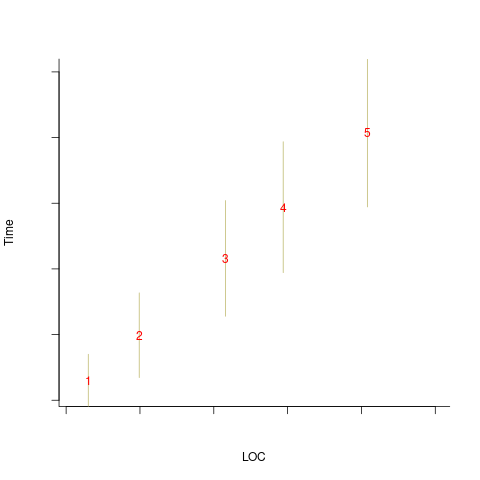
An example, using made-up values: Assume that two sets of sample measurements are made of the time taken to implement five different specifications, along with the lines of code contained in the implementations (in the same language). In the plot below, the yellow circles show a range of likely implementation measurements for each of the five specifications. The green dots, one for each specification, are measurements of one sample of programs implementing each specification; the blue dots are a second sample of programs (code):

The green and blue lines show the ordinary least squares regression model fitted to each sample. The different samples selected from the five populations has produced what appears to be slightly different models. How significant is this difference in the fitted models?
The grey line denotes where LOC is proportional to implementation time, which is one hypothesis of software project progress. The green line sample implies that LOC growth decreases as implementation time increases, while the blue line sample implies the reverse (both have been proposed as hypotheses of software project progress).
The difference in this example is important because the models fitted to the samples straddle the demarcation line between alternative theories of software project development.
A larger sample may not produce a more accurate model; a previous post analyses such a case. The example above shows a symmetric uniformly distributed population because that is the easiest to plot. In practice, populations distributions are likely to be asymmetric and irregular, e.g., measured time may be rounded to the nearest appropriate unit.
The mathematics underpinning OLS assumes that there is no error in the explanatory variables (LOC in the above plot), and that all the error is concentrated in the response variable (Time in the above plot). When there is a non-trivial sample error, or measurement error, OLS is not the appropriate technique to use to fit a regression model. The plot below shows the sample error that is assumed by OLS (code):
When there is a non-trivial error in the explanatory variable (LOC in this example), the appropriate technique for fitting a regression model is errors-in-variables regression.
Building an errors-in-variables regression model requires values for the error in the variables appearing in the equation to be fitted. Obtaining these values can be very difficult (Deming regression is a fitting technique based on the ratio of the errors).
In the above example, what is the likely variability in the implementation time and LOC, for a given specification? The limited data on the LOC contained in multiple implementations of the same specification suggests that the standard deviation of the LOC across implementations of the same specification is around 25% of the mean.
Learning researchers have run experiments where each subject performs the same task multiple times. Performance improves with practice, which makes it difficult to calculate the likely variability in the first-time performance.
My book: Evidence-based software engineering recommends using SIMEX to fit errors-in-variables models (section 11.2.3). This technique takes a model fitted using existing methods (allowing a wide range of models to be fitted), and then refits the model created based on the estimated error in one or more explanatory variables (no need to estimate an error in the response variable, the technique makes use of the value from the initial fit).
Predicting the size of the Linux kernel binary
How big is the binary for the Linux kernel? Depending on the value of around 15,000 configuration options, the size of the version 5.8 binary could be anywhere between 7.3Mb and 2,134 Mb.
Who is interested in the size of the Linux kernel binary?
We are not in the early 1980s, when memory for a desktop microcomputer often topped out at 64K, and software was distributed on 360K floppies (720K when double density arrived; my companies first product was a code optimizer which reduced program size by around 10%).
While desktop systems usually have oodles of memory (disk and RAM), developers targeting embedded systems seek to reduce costs by minimizing storage requirements, security conscious organizations want to minimise the attack surface of the programs they run, and performance critical systems might want a kernel that fits within a processors’ L2/L3 cache.
When management want to maximise the functionality supported by a kernel within given hardware resource constraints, somebody gets the job of building kernels supporting various functionality to find out the size of the binaries.
At around 4+ minutes per kernel build, it’s going to take a lot of time (or cloud costs) to compare lots of options.
The paper Transfer Learning Across Variants and Versions: The Case of Linux Kernel Size by Martin, Acher, Pereira, Lesoil, Jézéquel, and Khelladi describes an attempt to build a predictive model for the size of the kernel binary. This paper includes an extensive list of references.
The author’s approach was to first obtain lots of kernel binary sizes by building lots of kernels using random permutations of on/off options (only on/off options were changed). Seven kernel versions between 4.13 and 5.8 were used, producing 243,323 size/option setting combinations (complete dataset). This data was used to train a machine learning model.
The accuracy of the predictions made by models trained on a single kernel version were accurate within that kernel version, but the accuracy of single version trained models dropped dramatically when used to predict the binary size of later kernel versions, e.g., a model trained on 4.13 had an accuracy of 5% MAPE predicting 4.13, when predicting 4.15 the accuracy is 20%, and 32% accurate predicting 5.7.
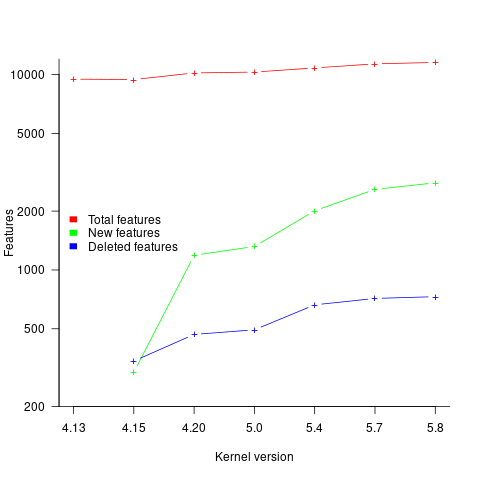
I think that the authors’ attempt to use this data to build a model that is accurate across versions is doomed to failure. The rate of change of kernel features (whose conditional compilation is supported by one or more build options) supported by Linux is too high to be accurately modelled based purely on information of past binary sizes/options. The plot below shows the total number of features, newly added, and deleted features in the modelled version of the kernel (code+data):
What is the range of impacts of each build option, on binary size?
If each build option is independent of the others (around 44% of conditional compilation directives in the kernel source contain one option), then the fitted coefficients of a simple regression model gives the build size increment when the corresponding option is enabled. After several cpu hours, the 92,562 builds involving 9,469 options in the version 4.13 build data were fitted. The plot below shows a sorted list of the size contribution of each option; the model 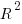 is 0.72, i.e., quite a good fit (code+data):
is 0.72, i.e., quite a good fit (code+data):
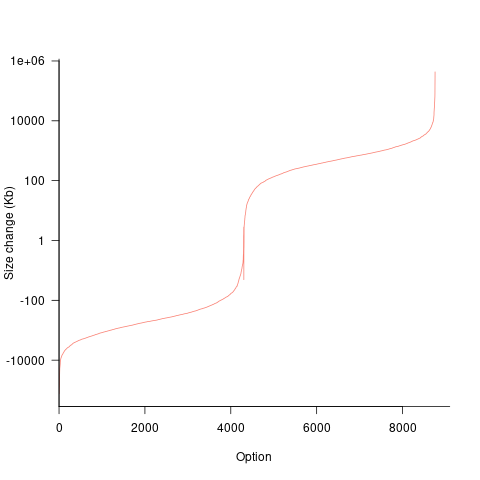
While the mean size increment for an enabled option is 75K, around 40% of enabled options decreases the size of the kernel binary. Modelling pairs of options (around 38% of conditional compilation directives in the kernel source contain two options) will have some impact on the pattern of behavior seen in the plot, but given the quality of the current model (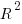 is 0.72) the change is unlikely to be dramatic. However, the simplistic approach of regression fitting the 90 million pairs of option interactions is not practical.
is 0.72) the change is unlikely to be dramatic. However, the simplistic approach of regression fitting the 90 million pairs of option interactions is not practical.
What might be a practical way of estimating binary size for any kernel version?
The size of a binary is essentially the quantity of code+static data it contains.
An estimate of the quantity of conditionally compiled source code dependent on a given option is likely to be a good proxy for that option’s incremental impact on binary size.
It’s trivial to scan source code for occurrences of options in conditional compilation directives, and with a bit more work, the number of lines controlled by the directive can be counted.
There has been a lot of evidence-based research on software product lines, and feature macros in particular. I was expecting to find a dataset listing the amount of code controlled by build options in Linux, but the data I can find does not measure Linux.
The Martin et al. build data is perfectfor creating a model linking quantity of conditionally compiled source code to change of binary size.
Multi-state survival modeling of a Jira issues snapshot
Work items in a formal development process progress through a series of stages, e.g., starting at Open, perhaps moving to Withdrawn or Merged with another item, eventually reaching Development, and finishing at Done (with a few being Reopened, i.e., moving back to the start of the process).
This process can be modelled as a Markov chain, provided data on each stage of the process is available, for each work item; allowing values such as average time spent in each state and transition probabilities to be calculated.
The Jira issue/task/bug/etc tracking system has an option to generate a snapshot of the current status of work items in the system. The snapshot information on each item includes: start-date, current-state, time-in-state, date-of-snapshot.
If we assume that all work items pass through the same sequence of states, from Open to Done, then the snapshot contains enough information to build a multi-state survival model.
The key information is time-in-state, which can be used to calculate the date/time when an item transitioned from its previous state to its current state, providing a required link between all states.
How is a multi-state survival model better than creating a distinct survival model for each state?
The calculation of each state in a multi-state model takes into account information from the succeeding state, i.e., the time-in-state value in the succeeding state provides timing (from the Start state) on when a work item transitioned from its previous state. While this information could be added to each of the distinct models, it’s simpler to bundle everything together in one model.
A data analysis article by Robert Krasinski linked to the data used 🙂 The data does not include a description of the columns, but most of the names appear self-explanatory (I have no idea what key might be). Each of the 3,761 rows includes a story-point estimate, team-id, and a tag name for the work item.
Building a multi-state model provides a means for estimating the impact of team-id and story-points on time-in-state. I would expect items with higher story-point estimates to spend longer in Development, but I’m not sure how much difference there will be on other states.
I pruned the 22 states present in the data down to the following sequence of 13. Items might be Withdrawn or Merged with others items at any time, but I’m keeping things simple. These two states should also be absorbing in that there is no exit from them, I faked this by adding a transition to Done.
Open
Withdrawn
Merged
Backlog
In Analysis
In Refinement
Ready for Development
In Development
Code Review
Ready for Test
In Testing
Ready for Signoff
Done |
I’m familiar with building survival models, but have only ever built a couple of multi-state survival models. R supports several packages, which is the best one to use for this minimalist multi-state dataset?
The msm package is very much into state transition probabilities, or at least that is the impression I got from reading its manual. flexsurv and mstate are other packages I looked at. I decided to stay with the survival package, the default for simpler problems; the manuals contained lots of examples and some of them appeared similar to my problem.
Each row of work item information in the Jira snapshot looks something like the following:
X daysInStatus start status obsdate 1 0.53 2020-05-12 In Development 2020-05-18 |
This work item transitioned from state Ready for Development at time 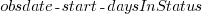 to state In Development at time
to state In Development at time 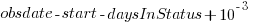 , and was still in state In Development at time
, and was still in state In Development at time 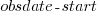 (when the snapshot was taken); the
(when the snapshot was taken); the 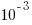 is a small interval used to separate the states.
is a small interval used to separate the states.
As is often the case with R packages, most of the work went into figuring out how to call the library functions with the data formatted just so, plus of course my own misunderstandings. Once the data was cleaned and process, the analysis was one line of code plus one to print the results; for instance, to estimate the mean time in each state by story-point value (code+data):
sp_fit=survfit(Surv(tstop-tstart, state) ~ sp, data=merged_status) print(sp_fit) |
Given the uncertainties in this model building process, I’m not going to discuss the results. This post is a proof of concept, which others can apply when the sequence of states is known with some degree of confidence, and good reasons for noise in the data are available.
Including natural language text topics in a regression model
The implementation records for a project sometimes include a brief description of each task implemented. There will be some degree of similarity between the implementation of some tasks. Is it possible to calculate the degree of similarity between tasks from the text in the task descriptions?
Over the years, various approaches to measuring document similarity have been proposed (more than you probably want to know about natural language processing).
One of the oldest, simplest and widely used technique is term frequency–inverse document frequency (tf-idf), which is based on counting word frequencies, i.e., is word context is ignored. This technique can work well when there are a sufficient number of words to ensure a good enough overlap between similar documents.
When the description consists of a sentence or two (i.e., a summary), the problem becomes one of sentence similarity, not document similarity (so tf-idf is unlikely to be of any use).
Word context, in a sentence, underpins the word embedding approach, which represents a word by an n-dimensional vector calculated from the local sentence context in which the word occurs (derived from a large amount of text). Words that are closer, in this vector space, are expected to have similar meanings. One technique for calculating the similarity between sentences is to compare the averages of the word embedding of the words they contain. However, care is needed; words appearing in the same context can create sentences having different meanings, as in the following (calculated sentence similarity in the comments):
import spacy nlp=spacy.load("en_core_web_md") # _md model needed for word vectors nlp("the screen is black").similarity(nlp("the screen is white")) # 0.9768339369182919 # closer to 1 the more similar the sentences nlp("implementing widgets would be little effort").similarity(nlp("implementing widgets would be a huge effort")) # 0.9636533803238744 nlp("the screen is black").similarity(nlp("implementing widgets would be a huge effort")) # 0.6596892830922606 |
The first pair of sentences are similar in that they are about the characteristics of an object (i.e., its colour), while the second pair are similar in that are about the quantity of something (i.e., implementation effort), and the third pair are not that similar.
The words in a document, or summary, are about some collection of topics. A set of related documents are likely to contain a discussion of a set of related topics in varying degrees. Latent Dirichlet allocation (LDA) is a widely used technique for calculating a set of (unseen) topics from a set of documents and their contained words.
A recent paper attempted to estimate task effort based on the similarity of the task descriptions (using tf-idf). My last semi-serious attempt to extract useful information from text, some years ago, was a miserable failure (it’s a very hard problem). Perhaps better techniques and tools are now available for me to leverage (my interest is in understanding what is going on, not making predictions).
My initial idea was to extract topics from task data, and then try to add these to regression models of task effort estimation, to see what impact they had. Searching to find out what researchers have recently been doing in this area, I was pleased to see that others were ahead of me, and had implemented R packages to do the heavy lifting, in particular:
- The
stmpackage supports the creation of Structural Topic Models; these add support for covariates to influence the process of fitting LDA models, i.e., a correlation between the topics and other variables in the data. Uses of STM appear to be oriented towards teasing out differences in topics associated with different values of some variable (e.g., political party), and the package authors have written papers analysing political data. - The
psychtmpackage supports what the authors call supervised latent Dirichlet allocation with covariates (SLDAX). This handles all the details needed to include the extracted LDA topics in a regression model; exactly what I was after. The user interface and documentation for this package is not as polished as thestmpackage, but the code held together as I fumbled my way through.
To experiment using these two packages I used the SiP dataset, which includes summary text for each task, and I have previously analysed the estimation task data.
The stm package:
The textProcessor function handles all the details of converting a vector of strings (e.g., summary text) to internal form (i.e., handling conversion to lower case, removing stop words, stemming, etc).
One of the input variables to the LDA process is the number of topics to use. Picking this value is something of a black art, and various functions are available for calculating and displaying concepts such as topic semantic coherence and exclusivity, the most commonly used words associated with a topic, and the documents in which these topics occur. Deciding the extent to which 10 or 15 topics produced the best results (values that sounded like a good idea to me) required domain knowledge that I did not have. The plot below shows the extent to which the words in topic 5 were associated with the Category column having the value “Development” or “Management” (code+data):
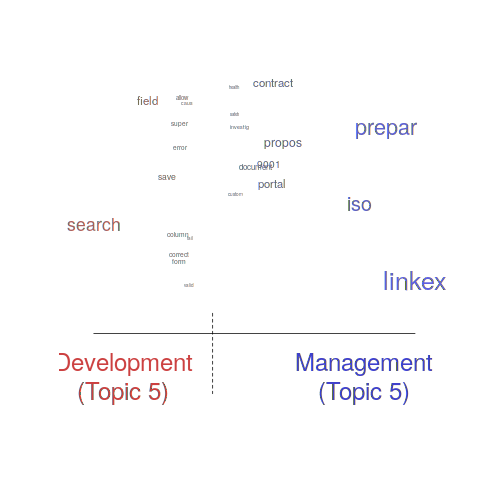
The psychtm package:
The prep_docs function is not as polished as the equivalent stm function, but the package’s first release was just last year.
After the data has been prepared, the call to fit a regression model that includes the LDA extracted topics is straightforward:
sip_topic_mod=gibbs_sldax(log(HoursActual) ~ log(HoursEstimate), data = cl_info,
docs = docs_vocab$documents, model = "sldax",
K = 10 # number of topics) |
where: log(HoursActual) ~ log(HoursEstimate) is the simplest model fitted in the original analysis.
The fitted model had the form: 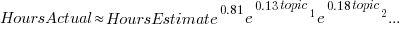 , with the calculated coefficient for some topics not being significant. The value
, with the calculated coefficient for some topics not being significant. The value 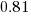 is close to that fitted in the original model. The value of
is close to that fitted in the original model. The value of 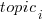 is the fraction of the
is the fraction of the 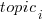 calculated to be present in the Summary text of the corresponding task.
calculated to be present in the Summary text of the corresponding task.
I’m please to see that a regression model can be improved by adding topics derived from the Summary text.
The SiP data includes other information such as work Category (e.g., development, management), ProjectCode and DeveloperId. It is to be expected that these factors will have some impact on the words appearing in a task Summary, and hence the topics (the stm analysis showed this effect for Category).
When the model formula is changed to: log(HoursActual) ~ log(HoursEstimate)+ProjectCode, the quality of fit for most topics became very poor. Is this because ProjectCode and topics conveyed very similar information, or did I need to be more sophisticated when extracting topic models? This needs further investigation.
Can topic models be used to build prediction models?
Summary text can only be used to make predictions if it is available before the event being predicted, e.g., available before a task is completed and the actual effort is known. My interest in model building is to understand the processes involved, so I am not worried about when the text was created.
My own habit is to update, or even create Summary text once a task is complete. I asked Stephen Cullen, my co-author on the original analysis and author of many of the Summary texts, about the process of creating the SiP Summary sentences. His reply was that the Summary field was an active document that was updated over time. I suspect the same is true for many task descriptions.
Not all estimation data includes as much information as the SiP dataset. If Summary text is one of the few pieces of information available, it may be possible to use it as a proxy for missing columns.
Perhaps it is possible to extract information from the SiP Summary text that is not also contained in the other recorded information. Having been successful this far, I will continue to investigate.
Another nail for the coffin of past effort estimation research
Programs are built from lines of code written by programmers. Lines of code played a starring role in many early effort estimation techniques (section 5.3.1 of my book). Why would anybody think that it was even possible to accurately estimate the number of lines of code needed to implement a library/program, let alone use it for estimating effort?
Until recently, say up to the early 1990s, there were lots of different computer systems, some with multiple (incompatible’ish) operating systems, almost non-existent selection of non-vendor supplied libraries/packages, and programs providing more-or-less the same functionality were written more-or-less from scratch by different people/teams. People knew people who had done it before, or even done it before themselves, so information on lines of code was available.
The numeric values for the parameters appearing in models were obtained by fitting data on recorded effort and lines needed to implement various programs (63 sets of values, one for each of the 63 programs in the case of COCOMO).
How accurate is estimated lines of code likely to be (this estimate will be plugged into a model fitted using actual lines of code)?
I’m not asking about the accuracy of effort estimates calculated using techniques based on lines of code; studies repeatedly show very poor accuracy.
There is data showing that different people implement the same functionality with programs containing a wide range of number of lines of code, e.g., the 3n+1 problem.
I recently discovered, tucked away in a dataset I had previously analyzed, developer estimates of the number of lines of code they expected to add/modify/delete to implement some functionality, along with the actuals.
The following plot shows estimated added+modified lines of code against actual, for 2,692 tasks. The fitted regression line, in red, is: 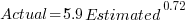 (the standard error on the exponent is
(the standard error on the exponent is 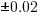 ), the green line shows
), the green line shows 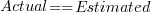 (code+data):
(code+data):
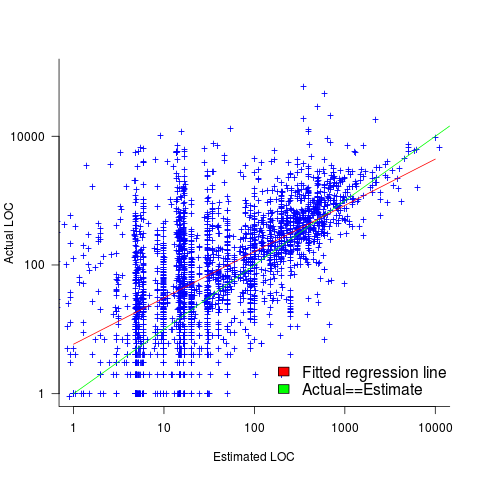
The fitted red line, for lines of code, shows the pattern commonly seen with effort estimation, i.e., underestimating small values and over estimating large values; but there is a much wider spread of actuals, and the cross-over point is much further up (if estimates below 50-lines are excluded, the exponent increases to 0.92, and the intercept decreases to 2, and the line shifts a bit.). The vertical river of actuals either side of the 10-LOC estimate looks very odd (estimating such small values happen when people estimate everything).
My article pointing out that software effort estimation is mostly fake research has been widely read (it appears in the first three results returned by a Google search on software fake research). The early researchers did some real research to build these models, but later researchers have been blindly following the early ‘prophets’ (i.e., later research is fake).
Lines of code probably does have an impact on effort, but estimating lines of code is a fool’s errand, and plugging estimates into models built from actuals is just crazy.
COCOMO: Not worth serious attention
The Constructive Cost Model (COCOMO) was introduced to the world by the book “Software Engineering Economics” by Barry Boehm; this particular version of the model is now known by the year of publication, COCOMO 81. The book describes a model that estimates software project cost drivers, such as effort (in man months) and elapsed time; the data from the 63 projects used to help calibrate the equations appears on pages 496-497.
Only having 63 measurements to model such a complex problem means any predictions will have very wide error bounds; however, the small amount of data did not stop Boehm building an academic career out of over-fitting these 63 measurements using 17 input parameters (the COCOMO II book came out in 2000 and was initially calibrated by fitting 22 parameters to 83 measurement points and then by fitting 23 parameters to 161 measurement points; the measurement data does not appear to be publicly available).
A sentence on page 493 suggests that over-fitting may not be the only problem to be found in the data analysis: “The calibration and evaluation of COCOMO has not relied heavily on advanced statistical techniques.”
Let’s take the original data and duplicate the original analysis, before trying something more advanced (code+data).
A central plank of the COCOMO model is the equation: 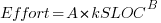 , where
, where 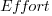 is total effort in man months,
is total effort in man months, 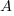 a constant obtained by fitting the data,
a constant obtained by fitting the data, 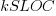 thousands of lines of source code and
thousands of lines of source code and 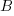 a constant obtained by fitting the data.
a constant obtained by fitting the data.
This post discusses fitting this equation for the three modes of software projects defined by Boehm (along with the equations he fitted):
- Organic, relatively small teams operating in a highly familiar environment:
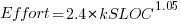 ,
, - Embedded, the product has to operate within strongly coupled, complex, hardware, software and operational procedures such as air traffic control:
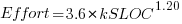 ,
, - Semidetached, an intermediate stage between the two extremes:
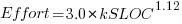 .
.
The plot below shows kSLOC against Effort, with solid lines fitted using what I guess was Boehm’s approach and dashed lines showing fitted lines after removing outliers (Figure 6-5 in the book has the x/y axis switched; the points in the above plot appear to match those in this figure):
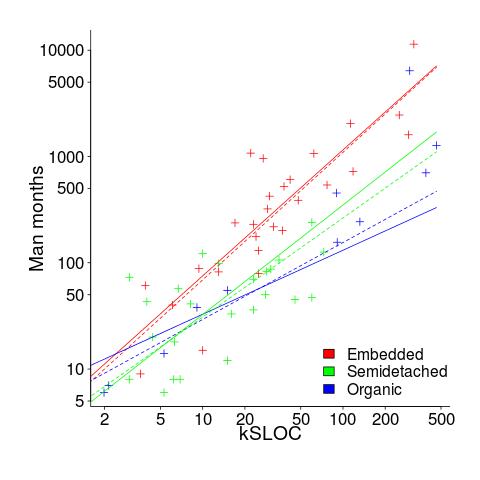
The fitted equations are (the standard error on the multiplier, 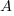 , is around ±30%, while on the exponent,
, is around ±30%, while on the exponent, 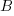 , the absolute value varies between ±0.1 and ±0.2):
, the absolute value varies between ±0.1 and ±0.2):
- Organic:
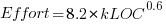 , after outlier removal
, after outlier removal 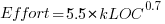
- Embedded:
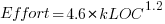 , after outlier removal
, after outlier removal 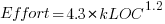
- Semidetached:
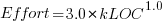 , after outlier removal
, after outlier removal 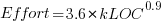 .
.
The only big difference is for Organic, which is very different. My first reaction on seeing this was to double check the values used against those in the book. How did Boehm make such a big mistake and why has nobody spotted it (or at least said anything) before now? Papers by Boehm’s students do use fancy statistical techniques and contain lots of tables of numbers relating to COCOMO 81, but no mention of what model they actually found to be a good fit.
The table on pages 496-497 contains man month estimates made using Boehm’s equations (the EST column). The values listed are a close match to the values I calculated using Boehm’s Semidetached equation, but there are many large discrepancies between printed values and values I calculated (using Boehm’s equations) for Organic and Embedded. If the data in this table contains a lot of mistakes, it may explain why I get very different values fitting the data for Organic. Some ther columns contain values calculated using the listed EST values and the few I have checked are correct, so if there was an error in the EST value calculation it must have occurred early in the chain of calculations.
The data for each of the three modes of software development contain several in your face outliers (assuming the values are correct). Based on the fitted equations is does not look like Boehm removed these (perhaps detecting outliers is an advanced technique).
Once the very obvious outliers are removed the quadratic equation, 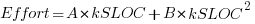 , becomes a viable competing model. Unfortunately we don’t have enough data to do a serious comparison of this equation against the COCOMO equation.
, becomes a viable competing model. Unfortunately we don’t have enough data to do a serious comparison of this equation against the COCOMO equation.
In practice the COCOMO 81 model has been found to be highly inaccurate and very much dependent upon the interpretation of the input parameters.
Further down on page 493 we have: “I have become convinced that the software field is currently too primitive, and cost driver interaction too complex, for standard statistical techniques to make much headway;”.
With so much complexity and uncertainty, careful application of statistical techniques is the only way of reliable way of distinguishing any signal from noise.
COCOMO does not deserve anymore serious attention (the code+data includes some attempts to build alternative models, before I decided it was not worth the effort).
Data cleaning: The next step in empirical software engineering
Over the last 10 years software engineering researchers have gone from a state of data famine to being deluged with data. Until recently these researchers have been acting like children at a birthday party, rushing around unwrapping all the presents to see what is inside and quickly moving onto the next one. A good example of this are those papers purporting to have found a power law relationship between two constructs by simply plotting the data using log axis and drawing a straight line through the data; hey look, a power law, isn’t that interesting? Hopefully, these days, reviewers are starting to wise up and insist that any claims of a power law be checked.
Data cleaning is a very important topic that unfortunately appears to be missing from many researchers’ approach to data analysis. The quality of a model built from data is only as good as the quality of the data used to build it. Anybody who is interested in building models that connect to the real world of software engineering, rather than just getting another paper published, has to consider the messiness that gets added to data by the software developers who are intimately involved in the processes that generated the artifacts (e.g., source code, bug reports).
I have jut been reading a paper containing some unsettling numbers (It’s not a Bug, it’s a Feature: On the Data Quality of Bug Databases). A manual classification of over 7,000 issues reported against various large Java applications found that 42.6% of the issues were misclassified (e.g., a fault report was actually a request for enhancement), resulting in a change of status of 39% of the files once thought to contain a fault to not actually containing a fault (any fault prediction models built assuming the data in the fault database was correct now belong in the waste bin).
What really caught my eye about this research was the 725 hours (90 working days) invested by the researchers doing the manual classification (one person + independent checking by another). Anybody can extracts counts of this that and the other from the many repositories now freely available, generate fancy looking plots from them and add in some technobabble to create a paper. Real researchers invest lots of their time figuring out what is really going on.
These numbers are a wakeup call for all software engineering researchers. The data you are using needs to be thoroughly checked and be prepared to invest a lot of time doing it.
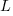 distinct local variables have been accessed for reading
distinct local variables have been accessed for reading 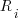 times (
times (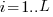 ), will the next read access be from a previously unread local variable and if not what is the likelihood of choosing each of the distinct
), will the next read access be from a previously unread local variable and if not what is the likelihood of choosing each of the distinct 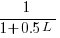 select a new variable to access,
select a new variable to access, 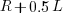 (where
(where 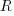 is the number of times the variable has previously been read from.
is the number of times the variable has previously been read from.  read accesses to locally defined variables, how many variables will be read from only once, how many twice and so on (this is a static count extracted from the source code, not a dynamic count obtained by executing the function)?
read accesses to locally defined variables, how many variables will be read from only once, how many twice and so on (this is a static count extracted from the source code, not a dynamic count obtained by executing the function)?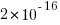 ; see rexample[local-use]):
; see rexample[local-use]):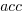 is the number of read accesses to a given variable and
is the number of read accesses to a given variable and 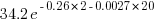 .
. select a new web page (in this case a new variable to access),
select a new web page (in this case a new variable to access),  select an existing web page (a variable that has previously been accessed in the function), select a variable with a probability proportional to the number of times it has previously been accessed (i.e., a variable that has four previous read accesses is twice as likely to be chosen as one that has had two previous accesses).
select an existing web page (a variable that has previously been accessed in the function), select a variable with a probability proportional to the number of times it has previously been accessed (i.e., a variable that has four previous read accesses is twice as likely to be chosen as one that has had two previous accesses). 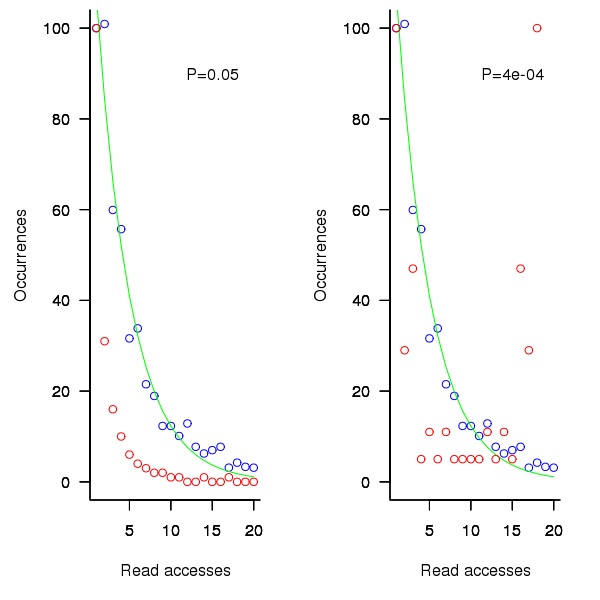
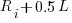 (where
(where 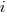 so far) produces behavior that matches the data to the same degree as the exponential model.
so far) produces behavior that matches the data to the same degree as the exponential model.
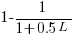 select a variable that has previously been accessed in the function, select an existing variable with probability proportional to
select a variable that has previously been accessed in the function, select an existing variable with probability proportional to 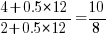 times as likely to be chosen as one that has had two previous accesses).
times as likely to be chosen as one that has had two previous accesses).
Recent Comments