Archive
Indented vs non-indented if-statements: performance difference
To non-developers discussions about the visual layout of source code can seem somewhat inconsequential. Layout probably ought to be inconsequential, being based on experimental studies that discovered how source should be visually organised to minimise the cognitive effort consumed by developers while processing it.
In practice software engineering is not evidence-based. There are two kinds of developers: those willing to defend to the death the layout they use, and those that have moved on.
In its simplest form visual layout involves indenting code some number of spaces from the left margin. Use of indentation has not always been widespread, and people wrote papers extolling the readability benefits of indenting code.
My experience with talking to developers about indentation is that they are heavily influenced by the indentation practices adopted by those around them when first learning a language. Layout habits from any prior language tend to last awhile, depending on the amount of time spent with the prior language.
As far as I know, I have had zero success arguing that the Gestalt principles of perception provide a useful framework for deciding between different code layouts.
The layout issue that attracts the most discussion is probably the indentation of if-statements. What, if any, is the evidence around this issue?
Developer indentation discussions focus on which indentation is better than the alternatives (whatever better might be). A more salient question would be the size of the developer performance difference, or is the difference large enough to care about?
Researchers have used several techniques for measuring difference in developer performance, including: code comprehension (i.e., number of correct answers to questions about the code they have just read), subjective ratings (i.e., how hard did the subjects find the task), and time to complete a task (e.g., modify source, find coding mistake).
The subjects have invariably been a small sample of undergraduates studying for a computing degree, so the usual caveats about applicability to professional developers apply.
Until 2023, the most detailed work I know of is a PhD thesis from 1974 studying the impact of mnemonic/meaningless variable names plus none/some indentation (experiments 1, 2 and 9), and a 1983 paper which compared subject performance with indentation of none and 2/4/6 spaces (contains summary data only). Both studies used small programs.
The 2023 paper Indentation in Source Code: A Randomized Control Trial on the Readability of Control Flows in Java Code with Large Effects by J. Morzeck, S. Hanenberg, O. Werger, and V. Gruhn measured the time taken by 20 subjects to answer 12 questions about the value printed by a randomly generated program containing a nested if-statement. The following shows an example without/with indentation (values were provided for i and j):
if (i != j) { if (i != j) { if (j > 10) { if (j > 10) { if (i < 10) { if (i < 10) { print (5); print (5); } else { } else { print (10); print (10); } } } else { } else { print (12); print (12); } } } else { } else { if (i < 10) { if (i < 10) { print (23); print (23); } else { } else { print (15); print (15); } } } } |
A fitted regression model found that the average response time of 122 seconds (yes, very slow) for non-indented code decreased to 44 seconds (not quite as slow) for indented code, i.e., about three times faster (code+data). This huge performance improvement is very different from most software engineering experiments where the largest effect is the between subjects performance, with learning producing the next largest effect.
Evidence that indentation is very effective, but nobody doubted this. There has been a follow-up study, more on that another time.
if statement conditions, some basic measurements
The conditions contained in if-statements control all the decisions a program makes, yet relatively little is known about their characteristics.
A condition contains one or more clauses, for instance, the condition (a && b) contains two clauses that both need to be true, for the condition to be true. An earlier post modelled the number of clauses in Java conditions, and found an exponential decline (around 90% of conditions contained a single clause, for C this is around 85%).
The condition in a nested if-statement contains implicit decisions, because its evaluation depends on the conditions evaluated by its outer if-statements. I have long predicted that, on average, the number of clauses in a condition will decrease as if-statement nesting increases, because some decisions are subsumed by outer conditions. I have not seen any measurements on conditionals vs nesting, and this week this question reached the top of my to-do list.
I used Coccinelle to extract the text contained in each condition, along with the start/end line numbers of the associated if/else compound statement(s). After almost 20 years, Coccinelle is still the most flexible C source analysis tool available that does not require delving into compiler internals. The following is an example of the output (code and data):
file;stmt;if_line;if_col;cmpd_end;cmpd_line_end;expr sqlite-src-3460100/src/fkey.c;if;240;10;240;243;aiCol sqlite-src-3460100/src/fkey.c;if;217;6;217;217;! zKey sqlite-src-3460100/src/fkey.c;if;275;8;275;275;i == nCol sqlite-src-3460100/src/fkey.c;if;1428;6;1428;1433;aChange == 0 || fkParentIsModified ( pTab , pFKey , aChange , bChngRowid ) sqlite-src-3460100/src/fkey.c;if;808;4;808;808;iChildKey == pTab -> iPKey && bChngRowid sqlite-src-3460100/src/fkey.c;if;452;4;452;454;nIncr > 0 && pFKey -> isDeferred == 0 |
The conditional expressions (last column above) were reduced to a basic form involving simple variables and logical operators, along with operator counts. Some example output below (code and data):
simp_expr,land,lor,ternary v1,0,0,0 v1 && v2,1,0,0 v1 || v2,0,1,0 v1 && v2 && v3,2,0,0 v1 || ( v2 && v3 ),1,1,0 ( v1 && v2 ) || ( v3 && v4 ),2,1,0 ( v1 ? dm1 : dm2 ),0,0,1 |
The C source code projects measured were the latest stable versions of Vim (44,205 if-statements), SQLite (27,556 if-statements), and the Linux kernel (version 6.11.1; 1,446,872 if-statements).
A side note: I was surprised to see the ternary operator appearing in some conditions; in effect, an if within an if (see last line of the previous example). The ternary operator usually appears as a component of a large conditional expression (e.g., x + ( v1 ? dm1 : dm2 ) > y), rather than itself containing clauses, e.g., ( v1 ? dm1 : dm2 ) && v2. I have not seen the requirements for this operator discussed in any analysis of MC/DC.
The plot below shows the number of if-statements occurring at a given nesting level, along with regression fits, of the form 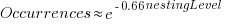 , to the Vim and SQLite data; the Linux data was better fit by a power law (code+data):
, to the Vim and SQLite data; the Linux data was better fit by a power law (code+data):
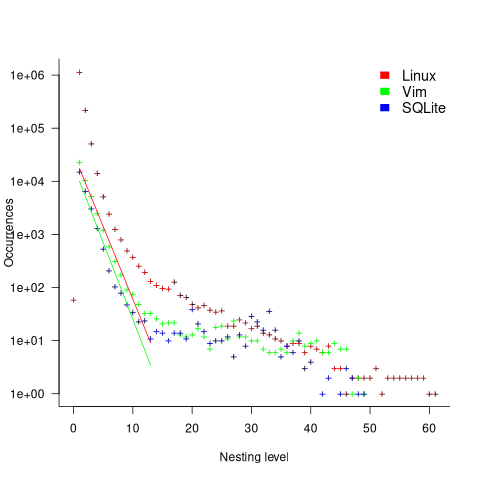
I suspect that most of the deeply nested levels in Vim and SQLite are the results of long else if chains, which, while technically highly nested, could all have been written having the same nesting level, such as the following:
if (strcmp(x, "abc")) ; // code else if (strcmp(x, "xyz")) ; // code else if (strcmp(x, "123")) ; // code |
This if else pattern does not appear to be common in Linux. Perhaps ‘regularizing’ the if else sequences in Vim and SQLite will move the distribution towards a power law (i.e., like Linux).
Average nesting depth will also be affected by the average number of lines per function, with functions containing more statements providing the opportunity for more deeply nested if-statements (rather than calling a function containing nested if-statements).
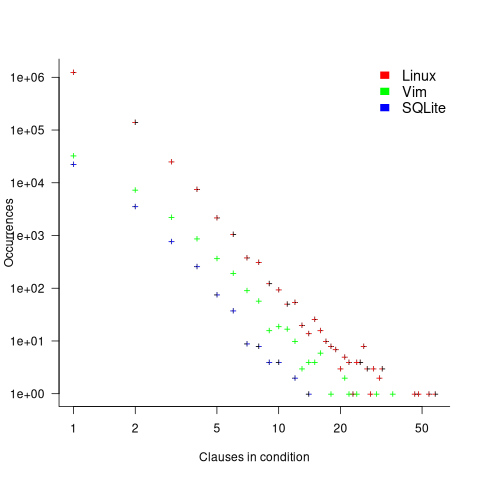
The plot below shows the number of occurrences of conditions containing a given number of clauses. Neither the exponential and power law are good fits, and log-log axis are used because it shows the points are closer to forming a straight line (code+data):
The plot below shows the nesting level and number of clauses in the condition for each of the 1,446,872 if-statements in the Linux kernel. Each value was ‘jittered’ to distribute points about their actual value, creating a more informative visualization (code+data):
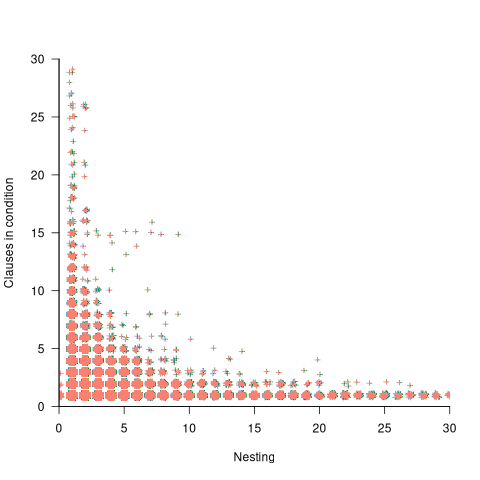
As expected, the likelihood of a condition containing multiple clauses does decrease with nesting level. However, with around 85% of conditions containing a single clause, the fitted regression models essential predict one clause for all nesting levels.
Number of statement sequences possible using N if-statements
I recently read a post by Terence Tao describing how he experimented with using ChatGPT to solve a challenging mathematical problem. A few of my posts contain mathematical problems I could not solve; I assumed that solving them was beyond my maths pay grade. Perhaps ChatGPT could help me solve some of them.
To my surprise, a solution was found to the first problem I tried.
I simplified the original problem (involving Motzkin numbers, details below) down to something that was easier for me to explain to ChatGPT. Based on ChatGPT’s response, it appeared lost, so I asked what it knew about Motzkin numbers. I then reframed the question around the concepts in its response, and got a response that, while reasonable, was not a solution. My question was not precise enough, and a couple of question/answer iterations later, ChatGPT broke the problem down into a series of steps that I saw could solve the problem. While the equation it used in its answer was just wrong, I knew what the correct equation was. So while ChatGPT frequently went off in the wrong direction and got its maths wrong, it helped me refine my statement of the problem and ChatGPT eventually gave steps to a solution which were blindingly obvious to me when I read them.
The question I wanted to answer was: How many distinct statement sequences can be created using 
if-statements and  simple-statements (for a total of
simple-statements (for a total of  statements)?
statements)?
A simple-statement might be an assignment or function call, but not any kind of compound statement, such as a loop. Three sequences are possible using one if-statement and two simple-statements. The if-statement occupies two lines, i.e., the condition and termination curly-bracket, }, as follows:
s1; if (c1) { if (c1) { if (c1) { s1; s1; s2; s2; } } } s2; |
In a previous post I showed how a variant of this question, involving any number of if-statements, can be mapped to a combinatorial interpretation of Motzkin numbers and treating matching up/down diagonals along a path as an if-statement.

ChatGPT performed poorly when I phrased the problem in combinatorial terms (or perhaps my phrasing was poor), so I switched to using a lattice path approach. I asked: “How many lattice paths of length S containing exactly N occurrences of the step (1, 1) and N occurrences of the step (1, -1) are possible?”, and after reading the response I replied “Your analysis does not take into account the fact that the path cannot go below the x-axis. Rework your analysis to take this restriction into account.”
The following is my edited version of ChatGPT’s ‘solution’ response:
“Problem Restated:
We need to count the number of valid Dyck paths of length  , where the path consists of:
, where the path consists of:
Exactly  upward steps (1,1).
upward steps (1,1).
Exactly  downward steps (1,−1).
downward steps (1,−1).
The remaining steps (which must be  horizontal steps (1,0)).
horizontal steps (1,0)).
These paths must never dip below the x-axis, and they must return to the x-axis at the end.
…
Step 2: Catalan Numbers for Balanced Paths
If we ignore the horizontal steps for the moment, the number of ways to place  upward steps and
upward steps and  downward steps such that the path does not go below the x-axis is given by the Catalan number
downward steps such that the path does not go below the x-axis is given by the Catalan number 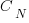 :
:
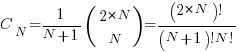
This Catalan number counts the number of valid ways to arrange the  upward steps and
upward steps and  downward steps such that the path remains above or on the x-axis.
downward steps such that the path remains above or on the x-axis.
Step 3: Placing Horizontal Steps
Once the valid upward and downward steps have been arranged in a Catalan structure, we can freely place the  horizontal steps (1,0) in the remaining positions of the path. Since there are
horizontal steps (1,0) in the remaining positions of the path. Since there are 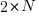 steps (upward and downward) and
steps (upward and downward) and  horizontal steps, there are
horizontal steps, there are 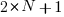 gaps (before, after, or between the upward/downward steps) where the horizontal steps can be placed.
gaps (before, after, or between the upward/downward steps) where the horizontal steps can be placed.
The number of ways to place  horizontal steps in these
horizontal steps in these 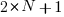 positions is given by a binomial coefficient:”
positions is given by a binomial coefficient:”
For some reason, ChatGPT gives the wrong binomial coefficient. Calculating the number of ways of distributing 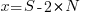 items into
items into 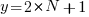 bins is a well known problem; when a bin can contain zero items, the solution is:
bins is a well known problem; when a bin can contain zero items, the solution is: 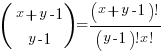 .
.
Combining the equations from the two steps gives the number of distinct statement sequences that can be created using 
if-statements and  simple-statements as:
simple-statements as:
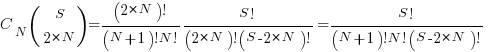
The above answer is technically correct, however, it fails to take into account that in practice an if-statement body will always contain either another if-statement or a simple statement, i.e., the innermost if-statement of any nested sequence cannot be empty (the equation used for distributing items into bins assumes a bin can be empty).
Rather than distributing  statements into
statements into 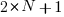 gaps, we first need to insert one simple statement into each of the innermost if-statements. The number of ways of distributing the remaining statements are then counted as previously. How many innermost if-statements can be created using
gaps, we first need to insert one simple statement into each of the innermost if-statements. The number of ways of distributing the remaining statements are then counted as previously. How many innermost if-statements can be created using  if-statements? I found the answer to this question in a StackExchange question, using traditional search.
if-statements? I found the answer to this question in a StackExchange question, using traditional search.
The question can be phrased in terms of peaks in Dyck paths, and the answer is contained in the Narayana numbers (which I had never heard of before). The following example, from Wikipedia, shows the number of paths containing a given number of peaks, that can be produced by four if-statements:
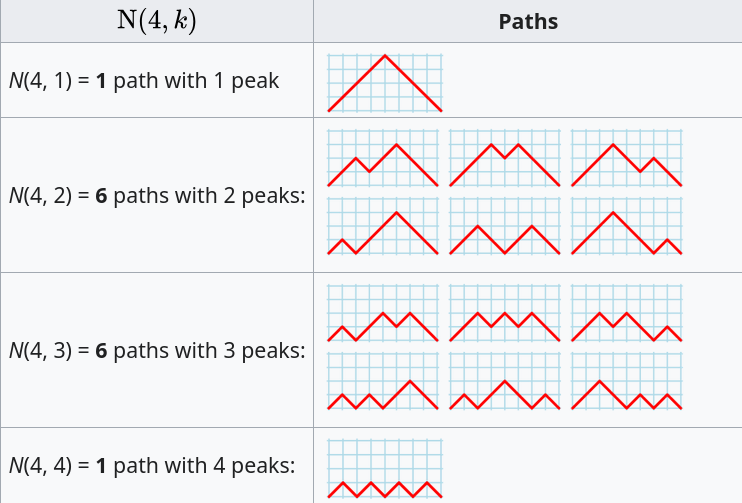
The sum of all these paths is the Catalan number for the given number of if-statements, e.g., using 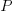 to denote the Narayana number:
to denote the Narayana number: 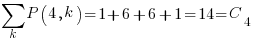 .
.
Adding at least one simple statement to each innermost if-statement changes the equation for the number of statement sequences from 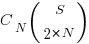 , to:
, to:
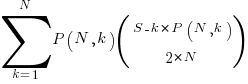
The following table shows the number of distinct statement sequences for five-to-twenty statements containing one-to-five if-statements:
N if-statements
1 2 3 4 5
5 6 1
6 10 6
7 15 20 1
8 21 50 7
9 28 105 29 1
10 36 196 91 9
11 45 336 238 45 1
12 55 540 549 166 11
S 13 66 825 1,155 504 66
14 78 1,210 2,262 1,332 286
15 91 1,716 4,179 3,168 1,002
16 105 2,366 7,351 6,930 3,014
17 120 3,185 12,397 14,157 8,074
18 136 4,200 20,153 27,313 19,734
19 153 5,440 31,720 50,193 44,759
20 171 6,936 48,517 88,458 95,381 |
The following is an R implementation of the calculation:
Narayana=function(n, k) choose(n, k)*choose(n, k-1)/n
Catalan=function(n) choose(2*n, n)/(n+1)
if_stmt_possible=function(S, N)
{
return(Catalan(N)*choose(S, 2*N)) # allow empty innermost if-statement
}
if_stmt_cnt=function(S, N)
{
if (S <= 2*N)
return(0)
total=0
for (k in 1:N)
{
P=Narayana(N, k)
if (S-P*k >= 2*N)
total=total+P*choose(S-P*k, 2*N)
}
return(total)
}
isc=matrix(nrow=25, ncol=5)
for (S in 5:20)
for (N in 1:5)
isc[S, N]=if_stmt_cnt(S, N)
print(isc) |
Research ideas for 2023/2024
Students sometimes ask me for suggestions of interesting research problems in software engineering. A summary of my two recurring suggestions, for this year, appears below; 2016/2017 and 2019/2020 versions.
How many active users does a program or application have?
The greater the number of users, the greater the number of reported faults. Estimates of program reliability have to include volume of usage as an integral part of the calculation.
Non-trivial amounts of public data on program usage is non-existent (in a few commercial environments, users are charged for using software on a per-usage basis, but this data is confidential). Usage has to be estimated by indirect means.
A popular indirect technique for estimating the popularity of Github repos is to count the number of stars it has; however, stars have a variety of interpretations. The extent to which Github stars tracks usage of the repo’s software is not known.
Other indirect techniques include: web server logs, installs of the application, or the operating system.
One technique that has not yet been researched is to make use of the identity of those reporting faults. A parallel can be drawn with the fish population in lakes, which is not directly visible. Ecologists have developed techniques for indirectly estimating the population size of distinct creatures using information about a subset of the population, and some of the population models developed for ecology can be adapted to estimating program user populations.
Estimates of population size can be obtained by plugging information on the number of different people reporting faults, and the number of reports from the same person into these models. This approach is not as easy as it sounds because sometimes the same person has multiple identities, reported faults also need to be deduplicated and cleaned (30-40% of reports have been found to be requests for enhancements).
Nested if-statement execution
As if-statement nesting depth increases, the number of conditions controlling the execution of the enclosed code increases.
Being able to estimate the likelihood of executing the code controlled by an if-statement is of interest to: compilers wanting to target optimizations along the most frequently executed paths, special handling for error paths, testing along the least/most likely paths (e.g., fuzzers wanting to know the conditions needed to reach a given block), those wanting to organize code for ease of understanding, by reducing cognitive effort to understand.
Possible techniques for analysing the likelihood of executing code controlled by one or more nested if-statements include:
- Compiler writers have discovered various heuristics for predicting the likely outcome of a branch, and there are probably more to be discovered. Statement coverage counts provides a ground truth against which to compare ideas,
- analysis of the conditional expression,
- mathematical analysis of the distribution of values of variables in conditional expressions.
Focus of activities planned for 2023
In 2023, my approach to evidence-based software engineering pivots away from past years, which were about maximizing the amount of software engineering data gathered.
I plan to spend a lot more time attempting to join dots (i.e., finding useful patterns in the available data), and I also plan to spend time collecting my own data (rather than other peoples’ data).
I will continue to keep asking people for data, and I’m sure that new data will become available (and be the subject of blog posts). The amount of previously unseen data obtained by continuing to read pre-2020 papers is likely to be very small, and not worth targetting. Post-2020 papers will be the focus of my search for new data (mostly conference proceedings and arXiv’s software engineering recent submissions)
It would be great if there was an active community of evidence-based developers. The problem is that the people with the necessary skills are busily employed building real systems. I’m hopeful that people with the appropriate background and skills will come out of the woodwork.
Ideally, I would be running experiments with developer subjects; this is the only reliable way to verify theories of software engineering. While it’s possible to run small scale experiments with developer volunteers, running a workplace scale experiment will be expensive (several million pounds/dollars). I don’t move in the circles frequented by the very wealthy individuals who might fund such an experiment. So this is a back-burner project.
if-statements continue to be of great interest to me; they represent decisions that relate to requirements and tests that need to be written. I used to spend a lot of time measuring, mostly C, source code: how the same variable is tested in nested conditions, the use of else arms, and the structuring of conditions within a function. The availability of semgrep will, hopefully, enable me to measure various aspect of if-statement usage across different languages.
I hope that my readers continue to keep their eyes open for interesting software engineering data, and will let me know when they find any.
semgrep: the future of static analysis tools
When searching for a pattern that might be present in source code contained in multiple files, what is the best tool to use?
The obvious answer is grep, and grep is great for character-based pattern searches. But patterns that are token based, or include information on language semantics, fall outside grep‘s model of pattern recognition (which does not stop people trying to cobble something together, perhaps with the help of complicated sed scripts).
Those searching source code written in C have the luxury of being able to use Coccinelle, an industrial strength C language aware pattern matching tool. It is widely used by the Linux kernel maintainers and people researching complicated source code patterns.
Over the 15+ years that Coccinelle has been available, there has been a lot of talk about supporting other languages, but nothing ever materialized.
About six months ago, I noticed semgrep and thought it interesting enough to add to my list of tool bookmarks. Then, a few days ago, I read a brief blog post that was interesting enough for me to check out other posts at that site, and this one by Yoann Padioleau really caught my attention. Yoann worked on Coccinelle, and we had an interesting email exchange some 13-years ago, when I was analyzing if-statement usage, and had subsequently worked on various static analysis tools, and was now working on semgrep. Most static analysis tools are created by somebody spending a year or so working on the implementation, making all the usual mistakes, before abandoning it to go off and do other things. High quality tools come from people with experience, who have invested lots of time learning their trade.
The documentation contains lots of examples, and working on the assumption that things would be a lot like using Coccinelle, I jumped straight in.
The pattern I choose to search for, using semgrep, involved counting the number of clauses contained in Python if-statement conditionals, e.g., the condition in: if a==1 and b==2: contains two clauses (i.e., a==1, b==2). My interest in this usage comes from ideas about if-statement nesting depth and clause complexity. The intended use case of semgrep is security researchers checking for vulnerabilities in code, but I’m sure those developing it are happy for source code researchers to use it.
As always, I first tried building the source on the Github repo, (note: the Makefile expects a git clone install, not an unzipped directory), but got fed up with having to incrementally discover and install lots of dependencies (like Coccinelle, the code is written on OCaml {93k+ lines} and Python {13k+ lines}). I joined the unwashed masses and used pip install.
The pattern rules have a yaml structure, specifying the rule name, language(s), message to output when a match is found, and the pattern to search for.
After sorting out various finger problems, writing C rather than Python, and misunderstanding the semgrep output (some of which feels like internal developer output, rather than tool user developer output), I had a set of working patterns.
The following two patterns match if-statements containing a single clause (if.subexpr-1), and two clauses (if.subexpr-2). The option commutative_boolop is set to true to allow the matching process to treat Python’s or/and as commutative, which they are not, but it reduces the number of rules that need to be written to handle all the cases when ordering of these operators is not relevant (rules+test).
rules: - id: if.subexpr-1 languages: [python] message: if-cond1 patterns: - pattern: | if $COND1: # we found an if statement $BODY - pattern-not: | if $COND2 or $COND3: # must not contain more than one condition $BODY - pattern-not: | if $COND2 and $COND3: $BODY severity: INFO - id: if.subexpr-2 languages: [python] options: commutative_boolop: true # Reduce combinatorial explosion of rules message: if-cond2 pattern-either: - patterns: - pattern: | if $COND1 or $COND2: # if statement containing two conditions $BODY - pattern-not: | if $COND3 or $COND4 or $COND5: # must not contain more than two conditions $BODY - pattern-not: | if $COND3 or $COND4 and $COND5: $BODY - patterns: - pattern: | if $COND1 and $COND2: $BODY - pattern-not: | if $COND3 and $COND4 and $COND5: $BODY - pattern-not: | if $COND3 and $COND4 or $COND5: $BODY severity: INFO |
The rules would be simpler if it were possible for a pattern to not be applied to code that earlier matched another pattern (in my example, one containing more clauses). This functionality is supported by Coccinelle, and I’m sure it will eventually appear in semgrep.
This tool has lots of rough edges, and is still rapidly evolving, I’m using version 0.82, released four days ago. What’s exciting is the support for multiple languages (ten are listed, with experimental support for twelve more, and three in beta). Roughly what happens is that source code is mapped to an abstract syntax tree that is common to all supported languages, which is then pattern matched. Supporting a new language involves writing code to perform the mapping to this common AST.
It’s not too difficult to map different languages to a common AST that contains just tokens, e.g., identifiers and their spelling, literals and their value, and keywords. Many languages use the same operator precedence and associativity as C, plus their own extras, and they tend to share the same kinds of statements; however, declarations can be very diverse, which makes life difficult for supporting a generic AST.
An awful lot of useful things can be done with a tool that is aware of expression/statement syntax and matches at the token level. More refined semantic information (e.g., a variable’s type) can be added in later versions. The extent to which an investment is made to support the various subtleties of a particular language will depend on its economic importance to those involved in supporting semgrep (Return to Corp is a VC backed company).
Outside of a few languages that have established tools doing deep semantic analysis (i.e., C and C++), semgrep has the potential to become the go-to static analysis tool for source code. It will benefit from the network effects of contributions from lots of people each working in one or more languages, taking their semgrep skills and rules from one project to another (with source code language ceasing to be a major issue). Developers using niche languages with poor or no static analysis tool support will add semgrep support for their language because it will be the lowest cost path to accessing an industrial strength tool.
How are the VC backers going to make money from funding the semgrep team? The traditional financial exit for static analysis companies is selling to a much larger company. Why would a large company buy them, when they could just fork the code (other company sales have involved closed-source tools)? Perhaps those involved think they can make money by selling services (assuming semgrep becomes the go-to tool). I have a terrible track record for making business predictions, so I will stick to the technical stuff.
Update
Parts of the semgrep source have changed from an Open source license to a commercial one.
Opengrep is an Open source fork of semgrep.
Impact of function size on number of reported faults
Are longer functions more likely to contain more coding mistakes than shorter functions?
Well, yes. Longer functions contain more code, and the more code developers write the more mistakes they are likely to make.
But wait, the evidence shows that most reported faults occur in short functions.
This is true, at least in Java. It is also true that most of a Java program’s code appears in short methods (in C 50% of the code is contained in functions containing 114 or fewer lines, while in Java 50% of code is contained in methods containing 4 or fewer lines). It is to be expected that most reported faults appear in short functions. The plot below shows, left: the percentage of code contained in functions/methods containing a given number of lines, and right: the cumulative percentage of lines contained in functions/methods containing less than a given number of lines (code+data):
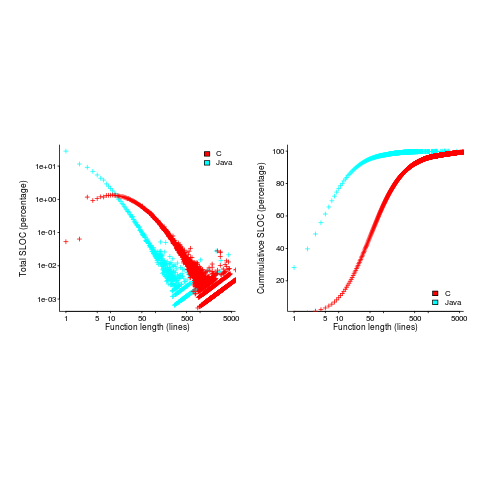
Does percentage of program source really explain all those reported faults in short methods/functions? Or are shorter functions more likely to contain more coding mistakes per line of code, than longer functions?
Reported faults per line of code is often referred to as: defect density.
If defect density was independent of function length, the plot of reported faults against function length (in lines of code) would be horizontal; red line below. If every function contained the same number of reported faults, the plotted line would have the form of the blue line below.
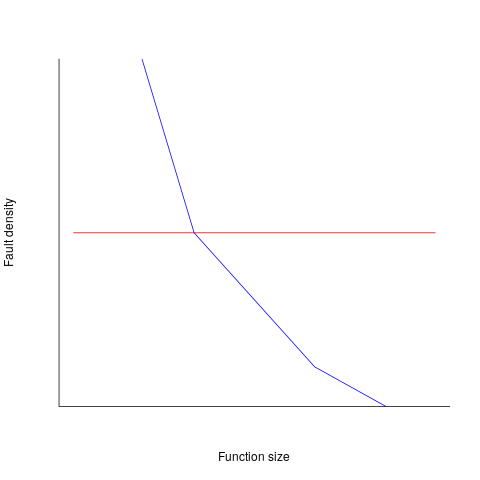
Two things need to occur for a fault to be experienced. A mistake has to appear in the code, and the code has to be executed with the ‘right’ input values.
Code that is never executed will never result in any fault reports.
In a function containing 100 lines of executable source code, say, 30 lines are rarely executed, they will not contribute as much to the final total number of reported faults as the other 70 lines.
How does the average percentage of executed LOC, in a function, vary with its length? I have been rummaging around looking for data to help answer this question, but so far without any luck (the llvm code coverage report is over all tests, rather than per test case). Pointers to such data very welcome.
Statement execution is controlled by if-statements, and around 17% of C source statements are if-statements. For functions containing between 1 and 10 executable statements, the percentage that don’t contain an if-statement is expected to be, respectively: 83, 69, 57, 47, 39, 33, 27, 23, 19, 16. Statements contained in shorter functions are more likely to be executed, providing more opportunities for any mistakes they contain to be triggered, generating a fault experience.
Longer functions contain more dependencies between the statements within the body, than shorter functions (I don’t have any data showing how much more). Dependencies create opportunities for making mistakes (there is data showing dependencies between files and classes is a source of mistakes).
The previous analysis makes a large assumption, that the mistake generating a fault experience is contained in one function. This is true for 70% of reported faults (in AspectJ).
What is the distribution of reported faults against function/method size? I don’t have this data (pointers to such data very welcome).
The plot below shows number of reported faults in C++ classes (not methods) containing a given number of lines (from a paper by Koru, Eman and Mathew; code+data):
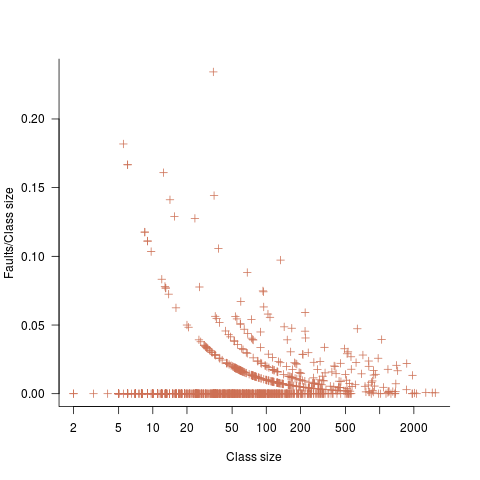
It’s tempting to think that those three curved lines are each classes containing the same number of methods.
What is the conclusion? There is one good reason why shorter functions should have more reported faults, and another good’ish reason why longer functions should have more reported faults. Perhaps length is not important. We need more data before an answer is possible.
How should involved if-statement conditionals be structured?
Which of the following two if-statements do you think will be processed by readers in less time, and with fewer errors, when given the value of x, and asked to specify the output?
// First - sequence of subexpressions if (x > 0 && x < 10 || x > 20 && x < 30) print("a"); else print "b"); // Second - nested ifs if (x > 0 && x < 10) print("c"); else if (x > 20 && x < 30) print("d"); else print("e"); |
Ok, the behavior is not identical, in that the else if-arm produces different output than the preceding if-arm.
The paper Syntax, Predicates, Idioms — What Really Affects Code Complexity? analyses the results of an experiment that asked this question, including more deeply nested if-statements, the use of negation, and some for-statement questions (this post only considers the number of conditions/depth of nesting components). A total of 1,583 questions were answered by 220 professional developers, with 415 incorrect answers.
Based on the coefficients of regression models fitted to the results, subjects processed the nested form both faster and with fewer incorrect answers (code+data). As expected performance got slower, and more incorrect answers given, as the number of intervals in the if-condition increased (up to four in this experiment).
I think short-term memory is involved in this difference in performance; or at least I can concoct a theory that involves a capacity limited memory. Comprehending an expression (such as the conditional in an if-statement) requires maintaining information about the various components of the expression in working memory. When the first subexpression of x > 0 && x < 10 || x > 20 && x < 30 is false, and the subexpression after the || is processed, there is no now forget-what-went-before point like there is for the nested if-statements. I think that the single expression form is consuming more working memory than the nested form.
Does the result of this experiment (assuming it is replicated) mean that developers should be recommended to write sequences of conditions (e.g., the first if-statement example) about as:
if (x > 0 && x < 10) print("a"); else if (x > 20 && x < 30) print("a"); else print("b"); |
Duplicating code is not good, because both arms have to be kept in sync; ok, a function could be created, but this is extra effort. As other factors are taken into account, the costs of the nested form start to build up, is the benefit really worth the cost?
Answering this question is likely to need a lot of work, and it would be a more efficient use of resources to address questions about more commonly occurring conditions first.
A commonly occurring use is testing a single range; some of the ways of writing the range test include:
if (x > 0 && x < 10) ... if (0 < x && x < 10) ... if (10 > x && x > 0) ... if (x > 0 && 10 > x) ... |
Does one way of testing the range require less effort for readers to comprehend, and be more likely to be interpreted correctly?
There have been some experiments showing that people are more likely to give correct answers to questions involving information expressed as linear syllogisms, if the extremes are at the start/end of the sequence, such as in the following:
A is better than B
B is better than C |
and not the following (which got the lowest percentage of correct answers):
B is better than C
B is worse than A |
Your author ran an experiment to find out whether developers were more likely to give correct answers for particular forms of range tests in if-conditions.
Out of a total of 844 answers, 40 were answered incorrectly (roughly one per subject; it was a paper and pencil experiment, so no timings). It's good to see that the subjects were so competent, but with so few mistakes made the error bars are very wide, i.e., too few mistakes were made to be able to say that one representation was less mistake-prone than another.
I hope this post has got other researchers interested in understanding developer performance, when processing if-statements, and that they will be running more experiments help shed light on the processes involved.
Motzkin paths and source code silhouettes
Consider a language that just contains assignments and if-statements (no else arm). Nesting level could be used to visualize programs written in such a language; an if represented by an Up step, an assignment by a Level step, and the if-terminator (e.g., the } token) by a Down step. Silhouettes for the nine possible four line programs are shown in the figure below (image courtesy of Wikipedia). I use the term silhouette because the obvious terms (e.g., path and trace) have other common usage meanings.

How many silhouettes are possible, for a function containing 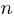 statements? Motzkin numbers provide the answer; the number of silhouettes for functions containing from zero to 20 statements is: 1, 1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019. The recurrence relation for Motzkin numbers is (where
statements? Motzkin numbers provide the answer; the number of silhouettes for functions containing from zero to 20 statements is: 1, 1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019. The recurrence relation for Motzkin numbers is (where 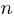 is the total number of steps, i.e., statements):
is the total number of steps, i.e., statements):
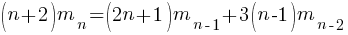
Human written code contains recurring patterns; the probability of encountering an if-statement, when reading code, is around 17% (at least for the C source of some desktop applications). What does an upward probability of 17% do to the Motzkin recurrence relation? For many years, I have been keeping my eyes open for possible answers (solving the number theory involved is well above my mathematics pay grade). A few days ago, I discovered weighted Motzkin paths.
A weighted Motzkin path is one where the Up, Level and Down steps each have distinct weights. The recurrence relationship for weighted Motzkin paths is expressed in terms of number of colored steps, where: 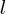 is the number of possible colors for the Level steps, and
is the number of possible colors for the Level steps, and 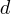 is the number of possible colors for Down steps; Up steps are assumed to have a single color:
is the number of possible colors for Down steps; Up steps are assumed to have a single color:
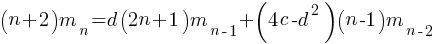
setting: 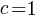 and
and 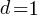 (i.e., all kinds of step have one color) recovers the original relation.
(i.e., all kinds of step have one color) recovers the original relation.
The different colored Level steps might be interpreted as different kinds of non-nesting statement sequences, and the different colored Down steps might be interpreted as different ways of decreasing nesting by one (e.g., a goto statement).
The connection between weighted Motzkin paths and probability is that the colors can be treated as weights that add up to 1. Searching on “weighted Motzkin” returns the kind of information I had been looking for; it seems that researchers in other fields had already discovered weighted Motzkin paths, and produced some interesting results.
If an automatic source code generator outputs the start of an if statement (i.e., an Up step) with probability 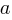 , an assignment (i.e., a Level step) with probability
, an assignment (i.e., a Level step) with probability 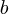 , and terminates the
, and terminates the if (i.e., a Down step) with probability 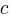 , what is the probability that the function will contain at least
, what is the probability that the function will contain at least 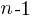 statements? The answer, courtesy of applying Motzkin paths in research into clone cell distributions, is:
statements? The answer, courtesy of applying Motzkin paths in research into clone cell distributions, is:
![P_n=sum{i=0}{delim{[}{(n-2)/2}{]}}(matrix{2}{1}{{n-2} {2i}})C_{2i}a^{i}b^{n-2-2i}c^{i+1} P_n=sum{i=0}{delim{[}{(n-2)/2}{]}}(matrix{2}{1}{{n-2} {2i}})C_{2i}a^{i}b^{n-2-2i}c^{i+1}](https://shape-of-code.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_960.5_57086dac25a2ff31c2230f0791800e35.png)
where: 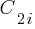 is the
is the 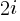 ‘th Catalan number, and that
‘th Catalan number, and that [...] is a truncation; code for an implementation in R.
In human written code we know that 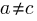 , because the number of statements in a compound-statement roughly has an exponential distribution (at least in C).
, because the number of statements in a compound-statement roughly has an exponential distribution (at least in C).
There has been some work looking at the number of peaks in a Motzkin path, with one formula for the total number of peaks in all Motzkin paths of length n. A formula for the number of paths of length 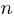 , having
, having 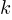 peaks, would be interesting.
peaks, would be interesting.
Motzkin numbers have been extended to what is called higher-rank, where Up steps and Level steps can be greater than one. There are statements that can reduce nesting level by more than one, e.g., breaking out of loops, but no constructs increase nesting by more than one (that I can think of). Perhaps the rather complicated relationship can be adapted to greater Down steps.
Other kinds of statements can increase nesting level, e.g., for-statements and while-statements. I have not yet spotted any papers dealing with the case where an Up step eventually has a corresponding Down step at the appropriate nesting level (needed to handle different kinds of nest-creating constructs). Pointers welcome. A related problem is handling if-statements containing else arms, here there is an associated increase in nesting.
What characteristics does human written code have that results in it having particular kinds of silhouettes? I have been thinking about this for a while, but have no good answers.
If you spot any Motzkin related papers that you think could be applied to source code analysis, please let me know.
Update
A solution to the Number of statement sequences possible using N if-statements problem.
Calculating statement execution likelihood
In the following code, how often will the variable b be incremented, compared to a?
If we assume that the variables x and y have values drawn from the same distribution, then the condition (x < y) will be true 50% of the time (ignoring the situation where both values are equal), i.e., b will be incremented half as often as a.
a++; if (x < y) { b++; if (x < z) { c++; } } |
If the value of z is drawn from the same distribution as x and y, how often will c be incremented compared to a?
The test (x < y) reduces the possible values that x can take, which means that in the comparison (x < z), the value of x is no longer drawn from the same distribution as z.
Since we are assuming that z and y are drawn from the same distribution, there is a 50% chance that (z < y).
If we assume that (z < y), then the values of x and z are drawn from the same distribution, and in this case there is a 50% change that (x < z) is true.
Combining these two cases, we deduce that, given the statement a++; is executed, there is a 25% probability that the statement c++; is executed.
If the condition (x < z) is replaced by (x > z), the expected probability remains unchanged.
If the values of x, y, and z are not drawn from the same distribution, things get complicated.
Let's assume that the probability of particular values of x and y occurring are 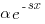 and
and 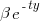 , respectively. The constants
, respectively. The constants 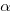 and
and 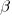 are needed to ensure that both probabilities sum to one; the exponents
are needed to ensure that both probabilities sum to one; the exponents 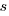 and
and  control the distribution of values. What is the probability that
control the distribution of values. What is the probability that (x < y) is true?
Probability theory tells us that 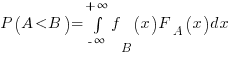 , where:
, where: 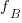 is the probability distribution function for
is the probability distribution function for 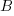 (in this case:
(in this case: 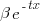 ), and
), and 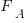 the cumulative probability distribution for
the cumulative probability distribution for 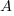 (in this case:
(in this case: 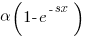 ).
).
Doing the maths gives the probability of (x < y) being true as: 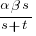 .
.
The (x < z) case can be similarly derived, and combining everything is just a matter of getting the algebra right; it is left as an exercise to the reader :-)
Recent Comments