Archive
Including natural language text topics in a regression model
The implementation records for a project sometimes include a brief description of each task implemented. There will be some degree of similarity between the implementation of some tasks. Is it possible to calculate the degree of similarity between tasks from the text in the task descriptions?
Over the years, various approaches to measuring document similarity have been proposed (more than you probably want to know about natural language processing).
One of the oldest, simplest and widely used technique is term frequency–inverse document frequency (tf-idf), which is based on counting word frequencies, i.e., is word context is ignored. This technique can work well when there are a sufficient number of words to ensure a good enough overlap between similar documents.
When the description consists of a sentence or two (i.e., a summary), the problem becomes one of sentence similarity, not document similarity (so tf-idf is unlikely to be of any use).
Word context, in a sentence, underpins the word embedding approach, which represents a word by an n-dimensional vector calculated from the local sentence context in which the word occurs (derived from a large amount of text). Words that are closer, in this vector space, are expected to have similar meanings. One technique for calculating the similarity between sentences is to compare the averages of the word embedding of the words they contain. However, care is needed; words appearing in the same context can create sentences having different meanings, as in the following (calculated sentence similarity in the comments):
import spacy nlp=spacy.load("en_core_web_md") # _md model needed for word vectors nlp("the screen is black").similarity(nlp("the screen is white")) # 0.9768339369182919 # closer to 1 the more similar the sentences nlp("implementing widgets would be little effort").similarity(nlp("implementing widgets would be a huge effort")) # 0.9636533803238744 nlp("the screen is black").similarity(nlp("implementing widgets would be a huge effort")) # 0.6596892830922606 |
The first pair of sentences are similar in that they are about the characteristics of an object (i.e., its colour), while the second pair are similar in that are about the quantity of something (i.e., implementation effort), and the third pair are not that similar.
The words in a document, or summary, are about some collection of topics. A set of related documents are likely to contain a discussion of a set of related topics in varying degrees. Latent Dirichlet allocation (LDA) is a widely used technique for calculating a set of (unseen) topics from a set of documents and their contained words.
A recent paper attempted to estimate task effort based on the similarity of the task descriptions (using tf-idf). My last semi-serious attempt to extract useful information from text, some years ago, was a miserable failure (it’s a very hard problem). Perhaps better techniques and tools are now available for me to leverage (my interest is in understanding what is going on, not making predictions).
My initial idea was to extract topics from task data, and then try to add these to regression models of task effort estimation, to see what impact they had. Searching to find out what researchers have recently been doing in this area, I was pleased to see that others were ahead of me, and had implemented R packages to do the heavy lifting, in particular:
- The
stmpackage supports the creation of Structural Topic Models; these add support for covariates to influence the process of fitting LDA models, i.e., a correlation between the topics and other variables in the data. Uses of STM appear to be oriented towards teasing out differences in topics associated with different values of some variable (e.g., political party), and the package authors have written papers analysing political data. - The
psychtmpackage supports what the authors call supervised latent Dirichlet allocation with covariates (SLDAX). This handles all the details needed to include the extracted LDA topics in a regression model; exactly what I was after. The user interface and documentation for this package is not as polished as thestmpackage, but the code held together as I fumbled my way through.
To experiment using these two packages I used the SiP dataset, which includes summary text for each task, and I have previously analysed the estimation task data.
The stm package:
The textProcessor function handles all the details of converting a vector of strings (e.g., summary text) to internal form (i.e., handling conversion to lower case, removing stop words, stemming, etc).
One of the input variables to the LDA process is the number of topics to use. Picking this value is something of a black art, and various functions are available for calculating and displaying concepts such as topic semantic coherence and exclusivity, the most commonly used words associated with a topic, and the documents in which these topics occur. Deciding the extent to which 10 or 15 topics produced the best results (values that sounded like a good idea to me) required domain knowledge that I did not have. The plot below shows the extent to which the words in topic 5 were associated with the Category column having the value “Development” or “Management” (code+data):
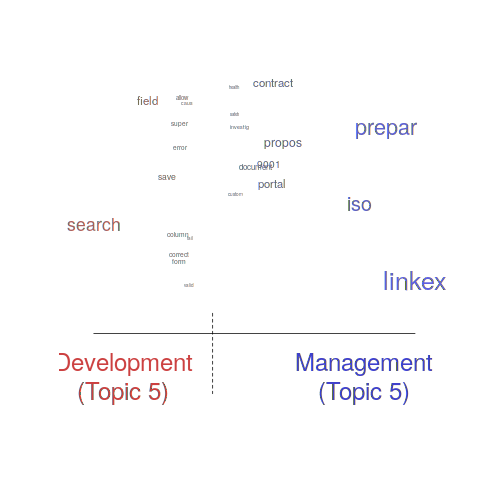
The psychtm package:
The prep_docs function is not as polished as the equivalent stm function, but the package’s first release was just last year.
After the data has been prepared, the call to fit a regression model that includes the LDA extracted topics is straightforward:
sip_topic_mod=gibbs_sldax(log(HoursActual) ~ log(HoursEstimate), data = cl_info,
docs = docs_vocab$documents, model = "sldax",
K = 10 # number of topics) |
where: log(HoursActual) ~ log(HoursEstimate) is the simplest model fitted in the original analysis.
The fitted model had the form: 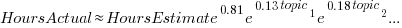 , with the calculated coefficient for some topics not being significant. The value
, with the calculated coefficient for some topics not being significant. The value 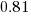 is close to that fitted in the original model. The value of
is close to that fitted in the original model. The value of 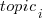 is the fraction of the
is the fraction of the 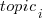 calculated to be present in the Summary text of the corresponding task.
calculated to be present in the Summary text of the corresponding task.
I’m please to see that a regression model can be improved by adding topics derived from the Summary text.
The SiP data includes other information such as work Category (e.g., development, management), ProjectCode and DeveloperId. It is to be expected that these factors will have some impact on the words appearing in a task Summary, and hence the topics (the stm analysis showed this effect for Category).
When the model formula is changed to: log(HoursActual) ~ log(HoursEstimate)+ProjectCode, the quality of fit for most topics became very poor. Is this because ProjectCode and topics conveyed very similar information, or did I need to be more sophisticated when extracting topic models? This needs further investigation.
Can topic models be used to build prediction models?
Summary text can only be used to make predictions if it is available before the event being predicted, e.g., available before a task is completed and the actual effort is known. My interest in model building is to understand the processes involved, so I am not worried about when the text was created.
My own habit is to update, or even create Summary text once a task is complete. I asked Stephen Cullen, my co-author on the original analysis and author of many of the Summary texts, about the process of creating the SiP Summary sentences. His reply was that the Summary field was an active document that was updated over time. I suspect the same is true for many task descriptions.
Not all estimation data includes as much information as the SiP dataset. If Summary text is one of the few pieces of information available, it may be possible to use it as a proxy for missing columns.
Perhaps it is possible to extract information from the SiP Summary text that is not also contained in the other recorded information. Having been successful this far, I will continue to investigate.
Another nail for the coffin of past effort estimation research
Programs are built from lines of code written by programmers. Lines of code played a starring role in many early effort estimation techniques (section 5.3.1 of my book). Why would anybody think that it was even possible to accurately estimate the number of lines of code needed to implement a library/program, let alone use it for estimating effort?
Until recently, say up to the early 1990s, there were lots of different computer systems, some with multiple (incompatible’ish) operating systems, almost non-existent selection of non-vendor supplied libraries/packages, and programs providing more-or-less the same functionality were written more-or-less from scratch by different people/teams. People knew people who had done it before, or even done it before themselves, so information on lines of code was available.
The numeric values for the parameters appearing in models were obtained by fitting data on recorded effort and lines needed to implement various programs (63 sets of values, one for each of the 63 programs in the case of COCOMO).
How accurate is estimated lines of code likely to be (this estimate will be plugged into a model fitted using actual lines of code)?
I’m not asking about the accuracy of effort estimates calculated using techniques based on lines of code; studies repeatedly show very poor accuracy.
There is data showing that different people implement the same functionality with programs containing a wide range of number of lines of code, e.g., the 3n+1 problem.
I recently discovered, tucked away in a dataset I had previously analyzed, developer estimates of the number of lines of code they expected to add/modify/delete to implement some functionality, along with the actuals.
The following plot shows estimated added+modified lines of code against actual, for 2,692 tasks. The fitted regression line, in red, is: 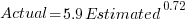 (the standard error on the exponent is
(the standard error on the exponent is 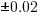 ), the green line shows
), the green line shows 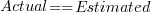 (code+data):
(code+data):
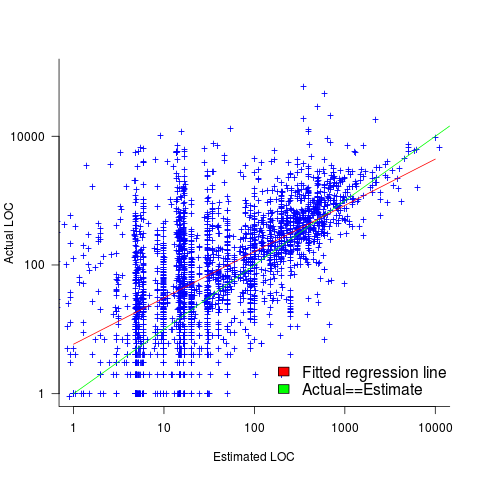
The fitted red line, for lines of code, shows the pattern commonly seen with effort estimation, i.e., underestimating small values and over estimating large values; but there is a much wider spread of actuals, and the cross-over point is much further up (if estimates below 50-lines are excluded, the exponent increases to 0.92, and the intercept decreases to 2, and the line shifts a bit.). The vertical river of actuals either side of the 10-LOC estimate looks very odd (estimating such small values happen when people estimate everything).
My article pointing out that software effort estimation is mostly fake research has been widely read (it appears in the first three results returned by a Google search on software fake research). The early researchers did some real research to build these models, but later researchers have been blindly following the early ‘prophets’ (i.e., later research is fake).
Lines of code probably does have an impact on effort, but estimating lines of code is a fool’s errand, and plugging estimates into models built from actuals is just crazy.
Software effort estimation is mostly fake research
Effort estimation is an important component of any project, software or otherwise. While effort estimation is something that everybody in industry is involved with on a regular basis, it is a niche topic in software engineering research. The problem is researcher attitude (e.g., they are unwilling to venture into the wilds of industry), which has stopped them acquiring the estimation data needed to build realistic models. A few intrepid people have risked an assault on their ego and talked to people in industry, the outcome has been, until very recently, a small collection of tiny estimation datasets.
In a research context, the term effort estimation is actually a hang over from the 1970s; effort correction more accurately describes the behavior of most models since the 1990s. In the 1970s, models took various quantities (e.g., estimated lines of code) and calculated an effort estimate. Later models have included an estimate as input to the model, producing a corrected estimate as output. For the sake of appearances, I will use existing terminology.
Which effort estimation datasets do researchers tend to use?
A 2012 review of datasets used for effort estimation using machine learning between 1991-2010, found that the top three were: Desharnias with 24 papers (29%), COCOMO with 19 papers (23%) and ISBSG with 17. A 2019 review of datasets used for effort estimation using machine learning between 1991 and 2017, found the top three to be NASA with 17 papers (23%), the COCOMO data and ISBSG were joint second with 16 papers (21%), and Desharnais was third with 14. The 2012 review included more sources in its search than the 2019 review, and subjectively your author has noticed a greater use of the NASA dataset over the last five years or so.
How large are these datasets that have attracted so many research papers?
The NASA dataset contains 93 rows (that is not a typo, there is no power-of-ten missing), COCOMO 63 rows, Desharnais 81 rows, and ISBSG is licensed by the International Software Benchmarking Standards Group (academics can apply for a limited time use for research purposes, i.e., not pay the $3,000 annual subscription). The China dataset contains 499 rows, and is sometimes used (there is no mention of a supercomputer being required for this amount of data ;-).
Why are researchers involved in software effort estimation feeding tiny datasets from the 1980s-1990s into machine learning algorithms?
Grant money. Research projects are more likely to be funded if they use a trendy technique, and for the last decade machine learning has been the trendiest technique in software engineering research. What data is available to learn from? Those estimation datasets that were flogged to death in the 1990s using non-machine learning techniques, e.g., regression.
Use of machine learning also has the advantage of not needing to know anything about the details of estimating software effort. Everything can be reduced to a discussion of the machine learning algorithms, with performance judged by a chosen error metric. Nobody actually looks at the predicted estimates to discover that the models are essentially producing the same answer, e.g., one learner predicts 43 months, 2 weeks, 4 days, 6 hours, 47 minutes and 11 seconds, while a ‘better’ fitting one predicts 43 months, 2 weeks, 2 days, 6 hours, 27 minutes and 51 seconds.
How many ways are there to do machine learning on datasets containing less than 100 rows?
A paper from 2012 evaluated the possibilities using 9-learners times 10 data-preprocessing options (e.g., log transform or discretization) times 7-error estimation metrics giving 630 possible final models; they picked the top 10 performers.
This 2012 study has not stopped researchers continuing to twiddle away on the option’s nobs available to them; anything to keep the paper mills running.
To quote the authors of one review paper: “Unfortunately, we found that very few papers (including most of our own) paid any attention at all to properties of the data set.”
Agile techniques are widely used these days, and datasets from the 1990s are not applicable. What datasets do researchers use to build Agile effort estimation models?
A 2020 review of Agile development effort estimation found 73 papers. The most popular data set, containing 21 rows, was used by nine papers. Three papers used simulated data! At least some authors were going out and finding data, even if it contains fewer rows than the NASA dataset.
As researchers in business schools have shown, large datasets can be obtained from industry; ISBSG actively solicits data from industry and now has data on 9,500+ projects (as far as I can tell a small amount for each project, but that is still a lot of projects).
Are there any estimates on GitHub? Some Open source projects use JIRA, which includes support for making estimates. Some story point estimates can be found on GitHub, but the actuals are missing.
A handful of researchers have obtained and released estimation datasets containing thousands of rows, e.g., the SiP dataset contains 10,100 rows and the CESAW dataset contains over 40,000 rows. These datasets are generally ignored, perhaps because when presented with lots of real data, researchers have no idea what to do with it.
Learning useful stuff from the Projects chapter of my book
What useful, practical things might professional software developers learn from the Projects chapter in my evidence-based software engineering book?
This week I checked the projects chapter; what useful things did I learn (combined with everything I learned during all the other weeks spent working on this chapter)?
There turned out to be around three to four times more data publicly available than I had first thought. This is good, but there is a trap for the unweary. For many topics there is one data set, and that one data set may not be representative. What is needed is a selection of data from various sources, all relating to a given topic.
Some data is better than no data, provided small data sets are treated with caution.
Estimation is a popular research topic: how long will a project take and how much will it cost.
After reading all the papers I learned that existing estimation models are even more unreliable than I had thought, and what is more, there are plenty of published benchmarks showing how unreliable the models really are (these papers never seem to get cited).
Models that include lines of code in the estimation process (i.e., the majority of models) need a good estimate of the likely number of lines in the final software system. One issue that nobody had considered was the impact of developer variability on the number of lines written to implement the same functionality, which turns out to be large. Oops.
Machine learning has infested effort estimation research. What the machine learning models actually do is estimate adjustment, i.e., they do not create their own estimate but adjust one passed in as input to the model. Most estimation data sets are tiny, and only contain a few different variables; unless the estimate is included in the training phase, the generated model produces laughable results. Oops.
The good news is that there appear to be lots of recurring patterns in the project data. This is good news because recurring patterns are something to be explained by a theory of software project development (apparent randomness is bad news, from the perspective of coming up with a model of what is going on). I think we are still a long way from having workable theories, but seeing patterns is a good sign that one or more theories will be possible.
I think that the main takeaway from this chapter is that software often has a short lifetime. People in industry probably have a vague feeling that this is true, from experience with short-lived projects. It is not cost effective to approach commercial software development from the perspective that the code will live a long time; some code does live a long time, but most dies young. I see the implications of this reality being a major source of contention with those in academia who have spent too long babbling away in front of teenagers (teaching the creation of idealized software that lives on forever), and little or no time building software systems.
A lot of software is written by teams of people, however, there is not a lot of data available on teams (software or otherwise). Given the difficulty of hiring developers, companies have to make do with what they have, so a theory of software teams might not be that useful in practice.
Readers might have a completely different learning experience from reading the projects chapter. What useful things did you learn from the projects chapter?
Effort estimation’s inaccurate past and the way forward
Almost since people started building software systems, effort estimation has been a hot topic for researchers.
Effort estimation models are necessarily driven by the available data (the Putnam model is one of few whose theory is based on more than arm waving). General information about source code can often be obtained (e.g., size in lines of code), and before package software and open source, software with roughly the same functionality was being implemented in lots of organizations.
Estimation models based on source code characteristics proliferated, e.g., COCOMO. What these models overlooked was human variability in implementing the same functionality (a standard deviation that is 25% of the actual size is going to introduce a lot of uncertainty into any effort estimate), along with the more obvious assumption that effort was closely tied to source code characteristics.
The advent of high-tech clueless button pushing machine learning created a resurgence of new effort estimation models; actually they are estimation adjustment models, because they require an initial estimate as one of the input variables. Creating a machine learned model requires a list of estimated/actual values, along with any other available information, to build a mapping function.
The sparseness of the data to learn from (at most a few hundred observations of half-a-dozen measured variables, and usually less) has not prevented a stream of puffed-up publications making all kinds of unfounded claims.
Until a few years ago the available public estimation data did not include any information about who made the estimate. Once estimation data contained the information needed to distinguish the different people making estimates, the uncertainty introduced by human variability was revealed (some consistently underestimating, others consistently overestimating, with 25% difference between two estimators being common, and a factor of two difference between some pairs of estimators).
How much accuracy is it realistic to expect with effort estimates?
At the moment we don’t have enough information on the software development process to be able to create a realistic model; without a realistic model of the development process, it’s a waste of time complaining about the availability of information to feed into a model.
I think a project simulation model is the only technique capable of creating a good enough model for use in industry; something like Abdel-Hamid’s tour de force PhD thesis (he also ignores my emails).
We are still in the early stages of finding out the components that need to be fitted together to build a model of software development, e.g., round numbers.
Even if all attempts to build such a model fail, there will be payback from a better understanding of the development process.
A prisoner’s dilemma when agreeing to a management schedule
Two software developers, both looking for promotion/pay-rise by gaining favorable management reviews, are regularly given projects to complete by a date specified by management; the project schedules are sometimes unachievable, with probability 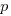 .
.
Let’s assume that both developers are simultaneously given a project, and the corresponding schedule. If the specified schedule is unachievable, High quality work can only be performed by asking for more time, otherwise performing Low quality work is the only way of meeting the schedule.
If either developer faces an unachievable deadline, they have to immediately decide whether to produce High or Low quality work. A High quality decision requires that they ask management for more time, and incur a penalty they perceive to be  (saying they cannot meet the specified schedule makes them feel less worthy of a promotion/pay-rise); a Low quality decision is perceived to be likely to incur a penalty of
(saying they cannot meet the specified schedule makes them feel less worthy of a promotion/pay-rise); a Low quality decision is perceived to be likely to incur a penalty of 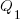 (because of its possible downstream impact on project completion), if one developer chooses Low, and
(because of its possible downstream impact on project completion), if one developer chooses Low, and 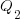 , if both developers choose Low. It is assumed that:
, if both developers choose Low. It is assumed that: 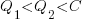 .
.
This is a prisoner’s dilemma problem. The following mathematical results are taken from: The Effects of Time Pressure on Quality in Software Development: An Agency Model, by Robert D. Austin (cannot find a downloadable pdf).
There are two Nash equilibriums, for the decision made by the two developers: Low-Low and High-High (i.e., both perform Low quality work, or both perform High quality work). Low-High is not a stable equilibrium, in that on the next iteration the two developers may switch their decisions.
High-High is a pure strategy (i.e., always use it), when: 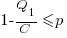
High-High is Pareto superior to Low-Low when: 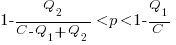
How might management use this analysis to increase the likelihood that a High-High quality decision is made?
Evidence shows that 50% of developer estimates, of task effort, underestimate the actual effort; there is sufficient uncertainty in software development that the likelihood of consistently produce accurate estimates is low (i.e., 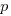 is a very fuzzy quantity). Managers wanting to increase the likelihood of a High-High decision could be generous when setting deadlines (e.g., multiple developer estimates by 200%, when setting the deadline for delivery), but managers are often under pressure from customers, to specify aggressively short deadlines.
is a very fuzzy quantity). Managers wanting to increase the likelihood of a High-High decision could be generous when setting deadlines (e.g., multiple developer estimates by 200%, when setting the deadline for delivery), but managers are often under pressure from customers, to specify aggressively short deadlines.
The penalty for a developer admitting that they cannot deliver by the specified schedule,  , could be set very low (e.g., by management not taking this factor into account when deciding developer promotion/pay-rise). But this might encourage developers to always give this response. If all developers mutually agreed to cooperate, to always give this response, none of them would lose relative to the others; but there is an incentive for the more capable developers to defect, and the less capable developers to want to use this strategy.
, could be set very low (e.g., by management not taking this factor into account when deciding developer promotion/pay-rise). But this might encourage developers to always give this response. If all developers mutually agreed to cooperate, to always give this response, none of them would lose relative to the others; but there is an incentive for the more capable developers to defect, and the less capable developers to want to use this strategy.
Regular code reviews are a possible technique for motivating High-High, by increasing the likelihood of any lone Low decision being detected. A Low-Low decision may go unreported by those involved.
To summarise: an interesting analysis that appears to have no practical use, because reasonable estimates of the values of the variables involved are unavailable.
Wanted: 99 effort estimation datasets
Every now and again, I stumble upon a really interesting dataset. Previously, when this happened I wrote an extensive blog post; but the SiP dataset was just too big and too detailed, it called out for a more expansive treatment.
How big is the SiP effort estimation dataset? It contains 10,100 unique task estimates, from ten years of commercial development using Agile. That’s around two orders of magnitude larger than other, current, public effort datasets.
How detailed is the SiP effort estimation dataset? It contains the (anonymized) identity of the 22 developers making the estimates, for one of 20 project codes, dates, plus various associated items. Other effort estimation datasets usually just contain values for estimated effort and actual effort.
Data analysis is a conversation between the person doing the analysis and the person(s) with knowledge of the application domain from which the data came. The aim is to discover information that is of practical use to the people working in the application domain.
I suggested to Stephen Cullum (the person I got talking to at a workshop, a director of Software in Partnership Ltd, and supplier of data) that we write a paper having the form of a conversation about the data; he bravely agreed.
The result is now available: A conversation around the analysis of the SiP effort estimation dataset.
What next?
I’m looking forward to seeing what other people do with the SiP dataset. There are surely other patterns waiting to be discovered, and what about building a simulation model based on the charcteristics of this data?
Turning software engineering into an evidence-based disciple requires a lot more data; I plan to go looking for more large datasets.
Software engineering researchers are a remarkable unambitious bunch of people. The SiP dataset should be viewed as the first of 100 such datasets. With 100 datasets we can start to draw general, believable conclusions about the processes involved in software effort estimation.
Readers, today is the day you start asking managers to make any software engineering data they have publicly available. Yes, it can be anonymized (I am willing to do that for people who are looking to release data). Yes, ‘old’ data is useful (data from the 1980s could have an interesting story to tell; SiP runs from 2004-2014). Yes, I will analyze any interesting data that is made public for free.
Ask, and you shall receive.
Impact of team size on planning, when sitting around a table
A recent blog post by Allan Kelly caught my attention; on Monday Allan sent me some comments on the draft of my book and I got to ask for a copy of his data (you don’t need your own software engineering data before sending me comments).
During an Agile training course he gives, Allan runs an exercise based on an extended version of the XP game. The basic points are: people form into teams, a task is announced, teams have to estimate how long it will take them to complete the task and then to plan the task implementation. Allan recorded information on team size, time spent estimating and time spent planning (no information on the tasks, which were straightforward, e.g., fold a paper airplane).
In a recent post I gave a brief analysis of team size on productivity. What does this XP game data have to say about the impact of team size on performance?
We don’t have task information, but we do have two timing measurements for each team. With a bit of suck-it-and-see analysis, I found that the following equation explained 50% of the variance (code+data):
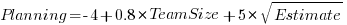
where: 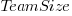 is the number of people on a team,
is the number of people on a team, 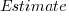 is the time in minutes the team spent estimating and
is the time in minutes the team spent estimating and 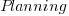 is time in minutes the team spent planning the task implementation.
is time in minutes the team spent planning the task implementation.
There was some flexibility in the numbers, depending on the method used to build the regression model.
The introduction of each new team member incurs a fixed overhead. Given that everybody is sitting together around a table, this is not surprising; or, perhaps the problem was so simply that nobody felt the need to give a personal response to everything said by everybody else; or, perhaps the exercise was run just before lunch and people were hungry.
I am not aware of any connection between time spent estimating and time spent planning, but then I know almost nothing about this kind of XP game exercise. That square-root looks interesting (an exponent of 0.4 or 0.6 was a slightly less good fit). Thoughts and experiences anybody?
Update: I forgot to mention that including the date of the workshop in the above model increases the variance explained to 90%. The date here is a proxy for the task being solved. A model that uses just the date explains 75% of the variance.
Recent Comments