Archive
Over/under estimation factor for ‘most estimates’
When asked to estimate the time taken to perform a software development related task, people regularly over or under estimate. What range of over/under estimation falls within the bounds of the term ‘most estimates’, i.e., the upper/lower bounds of the ratio 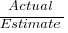 (an overestimate occurs when
(an overestimate occurs when 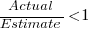 , an underestimate when
, an underestimate when 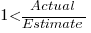 )?
)?
On Twitter, I have been citing a factor of two for over/under time estimates. This factor of two involves some assumptions and a personal interpretation.
The following analysis is based on the two major software task effort estimation datasets: SiP and CESAW. The tasks in both datasets are for internal projects (i.e., no tendering against competitors), and require at most a few hours work.
The following analysis is based on the SiP data.
Of the 8,252 unique tasks in the SiP data, 30% are underestimates, 37% exact, and 33% overestimates.
How do we go about calculating bounds for the over/under factor of most estimates (a previous post discussed calculating an accuracy metric over all estimates)?
A simplistic approach is to average over each of the overestimated and underestimated tasks. The plot below shows hours estimated against the ratio actual/estimated, for each task (code+data):
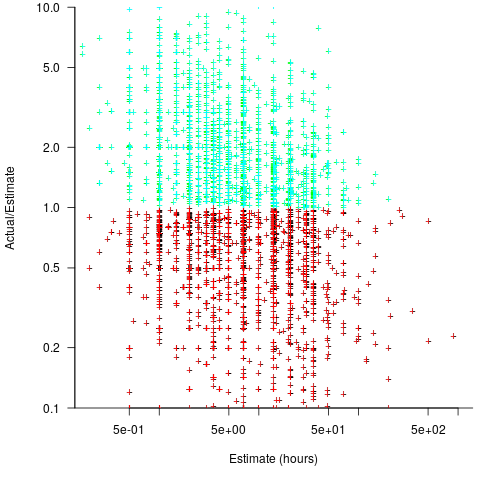
Averaging the over/under estimated tasks separately (using the geometric mean) gives 0.47 and 1.9 respectively, i.e., tasks are over/under estimated by a factor of two.
This approach fails to take into account the number of estimates that are over/under/equal, i.e., it ignores likelihood information.
A regression model takes into account the distribution of values, and we could adopt the fitted model’s prediction interval as the over/under confidence intervals. The prediction interval is the interval within which other observations are expected to fall, with some probability (R’s predict function uses one standard deviation).
The plot below shows a fitted regression model and prediction intervals at one standard deviation (68.3%) and two standard deviations (95%); the faint grey line shows Estimate == Actual (code+data):
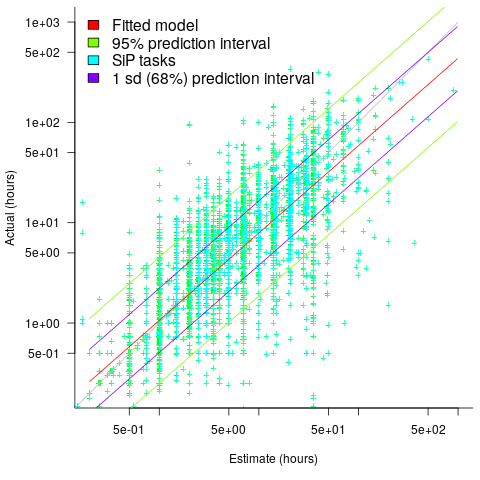
The fitted model tilts down from the upward direction of the Estimate == Actual line, consequently the over/under estimation factor depends on the size of the estimate. The table below lists the over/under estimation factor for low/high estimates at one & two standard deviations (68.3 and 95% probability).
People like simple answers (i.e., single values) and the mean value is a commonly used technique of summarising many values. The task estimate values are unevenly distributed and weighting the mean by the distribution of estimated values is more representative than, say, an evenly distributed set of estimates. The 5th and 6th columns in the table below list the weighted means at one/two standard deviations (the CESAW columns are the values for all projects in the CESAW data).
1 sd 2 sd Weighted mean CESAW
Low High Low High 1 sd 2 sd 1 sd 2 sd
Over 0.56 0.24 0.27 0.11 0.46 0.25 0.29 0.1
Under 2.4 1.0 4.9 2.0 2.00 4.1 2.4 6.5 |
The weighted means for over/under estimates are close to a factor of two of the actual (divide/multiply) within one standard deviation (68.3%), and a factor of four within two standard deviations (95%).
Why choose to give the one standard deviation factor, rather than the two? People talk of “most estimates”, but what percentage range does ‘most’ map to? I have tended to think of ‘most’ as more than two-thirds, e.g., at least one standard deviation (a recent study suggests that ‘most’ usage peaks at 80-85%), and I think of two standard deviations as ‘nearly all’ (i.e., 95%; there are probably people who call this ‘most’).
Perhaps a between two and four is a more appropriate answer (particularly since the bounds are wider for the CESAW data). Suggestions welcome.
Ada updated to support undefined behavior
The Ada language has now almost completely disappeared from developer consciousness and the Ada Standards’ committee has decided this desperate situation calls for desperate actions.
Undefined behavior in programming languages has been getting a lot of publicity over the last few years. It might not be good publicity, but the Ada committee has taken to heart the old adage ‘The only thing worse than being talked about is not being talked about.’
While the Ada standard does not use the phrase undefined behavior, it does contain a very close equivalent. The Ada community has bitten the bullet and decreed that constructs previously denoted by the term bounded error shall henceforth be referred to as undefined behavior. Technically, constructs generating a bounded error have effectively always been undefined behavior, but the original positioning of Ada as a sophisticated language suitable for critical applications required something less in-your-face unsafe sounding.
Will this minor change of wording (ISO rules are very strict on what changes can be made to published standards without going through long winded voting procedures) make any difference? I guess it will enable Ada users to jump on the ‘undefined behavior’ bandwagon (their claims that Ada was better because it did not contain undefined behavior always has the effect of annoying people, rather than generating any interest in changing languages).
I think there is a bigger public perception problem than the terminology used to denote undefined behavior. Ada Lovelace was born 200 years ago and gets lots of publicity as the first programmer; somehow this association with Lovelace has transferred to the language named after her, generating a perception of an old, fuddy-duddy language (being strongly typed has not helped, but this feature does appear to be coming back into fashion).
The following are some numbers from a while ago (both standards have been revised since these measurements were made).
In the Ada 2005 Standard there are:
36 occurrences of bounded error. 53 occurrences of the subsection header Erroneous execution and 116 occurrences of erroneous. 343 occurrences of implementation-defined. 373 occurrences of may, some of which describe optional behavior. 22 occurrences of must some of which that read as-if shall was intended. 38 occurrences of optional. zero occurrences of processor dependent and processor-dependent. 1,018 occurrences of shall of which 131 have the form shall not. 452 occurrences of should. 8 occurrences of undefined, one referencing to an undefined range, three having the form undefined range and the rest occurring in annexes (also see bounded error). • 89 occurrences of unspecified.
In the C99 Standard there are:
zero occurrences of bounded error. 3 occurrences of erroneous. 163 occurrences of implementation-defined. 862 occurrences of may. 1 occurrence of must. 34 occurrences of optional. zero occurrences of processor dependent and processor-dependent. 596 occurrences of shall of which 71 have the form shall not. 63 occurrences of should. 183 occurrences of undefined. 98 occurrences of unspecified.
In the C++ 2003 Standard (which now contains many more pages) there are:
zero occurrences of bounded error. 5 occurrences of erroneous. 236 occurrences of implementation-defined. 371 occurrences of may. 111 occurrences of must. 30 occurrences of optional. zero occurrences of processor dependent and processor-dependent. 779 occurrences of shall of which 211 have the form shall not. 38 occurrences of should. 195 occurrences of undefined. 113 occurrences of unspecified.
Tool for tuning the use of floating-point types
A common problem when writing code that performs floating-point arithmetic is figuring out which of the available three (usually) possible floating-point types to use (e.g., float, double or long double). Some language ‘solve’ this problem by only having one possibility (e.g., R) and some implementations of languages that offer three types use the same representation for all of them (e.g., 32 bits).
The type float often represents the least precision/range of values but occupies the smallest amount of storage and operations on it have traditionally been the fastest, type long double often represents the greatest precision/range of values but occupies the most storage and operations on it are generally the slowest. Applying the Goldilocks principle the type double is very often selected.
Anyone who has worked with floating-point values will be familiar with some of the ways they can bite very hard. Once a function that uses floating-point types is written the general advice is to leave it alone.
Precimonious is an interesting new tool that searches for possible performance/accuracy trade-offs; it randomly selects a floating-point declaration, changes the type used, executes the resulting program and compares the output against that produced by the original program. Users of the tool specify the maximum error (difference in output values) they are willing to accept and Precimonious searches for a combination of changes to the floating-point types contained within a program that result in a faster program that does not exceed this maximum error.
The performance improvements cited in the paper (which includes the doyen of floating-point in its long list of authors) cluster around zero and worthwhile double figure percentage (max 41.7%); sometimes no improvements were found until the maximum error was reduced from 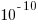 to
to 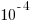 .
.
Perhaps a combination of Precimonious and a tool that attempts to improve accuracy is the next step 🙂
There is resistance to using search based methods to fix faults. Perhaps tools like Precimonious will help developers get used to the idea of search assisted software development.
I wonder how long it will be before we see commentary in bug reports such as the following:
- that combination of values was not in the Precimonious test set,
- Precimonious cannot find a sufficiently optimized program within the desired error tolerance for that rarely seen combination of values. Won’t fix.
Undefined behavior is a design decision
Every few years or so some group of people in the C/C++ community start writing about the constructs specified as having undefined behavior in those languages. A topic that always seems to be skipped is why a language committee would choose to specify that the behavior in a particular case was undefined.
A quick refresher for readers on the definition of Undefined behavior, from the C Standard: “behavior, upon use of a nonportable or erroneous program construct or of erroneous data, for which this International Standard imposes no requirements”. The two key features are that the behavior applies when an error has occurred and any behavior whatsoever is permitted after one of these errors occurs. Examples of constructs that have undefined behavior are divide by zero, the result of an arithmetic operation on a signed value not being representable in its type (i.e., overflowing) and indexing an array outside of its defined bounds.
The point to note about all undefined behaviors is that the C/C++ language committee could have chosen to specify the behavior that a conforming implementation is required to support. Some language specifications do attempt to explicitly define the behavior for all constructs, e.g., Java, while other languages have a smaller set of undefined behaviors (e.g., Ada, which uses the term Bounded error instead of undefined behavior; there are 35 of them in Ada 2005). To understand why languages take these different approaches we need to look at the language design aims.
The design aims of C included it being implementable for any processor and for the generated code to be efficient (I’m not sure to what extent these might still be major design aims for C++). Computing systems come in all shapes and sizes, some with hundreds of bytes of memory and others with gigabytes, some raise exceptions when certain operations occur while others set processor status flags and others don’t do anything special.
A willingness to accept whatever behavior happens to occur, in an error situation, is the price that has to be paid for efficient execution on a wide range of disparate processors. The C/C++ designers were willing to pay this price while while the Java designers were not, with the Ada designers willing to tolerate less variability than C/C++.
Undefined behavior need not be nasty behavior, an implementation could chose to generate a helpful message or try to recover from it.
There are C tools and compilers (when certain options are specified) that check, at runtime, for various kinds of undefined behavior. I am in the minority in having Boundschecker installed as my default C compiler (as the name suggests it checks that array and pointer accesses to an object are within the defined bounds); for reasons I don’t understand few C/C++ developers are willing to use tools like this. For production code I use a non-boundschecking compiler; I don’t know whether Ada programs are tested with the mandated bounds checking switched on and then have it switched off for the production version (this is what Pascal developers do, in my experience). Of course Java developers have no choice but to permanently live with checking turned on.
The number of companies that make a living selling runtime checking tools is a small percentage of the number of companies based on selling static analysis tools. There continues to be a steady stream of runtime checking tools appearing and quickly disappearing, but until a developers start being sent to jail for faults in their code I don’t foresee the market growing.
Optimizations to figure out when code need not be generated to perform a bounds check because the access is known to be within bounds is an active research area. These days the performance penalty is not so much executing the checking instructions but the disruption to the instruction pipeline caused by the branches that might be taken (if the bounds check fails).
The cost of all the checking required by Java is that the minimal permitted configuration requires at least 256K of memory (Oracle’s K virtual machine, used by the Java Micro Edition which is intended for embedded systems, also makes floating-point optional and allows implementations some freedom in how some constructs are handled). So the Java motto really out to be “Write once, run anywhere with at least 256K and don’t depend on floating-point”.
I have heard stories of Ada code being liberally scattered with various forms of unchecked (how the developer tells the compiler not to do any runtime checking) but have not seen any empirical analysis (a study of goto usage in Ada did not have any trouble finding plenty of uses to analyze).
Recent Comments