SEC wants prospectus source code to be published
The US Securities and Exchange Commission are proposing new rules involving the prospectuses for public offerings of asset-backed securities including publishing the source code used to calculate the contractual cash flow provisions.
Requiring that the source code used to perform the financial modeling for a prospectus be made available is an excellent idea. A prospectus document contains a huge number of technical details and more importantly for anybody trying to understand the thinking behind it, a lots of assumption. Writing a program requires that all necessary details be enumerated and appropriately connected together and more importantly creating code that can be meaningfully executed usually means making explicit any assumptions that were previously implicit.
There are parallels here with having access to the source code and data used to make climate predictions.
The authors of the proposals are naive to think that simply requiring source to be written in a language for which there is an open source implementation (i.e., Python) is all they need to specify for others to duplicate the program output generated by the proposer (I have submitted some suggestions to the SEC about the issues that need to be addressed). The suggestions that a formally defined language be used is equally naive.
The availability of this source code opens up some interesting commercial prospects. No, not selling analysis tools to financial institutions but selling them program fault information, e.g., under circumstance X the program incorrectly predicts A will happen when in fact B will actually happen. Of course companies know this will happen and will put a lot more effort into ensuring that their models/code is correct.
Will these disclosure rules change the characteristics of financial software? One characteristic that I’m sure will change is the percentage of swear words in the comments and identifiers.
Brief history of syntax error recovery
Good recovery from syntax errors encountered during compilation is hard to achieve. The two most common strategies are to insert one or more tokens or to delete one or more tokens. Make the wrong decision and a second syntax error will occur, often leading to another and soon the developer is flooded by a nonsensical list of error messages. Compiler writers soon learn that their first priority is ensuring that syntax error recovery does not result in lots of cascading errors. In languages that use a delimiter to indicate end of statement/declaration, usually a semicolon, the error recovery strategy of deleting all tokens until this delimiter is next encountered is remarkably effective.
The era of very good syntax error recovery was the 1970s and early 1980s. Developers working on mainframes might only be able to achieve one or two compilations per day on a batch oriented mainframe and they were not happy if a misplaced comma or space resulted in a whole day being wasted. Most compilers were rented for lots of money and customer demand resulted in some very fancy error recovery strategies.
Borland’s Turbo Pascal had a very different approach to handling errors in code, it stopped processing the source as soon as one was detected. The combination of amazing compilation rates and an interactive environment (MS-DOS running on the machine in front of the developer) made this approach hugely attractive.
To a large extent syntax error recovery has been driven by the methods commonly used to write parsers. Many compilers use a table driven approach to syntax analysis with the tables being generated by parser generator tools such as Yacc. During the 1970s and 80s a lot of the research on parser generators was aimed at reducing the size of the generated tables. A table of 10k bytes was a significant percentage of available storage for machines that supported a maximum of 64k of memory. Some parser table compression techniques involve assuming the default behavior and then handling any special cases when these defaults are found not to apply, but one consequence is that context information needed for good error recovery is often not available when an error is detected. The last major release of Yacc from AT&T in the early 1990s managed another reduction in table size, just as typical storage sizes were getting into the ten of megabytes, but at the expense of increasing the difficulty of doing good error recovery.
While there are still some application areas where the amount of storage occupied by parser tables is still a big issue, e.g., the embedded market, developers of parser generators such as Bison ought to start addressing the needs of users wanting to do good error recovery and who are willing to accept larger tables.
I am pleased to see that the LLVM project is making an effort to provide good syntax error recovery. A frustrating barrier to providing better error recovery is lack of information on the kinds of syntax errors commonly made by developers; there are a few papers and reports containing small scale measurements of errors made by students. Perhaps the LLVM developers will provide a mechanism for automatically collecting compilation errors and providing users with the option to send the results to the LLVM project.
One of my favorite syntax error recovery techniques (implemented in a PL/1 mainframe compiler; I have never been able to justify implementing it on any project I worked on) is the following:
// Use of an undeclared identifier is a syntax error in C and some other // languages, while in other languages it is a semantic error. // no identifier with name result visible here { int result; ... result=... ... } ... calc=result*2; // Error reported by most compilers is use of an undeclared variable |
The ‘real’ error is probably the misplaced closing bracket. Other possibilities include result being a misspelled version of another variable or the assignment to calc being in the wrong place.
There seems to be a trend over the last 20 years to create languages that require more and more semantic information during parsing. Deciphering a syntax error today can involve a lot more than figuring out which surrounding tokens have been omitted or misplaced, information on which types are in scope and visible (oh for the days when that meant the same thing) and where they might be found in the umpteen thousand lines of included source has to be distilled and presented to the developer in a helpful message.
For a long time compilers have primarily been benchmarked on the quality of their code. With every diminishing returns from improved optimization, the increasing complexity of languages and the increasing volume of header code pulled in during compilation perhaps the quality of syntax error recovery will grow in importance.
Number of digits in floating-point literals
Some of the interesting floating-point literals detected by the numbers program not only look uninteresting but plain wrong. For instance, almost every program I analyze appears to contain a literal denoting the ratio of the diameter of the Earth to at least one minor planet. One problem is that most of the numbers contained in the interesting number database are only likely to occur in very specific circumstances and as the size of this database grows the percentage of inappropriate matches grows.
I could (and at some point probably will have to) assign an interestingness level to numbers, but this goes against one of the original aims of identifying the operations performed by unknown source.
An alternative idea is to create a connection between the fuzziness of the matching process and the probability of the literal being encountered in code. For instance, a more exact match might be required for 0.5 because it contains few mantissa digits and sits within a range of values that are commonly encountered, while a much fuzzier match might be used for 1.879623e+3 because it contains more digits and occupies a less commonly encountered range of values.
Floating-point literals often contain leading or trailing zeros, e.g., 0.001, 100.0, 1e+2
or 0.50. Does the presence of these zeros change the probability of a particular mantissa being encountered? For instance the literals 100.0 and 1e+2 have the same numeric value but different numbers of mantissa digits.
Another issue is developer intent. Why did a developer write 0.50, did they simply want two digits to appear after the decimal point because the surrounding literals in the source contain two digits and it makes the visual appearance look better or does this usage denote a quantity whose accuracy is known to two decimal digits?
The following figure is derived from 1 million non-zero floating-point literals contained in ten large, computationally intensive programs.
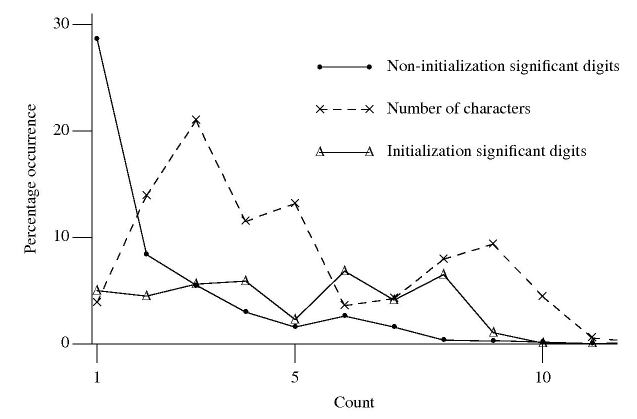
The dashed line denotes the percentage of mantissas containing a given number of characters, including leading/trailing zeros and any decimal point.
The two solid lines denote the digit count of the mantissas with any leading/trailing zeros removed, along with any decimal point, e.g., both 100.0 and 1e+2 would be considered to contain one digit.
It seemed to me that floating-point literals appearing within an initializer attached to a variable definition often contain more digits than literals that appear elsewhere. The solid, triangle tagged, solid line that spends most of its time around 5% are floating-point literals appearing within an initializer (to be exact they are literals separated from another literal by a comma {with some simplistic handling of Fortran line continuation}). The bullet tagged line are all other literals.
I was partially right about the characteristics of floating-point literals in initializers. It turns out the probability of encountering a mantissa containing a given number of digits is approximately constant within an initializer (a more sophisticated analysis might show an upward trend with increasing numbers of digits).
The mantissa digit count outside of initializers has the kind of probability distribution I was looking for. Hopefully this distribution will contribute to a useful measure of interestingness.
What language was an executable originally written in?
Apple have recently added an unusual requirement to the iPhone developer agreement “Applications must be originally written in Objective-C, C, C++, or JavaScript …”. As has been pointed out elsewhere the real purpose is stop third party’s from acquiring any control over application development on Apple’s products; the banning of other languages is presumably regarded as acceptable collateral damage.
Is it possible to tell by analyzing an executable what language it was originally written in?
There are two ways in which executables contain source language ‘signatures’. Detecting these signatures requires knowledge of specific compiler behavior, i.e., a database of information about the behavior of compilers capable of creating the executables is needed.
Runtime library. Most compilers make use of a language specific runtime library, rather than generating inline code for some kinds of functionality. For instance, setjmp/longjmp in C and vtables in C++.
The presence of a known C runtime library does not guarantee that the application was originally written in C; it could have been written in Java and converted to C source.
The absence of a known C runtime library could mean that the source was compiled by a C compiler using a runtime system unknown to the analyzer.
The presence of a known Java, for instance, runtime library would suggest that the original source contained some Java. This kind of analysis would obviously require that the runtime library database not restrict itself to the ‘C’ languages.
Compiler behavior patterns. There is usually more than one way in which a source language construct can be translated to machine code and a compiler has to pick one of them. The perfect optimizing compiler would always make the optimal choice, but real compilers follow a fixed pattern of code generation for at least some language constructs (e.g., initialization of registers on function entry).
The presence of known code patterns in an executable is evidence that a particular compiler has been used; how much depends on the likelihood it could have been generated by other means and how many other patterns suggest the same compiler. In the case of the GNU Compiler Collection the source language might also be Fortran, Java or Ada; I don’t know enough about the behavior of GCC to provide an informed estimate of whether it is possible to recognize the source language from the translated form of constructs shared by several languages, I suspect not.
The fact that an executable can be decompiled to C is not a guarantee that it was originally written in C.
Some languages support source language constructs whose corresponding machine code is unlikely to ever be generated by source from another language. The Fortran computed goto allows constructs to be written that have no equivalent in the other languages supported by GCC (none of them allow statement labels appearing in a multi-way jump to appear before the jump test):
10 I=I+1 20 J=J+1 goto (10, 20, 30, 40) J 30 I=I+3 40 I=I*2 |
The presence of a compiled form of this kind of construct in the executable would be very suggestive of Fortran source.
Apple are famously paranoid and control freakery. It will be very interesting to see what level of compliance checking they decide to perform on executables submitted to the App Store.
On another note: What does “originally written” mean? For instance, many of the mathematical functions (e.g., sine, log, gamma, etc) contained in R were originally written in Fortran and translated to C for use in R; this C source is what is now maintained. Does this historical implementation decision mean that R cannot be legally ported to the iPhone?
Program analysis via information leakage
The use of software in high value transactions has created an interesting new field of software research that investigates the leakage of information from programs. The kind of information leaked, so-called sideband information, can take various forms, including:
- The amount of time taken to perform some operation. Many developers instinctively do their best to ensure that code does not take any longer to execute than it has to. In the case of one commonly used authentication system, the time taken to fail to authenticate an encryption key provided useful information on how close one trial encryption-key was compared to another (the closer the trial key to the actual key, the longer the authentication took to fail). The obvious implementation technique to foil this kind of attack is to add random delays into the authentication process.
It has even proved possible to perform timing attacks against a remote machine over the Internet to remote
- Use of some part of the value of secure information, by a system library function, to create the value passed back to the caller, e.g.,
if (secret_value & 0xf000) // Tell the caller that the top 'secret' four bits are set return 1; else return 0;
Researchers have been able to analyse the information flow of input values through some very large C programs.
- Analyse of network traffic routing information to work out who is talking to who. Various kinds of anonymizers have been created in attempt to make various forms of Internet traffic untraceable.
Any Internet program is accessible to information flow analysis. Using these techniques to analyse the search algorithm used by Google might be overly ambitious. A Google algorithm that might be within reach of is the one used by Adwords; the behavior of this algorithm is of interest to a growing number of people.
Information leakage techniques are becoming more widely known and developers working on programs containing a security component now need to consider how they can prevent information being leaked to attackers who sample program behavior looking for exploitable weaknesses.
Variations in the literal representation of Pi
The numbers system I am developing attempts to match numeric literals contained in a file against a database of interesting numbers. One of the things I did to quickly build a reasonably sized database of reliable values was to extract numeric literals from a few well known programs that I thought I could trust.
R is a widely used statistical package, and Maxima is a computer algebra system with a long history. Both contain a great deal of functionality and are actively maintained.
To my surprise, the source code of both packages contain a large variety of different literal values for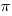 
, or to be exact, the number of digits contained in the literals varied by more than I expected. In the following table, the value to the left of the 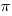representation is the number of occurrences; values listed in increasing literal order:
Maxima R
2 3.14159
14 3.141592
1 3.1415926
1 3.14159265 2 3.14159265
3 3.1415926535
4 3.14159265358979
14 3.141592653589793
3 3.1415926535897932385 3 3.1415926535897932385
9 3.14159265358979324
1 3.14159265359
1 3.1415927
1 3.141593
The comments in the Maxima source led me to believe that some thought had gone into ensuring that the numerical routines were robust. Over 3/4 of the literal representations of 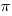have a precision comparable to at least that of 64-bit floating-point (I’m assuming an IEEE 754 representation in this post).
In the R source, approximately 2/3 of the literal representations of 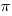have a precision comparable to that of 32-bit floating-point.
Closer examination of the source suggests one reason for this difference. Both packages make heavy use of existing code (translated from Fortran to Lisp for Maxima and from Fortran to C for R); using existing code makes good sense and because of its use in scientific and engineering applications many numerical libraries have been written in Fortran. Maxima has adapted the slatec library, whereas the R developers have used a variety of different libraries (e.g., specfun).
How important is variation in the representation of Pi?
- A calculation based on a literal that is only accurate to 32-bits is likely to be limited to that level of accuracy (unless errors cancel out somewhere).
- Inconsistencies in the value used to represent Pi are a source of error. These inconsistencies may be implicit, for instance literals used to denote a value derived from 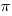such as
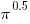often seem to be based on more precise values of Pi than appear in the code.
The obvious solution to this representation issue of creating a file containing definitions of all the frequently used literal values has possible drawbacks. For instance, numerical accuracy is a strange beast, and increasing the precision of one literal without doing the same for other literals appearing in a calculation can sometimes reduce the accuracy of the final result.
Pulling together existing libraries to build a package is often very cost-effective, but numerical accuracy is a slippery beast, and this inconsistent usage of literals suggests that developers from these two communities have not addressed the system level consequences of software reuse.
Update 6 April: After further rummaging around in the R source distribution, I found that things are not as bad as they first appear. Only two of the single precision instances of 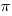listed above occur in the C or Fortran source code, the rest appear in support files (e.g., m4 scripts and R examples).
Using numeric literals to identify application domains
I regularly get to look at large quantities of source and need to quickly get some idea of the application domains used within the code; for instance, statistical calculations, atomic physics or astronomical calculations. What tool might I use to quickly provide a list of the application domains used within some large code base?
Within many domains some set of numbers are regularly encountered and for several years I have had the idea of extracting numeric literals from source and comparing them against a database of interesting numbers (broken down by application). I have finally gotten around to writing a program do this extraction and matching, its imaginatively called numbers. The hard part is creating an extensive database of interesting numbers and I’m hoping that that releasing everything under an open source license will encourage people to add their own lists of domain specific interesting numbers.
The initial release is limited to numeric literals containing a decimal point or exponent, i.e., floating-point literals. These tend to be much more domain specific than integer literals and should cut down on the noise, making it easier for me tune the matching algorithms without (currently numeric equality within some fuzz-factor and fuzzy-matching of digits in the mantissa).
Sometimes an algorithm uses a set of numbers (e.g., crc checking) and a match should only occur if all values from this set are encountered.
The larger the interesting number database the larger the probability of matching against a value from an unrelated domain. The list of atomic weights seem to be very susceptible to this problem. I am currently investigating whether the words that co-occur with an instance of a numeric literal can be used to reduce this problem, perhaps by requiring that at least one word from a provided list occur in the source before a match is flagged for some literal.
Some numbers frequently occur in several domains. I am hoping that the word analysis might also be used to help reduce the number of domains that need to be considered (ideally to one).
Another problem is how to handle conversion factors, that is the numeric constant used to convert one unit to another, e.g., meters to furlongs. What is needed is to calculate all unit conversion values from a small set of ‘basic’ units. It would probably be very interesting to find conversions between some rarely seen units occurring in source.
I have been a bit surprised by how many apparently non-interesting floating-point literals occur in source and am hoping that a larger database will turn them into interesting numbers (I suspect this will only occur for a small fraction of these literals).
Designing a processor for increased source portability costs
How might a vendor make it difficult for developers to port open source applications to their proprietary cpu? Keeping the instruction set secret is one technique, another is to design a cpu that breaks often relied upon assumptions that developers have about the characteristics of the architecture on which their code executes.
Of course breaking architectural assumptions does not prevent open source being ported to a platform, but could significantly slow down the migration; giving more time for customers to become locked into the software shipped with the product.
Which assumptions should be broken to have the maximum impact on porting open source? The major open source applications (e.g., Firefox, MySQL, etc) run on 32/64-bit architectures that have an unsigned address space, whose integer representation uses two’s complement arithmetic and arithmetic operations on these integer values wrap on over/underflow.
32/64-bit. There is plenty of experience showing that migrating code from 16-bit to 32-bit environments can involve a lot of effort (e.g., migrating Windows 286/386 code to the Intel 486) and plenty of companies are finding the migration from 32 to 64-bits costly.
Designing a 128-bit processor might not be cost effective, but what about a 40-bit processor, like a number of high end DSP chips? I suspect that there are many power-of-2 assumptions lurking in a lot of code. A 40-bit integer type could prove very expensive for ports of code written with a 32/64-bit mindset (dare I suggest a 20-bit short; DSP vendors have preferred 16-bits because it uses less storage?).
Unsigned address space (i.e., lowest address is zero). Some code assumes that addresses with the top bit set are at the top end of memory and not just below the middle (e.g., some garbage collectors). Processors having a signed address space (i.e., zero is in the middle of storage) are sufficiently rare (e.g., the Inmos Transputer) that source is unlikely to support a HAS_SIGNED_ADDRESS build option.
How much code might need to be rewritten? I have no idea. While the code is likely to be very important there might not be a lot of it.
Two’s complement. Developers are constantly told not to write code that relies on the internal representation of data types. However, they might be forgiven for thinking that nobody uses anything other than two’s complement to represent integer types these days (I suspect Univac does not have that much new code ported to it’s range of one’s complement machines).
How much code will break when ported to a one’s complement processor? The representation of negative numbers in one’s complement and two’s complement is different and the representation of positive numbers the same. In common usage positive values are significantly more common than negative values and many variables (having a signed type) never get to hold a negative value.
While I have no practical experience, or know of anybody who has, I suspect the use of one’s complement might not be that big a problem. If you have experience please comment.
Arithmetic that wraps (i.e., positive values overflow negative and negative values underflow positive). While expressions explicitly written to wrap might be rare, how many calculations contain intermediate values that have wrapped but deliver a correct final result because they are ‘unwrapped’ by a subsequent operation?
Arithmetic operation that saturate are needed in applications such as graphics where, for instance, increasing the brightness should not suddenly cause the darkest setting to occur. Some graphics processors include support for arithmetic operations that saturate.
The impact of saturation arithmetic on portability is difficult to judge. A lot of code contains variables having signed char and short types, but when they appear as the operand in a binary operation these are promoted to int in C/C++/etc which probably has sufficient range not to overflow (most values created during program execution are small). Again I am lacking in practical experience and comments are welcome.
Floating-point. Many programs do not make use of floating-point arithmetic and those that do rarely manipulate such values at the bit level. Using a non-IEEE 754 floating-point representation will probably have little impact on the portability of applications of interest to most users.
Update. Thanks to Cate for pointing out that I had forgotten to discuss why using non-8-bit chars does is not a worthwhile design decision.
Both POSIX and the C/C++ Standards require that the char type be represented in at least 8 bits. Computers supporting less than 8-bits were still being used in the early 80s (e.g., the much beloved ICL 1900 supported 6-bit characters). The C Standard also requires that char be the smallest unit of addressable storage, which means that it must be possible for a pointer to point at an object having a char type.
Designing a processor where the smallest unit of storage is greater than 8-bits but not a power-of-2 is likely to substantially increase all sorts of costs and complicate things enormously (e.g., interfaces to main memory which are designed to work with power of two interfaces). The purpose of this design is to increase other people’s cost, not the proprietary vendor’s cost.
What about that pointer requirement? Perhaps the smallest unit of storage that a pointer could address might be 16 or 40 bits? Such processors exist and compiler writers have used both solutions to the problems they present. One solution is for a pointer to contain the address of the storage location + offset of the byte within that storage (Cray used this approach on a processor whose pointers could only point at 64-bit chunks of storage, with the compiler generating the code to extract the appropriate byte), the other is to declare that the char type occupies 40-bits (several DSP compilers have taken this approach).
Having the compiler declare that char is not 8-bits wide would cause all sorts of grief, so lets not go there. What about the Cray compiler approach?
Some of the address bits on 64-bit processors are not used yet (because few customers need that amount of storage) so compiler writers could get around host-processor pointers not supporting the granularity needed to point at 8-bit objects by storing the extra information in ‘unused’ pointer bits (the compiler generating the appropriate insertion and extraction code). The end result is that the compiler can hide pointer addressability issues :-).
Minimum information needed for writing a code generator
If a compiler writer is faced with writing a back-end for an undocumented processor, what is the minimum amount of information that needs to be reverse engineered?
It is possible to implement a universal computer using a cpu that has a single instruction, subtract-and-branch-if-lessthan-or-equal-to-zero. This is all very well, but processors based on using a single instruction are a bit thin on the ground and the processor to hand is likely to support a larger number of simpler instructions.
A subtract-and-branch-if-lessthan-or-equal-to-zero instruction could be implemented on a register based machine using the appropriate sequence of load-from-memory, subtract-two-registers, store-register-to-memory and jump-if-subtract-lessthan-or-equal instructions. Information about other instructions, such as add and multiply, would be useful for code optimization. (The Turing machine model of computation is sufficiently far removed from how most programs and computers operate that it is not considered further.)
Are we done? In theory yes, in practice no. A couple pf practical problems have been glossed over; how do source literals (e.g., "Hello World") initially get written to storage, where does the storage used by the program come from and what is the file format of an executable?
Literals that are not created using an instruction (most processors have instructions for loading an integer constant into a register) are written to a part of the executable file that is read into storage by the loader on program startup. All well and good if we know enough about the format of an executable file to be able to correct generate this information and can get the operating system to put in the desired storage location. Otherwise we have to figure out some other solution.
If we know two storage locations containing values that differ by one a sequence of instructions could subtract one value from the other to eventually obtain any desired value. This bootstrap process would speed up as a wider range of know value/location pairs was built up.
How do we go about obtaining a chunk of storage? An executable file usually contains information on the initial amount of storage needed by a program when it is loaded. Calls to the heap manager are another way of obtaining storage. Again we need to know where to write the appropriate information in the executable file.
What minimum amount of storage might be expected to be available? A program executing within a stack/heap based memory model has a default amount of storage allocated for the stack (a minimum of 16k I believe under Mac OS X or iPhone OS). A program could treat the stack as its storage. Ideally what we need is the ability to access storage via an offset from the stack pointer, at worse we would have to adjust the stack pointer to the appropriate offset, pop the value into a register and then reset the stack pointer; storing would involve a push.
Having performed some calculation we probably want to communicate one or more values to the outside world. A call to a library routine, such as printf, needs information on the parameter passing conventions (e.g., which parameters get stored in which registers or have storage allocated for them {a function returning a structure type usually has the necessary storage allocated by the calling function with the address passed as an extra parameter}) and the location of any return value. If ABI information is not available a bit of lateral thinking might be needed to come up with an alternative output method.
I have not said anything about making use of signals and exception handling. These are hard enough to get right when documentation is available. The Turing machine theory folk usually skip over these real-world issues and I will join them for the time being.
Secret instruction sets about to make a come-back
Now it has happened Apple’s launch of a new processor, the A4, seems such an obvious thing to do. As the manufacturer of propriety products Apple wants to have complete control over the software that customers run on those products. Using a processor whose instruction set and electrical signals are not publicly available goes a very long way to ensuring that somebody else’s BIOS/OS/drivers/etc do not replace Apple’s or that the distributed software is not ‘usefully’ patched (Apple have yet to reveal their intentions on publishing instruction set details, this is an off-the-cuff prediction on my part).
Why are Apple funding the development of the LLVM C/C++ compiler? Because it enables them to write a back-end for the A4 without revealing the instruction set (using gcc for this purpose would require that the source be distributed, revealing the instruction set). So much for my prediction that Apple will stop funding LLVM.
The landscape of compute intensive cpus used to be populated with a wide variety of offerings from many manufacturers. The very high price of riding the crest of Moore’s law is one of the reasons that Intel’s x86 acquired such a huge chunk of this market; one by one processor companies decided not to make the investment needed to keep their products competitive. Now that the applicability of Moore’s law is drawing to an end the treadmill of continued processor performance upgrades is starting to fading away. Apple are not looking at a processor upgrade cycle, that they need to keep up with to be competitive, that stretches very far into the future.
Isn’t keeping an instruction set secret commercial suicide? The way to sell hardware is to make sure that lots of software runs on it and software developers want instruction set details (well ok, a small number do, but I’m sure lots of others get a warm fuzzy feeling knowing that the information is available should they need it). This is very much a last century view. The world is awash with an enormous variety of software, including lot of it very useful open source, and there is a lot more information available about the set of applications many customers want to use most of the time. Other than existing practice there is little reason why a manufacturer of a proprietary product, that is not a processor, needs to release instruction set details.
In the early 1980s I was at the technical launch of the Inmos Transputer and was told that the instruction set would not be published because the company did not want to be tied down to backwards compatibility. Perish the thought that customers would write assembler because the Inmos supplied compilers produced poor quality code or that a third party compiler would good enough to gain a significant market share. In marketing ability Inmos was the polar opposite of Apple. For a while HP were not very forthcoming on the instruction set behind their PA-RISC processor.
Will the A4 instruction set remain secret? On the whole, perhaps it can. The software based approaches to reverse engineering an instruction set require access to a compiler that generates it. For instance, changing a plus to a minus in one expression and looking for the small change in the generated executable; figuring out which status flags are set under which conditions is harder, but given time it can be done. Why would Apple release executable compilers if it wants to control the software that runs on the A4?
If the instruction set were cracked where would a developer go to obtain a compiler targeting the A4?
Given the FSF‘s history with Apple I would not be surprised if there was a fatwa against support for a proprietary instruction set in gcc. I suspect Apple would frown very heavily on such support ever being in the standard llvm distribution. I could see Apple’s lawyers sending letters to anybody making available a compiler that generated A4 code.
In the past manufacturers have tried to keep processor instruction sets secret and found that commercial reality required them to make this information freely available. Perhaps in the long term, like Moore’s law, the publication of detailed instruction set information may just be a passing phase.
Recent Comments