Archive
A safety-critical certification of the Linux kernel
This week there was an announcement on the system-safety mailing list that the Red Hat In-Vehicle Operating System (a version of the Linux kernel, plus a few subsystems) had been certified as being “… capable for use in ASIL B applications, …”. The Automotive Safety Integrity Levels (ASIL A is the lowest level, with D the highest; an example of ASIL B is controlling brake lights) are defined by ISO 26262, an international standard for functional safety of electrical and/or electronic systems installed in production road vehicles.
Given all I had heard about the problems that needed to be solved to get a safety certification for something as large and complicated as the Linux kernel, I wanted to know more about how Red Hat had achieved this certification.
The traditional, idealised, approach to certifying software is to check that all requirements are documented and traceable to the design, source code, tests, and test results. This information can be used to ensure that every requirement is implemented and produces the intended behavior, and that no undocumented functionality has been implemented.
When this approach is not practical (because of onerous time/cost), a potential get out of jail card is to use a Rigorous Development Process. Certification friendly development processes appear to revolve around lots of bureaucracy and following established buzzword techniques. The only development processes that have sometimes produced very reliable software all involve spending lots of time/money.
The major problems with certifying Linux are the apparent lack of specification/requirements documents, and a development process that does not claim to be rigorous.
The Red Hat approach is to treat the Linux man pages as the specification, extract the requirements from these pages, and then write the appropriate tests. Traceability looks like it is currently on the to-do list.
I have spent a lot of time working to understand specifications and their requirements; first with the C Standard and then with the Microsoft Server Protocols. This is the first time I have encountered man pages being used in a formal setting (sometimes they are used as one of the inputs to a reimplementation of a library).
Very little Open source software has a written specification in the traditional sense of a document cited in a contract that the vendor agrees to implement. Manuals, READMEs and help pages are not written in the formal style of a specification. A common refrain is that the source code is the specification. However, source is a specification of what the program does, it is not a specification of what the program is supposed to do.
The very nature of the Agile development process demands that there not be a complete specification. It’s possible that user stories could be treated as requirements.
There is an ISO Standard with Linux in its title: the Linux Base Standard. The goal of this Standard “… is to develop and promote a set of open standards that will increase compatibility among Linux distributions and enable software applications to run on any compliant system …”, i.e., it is not a specification of an OS kernel.
POSIX is a specification of the behavior of an OS (kernel functionality is specified by POSIX.1, .2 is shell and utilities, plus other .x documents). It’s many years since I tracked POSIX/Linux compliance, which was best described as “highly compatible”. Both Grok3 and ChatGPT o4 agree that “highly compatible” is still true, and list some known incompatibilities.
While they are not written in the form of a specification, the Linux man pages do have a consistent structure and are intended to be up-to-date. A person with a background of working with Linux kernels could probably extract meaningful requirements.
How many requirements are needed to cover the behavior of the Linux kernel?
On my computer running a 6.8.0-51 kernel, the /usr/include/linux directory contains 587 header files. Based on an analysis from 20 years ago (table 1897.1), most of these headers only declare macros and types (e.g., memory layout), not function declarations. The total number of function declarations in these headers is probably in the low thousands. POSIX (2008 version) defines 1,177 functions, but the number of system calls is probably around 300-400. Android implements 821 of these functions, of which 343 are system call related.
Let’s assume 2,000 functions. Some of these functions have an argument that specifies one or more optional values, each specifying a different sub-behavior. How many different sub-behaviors are there? If we assume that each kind of behavior is specified using a C macro, then Table 1897.1 suggests there might be around 10k C macros defined in these headers.
With positive/negative tests for each case, in round numbers we get (ignoring explicit testing of the values of struct members): 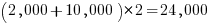 test files.
test files.
This calculation does not take into account combinations of options. I’m assuming that each test file will loop through various combinations of its kind of sub-behavior.
The 1990 C compiler validation suite contained around 1k tests. Thirty-five years later, 24k test files for a large OS feels low, but then combination testing should multiply the number of actual tests by at least an order of magnitude.
What is this hand-wavy analysis missing?
I suspect that the kernel is built with most of the optional functionality conditionally compiled out. This could significantly reduce the number of api functions and the supported options.
I have not taken into account any testing of the user-visible kernel data structures (because I don’t have any occurrence data).
Comments from readers with experience in testing OSes most welcome.
Another source of Linux specific information is the Linux Kernel documentation project. I don’t have any experience using this documentation, but the API documentation is very minimalist (automatically extracted from the source; the Assessment report lists this document as [D124], but never references it in the text).
Readers familiar with safety standards will be asking about the context in which this certification applies. Safety functions are not generic; they are specific to a safety-related system, i.e., software+hardware. This particular certification is for a Safety Element out of Context (SEooC), where “out of context” here means without the context of a system or knowledge of the safety goals. SEooC supports a bottom up approach to safety development, i.e., Safety Elements can be combined, along with the appropriate analysis and testing, to create a safety-related system.
This certification is the first of what I think will be many certifications of Linux, some at more rigorous safety levels.
Estimation experiments: specification wording is mostly irrelevant
Existing software effort estimation datasets provide information about estimates made within particular development environments and with particular aims. Experiments provide a mechanism for obtaining information about estimates made under conditions of the experimenters choice, at least in theory.
Writing the code is sometimes the least time-consuming part of implementing a requirement. At hackathons, my default estimate for almost any non-trivial requirement is a couple of hours, because my implementation strategy is to find the relevant library or package and write some glue code around it. In a heavily bureaucratic organization, the coding time might be a rounding error in the time taken up by meeting, documentation and testing; so a couple of months would be considered normal.
If we concentrate on the time taken to implement the requirements in code, then estimation time and implementation time will depend on prior experience. I know that I can implement a lexer for a programming language in half-a-day, because I have done it so many times before; other people take a lot longer because they have not had the amount of practice I have had on this one task. I’m sure there are lots of tasks that would take me many days, but there is somebody who can implement them in half-a-day (because they have had lots of practice).
Given the possibility of a large variation in actual implementation times, large variations in estimates should not be surprising. Does the possibility of large variability in subject responses mean that estimation experiments have little value?
I think that estimation experiments can provide interesting information, as long as we drop the pretence that the answers given by subjects have any causal connection to the wording that appears in the task specifications they are asked to estimate.
If we assume that none of the subjects is sufficiently expert in any of the experimental tasks specified to realistically give a plausible answer, then answers must be driven by non-specification issues, e.g., the answer the client wants to hear, a value that is defensible, a round number.
A study by Lucas Gren and Richard Berntsson Svensson asked subjects to estimate the total implementation time of a list of tasks. I usually ignore software engineering experiments that use student subjects (this study eventually included professional developers), but treating the experiment as one involving social processes, rather than technical software know-how, makes subject software experience a lot less relevant.
Assume, dear reader, that you took part in this experiment, saw a list of requirements that sounded plausible, and were then asked to estimate implementation time in weeks. What estimate would you give? I would have thrown my hands up in frustration and might have answered 0.1 weeks (i.e., a few hours). I expected the most common answer to be 4 weeks (the number of weeks in a month), but it turned out to be 5 (a very ‘attractive’ round number), for student subjects (code+data).
The professional subjects appeared to be from large organizations, who I assume are used to implementations including plenty of bureaucratic stuff, as well as coding. The task specification did not include enough detailed information to create an accurate estimate, so subjects either assumed their own work environment or played along with the fresh-faced, keen experimenter (sorry Lucas). The professionals showed greater agreement in that the range of value given was not as wide as students, but it had a more uniform distribution (with maximums, rather than peaks, at 4 and 7); see below. I suspect that answers at the high end were from managers and designers with minimal coding experience.
What did the experimenters choose weeks as the unit of estimation? Perhaps they thought this expressed a reasonable implementation time (it probably is if it’s not possible to use somebody else’s library/package). I think that they could have chosen day units and gotten essentially the same results (at least for student subjects). If they had chosen hours as the estimation unit, the spread of answers would have been wider, and I’m not sure whether to bet on 7 (hours in a working day) or 10 being the most common choice.
Fitting a regression model to the student data shows estimates increasing by 0.4 weeks per year of degree progression. I was initially baffled by this, and then I realized that more experienced students expect to be given tougher problems to solve, i.e., this increase is based on self-image (code+data).
The stated hypothesis investigated by the study involved none of the above. Rather, the intent was to measure the impact of obsolete requirements on estimates. Subjects were randomly divided into three groups, with each seeing and estimating one specification. One specification contained four tasks (A), one contained five tasks (B), and one contained the same tasks as (A) plus an additional task followed by the sentence: “Please note that R5 should NOT be implemented” (C).
A regression model shows that for students and professions the estimate for (A) is about 1-2 weeks lower than (B), while (A) estimates are 3-5 weeks lower than (C) estimated.
What are subjects to make of an experimental situation where the specification includes a task that they are explicitly told to ignore?
How would you react? My first thought was that the ignore R5 sentence was itself ignored, either accidentally or on purpose. But my main thought is that Relevance theory is a complicated subject, and we are a very long way away from applying it to estimation experiments containing supposedly redundant information.
The plot below shows the number of subjects making a given estimate, in days; exp0to2 were student subjects (dashed line joins estimate that include a half-hour value, solid line whole hour), exp3 MSc students, and exp4 professional developers (code+data):
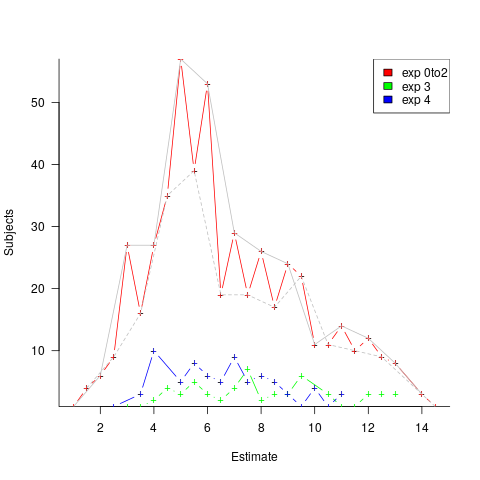
I hope that the authors of this study run more experiments, ideally working on the assumption that there is no connection between specification and estimate (apart from trivial examples).
Uncovering the undefined behaviors
I think that all programming languages contain some constructs that have undefined behavior.
The C Standard explicitly lists various constructs as having undefined behavior. It also specifies that: Undefined behavior is otherwise indicated in this International Standard by the words “undefined behavior” or by the omission of any explicit definition of behavior.; the second half of the sentence refers to what might be called implicit undefined behavior. Implicit undefined behavior can be subdivided into intentional and unintentional. Intentional undefined behavior applies to constructs that the committee considered and decided (and continues to decide) to say nothing about (e.g., question 19), while unintentional undefined behavior applies to constructs that the committee did not explicitly consider (when discovered, these often end up as defect reports, which are sometimes resolved as intentionally undefined behavior).
Fans of some languages claim that ‘their’ language does not contain any undefined behaviors.
Ada does not explicitly specify any construct as having undefined behavior, but it does specify that some constructs generate a bounded error; a rose by any other name…
I sometimes bump into language inventors claiming that ‘their’ language is fully specified, i.e., does not contain any undefined behaviors. My first question to them, about the behavior of division involving negative values, invariable requires me to explain that there are two possible ways of doing it (ignorance is bliss when fully specifying a language). The invariable answer is that the behavior is whatever the underlying implementation does (which is often written in C). In other words, they have imported all the undefined behaviors of the implementation language.
Follow-up question include: what is the order of expression evaluation (e.g., left-to-right, right-to-left, inside out…), what is the order of function argument evaluation (often driven by the direction of stack growth), what is the order of initialization and other order related questions that comes to mind. Their fully specified language quickly turns out to be a sham.
A recent post by John Regehr talks about Gödel’s incompleteness Theorem as a source of undefined behavior. My understanding is that the underlying argument is built on non-termination. How is it possible to tell the difference between non-termination and lasting longer than the age of the universe? In itself I don’t think this theorem is a source of undefined behavior; more enlightenment welcome.
Oh, I did not know that [about R]
I recently saw a post about something called ValidR and as somebody with a long standing professional interest in language validation immediately read the article and referenced links. I was disappointed to find that what was being validated was the installation, not the behavior of the implementation. In the context of what I understand ValidR’s target market to be, drug testing, obtaining reproducible results is very important and so it is necessary to know exact what software has been installed (e.g., packages and their versions).
Implementation validation involves checking that the implementation of a language adheres to the requirements specified in the appropriate language standard. While International standards exist for many of the widely used languages, some have standard’s developed through other means and some have no recognized specification at all (e.g., PHP, Perl and R).
Not having a recognized specification is a problem for PHP because there are multiple implementations in common use. Perl and R both have a dominant implementation, which means the definition of the language is accepted as being whatever that implementation does.
Now, anybody who claims that having an open source implementation is as good as having a specification written in English (i.e., people can read the code to discover the behavior) clearly have not done much, if any, reading of language implementations. Over the years I have worked with the source of a fare few language implementations and my general experience is that the fastest and most reliable way of finding out what an implementation does is to write test case, only reading the source when test cases cannot be found that answer the questions.
Does it matter that there is no complete English specification of R (the current specification is very much a work in progress, with lots of progress remaining)?
Who reads computer language specifications (apart from language wonks like me)? Creators of implementations is the most obvious answer. But an R implementation already exists, why should the R team spend time making it easier to create alternative implementations? Actually I see the main customers of an R language specification being the R-core team.
An example of the benefits to the owner of source code in having a specification is provided by the EU/Microsoft competition court case. I was an adviser to the Monitoring Trustee appointed by the Commission to oversee the documentation of the specification of these protocols (no previous documentation existed). A frequently heard comment from the senior Microsoft developers we dealt with, on reading their own new specifications, was “Oh, I did not know that”.
A written specification is much more compact than source code or test cases and is (or should be) organized in a way that helps readers understand what is being said (this is often a stated aim for source code but is rare achieved). There are probably lots of behaviors that the R team are unaware of which, if they get to find out about them, might be interested in ‘fixing’ or at least discussing whether it is a desirable behavior. Or perhaps the R team’s strategy is to make life difficult for competing implementations.
How many ways of programming the same specification?
How many different ways are there of writing a program to implement a given specification? Non-trivial specifications probably have an enormous number of possible programming solutions. What about really simple specifications, say something based on the 3n+1 problem (write a programs that takes a list of integers and outputs their ‘3n+1’ length; ‘3n+1’ length algorithm: for integer  , if
, if  is even divide it by
is even divide it by 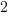 and assign the result to
and assign the result to  , otherwise
, otherwise  is odd, multiply it by
is odd, multiply it by 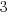 and add
and add 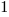 to give the new value of
to give the new value of  ; repeat the process, counting the number of iterations until
; repeat the process, counting the number of iterations until  reaches
reaches 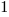 )?.
)?.
I can think of a dozen or so (slightly) different ways that I might write a program to solve this problem. If I really had to I could probably come up with a few hundred different solutions, but I think the source code of these programs would not look like something I would normally write. If I was to run a competition how many different answers might I get? If you twisted my arm I might have said 500. What do you think?
Meine van der Meulen studied the N-version programing for his PhD thesis (N groups independently write a program to the same specification, compare the output of the N programs and select the ‘best’ answer; cannot find a copy of the thesis online). This was empirical work and van der Meulen posted the above 3n+1 problem to a programming competition website and used the 95,497 submitted solutions for his analysis; he also kindly sent me a copy of the solutions (11,674 solutions were written in Pascal, the rest were in C).
Not all the solutions correctly solve the problem. I ignored this ‘detail’. There are also many duplicates (as in identical source code).
I am interested in differently coded solutions. I defined different as the sequence of operators/punctuators making up the program being different (or at least having a different MD5 checksum), so identifiers and comments are ignored. Should permutations in the order of independent adjacent statements really be counted as different? For the sack of keeping my life simple they current are. This definition of differently coded reduces the original 63,823 C programs down to 6,301. Wow, how are 6k+ different programs possible?
The original specification did not mention performance, but lots of developers did all sorts of weird and wonderful stuff to improve runtime performance. The most common optimization technique used (apart from some inventive ways of checking for odd/even) was to cache previous answers along with the solution for all the intermediate steps that were passed through on the way to 1 (the path from the starting value to 1 is very erratic and sometimes goes through values greater than the starting value) and check this cache to see whether it contains the current value of .
.
A common measure of program size is lines of code. What is the size distribution, in LOC, for these 6,301 programs? One program has been labeled an outlier and excluded from the analysis (most of its 8,345 lines were taken up with initializing a data structure with precomputed solutions).
The following plots lines of code against the number of programs containing that many lines (download code and data).
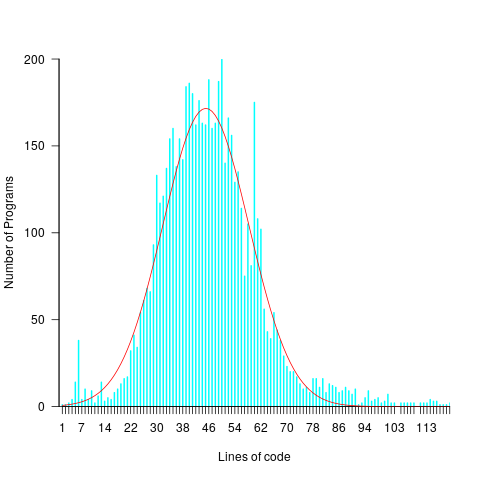
The mean program length is 46.3 lines, standard deviations 15.4. The red curve is a Normal distribution whose mean/sd has been tweaked to give a better visual fit (a Shapiro-Wilk test dispels any hope tht the distribution might be Normal). There is no reason to think that the data will be fitted by any known distribution and I’m not going to overfit on one data-point. If pushed I will wave my arms and describe the distribution as Normalish with added spikes and a fat right tail.
That spike around 60 lines is interesting. Is this group of solutions all doing the same thing but with different statement orderings? I have previously written about how gcc/llvm do a good job of turning the core of the algorithm into the same machine code. Perhaps a future version of these compilers will be able to tell us whether the programs clumping around 60 LOC are doing the same thing.
A change of guard in the C standard’s world?
I have just gotten back from the latest ISO C meeting (known as WG14 in the language standard’s world) which finished a whole day ahead of schedule; always a good sign that things are under control. Many of the 18 people present in London were also present when the group last met in London four years ago and if memory serves this same subset of people were also attending meetings 20 years ago when I traveled around the world as UK head of delegation (these days my enthusiasm to attend does not extend to leaving the country).
The current convenor, John Benito, is stepping down after 15 years and I suspect that many other active members will be stepping back from involvement once the current work on revising C99 is published as the new C Standard (hopefully early next year meaning it will probably be known as C12).
From the very beginning the active UK participants in WG14 have held one important point of view that has consistently been at odds with a view held by the majority of US participants; we in the UK have believed that it should be possible to deduce the requirements contained in the C Standard without reference to any deliberations of WG14, while many US participants have actively argued against what they see as over specification. I think one of the problems with trying to change US minds has been that the opinion leaders have been involved for so long and know the issues so well they cannot see how anybody could possible interpret wording in the standard in anything other than the ‘obvious’ way.
An example of the desire to not over specify is provided by a defect report I submitted 18 years ago, in particular question 19; what does:
#define f(a) a*g #define g(a) f(a) f(2)(9) |
expand to? There are two possibilities and WG14 came to the conclusion that both were valid macro expansions, making the behavior unspecified. However, when it came to a vote the consensus came down on the side of saying nothing about this case in the normative body of the standard, the only visible evidence for this behavior being a bulleted item added to the annex containing the list of unspecified behaviors.
A new member of WG14 (he has only been involved for a few years) spotted this bulleted item that had no corresponding text in the main body of the standard, tracked down the defect report that generated it and submitted a new defect report asking for wording to be added. At the meeting today the straw poll of those present was in favor of adding an appropriate example to C12 {I will link to the appropriate paper once it appears on the public WG14 site}. A minor victory on the road to a full and complete specification.
It will be interesting to see what impact a standing down of the old guard, after the publication of C12, has C2X (the revision of C that is likely to be published around 10 years from now).
For those of you still scratching their head, the two possibilities are:
2*f(9) |
or
2*9*g |
A fault in the C Standard or existing compilers?
Software is not the only entity that can contain faults. The requirements listed in a specification are usually considered to be correct, almost by definition. Of course the users of software implementing a specification may be unhappy with the behavior specified and wish that some alternative behavior occurred. A cut and dried fault occurs when two requirements conflict with each other.
The C Standard can be read as a specification for how C compilers should behave. Despite over 80 man years of effort and the continued scrutiny of developers over 20 years, faults continue to be uncovered. The latest potential fault (it is possible that the fault actually occurs in many existing compilers rather than the C Standard) was brought to my attention by Al Viro, one of the Sparse developers.
The issue involved the following code (which I believe the standard considers to be strictly conforming, but all the compilers I have tried disagree):
int (*f(int x))[sizeof x]; // A prototype declaration int (*g(int y))[sizeof y] // A function definition { return 0; } |
These function declarations are unusual in that their return type is a pointer to an array of integers, a type rarely encountered in this context (the original question involved a return type of pointer to function returning … and was more complicated).
The specific issue was the scope of the parameter (i.e., x and y), is the declaration still in scope at the point that the second occurrence of the identifier is encountered?
As a principle I think that the behavior, whatever it turns out to be, should be the same in both cases (neither the C standard or its rationale state such a principle).
Taking the function prototype case first:
The scope of the parameter x “… terminates at the end of the function declarator.” (sentence 409).
and does function prototype scope include the return type (the syntax calls the particular construct a declarator and there are at least two of them, one nested inside the other, in a function prototype declaration)?
Sentence 1592 says Yes, but sentence 279 and 1845 say No.
None of these references are normative references (standardize for definitive).
Moving on to the function definition case:
Where does the scope of the parameter x begin (sentence 418)?
“… scope that begins just after the completion of its declarator.”
and where does the scope end (sentence 408)?
“… which terminates at the end of the associated block.”
and what happens between the beginning and ending of the scope (sentence 412)?
“Within the inner scope, the identifier designates the entity declared in the inner scope;”
This looks very straight forward, there are no ‘gaps’ in the scope of the parameter definition appearing in a function definition. Consistency with the corresponding function prototype case requires that function declarator be interpreted to include the return type.
There is a related discussion involving a previous Defect Report 345 submitted a while ago.
The problem is that many existing compilers do not treat parameter scope in this way. They operate as-if there was a ‘gap’ in the parameter scope of function definition (probably because the code implementing this functionality is shared with that implementing function prototypes, which have been interpreted to not include the return type).
What happens next? Probably lots of discussion on the C Standard email reflector. Possible outcomes include somebody finding wording that requires a ‘gap’ in the scope of parameters in function definitions, it agreed that such a gap ought to be specified by the standard (because this is how existing code behaves because this is how compilers operate), or that the standard is correct as is and any compiler that behaves differently needs to be fixed.
Recent Comments