Archive
Extracting information from duplicate fault reports
Duplicate fault reports (that is, reports whose cause is the same underlying coding mistake) are an underused source of information. I sometimes email the authors of a paper analysing fault data asking for information about duplicates. Duplicate information is rarely available, because the authors don’t bother to record it.
If a program’s coding mistakes are a closed population, i.e., no new ones are added or existing ones fixed, duplicate counts might be used to estimate the number of remaining mistakes.
However, coding mistakes in production software systems are invariably open populations, i.e., reported faults are fixed, and new functionality (containing new coding mistakes) is added.
A dataset made available by Sadat, Bener, and Miranskyy contains 18 years worth of information on duplicate fault reports in Apache, Eclipse and KDE. The following analysis uses the KDE data.
Fault reports are created by users, and changes in the rate of reports whose root cause is the same coding mistake provides information on changes in the number of active users, or changes in the functionality executed by the active users. The plot below shows, for 10 unique faults (different colors), the number of days between the first report and all subsequent reports of the same fault (plus character); note the log scale y-axis (code+data):

Changes in the rate at which duplicates are reported are visible as changes in the slope of each line formed by plus signs of the respective color. Possible reasons for the change include: the coding mistake appears in a new release which users do not widely install for some time, 2) a fault become sufficiently well known, or workaround provided, that the rate of reporting for that fault declines. Of course, only some fault experiences are ever reported.
Almost all books/papers on software reliability that model the occurrence of fault experiences treat them as-if they were a Non-Homogeneous Poisson Process (NHPP); in most cases, authors are simply repeating what they have read elsewhere.
Some important assumptions made by NHPP models do not apply to software faults. For instance, NHPP models assume that the probability of encountering a fault experience is the same for different coding mistakes, i.e., they are all equally likely. What does the evidence show about this assumption? If all coding mistakes had the same probability of producing a fault experience, the mean time between duplicate fault reports would be the same for all fault reports. The plot below shows the interval, in days, between consecutive duplicate fault reports, for the 392 faults whose number of duplicates was between 20 and 100, sorted by interval (out of a total of 30,377; code+data):
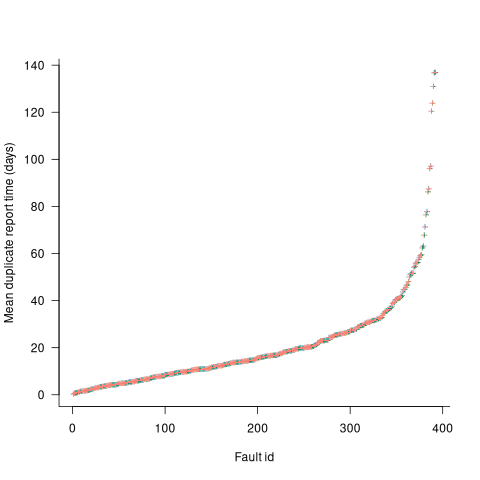
The variation in mean time between duplicate fault reports, for different faults, is evidence that different coding mistakes have different probabilities of producing a fault experience. This behavior is consistent with the observation that mistakes in deeply nested if-statements are less likely to be executed than mistakes contained in less-deeply nested code. However, this observation invalidating assumptions made by NHPP models has not prevented them dominating the research literature.
Some human biases in conditional reasoning
Tracking down coding mistakes is a common developer activity (for which training is rarely provided).
Debugging code involves reasoning about differences between the actual and expected output produced by particular program input. The goal is to figure out the coding mistake, or at least narrow down the portion of code likely to contain the mistake.
Interest in human reasoning dates back to at least ancient Greece, e.g., Aristotle and his syllogisms. The study of the psychology of reasoning is very recent; the field was essentially kick-started in 1966 by the surprising results of the Wason selection task.
Debugging involves a form of deductive reasoning known as conditional reasoning. The simplest form of conditional reasoning involves an input that can take one of two states, along with an output that can take one of two states. Using coding notation, this might be written as:
if (p) then q if (p) then !q if (!p) then q if (!p) then !q |
The notation used by the researchers who run these studies is a 2×2 contingency table (or conditional matrix):
OUTPUT
1 0
1 A B
INPUT
0 C D |
where: A, B, C, and D are the number of occurrences of each case; in code notation, p is the input and q the output.
The fertilizer-plant problem is an example of the kind of scenario subjects answer questions about in studies. Subjects are told that a horticultural laboratory is testing the effectiveness of 31 fertilizers on the flowering of plants; they are told the number of plants that flowered when given fertilizer (A), the number that did not flower when given fertilizer (B), the number that flowered when not given fertilizer (C), and the number that did not flower when not given any fertilizer (D). They are then asked to evaluate the effectiveness of the fertilizer on plant flowering. After the experiment, subjects are asked about any strategies they used to make judgments.
Needless to say, subjects do not make use of the available information in a way that researchers consider to be optimal, e.g., Allan’s 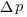 index
index  (sorry about the double,
(sorry about the double,  , rather than single, vertical lines).
, rather than single, vertical lines).
What do we know after 40+ years of active research into this basic form of conditional reasoning?
The results consistently find, for this and other problems, that the information A is given more weight than B, which is given by weight than C, which is given more weight than D.
That information provided by A and B is given more weight than C and D is an example of a positive test strategy, a well-known human characteristic.
Various models have been proposed to ‘explain’ the relative ordering of information weighting: 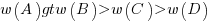 , e.g., that subjects have a bias towards sufficiency information compared to necessary information.
, e.g., that subjects have a bias towards sufficiency information compared to necessary information.
Subjects do not always analyse separate contingency tables in isolation. The term blocking is given to the situation where the predictive strength of one input is influenced by the predictive strength of another input (this process is sometimes known as the cue competition effect). Debugging is an evolutionary process, often involving multiple test inputs. I’m sure readers will be familiar with the situation where the output behavior from one input motivates a misinterpretation of the behaviour produced by a different input.
The use of logical inference is a commonly used approach to the debugging process (my suggestions that a statistical approach may at times be more effective tend to attract odd looks). Early studies of contingency reasoning were dominated by statistical models, with inferential models appearing later.
Debugging also involves causal reasoning, i.e., searching for the coding mistake that is causing the current output to be different from that expected. False beliefs about causal relationships can be a huge waste of developer time, and research on the illusion of causality investigates, among other things, how human interpretation of the information contained in contingency tables can be ‘de-biased’.
The apparently simple problem of human conditional reasoning over two variables, each having two states, has proven to be a surprisingly difficult to model. It is tempting to think that the performance of professional software developers would be closer to the ideal, compared to the typical experimental subject (e.g., psychology undergraduates or Mturk workers), but I’m not sure whether I would put money on it.
Cost-effectiveness decision for fixing a known coding mistake
If a mistake is spotted in the source code of a shipping software system, is it more cost-effective to fix the mistake, or to wait for a customer to report a fault whose root cause turns out to be that particular coding mistake?
The naive answer is don’t wait for a customer fault report, based on the following simplistic argument: 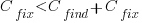 .
.
where: 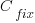 is the cost of fixing the mistake in the code (including testing etc), and
is the cost of fixing the mistake in the code (including testing etc), and 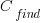 is the cost of finding the mistake in the code based on a customer fault report (i.e., the sum on the right is the total cost of fixing a fault reported by a customer).
is the cost of finding the mistake in the code based on a customer fault report (i.e., the sum on the right is the total cost of fixing a fault reported by a customer).
If the mistake is spotted in the code for ‘free’, then 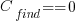 , e.g., a developer reading the code for another reason, or flagged by a static analysis tool.
, e.g., a developer reading the code for another reason, or flagged by a static analysis tool.
This answer is naive because it fails to take into account the possibility that the code containing the mistake is deleted/modified before any customers experience a fault caused by the mistake; let 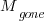 be the likelihood that the coding mistake ceases to exist in the next unit of time.
be the likelihood that the coding mistake ceases to exist in the next unit of time.
The more often the software is used, the more likely a fault experience based on the coding mistake occurs; let 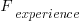 be the likelihood that a fault is reported in the next time unit.
be the likelihood that a fault is reported in the next time unit.
A more realistic analysis takes into account both the likelihood of the coding mistake disappearing and a corresponding fault being reported, modifying the relationship to: 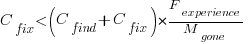
Software systems are eventually retired from service; the likelihood that the software is maintained during the next unit of time, 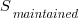 , is slightly less than one.
, is slightly less than one.
Giving the relationship: 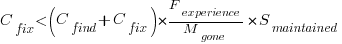
which simplifies to: 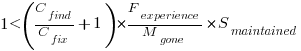
What is the likely range of values for the ratio: 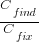 ?
?
I have no find/fix cost data, although detailed total time is available, i.e., find+fix time (with time probably being a good proxy for cost). My personal experience of find often taking a lot longer than fix probably suffers from survival of memorable cases; I can think of cases where the opposite was true.
The two values in the ratio 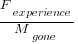 are likely to change as a system evolves, e.g., high code turnover during early releases that slows as the system matures. The value of
are likely to change as a system evolves, e.g., high code turnover during early releases that slows as the system matures. The value of 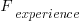 should decrease over time, but increase with a large influx of new users.
should decrease over time, but increase with a large influx of new users.
A study by Penta, Cerulo and Aversano investigated the lifetime of coding mistakes (detected by several tools), tracking them over three years from creation to possible removal (either fixed because of a fault report, or simply a change to the code).
Of the 2,388 coding mistakes detected in code developed over 3-years, 41 were removed as reported faults and 416 disappeared through changes to the code: 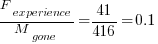
The plot below shows the survival curve for memory related coding mistakes detected in Samba, based on reported faults (red) and all other changes to the code (blue/green, code+data):
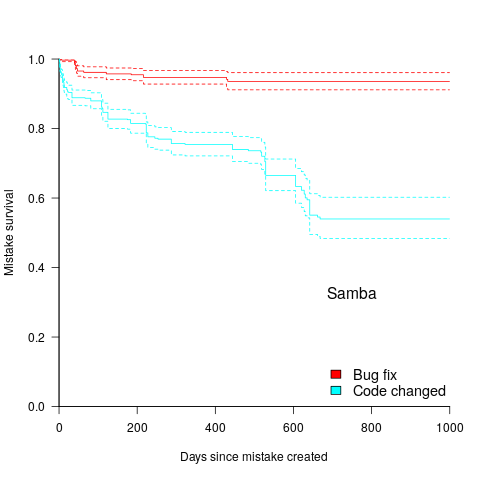
Coding mistakes are obviously being removed much more rapidly due to changes to the source, compared to customer fault reports.
For it to be cost-effective to fix coding mistakes in Samba, flagged by the tools used in this study (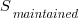 is essentially one), requires:
is essentially one), requires: 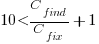 .
.
Meeting this requirement does not look that implausible to me, but obviously data is needed.
Mutation testing: its days in the limelight are over
How good a job does a test suite do in detecting coding mistakes in the program it tests?
Mutation testing provides one answer to this question. The idea behind mutation testing is to make a small change to the source code of the program under test (i.e., introduce a coding mistake), and then run the test suite through the mutated program (ideally one or more tests fail, as-in different behavior should be detected); rinse and repeat. The mutation score is the percentage of mutated programs that cause a test failure.
While Mutation testing is 50-years old this year (although the seminal paper did not get published until 1978), the computing resources needed to research it did not start to become widely available until the late 1980s. From then, until fuzz testing came along, mutation testing was probably the most popular technique studied by testing researchers. A collected bibliography of mutation testing lists 417 papers and 16+ PhD thesis (up to May 2014).
Mutation testing has not been taken up by industry because it tells managers what they already know, i.e., their test suite is not very good at finding coding mistakes.
Researchers concluded that the reason industry had not adopted mutation testing was that it was too resource intensive (i.e., mutate, compile, build, and run tests requires successively more resources). If mutation testing was less resource intensive, then industry would use it (to find out faster what they already knew).
Creating a code mutant is not itself resource intensive, e.g., randomly pick a point in the source and make a random change. However, the mutated source may not compile, or the resulting mutant may be equivalent to one created previously (e.g., the optimised compiled code is identical), or the program takes ages to compile and build; techniques for reducing the build overhead include mutating the compiler intermediate form and mutating the program executable.
Some changes to the source are more likely to be detected by a test suite than others, e.g., replacing <= by > is more likely to be detected than replacing it by < or ==. Various techniques for context dependent mutations have been proposed, e.g., handling of conditionals.
While mutation researchers were being ignored by industry, another group of researchers were listening to industry's problems with testing; automatic test case generation took off. How might different test case generators be compared? Mutation testing offers a means of evaluating the performance of tools that arrived on the scene (in practice, many researchers and tool vendors cite statement or block coverage numbers).
Perhaps industry might have to start showing some interest in mutation testing.
A fundamental concern is the extent to which mutation operators modify source in a way that is representative of the kinds of mistakes made by programmers.
The competent programmer hypothesis is often cited, by researchers, as the answer to this question. The hypothesis is that competent programmers write code/programs that is close to correct; the implied conclusion being that mutations, which are small changes, must therefore be like programmer mistakes (the citation often given as the source of this hypothesis discusses data selection during testing, but does mention the term competent programmer).
Until a few years ago, most analysis of fixes of reported faults looked at what coding constructs were involved in correcting the source code, e.g., 296 mistakes in TeX reported by Knuth. This information can be used to generate a probability table for selecting when to mutate one token into another token.
Studies of where the source code was changed, to fix a reported fault, show that existing mutation operators are not representative of a large percentage of existing coding mistakes; for instance, around 60% of 290 source code fixes to AspectJ involved more than one line (mutations usually involve a single line of source {because they operate on single statements and most statements occupy one line}), another study investigating many more fixes found only 10% of fixes involved one line, and similar findings for a study of C, Java, Python, and Haskell (a working link to the data, which is a bit disjointed of a mess).
These studies, which investigated the location of all the source code that needs to be changed, to fix a mistake, show that existing mutation operators are not representative of most human coding mistakes. To become representative, mutation operators need to be capable of making coupled changes across multiple lines/functions/methods and even files.
While arguments over the validity of the competent programmer hypothesis rumble on, the need for multi-line changes remains.
Given the lack of any major use-cases for mutation testing, it does not look like it is worth investing lots of resources on this topic. Researchers who have spent a large chunk of their career working on mutation testing will probably argue that you never know what use-cases might crop up in the future. In practice, mutation research will probably fade away because something new and more interesting has come along, i.e., fuzz testing.
There will always be niche use-cases for mutation. For instance, how likely is it that a random change to the source of a formal proof will go unnoticed by its associated proof checker (i.e., the proof checking tool output remains unchanged)?
A study based on mutating the source of Coq verification projects found that 7% of mutations had no impact on the results.
Increase in defect fixing costs with distance from original mistake
During software development, when a mistake has been made it may be corrected soon after it is made, much later during development, by the customer in a shipped product, or never corrected.
If a mistake is corrected, the cost of correction increases as the ‘distance’ between its creation and detection increases. In a phased development model, the distance might be the number of phases between creation and detection; in a throw it at the wall and see if it sticks development model, the distance might be the number of dependencies on the ‘mistake’ code.
There are people who claim that detecting mistakes earlier will save money. This claim overlooks the cost of detecting mistakes, and in some cases earlier detection is likely to be more expensive (or the distribution of people across phases may rate limit what can be done in any phase). For instance, people might not be willing to read requirements documents, but be willing to try running software; some coding mistakes are only going to be encountered later during integration test, etc.
Folklore claims of orders of magnitude increases in fixing cost, as ‘distance’ increases, have been shown to be hand waving.
I know of two datasets on ‘distance’ between mistake creation and detection. A tiny dataset in Implementation of Fault Slip Through in Design Phase of the Project (containing only counts information; also see figure 6.41), and the CESAW dataset.
The plot below shows the time taken to fix 7,000 reported defects by distance between phases, for CESAW project 615 (code+data). The red lines are fitted regression models of the form 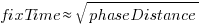 , for minimum fix times of 1, 5 and 10 minutes:
, for minimum fix times of 1, 5 and 10 minutes:
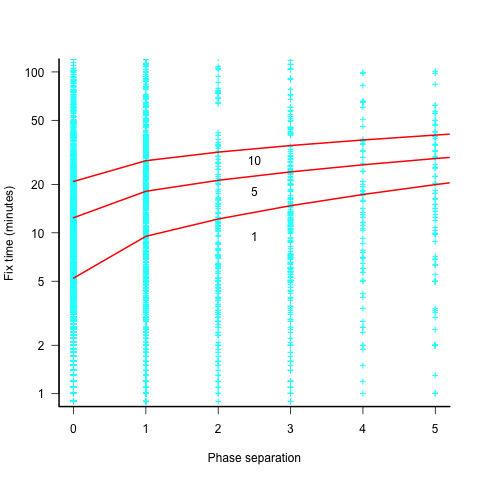
The above plot makes various simplifying assumptions, including: ‘sub-phases’ being associated with a ‘parent’ phase selected by your author, and the distance between all pairs of adjacent phase is the same (in terms of their impact on fix time).
A more sophisticated data model might change the functional form of the fitted regression model, but is unlikely to remove the general upward trend.
There are lots of fix times taking less than five minutes. Project 615 developed safety critical software, and so every detected mistake was recorded; on other projects, small mistakes would probably been fixed without an associated formal record.
I think that, if it were not for the, now discredited, folklore claiming outsized relative costs for fixing reported defects at greater ‘distances’ from the introduction of a mistake, this issue would be a niche topic.
Likelihood of a fault experience when using the Horizon IT system
It looks like the UK Post Office’s Horizon IT system is going to have a significant impact on the prosecution of cases that revolve around the reliability of software systems, at least in the UK. I have discussed the evidence illustrating the fallacy of the belief that “most computer error is either immediately detectable or results from error in the data entered into the machine.” This post discusses what can be learned about the reliability of a program after a fault experience has occurred, or alleged to have occurred in the Horizon legal proceedings.
Sub-postmasters used the Horizon IT system to handle their accounts with the Post Office. In some cases money that sub-postmasters claimed to have transferred did not appear in the Post Office account. The sub-postmasters claimed this was caused by incorrect behavior of the Horizon system, the Post Office claimed it was due to false accounting and prosecuted or fired people and sometimes sued for the ‘missing’ money (which could be in the tens of thousands of pounds); some sub-postmasters received jail time. In 2019 a class action brought by 550 sub-postmasters was settled by the Post Office, and the presiding judge has passed a file to the Director of Public Prosecutions; the Post Office may be charged with instituting and pursuing malicious prosecutions. The courts are working their way through reviewing the cases of the sub-postmasters charged.
How did the Post Office lawyers calculate the likelihood that the missing money was the result of a ‘software bug’?
Horizon trial transcript, day 1, Mr De Garr Robinson acting for the Post Office: “Over the period 2000 to 2018 the Post Office has had on average 13,650 branches. That means that over that period it has had more than 3 million sets of monthly branch accounts. It is nearly 3.1 million but let’s call it 3 million and let’s ignore the fact for the first few years branch accounts were weekly. That doesn’t matter for the purposes of this analysis. Against that background let’s take a substantial bug like the Suspense Account bug which affected 16 branches and had a mean financial impact per branch of £1,000. The chances of that bug affecting any branch is tiny. It is 16 in 3 million, or 1 in 190,000-odd.”
That 3.1 million comes from the calculation: 19-year period times 12 months per year times 13,650 branches.
If we are told that 16 events occurred, and that there are 13,650 branches and 3.1 million transactions, then the likelihood of a particular transaction being involved in one of these events is 1 in 194,512.5. If all branches have the same number of transactions, the likelihood of a particular branch being involved in one of these 16 events is 1 in 853 (13650/16 -> 853); the branch likelihood will be proportional to the number of transactions it performs (ignoring correlation between transactions).
This analysis does not tell us anything about the likelihood that 16 events will occur, and it does not tell us anything about whether these events are the result of a coding mistake or fraud.
We don’t know how many of the known 16 events are due to mistakes in the code and how many are due to fraud. Let’s ask: What is the likelihood of one fault experience occurring in a software system that processes a total of 3.1 million transactions (the number of branches is not really relevant)?
The reply to this question is that it is not possible to calculate an answer, because all the required information is not specified.
A software system is likely to contain some number of coding mistakes, and given the appropriate input, any of these mistakes may produce a fault experience. The information needed to calculate the likelihood of one fault experience occurring is:
- the number of coding mistakes present in the software system,
- for each coding mistake, the probability that an input drawn from the distribution of input values produced by users of the software will produce a fault experience.
Outside of research projects, I don’t know of any anyone who has obtained the information needed to perform this calculation.
The Technical Appendix to Judgment (No.6) “Horizon Issues” states that there were 112 potential occurrences of the Dalmellington issue (paragraph 169), but does not list the number of transactions processed between these ‘issues’ (which would enable a likelihood to be estimated for that one coding mistake).
The analysis of the Post Office expert, Dr Worden, is incorrect in a complicated way (paragraphs 631 through 635). To ‘prove’ that the missing money was very unlikely to be the result of a ‘software bug’, Dr Worden makes a calculation that he claims is the likelihood of a particular branch experiencing a ‘bug’ (he makes the mistake of using the number of known events, not the number of unknown possible events). He overlooks the fact that while the likelihood of a particular branch experiencing an event may be small, the likelihood of any one of the branches experiencing an event is 13,630 times higher. Dr Worden’s creates complication by calculating the number of ‘bugs’ that would have to exist for there to be a 1 in 10 chance of a particular branch experiencing an event (his answer is 50,000), and then points out that 50,000 is such a large number it could not be true.
As an analogy, let’s consider the UK National Lottery, where the chance of winning the Thunderball jackpot is roughly 1 in 8-million per ticket purchased. Let’s say that I bought a ticket and won this week’s jackpot. Using Dr Worden’s argument, the lottery could claim that my chance of winning was so low (1 in 8-million) that I must have created a counterfeit ticket; they could even say that because I did not buy 0.8 million tickets, I did not have a reasonable chance of winning, i.e., a 1 in 10 chance. My chance of winning from one ticket is the same as everybody else who buys one ticket, i.e., 1 in 8-million. If millions of tickets are bought, it is very likely that one of them will win each week. If only, say, 13,650 tickets are bought each week, the likelihood of anybody winning in any week is very low, but eventually somebody will win (perhaps after many years).
The difference between the likelihood of winning the Thunderball jackpot and the likelihood of a Horizon fault experience is that we have enough information to calculate one, but not the other.
The analysis by the defence team produced different numbers, i.e., did not conclude that there was not enough information to perform the calculation.
Is there any way that the information needed to calculate the likelihood of a fault experience occurring?
In theory fuzz testing could be used. In practice this is probably completely impractical. Horizon is a data driven system, and so a copy of the database would need to be used, along with a copy of all the Horizon software. Where is the computer needed to run this software+database? Yes, use of the Post Office computer system would be needed, along with all the necessary passwords.
Perhaps, if we wait long enough, a judge will require that one party make all the software+database+computer+passwords available to the other party.
Impact of function size on number of reported faults
Are longer functions more likely to contain more coding mistakes than shorter functions?
Well, yes. Longer functions contain more code, and the more code developers write the more mistakes they are likely to make.
But wait, the evidence shows that most reported faults occur in short functions.
This is true, at least in Java. It is also true that most of a Java program’s code appears in short methods (in C 50% of the code is contained in functions containing 114 or fewer lines, while in Java 50% of code is contained in methods containing 4 or fewer lines). It is to be expected that most reported faults appear in short functions. The plot below shows, left: the percentage of code contained in functions/methods containing a given number of lines, and right: the cumulative percentage of lines contained in functions/methods containing less than a given number of lines (code+data):
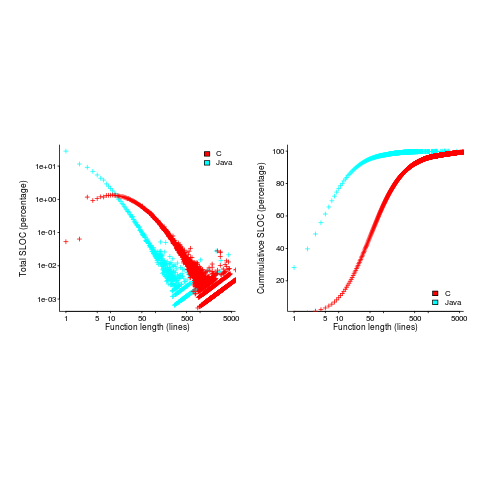
Does percentage of program source really explain all those reported faults in short methods/functions? Or are shorter functions more likely to contain more coding mistakes per line of code, than longer functions?
Reported faults per line of code is often referred to as: defect density.
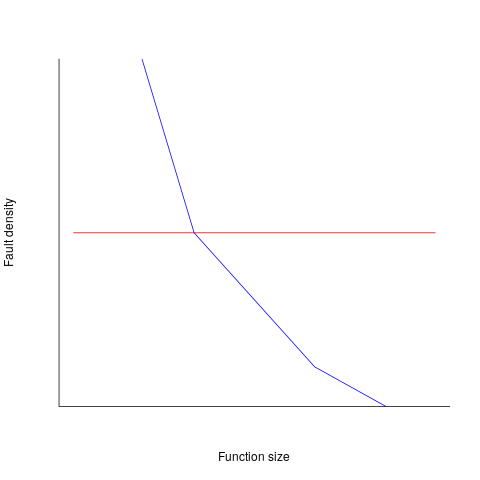
If defect density was independent of function length, the plot of reported faults against function length (in lines of code) would be horizontal; red line below. If every function contained the same number of reported faults, the plotted line would have the form of the blue line below.
Two things need to occur for a fault to be experienced. A mistake has to appear in the code, and the code has to be executed with the ‘right’ input values.
Code that is never executed will never result in any fault reports.
In a function containing 100 lines of executable source code, say, 30 lines are rarely executed, they will not contribute as much to the final total number of reported faults as the other 70 lines.
How does the average percentage of executed LOC, in a function, vary with its length? I have been rummaging around looking for data to help answer this question, but so far without any luck (the llvm code coverage report is over all tests, rather than per test case). Pointers to such data very welcome.
Statement execution is controlled by if-statements, and around 17% of C source statements are if-statements. For functions containing between 1 and 10 executable statements, the percentage that don’t contain an if-statement is expected to be, respectively: 83, 69, 57, 47, 39, 33, 27, 23, 19, 16. Statements contained in shorter functions are more likely to be executed, providing more opportunities for any mistakes they contain to be triggered, generating a fault experience.
Longer functions contain more dependencies between the statements within the body, than shorter functions (I don’t have any data showing how much more). Dependencies create opportunities for making mistakes (there is data showing dependencies between files and classes is a source of mistakes).
The previous analysis makes a large assumption, that the mistake generating a fault experience is contained in one function. This is true for 70% of reported faults (in AspectJ).
What is the distribution of reported faults against function/method size? I don’t have this data (pointers to such data very welcome).
The plot below shows number of reported faults in C++ classes (not methods) containing a given number of lines (from a paper by Koru, Eman and Mathew; code+data):
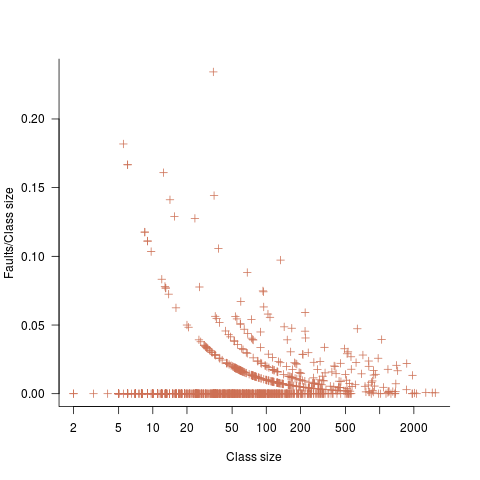
It’s tempting to think that those three curved lines are each classes containing the same number of methods.
What is the conclusion? There is one good reason why shorter functions should have more reported faults, and another good’ish reason why longer functions should have more reported faults. Perhaps length is not important. We need more data before an answer is possible.
Time-to-fix when mistake discovered in a later project phase
Traditionally the management of software development projects divides them into phases, e.g., requirements, design, coding and testing. A mistake introduced in one phase may not be detected until a later phase. There is long-standing folklore that earlier mistakes detected in later phases are much much more costly to fix persists, despite the original source of this folklore being resoundingly debunked. Fixing a mistake later is likely to a bit more costly, but how much more costly? A lack of data prevents reliable analysis; this question also suffers from different projects having different cost-to-fix profiles.
This post addresses the time-to-fix question (cost involves all the resources needed to perform the fix). Does it take longer to correct mistakes when they are detected in phases that come after the one in which they were made?
The data comes from the paper: Composing Effective Software Security Assurance Workflows. The 35,367 (yes, thirty-five thousand) logged fixes, from 39 projects drawn from three organizations, contains information on: phases in which the mistake was made and fixed, time taken, person ID, project ID, date/time, plus other stuff 🙂
Every project has its own characteristics that affect time-to-fix. Project 615, avionics software developed by organization A, has the most fixes (7,503) and is analysed here.
Avionics software is safety critical, and each major phase included its own review and inspection. The major phases include: requirements gathering, requirements analysis, high level design, design, coding, and testing. When counting the number of phases between introduction/fix, should review and inspection each count as a phase?
The primary reason for doing a review and inspection is to check the correctness (i.e., lack of mistakes) in the corresponding phase. If there is a time-to-fix penalty for mistakes found in these symbiotic-phases, I suspect it will be different from the time-to-fix penalty between major phases (which for simplicity, I’m assuming is major-phase independent).
The time-to-fix has a resolution of 1-minute, and some fix times are listed as taking a minute; 72% of fixes are recorded as taking less than 10-minutes. What kind of mistakes require less than 10-minutes to fix? Typos and other minutiae.
The plot below shows time-to-fix for mistakes having a given ‘distance’ between introduction/fix phase, for fixes taking at least 1, 5 and 10-minutes (code+data):
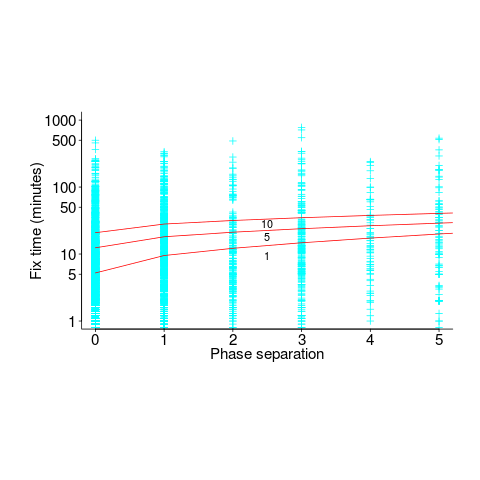
There is a huge variation in time-to-fix, and the regression lines (which have the form: 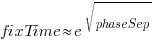 ) explains just 6% of the variance in the data, i.e., there is a small increase with phase separation, but it is almost down in the noise.
) explains just 6% of the variance in the data, i.e., there is a small increase with phase separation, but it is almost down in the noise.
All but one of the 38 people who worked on the project made multiple fixes (30 made more than 20 fixes), and may have got faster with practice. Adding the number of previous fixes by people making more than 20 fixes to the model gives: 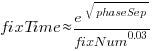 , and improves the model by less than 1-percent.
, and improves the model by less than 1-percent.
Fixing mistakes is a human activity, and individual performance often has a big impact on fitted models. Adding person ID to the model as a multiplication factor: i.e., 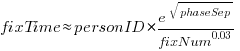 , improves the variance explained to 14% (better than a poke in the eye, just). The fitted value of
, improves the variance explained to 14% (better than a poke in the eye, just). The fitted value of 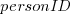 varies between 0.66 and 1.4 (factor of two, human variation).
varies between 0.66 and 1.4 (factor of two, human variation).
The answer to the time-to-fix question posed earlier (for project 615), is that it does take slightly longer to fix a mistake detected in phases occurring after the one in which the mistake was introduced. The phase difference is tiny, with differences in human performance having a bigger impact.
I made a mistake, please don’t shoot me
The major difference between commercial/academic written software is the handling of user mistakes, or to be more exact what is considered to be a user mistake. In the commercial world the emphasis is on keeping the customer happy, which translates into trying hard to gracefully handle any ‘mistake’ the user makes. Academic software is generally written to solve a research problem and is often very unforgiving of users failing to keep to the undocumented straight and narrow; given the context this unforgiving behavior is understandable, but sometimes such software is released to an unsuspecting world.
The R archive of contributed packages, CRAN, is a good example of the academic approach to writing software. I am an active user of many packages in this archive and its contributors have my heart-felt thanks. But on a regular basis I make a mistake when calling a function in one of these packages, get shot in the foot and am not best pleased.
What makes the situation worse is that my mistakes are often so trivial and easy to fix (by both me or the package authors). My most common ‘mistake’ is passing an argument whose type is not handled by the function, e.g., passing a data-frame to diag (why do I have to convert the argument using as.matrix, when diag could spot my mistake and do the conversion for me instead of returning some horrible mess).
Commercial software can also be unforgiving of user mistakes; in fact early versions of a lot of commercial software is just as unfriendly as academic software. The difference is that the commercial managers will make it their business to ensure that developers fix the code to make it user friendly. Competition ensures that those who don’t listen to their users go out of business.
Updating code to gracefully handle user mistakes is often a chore and many developers hate having to do it, managers are needed to prod developers into doing the work. The only purpose for more than half of the code in a commercial product may be to handle user mistakes and the percentage can approach 90%.
A lot of Open Source software has significant commercial backing, e.g., Linux, Apache, Firefox and gcc/llvm, which means it is somebody’s job to make sure customer complaints are addressed.
What the R development team needs is more commercial backing (it appears to have very little, but I may be wrong). Then somebody can be hired to go through the popular packages to make then mistake friendly, feed the changes back to the original author and generally educate package developers about bullet proofing their code.
Never too experienced to make a basic mistake
I was one of the 170 or so people at the Data Science hackathon in London over the weekend. As always this was well run by Carlos and his team who kept us fed, watered and connected to the Internet.
One of the three challenges involved a dataset containing pairs of Twitter users, A and B, where one of the pair had been ranked, by a person, as more influential than the other (the data was provided by PeerIndex, an event sponsor). The dataset contained 22 attributes, 11 for each user of the pair, plus 0/1 to indicate who was most influential; there was a training dataset of 5.5K pairs to learn against and a test dataset to make predictions against. The data was not messy or even sparse, how hard could it be?
Talks had been organized for the morning and afternoon. While Microsoft (one of the event sponsors) told us about Azure and F#, I sat at the back trying out various machine learning packages. Yes, the technical evangelists told us, Linux as well as Windows instances were available in Azure, support was available for the usual big data languages (e.g., Python and R; the Microsoft people seemed to be much more familiar with Python) plus dot net (this was the first time I had heard the use of dot net proposed as a big data solution for the Cloud).
Some members of Team Outliers from previous hackathons (Jonny, Bob and me) formed a team and after the talks had finished the Microsoft people+partners sat at our table (probably because our age distribution was similar to theirs, i.e., at the opposite end of the range to most teams; some of the Microsoft people got very involved in trying to produce a solution to the visualization challenge).
Integrating F# with bigdata seems to involve providing an interface to R packages (this is done by interfacing to the packages installed on a local R installation) and getting the IDE to know about the names of columns contained in data that has been read. Since I think the world needs new general purpose programming languages as much as it needs holes in the head I won’t say any more.
When in challenge solving mode I was using cross-validation to check the models being built and scoring around 0.76 (AUC, the metric used by the organizers). Looking at the leader board later in the afternoon showed several teams scoring over 0.85, a big difference; what technique were they using to get such a big improvement?
A note: even when trained on data that uses 0/1 predictor values machine learners don’t produce models that return zero or one, many return values in the range 0..1 (some use other ranges) and the usual technique is treat all values greater than 0.5 as a 1 (or TRUE or ‘yes’, etc) and all other values as a 0 (or FALSE or ‘no’, etc). This (x > 0.5) test had to be done to cross validate models using the training data and I was using the same technique for the test data. With an hour to go in the 24 hour hackathon we found out (change from ‘I’ to ‘we’ to spread the mistake around) that the required test data output was a probability in the range 0..1, not just a 0/1 value; the example answer had this behavior and this requirement was explained in the bottom right of the submission page! How many times have I told others to carefully read the problem requirements? Thankfully everybody was tired and Jonny&Bob did not have the energy to throw me out of the window for leading them so badly astray.
Having AUC as the metric should have raised a red flag, this does not make much sense for a 0/1 answer; using AUC makes sense for PeerIndex because they will want to trade off recall/precision. Also, its a good idea to remove ones ego when asked the question: are lots of people doing something clever or are you doing something stupid?
While we are on the subject of doing the wrong thing, one of the top three teams gave an excellent example of why sales/marketing don’t like technical people talking to clients. Having just won a prize donated by Microsoft for an app using Azure, the team proceeded to give a demo and explain how they had done everything using Google services and made it appear within a browser frame as if it were hosted on Azure. A couple of us sitting at the back were debating whether Microsoft would jump in and disqualify them.
What did I learn that I did not already know this weekend? There are some R machine learning packages on CRAN that don’t include a predict function (there should be a research-only subsection on CRAN for packages like this) and some ranking algorithms need more than 6G of memory to process 5.5K pairs.
There seemed to be a lot more people using Python, compared to R. Perhaps having the sample solution in Python pushed the fence sitters that way. There also seemed to be more women present, but that may have been because there were more people at this event than previous ones and I am responding to absolute numbers rather than percentage.
Recent Comments