Archive
Half-life of Microsoft products is 7 years
I get a lot of pushback from developers/managers when I tell them that the average application has a relatively short lifetime, i.e., half-life of 4-8 years. The pushback kicks in when I start citing data, up until then my listeners appear surprised/skeptical. The fact that source code has a brief and lonely existence is accepted, but telling them about the (one study) evidence that a coding mistake is more likely to disappear because of an unrelated coding change than as a result of fixing a fault report appears to make them feel uncomfortable.
Some applications live a long time, and most developers will spend most of their time working on long-lived applications. Short-lived applications are not around long enough to acquire significant developer/manager mind share.
I think the pushback is rooted in more than developer experience; developers don’t like the thought of their work disappearing from the world. The desire for permanence in what we create may be a human characteristic. Extolling the creation of reliable, maintainable, readable code creates an implicit assumption that applications are going to live long enough for the cost of these activities to be paid back.
How accurate are these half-life estimates?
The 4-8 year half-life range is derived from two datasets. A while ago I spotted another dataset: Fabiano Riccardi‘s Killed by Microsoft, currently containing information on 141 killed products.
All three datasets list just the products that have been killed, i.e., they are not a list of all products. A half-life calculation based only on killed products could underestimate the actual lifetime, it depends on whether the rate of killed products remains roughly the same percentage of all products or not. If the number of products killed, in any period, is always roughly the same percentage of all current products, then the calculated lifetime is not affected by the lack of data on the number of live products. Uncertainty in the calculated lifetime is created when the number of products killed is unconnected with the current number of live products.
It’s possible, to save money, products are more likely to be killed when a company is going through a period of poor performance, or the economy is in recession, compared to when business is booming.
Another source of uncertainty is sampling bias. Companies announce when products are released/withdrawn, creating recency bias because it’s easier to monitor the news than actively search for data on past product releases/withdraws. The plot below shows the number of products Microsoft killed in each year (red bars; post 2025 are to be killed-by dates) and number of new products launched each year blue/green line (code+data):
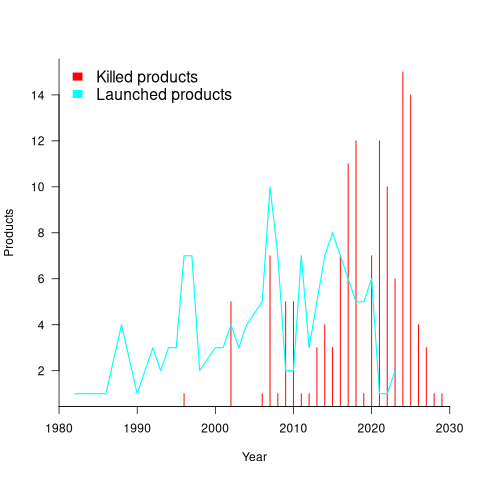
I’m sure that Microsoft killed more than one product before 2000. The Dot-com bubble burst in March 2000, and I would expect this to have resulted in lots of killed products. The lack of data on products killed before 2000 means that shorter lived products are undercounted.
The plot below shows the number of Microsoft (eventually killed) products still supported a given number of years after launch, the red line is a regression fit for products aged between 4 months and 22 years (code+data):
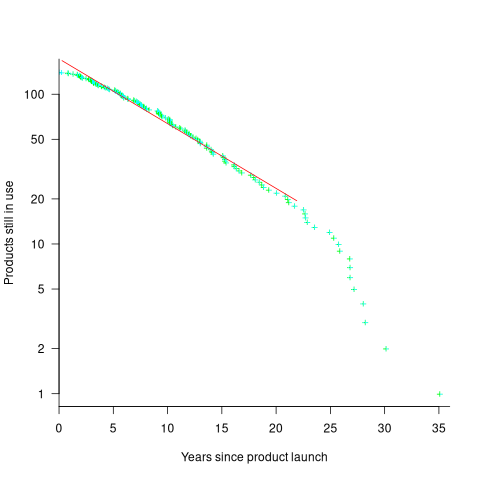
The half-life of the Microsoft products in this dataset, aged between 4 months and 22 years, is 7 years. Is the sharp decline in half-life after 22 years a real thing, or a consequence of the small amount of data before 2005? As always, more data is needed.
A distillation of Robert Glass’s lifetime experience
Robert Glass is a software engineering developer, manager, researcher and author who, until six months ago, I had vaguely heard of; somehow I had missed reading any of his 25 books. After seeing citations to some of Glass’s books, I bought half-a-dozen or so, second hand. They are well written, and twenty-five years ago I would have found them very interesting; now I simply agree with the points made.
“software creativity 2.0” is Glass’s penultimate book, published in 2006, and the one that caught my attention. I would recommend his other books to anybody who is new to software engineering, or experienced people looking for an encapsulation in print of what they encounter at work.
Glass was 74 when this book was published, having started working in computing in 1954. He was there and seems to have met many of the major names in software engineering, working with some of them.
The book is a clear-eyed summary of what Glass has learned from being involved with software engineering, and watching method/tool fashions come and go. My favourite section draws parallels between software development cultures and the culture of Rome vs. Greek vs. Barbarian:
Models Roman Greek Barbarians Organization Organize people Organize things Barely Focus Manages projects Writes programs Leap to coding Motivation Group goals Problem to be solved Heroics Working style Organizations Small groups Solo Politics Imperial Democratic Anarchist Tool use People are tools Things are tools Avoid tools Status Function-ocracy Meritocracy Fear-ocracy Activities Plan things Do things Break things Emphasize Form Substance Line of code |
The contents are essentially a collection of short essays, organized under the 19 chapter headings below, which in turn are grouped into four parts. The first nine chapters (part I, and 60% of pages) contain the experience based material, with the subsequent parts/pages having a creativity theme. A thread running through the discussion is idealism/practice:
Discipline vs. Flexibility
Formal methods versus Heuristics
Optimizing versus Satisficing
Quantitative versus Qualitative Reasoning
Process versus Product
Intellect vs. Clerical Tasks
Theory vs. Practice
Industry vs. Academe
Fun versus Getting Serious
Creativity in the Software Organization
Creativity in Software Technology
Creative Milestones in Software History
Organizational Creativity
The Creative Person
Computer Support for Creativity
Creativity Paradoxes#'twas Always Thus
A Synergistic Conclusion
Other Conclusions |
This book deserves to be widely read. I found it best to read a single section per sitting.
The lifetime of performance coding issues
Coding activities that a developer might spend time on include: adding new functionality, fixing a reported fault, or fiddling with existing code with the intent of making it ‘better’ in some sense (which these days goes by the catch-all name of refactoring).
Improving performance, e.g., changing software to use less cpu/memory is considered, by developers, to make it ‘better’ (whether users are likely to notice the difference, or management see a ROI is for another article). There is a breed of developer whose DNA encodes for pleasure receptors that are only fire when working to reduce the amount of cpu/memory used by a program.
The paper Characterizing the evolution of statically-detectable performance issues of Android Apps by Das, Di Penta, and Malavolta studied the creation/removal of nine distinct performance coding issues in the source of 316 Android Apps (118 Apps contained five or more issues); a total of 2,408 performance issues were tracked.
What patterns might be present in the paper’s performance issues data?
I would expect there to be more creations in Apps containing more code, and more removals the longer an App is maintained; both very obvious. With more developers working on an App, there are going to be more creations and removals; do they cancel out? Management might decide to invest time in performance improvements for the next release, which would cause a spike in the number of removals per unit time.
How long do the nine performance issues survive in code, before being removed? The plot below shows the Kaplan Meier survival curve for Apps containing at least five issues (dotted blue/green are the 95% confidence intervals, code+data):
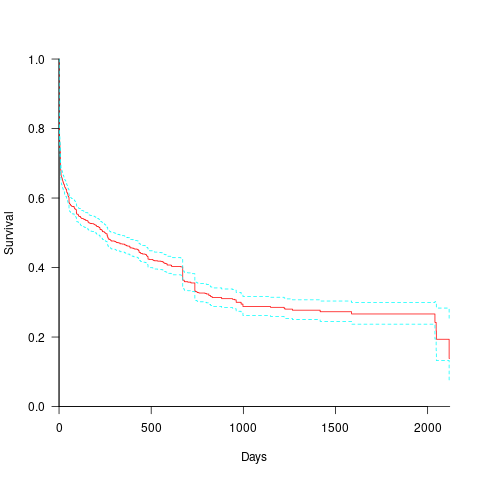
Around 15% of issues were removed on the day they are created, and by the eighth day around 30% had been removed. The roughly steady decline lasts for two-years, followed by almost stasis. Is two-years the active development lifetime of a successful Android App?
In isolation, the slope of the survival curve between eight days and two-years is not that interesting (it could be used to rule out models of the issue discovery process, e.g., happenstance discovery while working on other tasks). However, comparing it against the corresponding survival curve for reported faults tells us something about developer/management investment priorities for the two kinds of tasks, as measured by time to fix (which is a proxy for effort invested).
Unfortunately, this study did not collect information on coding mistake lifetimes, or time between a fault being reported and fixed. There have been studies investigating the survival time of coding mistakes. Reported faults should have the lowest survival rate, while the survival of coding mistakes will depend on the number of users (i.e., more users creates more opportunities to experience a fault and report it).
What factors influence performance issue time-to-fix?
The data includes information on the kind of performance issue, the number of times the App has been downloaded from the Google Play Store, and the number of contributors to the App.
Using these variables, a Cox proportional hazards model was fitted to model the survival time. In a proportional hazards model, the model coefficients are not absolute values, but provide ratio information. For instance, the following table shows the coefficients of the fitted model (code+data). Using these coefficients, we can compare the time taken to fix, say, a FloatMath issue relative to a ViewTag issue. The coefficient ratio 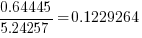 is the estimated ratio of fix times of the two respective issues.
is the estimated ratio of fix times of the two respective issues.
Coefficient Standard error Performance issue FloatMath 0.64445 0.14175 HandlerLeak 0.69958 0.12736 Recycle 0.83041 0.11386 UseSparseArrays 0.73471 0.12493 UseValueOf 0.64263 0.11827 ViewHolder 0.87253 0.14951 ViewTag 5.24257 0.46500 Wakelock 3.34665 0.72014 Downloads 50-100 0.62490 0.26245 100-500 0.64699 0.22494 500-1000 0.56768 0.23505 1000-5000 0.50707 0.22225 5000-10000 0.53432 0.22486 10000-50000 0.62449 0.21626 50000-100000 0.42214 0.23402 100000-500000 0.21479 0.25358 1000000-5000000 0.40593 0.21851 10000000-50000000 0.03474 0.61827 100000000-500000000 0.30693 0.39868 1000000000-5000000000 0.41522 0.61599 NA 0.03868 1.02076 Contributors 1.04996 0.01265 |
There is not a lot of difference in the coefficients for the number of downloads (the model fit is poor when the Standard error is close to the Coefficient value).
The paper Investigating Types and Survivability of Performance Bugs in Mobile Apps analyses a smaller dataset of performance issue lifetimes.
Cost-effectiveness decision for fixing a known coding mistake
If a mistake is spotted in the source code of a shipping software system, is it more cost-effective to fix the mistake, or to wait for a customer to report a fault whose root cause turns out to be that particular coding mistake?
The naive answer is don’t wait for a customer fault report, based on the following simplistic argument: 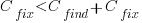 .
.
where: 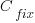 is the cost of fixing the mistake in the code (including testing etc), and
is the cost of fixing the mistake in the code (including testing etc), and 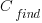 is the cost of finding the mistake in the code based on a customer fault report (i.e., the sum on the right is the total cost of fixing a fault reported by a customer).
is the cost of finding the mistake in the code based on a customer fault report (i.e., the sum on the right is the total cost of fixing a fault reported by a customer).
If the mistake is spotted in the code for ‘free’, then 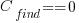 , e.g., a developer reading the code for another reason, or flagged by a static analysis tool.
, e.g., a developer reading the code for another reason, or flagged by a static analysis tool.
This answer is naive because it fails to take into account the possibility that the code containing the mistake is deleted/modified before any customers experience a fault caused by the mistake; let 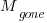 be the likelihood that the coding mistake ceases to exist in the next unit of time.
be the likelihood that the coding mistake ceases to exist in the next unit of time.
The more often the software is used, the more likely a fault experience based on the coding mistake occurs; let 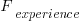 be the likelihood that a fault is reported in the next time unit.
be the likelihood that a fault is reported in the next time unit.
A more realistic analysis takes into account both the likelihood of the coding mistake disappearing and a corresponding fault being reported, modifying the relationship to: 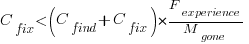
Software systems are eventually retired from service; the likelihood that the software is maintained during the next unit of time, 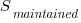 , is slightly less than one.
, is slightly less than one.
Giving the relationship: 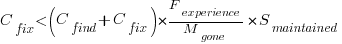
which simplifies to: 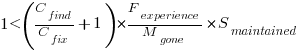
What is the likely range of values for the ratio: 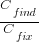 ?
?
I have no find/fix cost data, although detailed total time is available, i.e., find+fix time (with time probably being a good proxy for cost). My personal experience of find often taking a lot longer than fix probably suffers from survival of memorable cases; I can think of cases where the opposite was true.
The two values in the ratio 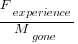 are likely to change as a system evolves, e.g., high code turnover during early releases that slows as the system matures. The value of
are likely to change as a system evolves, e.g., high code turnover during early releases that slows as the system matures. The value of 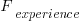 should decrease over time, but increase with a large influx of new users.
should decrease over time, but increase with a large influx of new users.
A study by Penta, Cerulo and Aversano investigated the lifetime of coding mistakes (detected by several tools), tracking them over three years from creation to possible removal (either fixed because of a fault report, or simply a change to the code).
Of the 2,388 coding mistakes detected in code developed over 3-years, 41 were removed as reported faults and 416 disappeared through changes to the code: 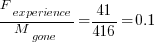
The plot below shows the survival curve for memory related coding mistakes detected in Samba, based on reported faults (red) and all other changes to the code (blue/green, code+data):
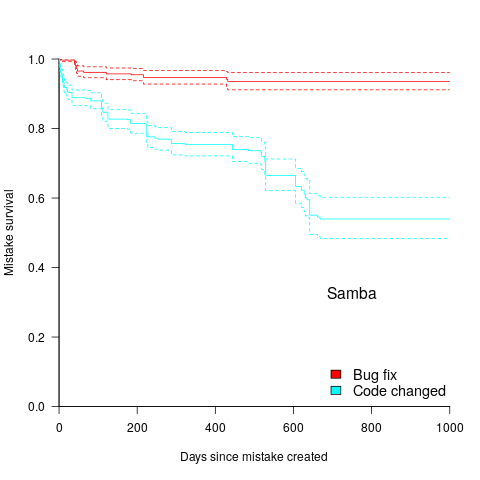
Coding mistakes are obviously being removed much more rapidly due to changes to the source, compared to customer fault reports.
For it to be cost-effective to fix coding mistakes in Samba, flagged by the tools used in this study (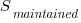 is essentially one), requires:
is essentially one), requires: 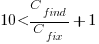 .
.
Meeting this requirement does not look that implausible to me, but obviously data is needed.
Many coding mistakes are not immediately detectable
Earlier this week I was reading a paper discussing one aspect of the legal fallout around the UK Post-Office’s Horizon IT system, and was surprised to read the view that the Law Commission’s Evidence in Criminal Proceedings Hearsay and Related Topics were citing on the subject of computer evidence (page 204): “most computer error is either immediately detectable or results from error in the data entered into the machine”.
What? Do I need to waste any time explaining why this is nonsense? It’s obvious nonsense to anybody working in software development, but this view is being expressed in law related documents; what do lawyers know about software development.
Sometimes fallacies become accepted as fact, and a lot of effort is required to expunge them from cultural folklore. Regular readers of this blog will have seen some of my posts on long-standing fallacies in software engineering. It’s worth collecting together some primary evidence that most software mistakes are not immediately detectable.
A paper by Professor Tapper of Oxford University is cited as the source (yes, Oxford, home of mathematical orgasms in software engineering). Tapper’s job title is Reader in Law, and on page 248 he does say: “This seems quite extraordinarily lax, given that most computer error is either immediately detectable or results from error in the data entered into the machine.” So this is not a case of his words being misinterpreted or taken out of context.
Detecting many computer errors is resource intensive, both in elapsed time, manpower and compute time. The following general summary provides some of the evidence for this assertion.
Two events need to occur for a fault experience to occur when running software:
- a mistake has been made when writing the source code. Mistakes include: a misunderstanding of what the behavior should be, using an algorithm that does not have the desired behavior, or a typo,
- the program processes input values that interact with a coding mistake in a way that produces a fault experience.
That people can make different mistakes is general knowledge. It is my experience that people underestimate the variability of the range of values that are presented as inputs to a program.
A study by Nagel and Skrivan shows how variability of input values results in fault being experienced at different time, and that different people make different coding mistakes. The study had three experienced developers independently implement the same specification. Each of these three implementations was then tested, multiple times. The iteration sequence was: 1) run program until fault experienced, 2) fix fault, 3) if less than five faults experienced, goto step (1). This process was repeated 50 times, always starting with the original (uncorrected) implementation; the replications varied this, along with the number of inputs used.
How many input values needed to be processed, on average, before a particular fault is experienced? The plot below (code+data) shows the numbers of inputs processed, by one of the implementations, before individual faults were experienced, over 50 runs (sorted by number of inputs needed before the fault was experienced):
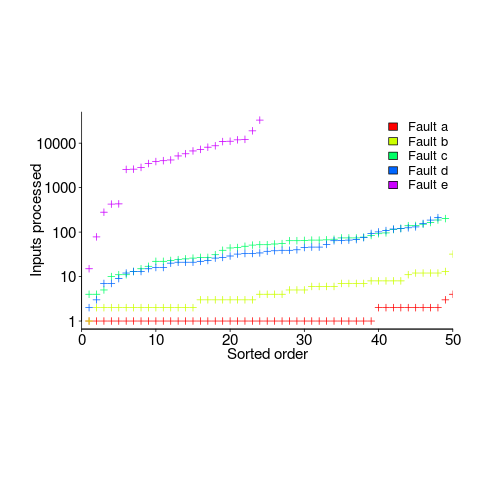
The plot illustrates that some coding mistakes are more likely to produce a fault experience than others (because they are more likely to interact with input values in a way that generates a fault experience), and it also shows how the number of inputs values processed before a particular fault is experienced varies between coding mistakes.
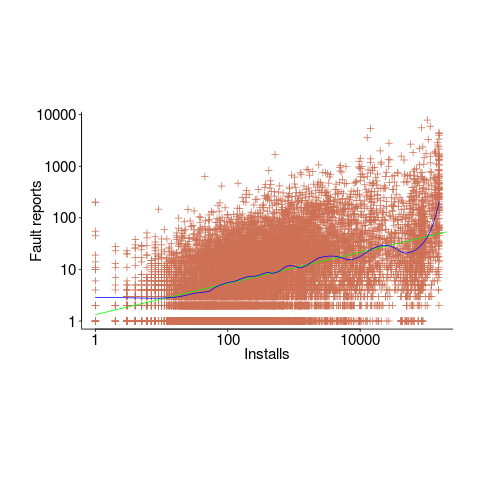
Real-world evidence of the impact of user input on reported faults is provided by the Ultimate Debian Database, which provides information on the number of reported faults and the number of installs for 14,565 packages. The plot below shows how the number of reported faults increases with the number of times a package has been installed; one interpretation is that with more installs there is a wider variety of input values (increasing the likelihood of a fault experience), another is that with more installs there is a larger pool of people available to report a fault experience. Green line is a fitted power law, 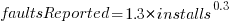 , blue line is a fitted loess model.
, blue line is a fitted loess model.
The source containing a mistake may be executed without a fault being experienced; reasons for this include:
- the input values don’t result in the incorrect code behaving differently from the correct code. For instance, given the made-up incorrect code
if (x < 8)(i.e.,8was typed rather than7), the comparison only produces behavior that differs from the correct code whenxhas the value7, - the input values result in the incorrect code behaving differently than the correct code, but the subsequent path through the code produces the intended external behavior.
Some of the studies that have investigated the program behavior after a mistake has deliberately been introduced include:
- checking the later behavior of a program after modifying the value of a variable in various parts of the source; the results found that some parts of a program were more susceptible to behavioral modification (i.e., runtime behavior changed) than others (i.e., runtime behavior not change),
- checking whether a program compiles and if its runtime behavior is unchanged after random changes to its source code (in this study, short programs written in 10 different languages were used),
- 80% of radiation induced bit-flips have been found to have no externally detectable effect on program behavior.
What are the economic costs and benefits of finding and fixing coding mistakes before shipping vs. waiting to fix just those faults reported by customers?
Checking that a software system exhibits the intended behavior takes time and money, and the organization involved may not be receiving any benefit from its investment until the system starts being used.
In some applications the cost of a fault experience is very high (e.g., lowering the landing gear on a commercial aircraft), and it is cost-effective to make a large investment in gaining a high degree of confidence that the software behaves as expected.
In a changing commercial world software systems can become out of date, or superseded by new products. Given the lifetime of a typical system, it is often cost-effective to ship a system expected to contain many coding mistakes, provided the mistakes are unlikely to be executed by typical customer input in a way that produces a fault experience.
Beta testing provides selected customers with an early version of a new release. The benefit to the software vendor is targeted information about remaining coding mistakes that need to be fixed to reduce customer fault experiences, and the benefit to the customer is checking compatibility of their existing work practices with the new release (also, some people enjoy being able to brag about being a beta tester).
- One study found that source containing a coding mistake was less likely to be changed due to fixing the mistake than changed for other reasons (that had the effect of causing the mistake to disappear),
- Software systems don't live forever; systems are replaced or cease being used. The plot below shows the lifetime of 202 Google applications (half-life 2.9 years) and 95 Japanese mainframe applications from the 1990s (half-life 5 years; code+data).
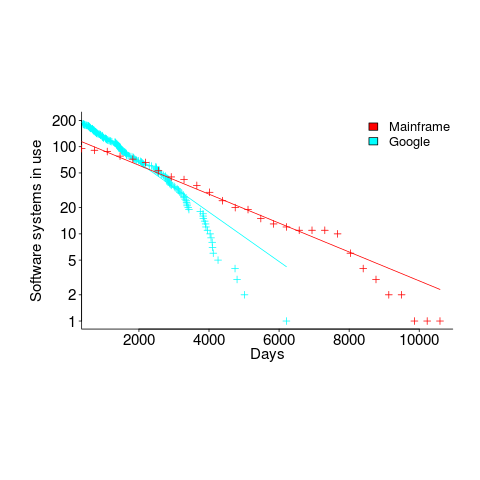
Not only are most coding mistakes not immediately detectable, there may be sound economic reasons for not investing in detecting many of them.
Learning useful stuff from the Ecosystems chapter of my book
What useful, practical things might professional software developers learn from the Ecosystems chapter in my evidence-based software engineering book?
This week I checked the ecosystems chapter; what useful things did I learn (combined with everything I learned during all the other weeks spent working on this chapter)?
A casual reader would conclude that software engineering ecosystems involved lots of topics, with little or no theory connecting them. I had great plans for the connecting theories, but lack of detailed data, time and inspiration means the plans remain in my head (e.g., modelling the interaction between the growth of source code written in a particular language and the number of developers actively using that language).
For managers, the usefulness of this chapter is the strategic perspective it provides. How does what they and others are doing relate to everything else, and what patterns of evolution are to be expected?
Software people like to think that everything about software is unique. Software is unique, but the activities around it follow patterns that have been followed by other unique technologies, e.g., the automobile and jet engines. There is useful stuff to be learned from non-software ecosystems, and the chapter discusses some similarities I have learned about.
There is lots more evidence of the finite lifetime of software related items: lifetime of products, Linux distributions, packages, APIs and software careers.
Some readers might be surprised by the amount of discussion about what is now historical hardware. Software needs hardware to execute it, and the characteristics of the hardware of the day can have a significant impact on the characteristics of the software that gets written. I suspect that most of this discussion will not be that useful to most readers, but it provides some context around why things are the way they are today.
Readers with a wide knowledge of software ecosystems will notice that several major ecosystems barely get a mention. Embedded systems is a huge market, as is Microsoft Windows, and very many professional developers use C++. However, to date the focus of most research has been around Linux and Android (because its use of Java, a language often taught in academia), and languages that have a major package repository. So the ecosystems chapter presents a rather blinkered view of software engineering ecosystems.
What did I learn from this chapter?
Software ecosystems are bigger and more complicated that I had originally thought.
Readers might have a completely different learning experience from reading the ecosystems chapter. What useful things did you learn from the ecosystems chapter?
Learning useful stuff from the Projects chapter of my book
What useful, practical things might professional software developers learn from the Projects chapter in my evidence-based software engineering book?
This week I checked the projects chapter; what useful things did I learn (combined with everything I learned during all the other weeks spent working on this chapter)?
There turned out to be around three to four times more data publicly available than I had first thought. This is good, but there is a trap for the unweary. For many topics there is one data set, and that one data set may not be representative. What is needed is a selection of data from various sources, all relating to a given topic.
Some data is better than no data, provided small data sets are treated with caution.
Estimation is a popular research topic: how long will a project take and how much will it cost.
After reading all the papers I learned that existing estimation models are even more unreliable than I had thought, and what is more, there are plenty of published benchmarks showing how unreliable the models really are (these papers never seem to get cited).
Models that include lines of code in the estimation process (i.e., the majority of models) need a good estimate of the likely number of lines in the final software system. One issue that nobody had considered was the impact of developer variability on the number of lines written to implement the same functionality, which turns out to be large. Oops.
Machine learning has infested effort estimation research. What the machine learning models actually do is estimate adjustment, i.e., they do not create their own estimate but adjust one passed in as input to the model. Most estimation data sets are tiny, and only contain a few different variables; unless the estimate is included in the training phase, the generated model produces laughable results. Oops.
The good news is that there appear to be lots of recurring patterns in the project data. This is good news because recurring patterns are something to be explained by a theory of software project development (apparent randomness is bad news, from the perspective of coming up with a model of what is going on). I think we are still a long way from having workable theories, but seeing patterns is a good sign that one or more theories will be possible.
I think that the main takeaway from this chapter is that software often has a short lifetime. People in industry probably have a vague feeling that this is true, from experience with short-lived projects. It is not cost effective to approach commercial software development from the perspective that the code will live a long time; some code does live a long time, but most dies young. I see the implications of this reality being a major source of contention with those in academia who have spent too long babbling away in front of teenagers (teaching the creation of idealized software that lives on forever), and little or no time building software systems.
A lot of software is written by teams of people, however, there is not a lot of data available on teams (software or otherwise). Given the difficulty of hiring developers, companies have to make do with what they have, so a theory of software teams might not be that useful in practice.
Readers might have a completely different learning experience from reading the projects chapter. What useful things did you learn from the projects chapter?
Source code has a brief and lonely existence
The majority of source code has a short lifespan (i.e., a few years), and is only ever modified by one person (i.e., 60%).
Literate programming is all well and good for code written to appear in a book that the author hopes will be read for many years, but this is a tiny sliver of the source code ecosystem. The majority of code is never modified, once written, and does not hang around for very long; an investment is source code futures will make a loss unless the returns are spectacular.
What evidence do I have for these claims?
There is lots of evidence for the code having a short lifespan, and not so much for the number of people modifying it (and none for the number of people reading it).
The lifespan evidence is derived from data in my evidence-based software engineering book, and blog posts on software system lifespans, and survival times of Linux distributions. Lifespan in short because Packages are updated, and third-parties change/delete APIs (things may settle down in the future).
People who think source code has a long lifespan are suffering from survivorship bias, i.e., there are a small percentage of programs that are actively used for many years.
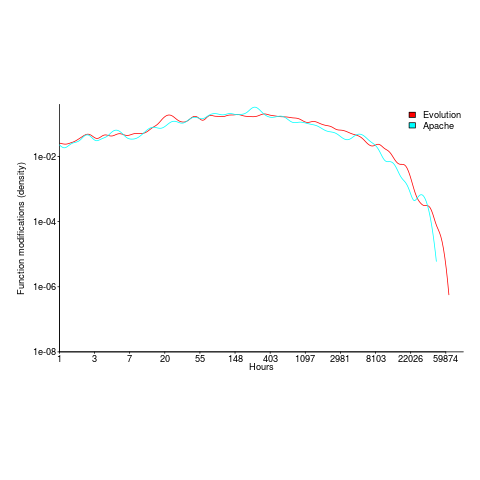
Around 60% of functions are only ever modified by one author; based on a study of the change history of functions in Evolution (114,485 changes to functions over 10 years), and Apache (14,072 changes over 12 years); a study investigating the number of people modifying files in Eclipse. Pointers to other studies that have welcome.
One consequence of the short life expectancy of source code is that, any investment made with the expectation of saving on future maintenance costs needs to return many multiples of the original investment. When many programs don’t live long enough to be maintained, those with a long lifespan have to pay the original investments made in all the source that quickly disappeared.
One benefit of short life expectancy is that most coding mistakes don’t live long enough to trigger a fault experience; the code containing the mistake is deleted or replaced before anybody notices the mistake.
Update: a few days later
I was remiss in not posting some plots for people to look at (code+data).
The plot below shows number of function, in Evolution, modified a given number of times (left), and functions modified by a given number of authors (right). The lines are a bi-exponential fit.

What is the interval (in hours) between between modifications of a function? The plot below has a logarithmic x-axis, and is sort-of flat over most of the range (you need to squint a bit). This is roughly saying that the probability of modification in hours 1-3 is the same as in hours 3-7, and hours, 7-15, etc (i.e., keep doubling the hour interval). At round 10,000 hours function modification probability drops like a stone.
Half-life of software as a service, services
How is software used to provide a service (e.g., the software behind gmail) different from software used to create a product (e.g., sold as something that can be installed)?
This post focuses on one aspect of the question, software lifetime.
The Killed by Google website lists Google services and products that are no more. Cody Ogden, the creator of the site, has open sourced the code of the website; there are product start/end dates!
After removing 20 hardware products from the list, we are left with 134 software services. Some of the software behind these services came from companies acquired by Google, so the software may have been used to provide a service pre-acquisition, i.e., some calculated lifetimes are underestimates.
The plot below shows the number of Google software services (blue) having a given lifetime (calculated as days between Google starting/withdrawing service), mainframe software from the 1990s (red; only available at yearly resolution), along with fitted exponential regression lines (code+data):

Overall, an exponential is a good fit (squinting to ignore the dozen red points), although product culling is not exponentially ruthless at short lifetimes (newly launched products are given a chance to prove themselves).
The Google service software half-life is 1,500 days, about 4.1 years (assuming the error/uncertainty is additive, if it is multiplicative {i.e., a percentage} the half-life is 1,300 days); the half-life of mainframe software is 2,600 days (with the same assumption about the kind of error/uncertainty).
One explanation of the difference is market maturity. Mainframe software has been evolving since the 1950s and probably turned over at the kind of rate we saw a few years ago with Internet services. By the 1990s things had settled down a bit in the mainframe world. Will software-based services on the Internet settle down faster than mainframe software? Who knows.
Based on this Google data, the cost/benefit ratio when deciding whether to invest in reducing future software maintenance costs, is going to have to be significantly better than the ratio calculated for mainframe software.
Software system lifetime data is extremely hard to find (this is only the second set I have found). Any pointers to other lifetime data very welcome, e.g., a collection of Microsoft product start/end dates
Break even ratios for development investment decisions
Developers are constantly being told that it is worth making the effort when writing code to make it maintainable (whatever that might be). Looking at this effort as an investment what kind of return has to be achieved to make it worthwhile?
Short answer: The percentage saving during maintenance has to be twice as great as the percentage investment during development to break even, higher ratio to do better.
The longer answer is below as another draft section from my book Empirical software engineering with R book. As always comments and pointers to more data welcome. R code and data here.
Break even ratios for development investment decisions
Upfront investments are often made during software development with the aim of achieving benefits later (e.g., reduced cost or time). Examples of such investments include spending time planning, designing or commenting the code. The following analysis calculates the benefit that must be achieved by an investment for that investment to break even.
While the analysis uses years as the unit of time it is not unit specific and with suitable scaling months, weeks, hours, etc can be used. Also the unit of development is taken to be a complete software system, but could equally well be a subsystem or even a function written by one person.
Let 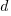 be the original development cost and
be the original development cost and 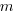 the yearly maintenance costs, we start by keeping things simple and assume
the yearly maintenance costs, we start by keeping things simple and assume 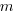 is the same for every year of maintenance; the total cost of the system over
is the same for every year of maintenance; the total cost of the system over 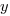 years is:
years is:
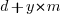
If we make an investment of 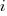 % in reducing future maintenance costs with the expectations of achieving a benefit of
% in reducing future maintenance costs with the expectations of achieving a benefit of 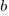 %, the total cost becomes:
%, the total cost becomes:
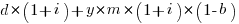
and for the investment to break even the following inequality must hold:
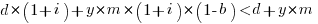
expanding and simplifying we get:
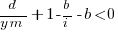
or:
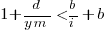
If the inequality is true the ratio 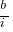 is the primary contributor to the right-hand-side and must be greater than 1.
is the primary contributor to the right-hand-side and must be greater than 1.
A significant problem with the above analysis is that it does not take into account a major cost factor; many systems are replaced after a surprisingly short period of time. What relationship does the 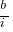 ratio need to have when system survival rate is taken into account?
ratio need to have when system survival rate is taken into account?
Let 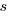 be the percentage of systems that survive each year, total system cost is now:
be the percentage of systems that survive each year, total system cost is now:
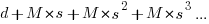
where 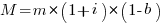
Summing the power series for the maximum of 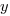 years that any system in a company’s software portfolio survives gives:
years that any system in a company’s software portfolio survives gives:
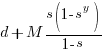
and the break even inequality becomes:
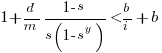
The development/maintenance ratio is now based on the yearly cost multiplied by a factor that depends on the system survival rate, not the total maintenance cost
If we take 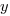 >= 5 and a survival rate of less than 60% the inequality simplifies to very close to:
>= 5 and a survival rate of less than 60% the inequality simplifies to very close to:
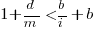
telling us that if the yearly maintenance cost is equal to the development cost (a situation more akin to continuous development than maintenance and seen in 5% of systems in the IBM dataset below) then savings need to be at least twice as great as the investment for that investment to break even. Taking the mean of the IBM dataset and assuming maintenance costs spread equally over the 5 years, a break even investment requires savings to be six times greater than the investment (for a 60% survival rate).
The plot below gives the minimum required saving/investment ratio that must be achieved for various system survival rates (black 0.9, red 0.8, blue 0.7 and green 0.6) and development/yearly maintenance cost ratios; the line bundles are for system lifetimes of 5.5, 6, 6.5, 7 and 7.5 years (ordered top to bottom)

Figure 1. Break even saving/investment ratio for various system survival rates (black 0.9, red 0.8, blue 0.7 and green 0.6) and development/maintenance ratios; system lifetimes are 5.5, 6, 6.5, 7 and 7.5 years (ordered top to bottom)
Development and maintenance costs
Dunn’s PhD thesis <book Dunn_11> lists development and total maintenance costs (for the first five years) of 158 software systems from IBM. The systems varied in size from 34 to 44,070 man hours of development effort and from 21 to 78,121 man hours of maintenance.
The plot below shows the ratio of development to five year maintenance costs for the 158 software systems. The mean value is around one and if we assume equal spending during the maintenance period then 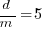 .
.
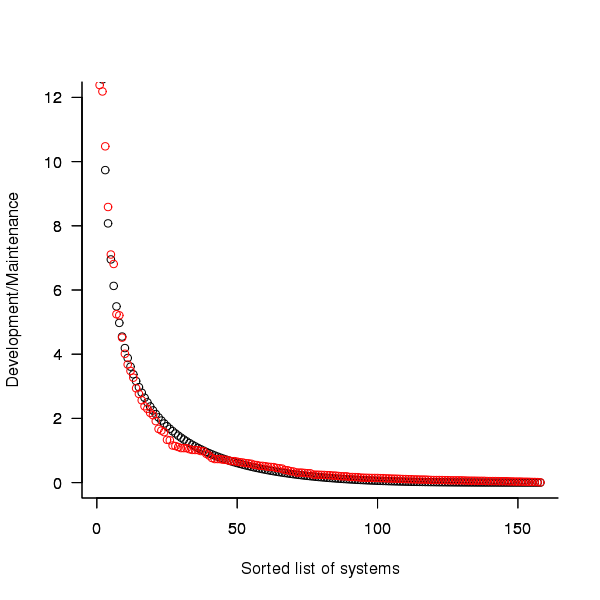
Figure 2. Ratio of development to five year maintenance costs for 158 IBM software systems sorted in size order. Data from Dunn <book Dunn_11>.
The best fitting common distribution for the maintenance/development ratio is the <Beta distribution>, a distribution often encountered in project planning.
Is there a correlation between development man hours and the maintenance/development ratio (e.g., do smaller systems tend to have a lower/higher ratio)? A Spearman rank correlation test between the maintenance/development ratio and development man hours gives:
|
showing very little connection between the two values.
Is the data believable?
While a single company dataset might be thought to be internally consistent in its measurement process, IBM is a very large company and it is possible that the measurement processes used were different.
The maintenance data applies to software systems that have not yet reached the end of their lifespan and is not broken down by year. Any estimate of total or yearly maintenance can only be based on assumptions or lifespan data from other studies.
System lifetime
A study by Tamai and Torimitsu <book Tamai_92> obtained data on the lifespan of 95 software systems. The plot below shows the number of systems surviving for at least a given number of years and a fit of an <Exponential distribution> to the data.
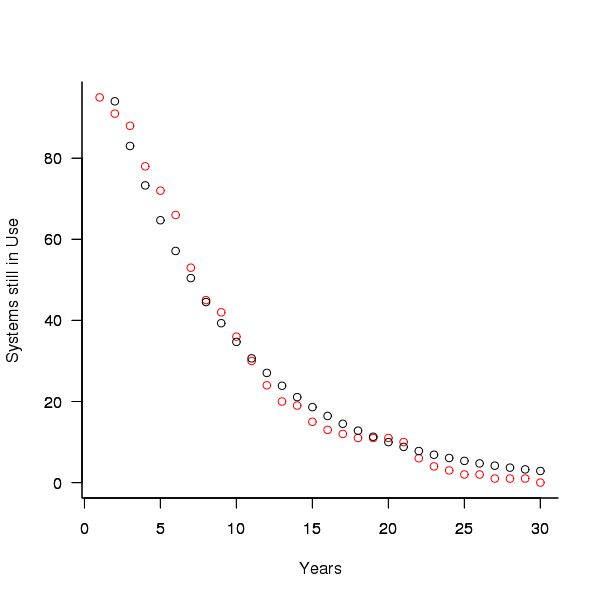
Figure 3. Number of software systems surviving to a given number of years (red) and an exponential fit (black, data from Tamai <book Tamai_92>).
The nls function gives 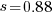 as the best fit, giving a half-life of 5.4 years (time for the number of systems to reduce by 50%), while rounding to
as the best fit, giving a half-life of 5.4 years (time for the number of systems to reduce by 50%), while rounding to 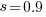 gives a half-life of 6.6 years and reducing to
gives a half-life of 6.6 years and reducing to 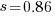 a half life of 4.6 years.
a half life of 4.6 years.
It is worrying that such a small change to the estimated fit can have such a dramatic impact on estimated half-life, especially given the uncertainty in the applicability of the 20 year old data to today’s environment. However, the saving/investment ratio plot above shows that the final calculated value is not overly sensitive to number of years.
Is the data believable?
The data came from a questionnaire sent to the information systems division of corporations using mainframes in Japan during 1991.
It could be argued that things have stabilised over the last 20 years ago and complete software replacements are rare with most being updated over longer periods, or that growing customer demands is driving more frequent complete system replacement.
It could be argued that large companies have larger budgets than smaller companies and so have the ability to change more quickly, or that larger companies are intrinsically slower to change than smaller companies.
Given the age of the data and the application environment it came from a reasonably wide margin of uncertainty must be assigned to any usage patterns extracted.
Summary
Based on the available data an investment during development must recoup a benefit during maintenance that is at least twice as great in percentage terms to break even:
- systems with a yearly survival rate of less than 90% must have a benefit/investment rate greater than two if they are to break even,
- systems with a development/yearly maintenance rate of greater than 20% must have a benefit/investment rate greater than two if they are to break even.
The availanble software system replacement data is not reliable enough to suggest any more than that the estimated half-life might be between 4 and 8 years.
This analysis only considers systems that have been delivered and started to be used. Projects are cancelled before reaching this stage and including these in the analysis would increase the benefit/investment break even ratio.

Recent Comments