Archive
Estimating quantities from several hundred to several thousand
How much influence do anchoring and financial incentives have on estimation accuracy?
Anchoring is a cognitive bias which occurs when a decision is influenced by irrelevant information. For instance, a study by John Horton asked 196 subjects to estimate the number of dots in a displayed image, but before providing their estimate subjects had to specify whether they thought the number of dots was higher/lower than a number also displayed on-screen (this was randomly generated for each subject).
How many dots do you estimate appear in the plot below?

Estimates are often round numbers, and 46% of dot estimates had the form of a round number. The plot below shows the anchor value seen by each subject and their corresponding estimate of the number of dots (the image always contained five hundred dots, like the one above), with round number estimates in same color rows (e.g., 250, 300, 500, 600; code+data):
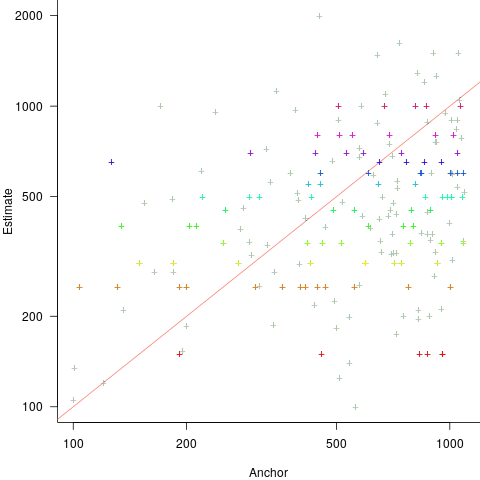
How much influence does the anchor value have on the estimated number of dots?
One way of measuring the anchor’s influence is to model the estimate based on the anchor value. The fitted regression equation 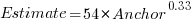 explains 11% of the variance in the data. If the higher/lower choice is included the model, 44% of the variance is explained; higher equation is:
explains 11% of the variance in the data. If the higher/lower choice is included the model, 44% of the variance is explained; higher equation is: 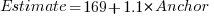 and lower equation is:
and lower equation is: 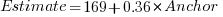 (a multiplicative model has a similar goodness of fit), i.e., the anchor has three-times the impact when it is thought to be an underestimate.
(a multiplicative model has a similar goodness of fit), i.e., the anchor has three-times the impact when it is thought to be an underestimate.
How much would estimation accuracy improve if subjects’ were given the option of being rewarded for more accurate answers, and no anchor is present?
A second experiment offered subjects the choice of either an unconditional payment of $2.50 or a payment of $5.00 if their answer was in the top 50% of estimates made (labelled as the risk condition).
The 196 subjects saw up to seven images (65 only saw one), with the number of dots varying from 310 to 8,200. The plot below shows actual number of dots against estimated dots, for all subjects; blue/green line shows 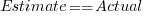 , and red line shows the fitted regression model
, and red line shows the fitted regression model 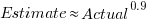 (code+data):
(code+data):
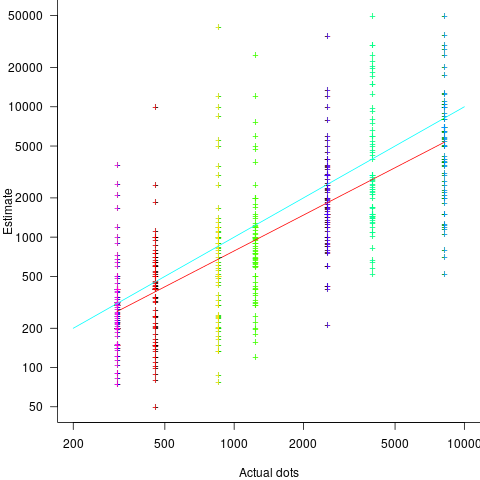
The variance in the estimated number of dots is very high and increases with increasing actual dot count, however, this behavior is consistent with the increasing variance seen for images containing under 100 dots.
Estimates were not more accurate in those cases where subjects chose the risk payment option. This is not surprising, performance improvements require feedback, and subjects were not given any feedback on the accuracy of their estimates.
Of the 86 subjects estimating dots in three or more images, 44% always estimated low and 16% always high. Subjects always estimating low/high also occurs in software task estimates.
Estimation patterns previously discussed on this blog have involved estimated values below 100. This post has investigated patterns in estimates ranging from several hundred to several thousand. Patterns seen include extensive use of round numbers and increasing estimate variance with increasing actual value; all seen in previous posts.
Most percentages are more than half
Most developers think …
Most editors …
Most programs …
Linguistically most is a quantifier (it’s a proportional quantifier); a word-phrase used to convey information about the number of something, e.g., all, any, lots of, more than half, most, some.
Studies of most have often compared and contrasted it with the phrase more than half; findings include: most has an upper bound (i.e., not all), and more than half has a lower bound (but no upper bound).
A corpus analysis of most (432,830 occurrences) and more than half (4,857 occurrences) found noticeable usage differences. Perhaps the study’s most interesting finding, from a software engineering perspective, was that most tended to be applied to vague and uncountable domains (i.e., there was no expectation that the population of items could be counted), while uses of more than half almost always had a ‘survey results’ interpretation (e.g., supporting data cited as collaboration for 80% of occurrences; uses of most cited data for 19% of occurrences).
Readers will be familiar with software related claims containing the most qualifier, which are actually opinions that are not grounded in substantive numeric data.
When most is used in a numeric based context, what percentage (of a population) is considered to be most (of the population)?
When deciding how to describe a proportion, a writer has the choice of using more than half, most, or another qualifier. Corpus based studies find that the distribution of most has a higher average percentage value than more than half (both are left skewed, with most peaking around 80-85%).
When asked to decide whether a phrase using a qualifier is true/false, with respect to background information (e.g., Given that 55% of the birlers are enciad, is it true that: Most of the birlers are enciad?), do people treat most and more than half as being equivalent?
A study by Denić and Szymanik addressed this question. Subjects (200 took part, with results from 30 were excluded for various reasons) saw a statement involving a made-up object and verb, such as: “55% of the birlers are enciad.” They then saw a sentence containing either most or more than half, that was either upward-entailing (e.g., “More than half of the birlers are enciad.”), or downward-entailing (e.g., “It is not the case that more than half of the birlers are enciad.”); most/more than half and upward/downward entailing creates four possible kinds of sentence. Subjects were asked to respond true/false.
The percentage appearing in the first sentence of the two seen by subjects varied, e.g., “44% of the tiklets are hullaw.”, “12% of the puggles are entand.”, “68% of the plipers are sesare.” The percentage boundary where each subjects’ true/false answer switched was calculated (i.e., the mean of the percentages present in the questions’ each side of true/false boundary; often these values were 46% and 52%, whose average is 49; this is an artefact of the question wording).
The plot below shows the number of subjects whose true/false boundary occurred at a given percentage (code+data):
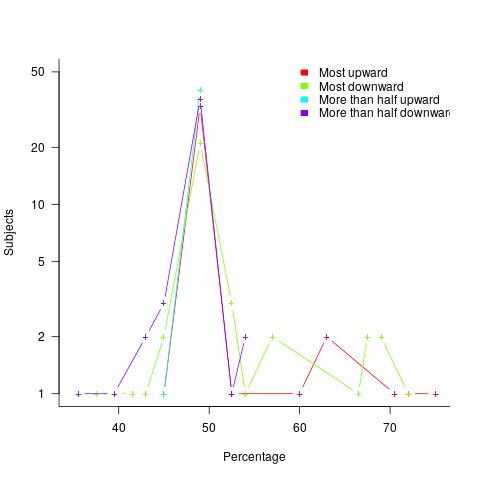
When asked, the majority of subjects had a 50% boundary for most/more than half+upward/downward. A downward entailment causes some subjects to lower their 50% boundary.
So now we know (subject to replication). Most people are likely to agree that 50% is the boundary for most/more than half, but some people think that the boundary percentage is higher for most.
When asked to write a sentence, percentages above 50% attract more mosts than more than halfs.
Most is preferred when discussing vague and uncountable domains; more than half is used when data is involved.
Study of developers for the cost of a phase I clinical drug trial
For many years now, I have been telling people that software researchers need to be more ambitious and apply for multi-million pound/dollar grants to run experiments in software engineering. After all, NASA spends a billion or so sending a probe to take some snaps of a planet and astronomers lobby for $100million funding for a new telescope.
What kind of experimental study might be run for a few million pounds (e.g., the cost of a Phase I clinical drug trial)?
Let’s say that each experiment involves a team of professional developers implementing a software system; call this a Project. We want the Project to be long enough to be realistic, say a week.
Different people exhibit different performance characteristics, and the experimental technique used to handle this is to have multiple teams independently implement the same software system. How many teams are needed? Fifteen ought to be enough, but more is better.
Different software systems contain different components that make implementation easier/harder for those involved. To remove single system bias, a variety of software systems need to be used as Projects. Fifteen distinct Projects would be great, but perhaps we can get away with five.
How many developers are on a team? Agile task estimation data shows that most teams are small, i.e., mostly single person, with two and three people teams making up almost all the rest.
If we have five teams of one person, five of two people, and five of three people, then there are 15 teams and 30 people.
How many people will be needed over all Projects?
15 teams (30 people) each implementing one Project 5 Projects, which will require 5*30=150 people (5*15=75 teams) |
How many person days are likely to be needed?
If a 3-person team takes a week (5 days), a 2-person team will take perhaps 7-8 days. A 1-person team might take 9-10 days.
The 15 teams will consume 5*3*5+5*2*7+5*1*9=190 person days The 5 Projects will consume 5*190=950 person days |
How much is this likely to cost?
The current average daily rate for a contractor in the UK is around £500, giving an expected cost of 190*500=£475,000 to hire the experimental subjects. Venue hire is around £40K (we want members of each team to be co-located).
The above analysis involves subjects implementing one Project. If, say, each subject implements two, three or four Projects, one after the other, the cost is around £2million, i.e., the cost of a Phase I clinical drug trial.
What might we learn from having subjects implement multiple Projects?
Team performance depends on the knowledge and skill of its members, and their ability to work together. Data from these experiments would be the first of their kind, and would provide realistic guidance on performance factors such as: impact of team size; impact of practice; impact of prior experience working together; impact of existing Project experience. The multiple implementations of the same Project created provide a foundation for measuring expected reliability and theories of N-version programming.
A team of 1 developer will take longer to implement a Project than a team of 2, who will take longer than a team of 3.
If 20 working days is taken as the ballpark period over which a group of subjects are hired (i.e., a month), there are six team size sequences that one subject could work (A to F below); where individual elapsed time is close to 20 days (team size 1 is 10 days elapsed, team size 2 is 7.5 days, team size 3 is 5 days).
Team size A B C D E F
1 twice once once
2 once thrice once
3 twice twice four |
The cost of hiring subjects+venue+equipment+support for such a study is likely to be at least £1,900,000.
If the cost of beta testing, venue hire and research assistants (needed during experimental runs) is included, the cost is close to £2.75 million.
Might it be cheaper and simpler to hire, say, 20-30 staff from a medium size development company? I chose a medium-sized company because we would be able to exert some influence over developer selection and keeping the same developers involved. The profit from 20-30 people for a month is not enough to create much influence within a large company, and a small company would not want to dedicate a large percentage of its staff for a solid month.
Beta testing is needed to validate both the specifications for each Project and that it is possible to schedule individuals to work in a sequence of teams over a month (individual variations in performance create a scheduling nightmare).
Estimation experiments: specification wording is mostly irrelevant
Existing software effort estimation datasets provide information about estimates made within particular development environments and with particular aims. Experiments provide a mechanism for obtaining information about estimates made under conditions of the experimenters choice, at least in theory.
Writing the code is sometimes the least time-consuming part of implementing a requirement. At hackathons, my default estimate for almost any non-trivial requirement is a couple of hours, because my implementation strategy is to find the relevant library or package and write some glue code around it. In a heavily bureaucratic organization, the coding time might be a rounding error in the time taken up by meeting, documentation and testing; so a couple of months would be considered normal.
If we concentrate on the time taken to implement the requirements in code, then estimation time and implementation time will depend on prior experience. I know that I can implement a lexer for a programming language in half-a-day, because I have done it so many times before; other people take a lot longer because they have not had the amount of practice I have had on this one task. I’m sure there are lots of tasks that would take me many days, but there is somebody who can implement them in half-a-day (because they have had lots of practice).
Given the possibility of a large variation in actual implementation times, large variations in estimates should not be surprising. Does the possibility of large variability in subject responses mean that estimation experiments have little value?
I think that estimation experiments can provide interesting information, as long as we drop the pretence that the answers given by subjects have any causal connection to the wording that appears in the task specifications they are asked to estimate.
If we assume that none of the subjects is sufficiently expert in any of the experimental tasks specified to realistically give a plausible answer, then answers must be driven by non-specification issues, e.g., the answer the client wants to hear, a value that is defensible, a round number.
A study by Lucas Gren and Richard Berntsson Svensson asked subjects to estimate the total implementation time of a list of tasks. I usually ignore software engineering experiments that use student subjects (this study eventually included professional developers), but treating the experiment as one involving social processes, rather than technical software know-how, makes subject software experience a lot less relevant.
Assume, dear reader, that you took part in this experiment, saw a list of requirements that sounded plausible, and were then asked to estimate implementation time in weeks. What estimate would you give? I would have thrown my hands up in frustration and might have answered 0.1 weeks (i.e., a few hours). I expected the most common answer to be 4 weeks (the number of weeks in a month), but it turned out to be 5 (a very ‘attractive’ round number), for student subjects (code+data).
The professional subjects appeared to be from large organizations, who I assume are used to implementations including plenty of bureaucratic stuff, as well as coding. The task specification did not include enough detailed information to create an accurate estimate, so subjects either assumed their own work environment or played along with the fresh-faced, keen experimenter (sorry Lucas). The professionals showed greater agreement in that the range of value given was not as wide as students, but it had a more uniform distribution (with maximums, rather than peaks, at 4 and 7); see below. I suspect that answers at the high end were from managers and designers with minimal coding experience.
What did the experimenters choose weeks as the unit of estimation? Perhaps they thought this expressed a reasonable implementation time (it probably is if it’s not possible to use somebody else’s library/package). I think that they could have chosen day units and gotten essentially the same results (at least for student subjects). If they had chosen hours as the estimation unit, the spread of answers would have been wider, and I’m not sure whether to bet on 7 (hours in a working day) or 10 being the most common choice.
Fitting a regression model to the student data shows estimates increasing by 0.4 weeks per year of degree progression. I was initially baffled by this, and then I realized that more experienced students expect to be given tougher problems to solve, i.e., this increase is based on self-image (code+data).
The stated hypothesis investigated by the study involved none of the above. Rather, the intent was to measure the impact of obsolete requirements on estimates. Subjects were randomly divided into three groups, with each seeing and estimating one specification. One specification contained four tasks (A), one contained five tasks (B), and one contained the same tasks as (A) plus an additional task followed by the sentence: “Please note that R5 should NOT be implemented” (C).
A regression model shows that for students and professions the estimate for (A) is about 1-2 weeks lower than (B), while (A) estimates are 3-5 weeks lower than (C) estimated.
What are subjects to make of an experimental situation where the specification includes a task that they are explicitly told to ignore?
How would you react? My first thought was that the ignore R5 sentence was itself ignored, either accidentally or on purpose. But my main thought is that Relevance theory is a complicated subject, and we are a very long way away from applying it to estimation experiments containing supposedly redundant information.
The plot below shows the number of subjects making a given estimate, in days; exp0to2 were student subjects (dashed line joins estimate that include a half-hour value, solid line whole hour), exp3 MSc students, and exp4 professional developers (code+data):
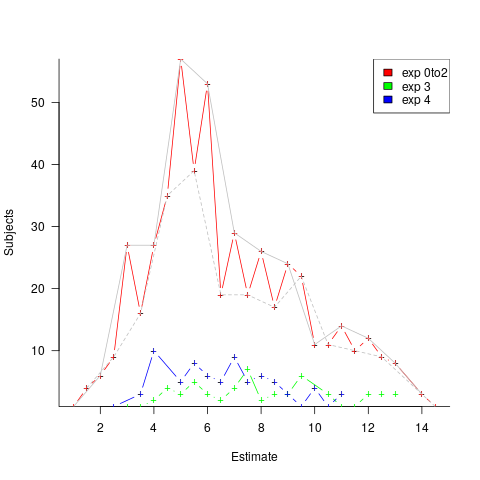
I hope that the authors of this study run more experiments, ideally working on the assumption that there is no connection between specification and estimate (apart from trivial examples).
Where are we with models of human learning?
Learning is an integral part of writing software. What have psychologists figured out about the characteristics of human learning?
A study of memory, published in 1885, kicked off the start of modern psychology research. At the start of the 1900s, learning research was still closely tied to the study of the characteristics of what we now call working memory, e.g., measuring the time taken for subjects to correctly recall sequences of digits, nonsense syllables, words and prose. By the 1930s, learning was a distinct subject in its own right.
What is now known as the power law of learning was first proposed in 1926. Wikipedia is right to use the phrase power law of practice, since it is some measure of practice that appears in the power law of learning equation: 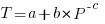 , where:
, where: 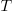 is the time taken to do the task,
is the time taken to do the task,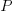 is some measure of practice (such as the number of times the subject has performed the task), and
is some measure of practice (such as the number of times the subject has performed the task), and  ,
,  , and
, and  are constants fitted to the data.
are constants fitted to the data.
For the next 70 years some form of power law did a good job of fitting the learning data produced by researchers. Then in 1997 a paper pointed out that researchers were fitting aggregate data (i.e., one equation fitted to all subject data), and that an exponential equation was a better fit to individual subject response times: 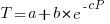 . The power law appeared to be the result of aggregating the exponential response performance of multiple subjects; oops.
. The power law appeared to be the result of aggregating the exponential response performance of multiple subjects; oops.
What is the situation today, 25 years later? Do the subsystems of our brains produce a power law or exponential improvement in performance, with practice?
The problem with answering this question is that both equations can fit the available data quite well, with one being a technically better fit than the other for different datasets. The big difference between the two equations is in their tails, however, it is costly and time-consuming to obtain enough data to distinguish between them in this region.
When discussing learning in my evidence-based software engineering book, I saw no compelling reason to run counter to the widely cited power law, but I did tell readers about the exponential fit issue.
Studies of learnings have tended to use simple tasks; subjects are usually only available for a short time, and many task repetitions are needed to model the impact of learning. Simple tasks tend to be dominated by one primary activity, which means that subjects can focus their learning on this one activity.
Complicated tasks involve many activities, each potentially providing distinct learning opportunities. Which activities will a subject focus on improving, will the performance on one activity improve faster than others, will the approach chosen for one activity limit the performance on a second activity?
For a complicated task, the change in performance with amount of practice could be a lot more complicated than a single power law/exponential equation, e.g., there may be multiple equations with each associated with one or more activities.
In the previous paragraph, I was careful to say “could be a lot more complicated”. This is because the few datasets of organizational learning show a power law performance improvement, e.g., from 1936 we have the most cited study Factors Affecting the Cost of Airplanes, and the less well known but more interesting Liberty shipbuilding from the 1940s.
If the performance of something involving multiple people performing many distinct activities follows a power law improvement with practice, then the performance of an individual carrying out a complicated task might follow a simple equation; perhaps the combined form of many distinct simple learning activities is a simple equation.
Researchers are now proposing more complicated models of learning, along with fitting them to existing learning datasets.
Which equation should software developers use to model the learning process?
I continue to use a power law. The mathematics tend to be straight-forward, and it often gives an answer that is good enough (because the data fitted contains lots of variance). If it turned out that an exponential would be easier to work with, I would be happy to switch. Unless there is a lot of data in the tail, the difference between power law/exponent is usually not worth worrying about.
There are situations where I have failed to successfully add a learning (power law) component to a model. Was this because there was no learning present, or was the learning not well-fitted by a power law? I don’t know, and I cannot think of an alternative equation that might work, for these cases.
How large an impact does social conformity have on estimates?
People experience social pressure to conform to group norms. How big an impact might social pressure have on a developer’s estimate of the effort needed to implement some functionality?
If a manager suggests that the effort likely to be required is large/small, I would expect a developer to respond accordingly (even if the manager is thought to be incompetent; people like to keep their boss happy). Of course, customer opinions are also likely to have an impact, but what about fellow team members, or even the receptionist. Until somebody runs the experiments, we are going to have to do with non-software related tasks.
A study by Molleman, Kurversa, and van den Bos asked subjects (102 workers on Mechanical Turk) to estimate the number of animals in an image (which contained between 50 and 100 ants, flamingos, bees, cranes or crickets). Subjects were given 30 seconds to respond, and after typing their answer they were told that “another participant had estimated X“, and given 45 seconds to give a second estimate. The ‘social pressure’ estimate, X, was chosen to be around 15-25% larger/smaller than the estimate given (values from a previous experiment were randomly selected).
The plot below shows the number of second estimates where there was a given percentage change between the first and second estimates, red line is a loess fit; the formula used is 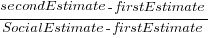 (code+data):
(code+data):
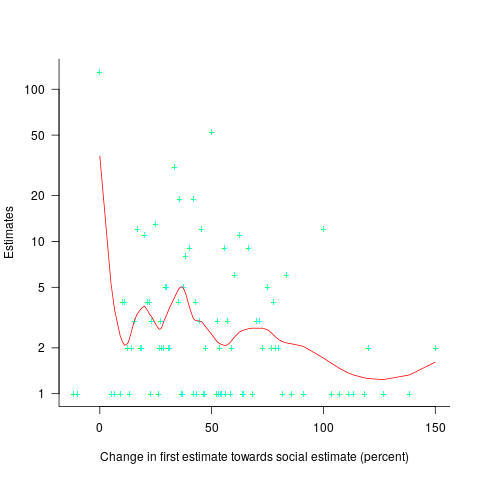
Around 25% of second estimates were unchanged, and 2% were changed to equal the social estimate. In two cases the second estimate was less than the first, and in eleven cases it was larger than the social estimate. Both the mean and median for shift towards the social estimate were just over 30% of the difference between the first estimate and the social estimate.
As with previous estimating studies, a few round numbers were often chosen. I was interested in finding out what impact the use of a round number value for the first estimate, or the social estimate, might have on the change in estimated value. The best regression model I could find showed that if the first estimate was exactly divisible by 5 (or 10), then the second estimate was likely to be around 5% larger. In fact divisible-by-5 was the only variable that had any predictive power.
My initial hypothesis was that the act of choosing a round number is an expression of uncertainty, and that this uncertainty increases the impact of the social estimate (when making the second estimate). An analysis of later experiments suggested that this pattern was illusionary (see below).
Modelling estimate values, rather than their differences, the equation: 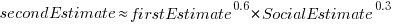 explains nearly all the variance present in the data.
explains nearly all the variance present in the data.
Two weeks after the first experiment, all 102 subjects were asked to repeat the experiment (they each saw the same images, in the same order, and social estimates as in the first study); 69 subjects participated. Nine months after the first experiment, subjects were asked to repeat the experiment again; 47 subjects participated, again with each subject seeing the same images in the same order, and social estimates. Thirty-five subjects participated in all three experiments.
To what extent were subjects consistently influenced by the social estimate, across three identical sessions? The Pearson correlation coefficient between both the first/second experiment, and the first/third experiment, was around 0.6.
The impact of round numbers was completely different, i.e., no impact on the second, and a -7% impact on the third (i.e., a reduced change). So much for my initial hypothesis.
The exponents in the above equation did not change much for the data from the second and third reruns of the experiment.
The variability in the social estimates used in these experiments, involving image contents, differs from software estimates in that they were only 12-25% different from the first estimate. Software estimates often differ by significantly larger amounts (in fact, a 12% difference would probably be taken as agreement).
With some teams, people meet to thrash out a team estimate. Data is sometimes available on the final estimate, but data on the starting values is very hard to come by. Pointers to experiments where social estimates are significantly different (i.e., greater than 50%) from the ones given by subjects welcome.
The Approximate Number System and software estimating
The ability to perform simple numeric operations can improve the fitness of a creature (e.g., being able to select which branch contains the most fruit), increasing the likelihood of it having offspring. Studies have found that a wide variety of creatures have a brain subsystem known as the Approximate Number System (ANS).
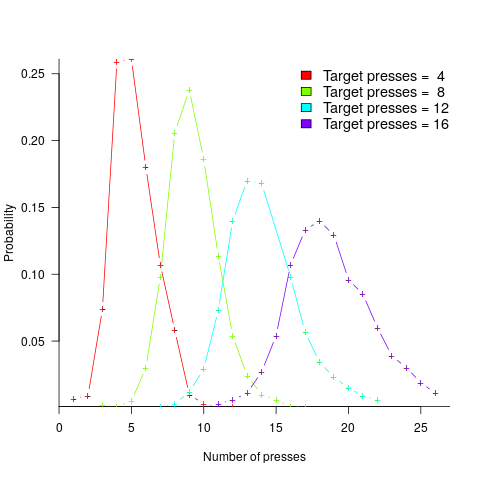
A study by Mechner rewarded rats with food, if they pressed a lever N times (with N taking one of the values 4, 8, 12 or 16), followed by pressing a second lever. The plot below shows the number of lever presses made before pressing the second lever, for a given required N; it suggests that the subject rat is making use of an approximate number system (code+data):
Humans have a second system for representing numbers, which is capable of exact representation, it is language. The Number Sense by Stanislas Dehaene was on my list of Christmas books for 2011.
One method used to study the interface between the two number systems, available to humans, involves subjects estimating the number of dots in a briefly presented image. While reading about one such study, I noticed that some of the plots showed patterns similar to the patterns seen in plots of software estimate/actual data. I emailed the lead author, Véronique Izard, who kindly sent me a copy of the experimental data.
The patterns I was hoping to see are those invariably seen in software effort estimation data, e.g., a power law relationship between actual/estimate, consistent over/under estimation by individuals, and frequent use of round numbers.
Psychologists reading this post may be under the impression that estimating the time taken to implement some functionality, in software, is a relatively accurate process. In practice, for short tasks (i.e., under a day or two) the time needed to form a more accurate estimate makes a good-enough estimate a cost-effective option.
This Izard and Dehaene study involved two experiments. In the first experiment, an image containing between 1 and 100 dots was flashed on the screen for 100ms, and subjects then had to type the estimated number of dots. Each of the six subjects participated in five sessions of 600 trials, with each session lasting about one hour; every number of dots between 1 and 100 was seen 30 times by each subject (for one subject the data contains 1,783 responses, other subjects gave 3,000 responses). Subjects were free to type any value as their estimate.
These kinds of studies have consistently found that subject accuracy is very poor (hardly surprising, given that subjects are not provided with any feedback to help calibrate their estimates). But since researchers are interested in patterns that might be present in the errors, very low accuracy is not an issue.
The plot below shows stimulus (number of dots shown) against subject response, with green line showing 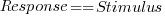 , and red line a fitted regression model having the form
, and red line a fitted regression model having the form 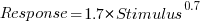 (which explains just over 70% of the variance; code+data):
(which explains just over 70% of the variance; code+data):
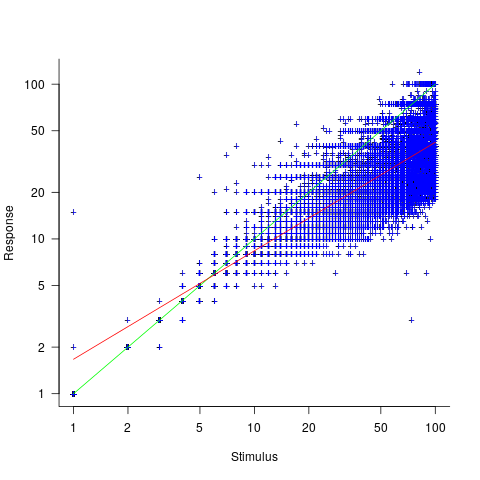
Just like software estimates, there is a good fit to a power law, and the only difference in accuracy performance is that software estimates tend not to be so skewed towards underestimating (i.e., there are a lot more low accuracy overestimates).
Adding subjectID to the model gives: 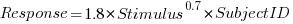 , with
, with 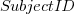 varying between 0.65 and 1.57; more than a factor of two difference between subjects (this model explains just under 90% of the variance). This is a smaller range than the software estimation data, but with only six subjects there was less chance of a wider variation (code+data).
varying between 0.65 and 1.57; more than a factor of two difference between subjects (this model explains just under 90% of the variance). This is a smaller range than the software estimation data, but with only six subjects there was less chance of a wider variation (code+data).
The software estimation data finds shows that accuracy does not improve with practice. The experimental subjects were not given any feedback, and would not be expected to improve, but does the strain of answering so many questions cause them to get worse? Adding trial number to the model suggests a 12% increase in underestimation, over 600 trials. However, adding an interaction with SubjectID shows that the performance of two subjects remains unchanged, while two subjects experience a 23% increase in underestimation.
The plot below shows the number of times each response was given, combining all subjects, with commonly given responses in red (code+data):
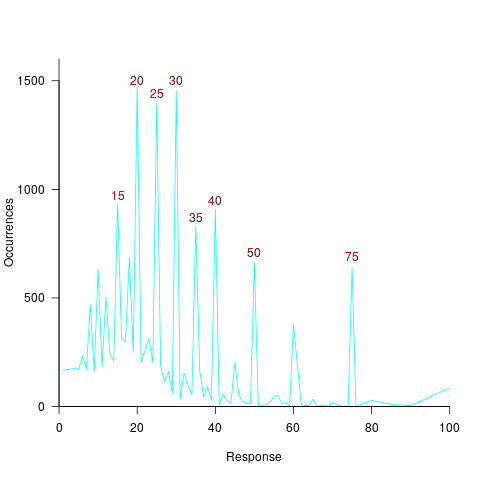
The commonly occurring values that appear in software estimation data are structured as fractions of units of time, e.g., 0.5 hours, or 1 hour or 1 day (appearing in the data as 7 hours). The only structure available to experimental subjects was subdivisions of powers of 10 (i.e., 10 and 100).
Analysing the responses by subject shows that each subject had their own set of preferred round numbers.
To summarize: The results from an experiment investigating the interface between the two human number systems contains three patterns seen in software estimation data, i.e., power law relationship between actual and estimate, individual differences in over/underestimating, and extensive use of round numbers.
Izard’s second experiment limited response values to prespecified values (i.e., one to 10 and multiples of 10), and gave a calibration example after each block of 46 trials. The calibration example improved performance, and the use of round numbers as prespecified response values had the effect of removing spikes from the response counts (which were relatively smooth; code+data)).
We now have circumstantial evidence that software developers are using the Approximate Number System when making software estimates. We will have to wait for brain images from a developer in an MRI scanner, while estimating a software task, to obtain more concrete proof that the ANS is involved in the process. That is, are the areas of the brain thought to be involved in the ANS (e.g., the intraparietal sulcus) active during software estimation?
Readability: a scientific approach
Readability, as applied to software development today, is a meaningless marketing term. Readability is promoted as a desirable attribute, and is commonly claimed for favored programming languages, particular styles of programming, or ways of laying out source code.
Whenever somebody I’m talking to, or listening to in a talk, makes a readability claim, I ask what they mean by readability, and how they measured it. The speaker invariably fumbles around for something to say, with some dodging and weaving before admitting that they have not measured readability. There have been a few studies that asked students to rate the readability of source code (no guidance was given about what readability might be).
If somebody wanted to investigate readability from a scientific perspective, how might they go about it?
The best way to make immediate progress is to build on what is already known. There has been over a century of research on eye movement during reading, and two model of eye movement now dominate, i.e., the E-Z Reader model and SWIFT model. Using eye-tracking to study developers is slowly starting to be adopted by researchers.
Our eyes don’t smoothly scan the world in front of us, rather they jump from point to point (these jumps are known as a saccade), remaining fixed long enough to acquire information and calculate where to jump next. The image below is an example from an eye tracking study, where subjects were asking to read a sentence (see figure 770.11). Each red dot appears below the center of each saccade, and the numbers show the fixation time (in milliseconds) for that point (code):

Models of reading are judged by the accuracy of their predictions of saccade landing points (within a given line of text), and fixation time between saccades. Simulators implementing the E-Z Reader and SWIFT models have found that these models have comparable performance, and the robustness of these models are compared by looking at the predictions they make about saccade behavior when reading what might be called unconventional material, e.g., mirrored or scarmbeld text.
What is the connection between the saccades made by readers and their understanding of what they are reading?
Studies have found that fixation duration increases with text difficulty (it is also affected by decreases with word frequency and word predictability).
It has been said that attention is the window through which we perceive the world, and our attention directs what we look at.
A recent study of the SWIFT model found that its predictions of saccade behavior, when reading mirrored or inverted text, agreed well with subject behavior.
I wonder what behavior SWIFT would predict for developers reading a line of code where the identifiers were written in camelCase or using underscores (sometimes known as snake_case)?
If the SWIFT predictions agreed with developer saccade behavior, a raft of further ‘readability’ tests spring to mind. If the SWIFT predictions did not agree with developer behavior, how might the model be updated to support the reading of lines of code?
Until recently, the few researchers using eye tracking to investigate software engineering behavior seemed to be having fun playing with their new toys. Things are starting to settle down, with some researchers starting to pay attention to existing models of reading.
What do I predict will be discovered?
Lots of studies have found that given enough practice, people can become proficient at handling some apparently incomprehensible text layouts. I predict that given enough practice, developers can become equally proficient at most of the code layout schemes that have been proposed.
The important question concerning text layout, is: which one enables an acceptable performance from a wide variety of developers who have had little exposure to it? I suspect the answer will be the one that is closest to the layout they have had the most experience,i.e., prose text.
Cognitive bias or not paying enough attention?
Assume you are responsible for two teams who independently work on projects, say Team A and Team B. The teams have different work completion rates, with Team A completing work at the rate of 70 widgets per week, while Team B completes 30 widgets per week. Both teams always work on projects that require the completion of the same number of widgets.
You have the resources to send just one of the teams on a course. It is predicted that sending Team A on the course would improve their performance to 110 widgets per week, while attending the course would improve the performance of Team B to 40 widgets per week.
Senior management have decreed that time to market is the metric by which project managers are judged.
You want to impress senior management by significantly improving time to market for your projects; which team do you send on the course (i.e., the one that is likely to experience the largest reduction in time to market)?
This question is a restatement of a one involving cars travelling at different speeds, that has grown into a niche research area. Studies have found that a large percentage of subjects give the wrong answer, and they are said to have a time-saving bias, or time-loss bias.
The inability to correctly process “inverse variables” has been given as the reason people tend to give the wrong answer. The term “inverse variables” comes from the formula for calculating completion time, where the velocity appears as the denominator. Another way of looking at this problem is that when going slowly, there is more scope for improvement, compared to when going much faster.
A speed increase from 30 to 40 is only 10, or a 33% improvement; while an increase from 70 to 110 is an increase of 40, or 57%. Based on these numbers, Team A should be sent on the course.
However, we are interested in time to market. Let’s assume that both teams have to complete a project requiring 100 widgets. Before attending the course, Team A completes 100 widgets in 100/70=1.4 weeks, and Team B completes 100 widgets in 100/30=3.3 weeks. After attending the course, Team A would complete 100 widgets in 100/110=0.91 weeks, and Team B would complete 100 widgets in 100/40=2.5 weeks. Time to market for Team A has been reduced by (1.4-0.9)=0.5 weeks, while the reduction for Team B is (3.3-2.5)=0.8 weeks. So sending Team B on the course makes you look better, on the time to market metric.
If somebody ran an experiment with project managers, would the subjects tend to incorrectly process “inverse variables”. Well, somebody has done the experiment, and yes, many subjects exhibited the time-saving bias (the experimental scenario described in the appendix is a lot easier to understand than the one in the main body of the paper, which is a mess; Magne Jørgensen continues to be the only person doing interesting experiments in software estimation).
It has become common practice that, when a large percentage of subjects in a psychology experiment respond in ways that are inconsistent with a mathematical approach, the behavior is labelled as being a bias. I think the use of this terminology makes the behavior sound more interesting than it actually is; what’s wrong with saying that people make mistakes. Perhaps labelling experimental responses as being a bias makes it easier to get papers published.
Whether people are biased, or don’t pay enough attention, when solving non-trivial equations, what might be done about it?
This is not about whether any particular metric is a useful one, rather it is about calculating the right answer for whatever metric happens to be chosen.
Would an awareness campaign highlighting the problems people have with “inverse variables” be worthwhile? I don’t think so. Many people have problems with equations, and I don’t see why this case is more worthy of being highlighted than any other.
Am I missing something?
Psychology researchers are interested in figuring out the functioning of the brain/mind, so they are looking for patterns in the responses subjects give. Once someone has published a few papers on a research topic, they become invested in it. If they continue to get funding, the papers keep on coming. Sometimes a niche topic acquires a major following, and the work contributes to a major change of thinking about the mind, e.g., the Wason selection task helped increase the evidence that culture has an impact on cognitive behavior.
I think that software engineering researchers need to carefully evaluate the likely importance of behaviors that psychology researchers have labelled as a bias.
Impact of native language on variable naming
When creating a variable name, to what extent are developers influenced by their native human language?
There is lots of evidence that variable names are either English words, abbreviations of English words, or some combination of these two. Source code containing a large percentage of identifiers using words from other languages does exist, but it requires effort to find; there is a widely expressed view that source should be English based (based on my experience of talking to non-native English speakers, and even the odd paper discussing the issue, e.g., Language matters).
Given that variable names can prove information that reduces the effort needed to understand code, and that most code is only ever read by the person who wrote it, developers should make the most of their expertise in using their native language.
To what extent do non-native English-speaking developers make use of their non-English native language?
I have found it very difficult to even have a discussion around this question. When I broach the subject with non-native English speakers, the response is often along the lines of “our develo0pers speak good English.” I am careful to set the scene by telling them of my interest in naming, and that I think there are benefits for developers to make use of their native language. The use of non-English languages in software development is not yet a subject that is open for discussion.
I knew that sooner or later somebody would run an experiment…
How Developers Choose Names is another interesting experiment involving Dror Feitelson (the paper rather confusingly refers to it as a survey, a post on an earlier experiment).
What makes this experiment interesting is that bilingual subjects (English and Hebrew) were used, and the questions were in English or Hebrew. The 230 subjects (some professional, some student) were given a short description and asked to provide an appropriate variable/function/data-structure name; English was used for 26 of the question, and Hebrew for the other 21 questions, and subjects answered a random subset.
What patterns of Hebrew usage are present in the variable names?
Out of 2017 answers, 14 contained Hebrew characters, i.e., not enough for statistical analysis. This does not mean that all the other variable names were only derived from English words, in some cases Hebrew words appeared via transcription using the 26 English letters. For instance, using “pinuk” for the Hebrew word that means “benefit” in English. Some variables were created from a mixture of Hebrew and English words, e.g., deservedPinuks and pinuksUsed.
Analysing this data requires someone who is fluent in Hebrew and English. I am not a fluent, or even non-fluent, Hebrew speaker. My role in this debate is encouraging others, and at last I have some interesting data to show people.
The paper spends time showing how for personal preferences result in a wide selection of names being chosen by different people for the same quantity. I cannot think of any software engineering papers that have addressed this issue for variable names, but there is lots of evidence from other fields; also see figure 7.33.
Those interested in searching source code for the impact of native-language might like to look at the names of variables appearing as operands of the bitwise and logical operators. Some English words occur much more frequently in the names of these variable, compared to variables that are operands of arithmetic operators, e.g., flag, status, and signal. I predict that non-native English-speaking developers will make use of corresponding non-English words.
Recent Comments