Historians of computing
Who are the historians of computing? The requirement I used for deciding who qualifies (for this post), is that the person has written multiple papers on the subject over a period that is much longer than their PhD thesis (several people have written a history of some aspect of computing PhDs, and then gone on to research other areas).
Maarten Bullynck. An academic who is a historian of mathematics and has become interested in software; use HAL to find his papers, e.g., What is an Operating System? A historical investigation (1954–1964).
Martin Campbell-Kelly. An academic who has spent his research career investigating computing history, primarily with a software orientation. Has written extensively on a wide variety of software topics. His book “From Airline Reservations to Sonic the Hedgehog: A History of the Software Industry” is still on my pile of books waiting to be read (but other historian cite it extensively). His thesis: “Foundations of computer programming in Britain, 1945-55″, can be freely downloadable from the British Library; registration required.
Paul E. Ceruzzi. An academic and museum curator; interested in aeronautics and computers. I found the one book of his that I have read, ok; others might like it more than me. Others cite him, and he wrote an interesting paper on Konrad Zuse (The Early Computers of Konrad Zuse, 1935 to 1945).
James W. Cortada. Ex-IBM (1974-2012) and now working at the Charles Babbage Institute. Written extensively on the history of computing. More of a hardware than software orientation. Written lots of detail oriented books and must have pole position for most extensive collection of material to cite (his end notes are very extensive). His “The Digital Flood: The Diffusion of Information Technology Across the U.S., Europe, and Asia” is likely to be the definitive work on the subject for some time to come. For me this book is spoiled by the author towing the company line in his analysis of the IBM antitrust trial; my analysis of the work Cortada cites reaches the opposite conclusion.
Nathan Ensmenger. An academic; more of a people person than hardware/software. His paper Letting the Computer Boys Take Over contains many interesting insights. His book The Computer Boys Take Over Computers, Programmers, and the Politics of Technical Expertise is a combination of topics that have been figured out, backed-up with references, and topics still being figured out (I wish he would not cite Datamation, a trade mag back in the day, so often).
Kenneth S. Flamm. An academic who has held senior roles in government. Writes from a industry evolution, government interests, economic perspective. The books: “Targeting the Computer: Government Support and International Competition” and “Creating the Computer: Government, Industry and High Technology” are packed with industry related economic data and covers all the major industrial countries.
Michael S. Mahoney. An academic who is sadly no longer with us. A historian of mathematics before becoming primarily involved with software history.
Jeffrey R. Yost. An academic. I have only read his book “Making IT Work: A history of the computer services industry”, which was really a collection of vignettes about people, companies and events; needs some analysis. Must try to track down some of his papers (which are not available via his web page :-(.
Who have I missed? This list is derived from papers/books I have encountered while working on a book, not an active search for historians. Suggestions welcome.
Updates
Completely forgot Kenneth S. Flamm, despite enjoying both his computer books.
Forgot Paul E. Ceruzzi because I was unimpressed by his “A History of Modern Computing”. Perhaps his other books are better.
Building a regression model is easy and informative
Running an experiment is very time-consuming. I am always surprised that people put so much effort into gathering the data and then spend so little effort analyzing it.
The Computer Language Benchmarks Game looks like a fun benchmark; it compares the performance of 27 languages using various toy benchmarks (they could not be said to be representative of real programs). And, yes, lots of boxplots and tables of numbers; great eye-candy, but what do they all mean?
The authors, like good experimentalists, make all their data available. So, what analysis should they have done?
A regression model is the obvious choice and the following three lines of R (four lines if you could the blank line) build one, providing lots of interesting performance information:
cl=read.csv("Computer-Language_u64q.csv.bz2", as.is=TRUE)
cl_mod=glm(log(cpu.s.) ~ name+lang, data=cl)
summary(cl_mod) |
The following is a cut down version of the output from the call to summary, which summarizes the model built by the call to glm.
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.299246 0.176825 7.348 2.28e-13 ***
namechameneosredux 0.499162 0.149960 3.329 0.000878 ***
namefannkuchredux 1.407449 0.111391 12.635 < 2e-16 ***
namefasta 0.002456 0.106468 0.023 0.981595
namemeteor -2.083929 0.150525 -13.844 < 2e-16 ***
langclojure 1.209892 0.208456 5.804 6.79e-09 ***
langcsharpcore 0.524843 0.185627 2.827 0.004708 **
langdart 1.039288 0.248837 4.177 3.00e-05 ***
langgcc -0.297268 0.187818 -1.583 0.113531
langocaml -0.892398 0.232203 -3.843 0.000123 ***
Null deviance: 29610 on 6283 degrees of freedom
Residual deviance: 22120 on 6238 degrees of freedom
What do all these numbers mean?
We start with glm's first argument, which is a specification of the regression model we are trying to fit: log(cpu.s.) ~ name+lang
cpu.s. is cpu time, name is the name of the program and lang is the language. I found these by looking at the column names in the data file. There are other columns in the data, but I am running in quick & simple mode. As a first stab, I though cpu time would depend on the program and language. Why take the log of the cpu time? Well, the model fitted using cpu time was very poor; the values range over several orders of magnitude and logarithms are a way of compressing this range (and the fitted model was much better).
The model fitted is:
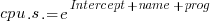 , or
, or 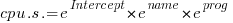
Plugging in some numbers, to predict the cpu time used by say the program chameneosredux written in the language clojure, we get: 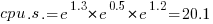 (values taken from the first column of numbers above).
(values taken from the first column of numbers above).
This model assumes there is no interaction between program and language. In practice some languages might perform better/worse on some programs. Changing the first argument of glm to: log(cpu.s.) ~ name*lang, adds an interaction term, which does produce a better fitting model (but it's too complicated for a short blog post; another option is to build a mixed-model by using lmer from the lme4 package).
We can compare the relative cpu time used by different languages. The multiplication factor for clojure is 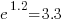 , while for
, while for ocaml it is 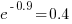 . So
. So clojure consumes 8.2 times as much cpu time as ocaml.
How accurate are these values, from the fitted regression model?
The second column of numbers in the summary output lists the estimated standard deviation of the values in the first column. So the clojure value is actually 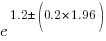 , i.e., between 2.2 and 4.9 (the multiplication by 1.96 is used to give a 95% confidence interval); the
, i.e., between 2.2 and 4.9 (the multiplication by 1.96 is used to give a 95% confidence interval); the ocaml values are 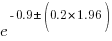 , between 0.3 and 0.6.
, between 0.3 and 0.6.
The fourth column of numbers is the p-value for the fitted parameter. A value of lower than 0.05 is a common criteria, so there are question marks over the fit for the program fasta and language gcc. In fact many of the compiled languages have high p-values, perhaps they ran so fast that a large percentage of start-up/close-down time got included in their numbers. Something for the people running the benchmark to investigate.
Isn't it easy to get interesting numbers by building a regression model? It took me 10 minutes, ok I spend a lot of time fitting models. After spending many hours/days gathering data, spending a little more time learning to build simple regression models is well worth the effort.
Statement sequence length for error/non-error paths
One of the folk truisms of the compiler/source code analysis business is that error paths are short, i.e., when an error situation is detected (such as failing to open a file), few statements are executed before the functions returns.
Having repeated this truism for many decades, figure 2 from the paper APEx: Automated Inference of Error Specifications for C APIs jumped off the page at me; thanks to Yuan Kang, I now have a copy of the data.
The plots below (code+data) show two representations of the non-error/error path lengths (measured in statements within individual functions of libc; counting starts at a library call that could return an error value). The upper plot shows statement sequence lengths for error/non-error paths, and the lower is a kernel density plot of the error/non-error sequence lengths.
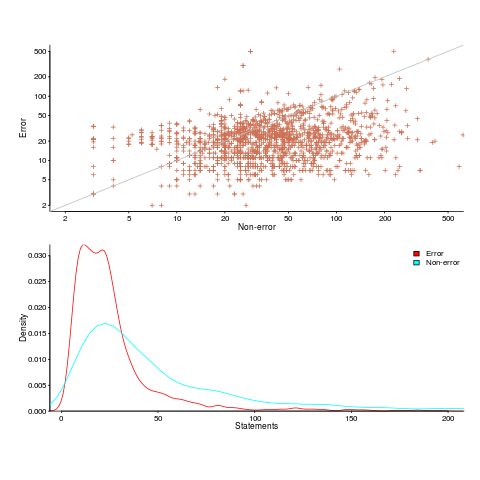
Another truism is that people tend to write positive tests, i.e., tests that do not involve error handling (some evidence).
Code coverage measurements (e.g., number of statements or branches that are executed by a test suite) often show the pattern seen in the plot below (code+data; thanks to the authors of the paper Code Coverage for Suite Evaluation by Developers for making the data available). The data was obtained by measuring the coverage of 1,043 Java programs executing their associated test suite (circles denote program size). Lines are fitted regression models for different sized programs.
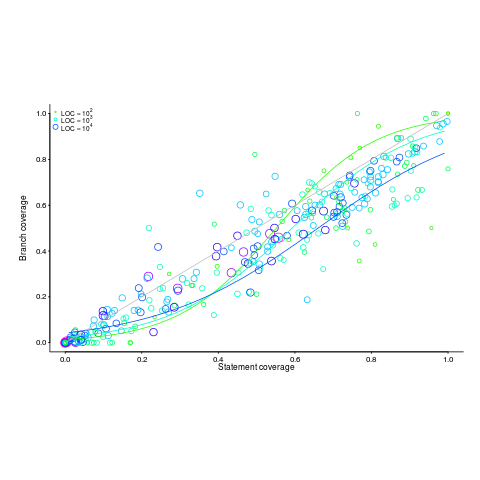
If people are preferentially writing positive tests, test suites with low coverage would be expected to execute a greater percentage of statements than branches (an if-statement has two branches, taken/not-taken), i.e., the behavior seen in the plot above (grey line shows equal statement/branch coverage). Once the low hanging fruit is tested (i.e., the longer, non-error, cases), tests have to be written for the shorter, more likely to be error handling, cases.
The plot would also be explained by typical execution paths favoring longer basic blocks, but I don’t have any data that could show this one way or another.
Mathematical proofs contain faults, just like software
The idea of proving programs correct, like mathematical proofs, is appealing, but is based on an incorrect assumption often made by non-mathematicians, e.g., mathematical proofs are fault free. In practice, mathematicians make mistakes and create proofs that contain serious errors; those of us who are taught mathematical techniques, but are not mathematicians, only get to see the good stuff that has been checked over many years.
An appreciation that published proofs contain mistakes is starting to grow, but Magnificent mistakes in mathematics is an odd choice for a book title on the topic. Quotes from De Millo’s article on “Social Processes and Proofs of Theorems and Programs” now appear regularly; On proof and progress in mathematics is worth a read.
Are there patterns to the faults that appear in claimed mathematical proofs?
- The difficulty of the problem is one obvious issue, as shown by the faulty proofs of the N vs. NP problem,
- the size of the proof, in number of pages, is a common problem, with Mochizuki’s ‘proof’ of the ABC conjecture being a recent example and the Hales-Ferguson proof of the Kepler conjecture has a whole book dedicated to trying to figure out if the proof is correct,
- number of people involved: some of the 100+ mathematicians responsible for proving components of the classification of finite simple groups died before the proof was claimed to be complete; the proofs of the various components created the largest known claimed proof, at tens of thousands of pages.
A surprisingly common approach, used by mathematicians to avoid faults in their proofs, is to state theorems without giving a formal proof (giving an informal one is given instead). There are plenty of mathematicians who don’t think proofs are a big part of mathematics (various papers from the linked-to book are available as pdfs).
Next time you encounter an advocate of proving programs correct using mathematics, ask them what they think about the uncertainty about claimed mathematical proofs and all the mistakes that have been found in published proofs.
Compiler validation is now part of history
Compiler validation makes sense in a world where there are many different hardware platforms, each with their own independent compilers (third parties often implemented compilers for popular platforms, competing against the hardware vendor). A large organization that spends hundreds of millions on a multitude of computer systems (e.g., the U.S. government) wants to keep prices down, which means the cost of porting its software to different platforms needs to be kept down (or at least suppliers need to think it will not cost too much to switch hardware).
A crucial requirement for source code portability is that different compilers be able to compile the same source, generating code that produces the same behavior. The same behavior requirement is an issue when the underlying word-size varies or has different alignment requirements (lots of code relies on data structures following particular patterns of behavior), but management on all sides always seems to think that being able to compile the source is enough. Compilers vendors often supported extensions to the language standard, and developers got to learn they were extensions when porting to a different compiler.
The U.S. government funded a conformance testing service, and paid for compiler validation suites to be written (source code for what were once the Cobol 85, Fortran 78 and SQL validation suites). While it was in business, this conformance testing service was involved C compiler validation, but it did not have to fund any development because commercial test suites were available.
The 1990s was the mass-extinction decade for companies selling non-Intel hardware. The widespread use of Open source compilers, coupled with the disappearance of lots of different cpus (porting compilers to new vendor cpus was always a good money spinner, for the compiler writing cottage industry), meant that many compilers disappeared from the market.
These days, language portability issues have been essentially solved by a near monoculture of compilers and cpus. It’s the libraries that are the primary cause of application portability problems. There is a test suite for POSIX and Linux has its own tests.
There are companies selling compiler C/C++ test suites (e.g., Perennial and PlumHall); when maintaining a compiler, it’s cost-effective to have a set of third-party tests designed to exercise all the language.
The OpenGroup offer to test your C compiler and issue a brand certificate if it passes the tests.
Source code portability requires compilers to have the same behavior and traditionally the generally accepted behavior has been defined by an ISO Standard or how one particular implementation behaved. In an Open source world, behavior is defined by what needs to be done to run the majority of existing code. Does it matter if Open source compilers evolve in a direction that is different from the behavior specified in an ISO Standard? I think not, it makes no difference to the majority of developers; but be careful, saying this can quickly generate a major storm in a tiny teacup.
What instructions should a computer support?
The modern answer to what instructions should a computer support is: lots (e.g., many kinds of: add, subtract, compare, branch, load, store, etc). John von Neumann’s famous First Draft of a Report on the EDVAC, written in 1945, specifies 97 instructions (later, actual implementations contained fewer instructions) and modern Intel processors contain several thousand instructions.
The Turing machine has a very simple instruction set; the machine is driven by a lookup table that specifies one or more of the operations: erase/write a symbol (to the cell currently under the read/write head), move the read/write head left or right (on a tape containing cells), and load a new state (which may be the same as the current one).
When computers were new, the lure of creating a minimalist instruction set had theoretical and practical appeal (valve computers were large and unreliable, reducing the number of components improved reliability and reduced costs).
The design of the IAS machine, built in the late 1940s, was based on von Neumann’s design. Haskell Curry came up with a minimalist set of four instructions that could be used to implement its supported instructions (the idea was that programs would be stored in minimalist form to reduce storage overheads).
Minimalist instruction sets still have theoretical appeal.
Simplicity (rather than minimalism) became fashionable in the 1980s with RISC. This was a reaction to the implementation/runtime costs of very complicated of instructions found in DEC’s VAX and later Motorola’s 68000 processors. Supporting these complicated instructions generated additional overhead for the simpler instructions (which is what most programs spent most of their time executing). The idea behind RISC was that simplifying the instruction set would reduce cpu design costs, improve performance (by making simple instructions fast); leaving the complicated stuff to be supported via software.
Starting out with ‘simple’ MIPS, RISC cpus got successively more complicated with SPARC, Motorola’s MC88000 and then IBM’s RS/6000. I worked on code generators for the SPARC and MC88000 and found them somewhat dull after working on CISC processors. There were huge arguments around RISC vs. CISC (I suspect that many of those involved had never used a RISC processor), but then this was back in the days when many programmers knew a lot of the technical details about the processors they used. (How many of today’s programmers can name the Intel x86 registers?)
More background on 1950s minimalism in the paper: Less is more in the Fifties. Encounters between Logical Minimalism and Computer Design during the 1950s.
These days, people are inventing very different architectures within which existing instructions have to operate, rather than radically new instructions.
Learning a cpu’s instruction set
A few years ago I wrote about the possibility of secret instruction sets making a comeback and the minimum information needed to write a code generator. A paper from the sporadic (i.e., they don’t release umpteen slices of the same overall paper), but always interesting, group at Stanford describes a tool that goes a long way to solving the secret instruction set problem; stratified synthesis learns an instruction set, starting from a small set of known instructions.
After feeding in 51 base instructions and 11 templates, 1,795.42 instruction ‘formulas’ were learned (119.42 were 8-bit constant instructions, every variant counted as 1/256 of an instruction); out of a maximum of 3,683 possible instructions (depending on how you count instructions).
As well as discovering ‘new’ instructions, they also discovered bugs in the Intel 64 and IA-32 Architectures Software Developer Manuals. In my compiler writing days, bugs in cpu documentation were a pet hate (they cause huge amounts of time to be wasted).
The initial starting information used is rather large, from the perspective of understanding the instruction set of an unknown cpu. I’m sure others will be working to reduce the necessary startup information needed to obtain useful results. The Intel Management Engine is an obvious candidate for investigation.
Vendors sometimes add support for instructions without publicizing them and sometimes certain bit patterns happen to do something sensible in a particular version of a design because some random pattern of bits happens to do whatever it does without being treated as an illegal opcode. Your journey down the rabbit hole starts here.
On a related note, I continue to be amazed that widely used disassemblers fail to correctly handle surprisingly many, documented, x86 opcodes; benchmarks from 2010 and 2016
First use of: software, software engineering and source code
While reading some software related books/reports/articles written during the 1950s, I suddenly realized that the word ‘software’ was not being used. This set me off looking for the earliest use of various computer terms.
My search process consisted of using pfgrep on my collection of pdfs of documents from the 1950s and 60s, and looking in the index of the few old computer books I still have.
Software: The Oxford English Dictionary (OED) cites an article by John Tukey published in the American Mathematical Monthly during 1958 as the first published use of software: “The ‘software’ comprising … interpretive routines, compilers, and other aspects of automotive programming are at least as important to the modern electronic calculator as its ‘hardware’.”
I have a copy of the second edition of “An Introduction to Automatic Computers” by Ned Chapin, published in 1963, which does a great job of defining the various kinds of software. Earlier editions were published in 1955 and 1957. Did these earlier edition also contain various definitions of software? I cannot find any reasonably prices copies on the second-hand book market. Do any readers have a copy?
Update: I now have a copy of the 1957 edition of Chapin’s book. It discusses programming, but there is no mention of software.
Software engineering: The OED cites a 1966 “letter to the ACM membership” by Anthony A. Oettinger, then ACM President: “We must recognize ourselves … as members of an engineering profession, be it hardware engineering or software engineering.”
The June 1965 issue of COMPUTERS and AUTOMATION, in its Roster of organizations in the computer field, has the list of services offered by Abacus Information Management Co.: “systems software engineering”, and by Halbrecht Associates, Inc.: “software engineering”. This pushes the first use of software engineering back by a year.
Source code: The OED cites a 1965 issue of Communications ACM: “The PUFFT source language listing provides a cross-reference between the source code and the object code.”
The December 1959 Proceedings of the EASTERN JOINT COMPUTER CONFERENCE contains the article: “SIMCOM – The Simulator Compiler” by Thomas G. Sanborn. On page 140 we have: “The compiler uses this convention to aid in distinguishing between SIMCOM statements and SCAT instructions which may be included in the source code.”
Update: The October 1956 issue of Computers and Automation contains an extensive glossary. It does not have any entries for software or source code.
Running pdfgrep over the archive of documents on bitsavers would probably throw up all manners of early users of software related terms.
The paper: What’s in a name? Origins, transpositions and transformations of the triptych Algorithm -Code -Program is a detailed survey of the use of three software terms.
Computer books your great grandfather might have read
I have been reading two very different computer books written for a general readership: Giant Brains or Machines that Think, published in 1949 (with a retrospective chapter added in 1961) and LET ERMA DO IT, published in 1956.
‘Giant Brains’ by Edmund Berkeley, was very popular in its day.
Berkeley marvels at a computer performing 5,000 additions per second; performing all the calculations in a week that previously required 500 human computers (i.e., people using mechanical adding machines) working 40 hours per week. His mind staggers at the “calculating circuits being developed” that can perform 100,00 additions a second; “A mechanical brain that can do 10,000 additions a second can very easily finish almost all its work at once.”
The chapter discussing the future, “Machines that think, and what they might do for men”, sees Berkeley struggling for non-mathematical applications; a common problem with all new inventions. Automatic translator and automatic stenographer (typist who transcribe dictation) are listed. There is also a chapter on social control, which is just as applicable today.
This was the first widely read book to promote Shannon‘s idea of using the algebra invented by George Boole to analyze switching circuits symbolically (THE 1940 Masters thesis).
The ‘ERMA’ book paints a very rosy picture of the future with computer automation removing the drudgery that so many jobs require; it is so upbeat. A year later the USSR launched Sputnik and things suddenly looked a lot less rosy.
Added two more books
Cybernetics Or Communication And Control In The Animal And The Machine by Norbert Wiener
The Organization Of Behavior A Neuropsychological Theory by D. O. Hebb
and another
The Preparation of Programs for an Electronic Digital Computer by Wilkes, Wheeler, Gill (the link is to the 1957 second edition, not the 1951 first edition)
Was a C90, C99, or C11 compiler used?
How can a program figure out whether it has been compiled with a C90, C99 or C11 compiler?
Support for the // style of commenting was added in C99.
Support for Unicode string literals (e.g., U"Hello World") was added in C11.
Putting these together we get the following:
#include <stdio.h> #define M(U) sizeof(U"s"[0]) int main(void) { switch(M("")*2 //**/ 2 ) { case 1: printf("C90\n"); break; case 2: printf("C99\n"); break; case 8: printf("C11\n"); break; } } |
Recent Comments