Archive
Time-to-fix when mistake discovered in a later project phase
Traditionally the management of software development projects divides them into phases, e.g., requirements, design, coding and testing. A mistake introduced in one phase may not be detected until a later phase. There is long-standing folklore that earlier mistakes detected in later phases are much much more costly to fix persists, despite the original source of this folklore being resoundingly debunked. Fixing a mistake later is likely to a bit more costly, but how much more costly? A lack of data prevents reliable analysis; this question also suffers from different projects having different cost-to-fix profiles.
This post addresses the time-to-fix question (cost involves all the resources needed to perform the fix). Does it take longer to correct mistakes when they are detected in phases that come after the one in which they were made?
The data comes from the paper: Composing Effective Software Security Assurance Workflows. The 35,367 (yes, thirty-five thousand) logged fixes, from 39 projects drawn from three organizations, contains information on: phases in which the mistake was made and fixed, time taken, person ID, project ID, date/time, plus other stuff 🙂
Every project has its own characteristics that affect time-to-fix. Project 615, avionics software developed by organization A, has the most fixes (7,503) and is analysed here.
Avionics software is safety critical, and each major phase included its own review and inspection. The major phases include: requirements gathering, requirements analysis, high level design, design, coding, and testing. When counting the number of phases between introduction/fix, should review and inspection each count as a phase?
The primary reason for doing a review and inspection is to check the correctness (i.e., lack of mistakes) in the corresponding phase. If there is a time-to-fix penalty for mistakes found in these symbiotic-phases, I suspect it will be different from the time-to-fix penalty between major phases (which for simplicity, I’m assuming is major-phase independent).
The time-to-fix has a resolution of 1-minute, and some fix times are listed as taking a minute; 72% of fixes are recorded as taking less than 10-minutes. What kind of mistakes require less than 10-minutes to fix? Typos and other minutiae.
The plot below shows time-to-fix for mistakes having a given ‘distance’ between introduction/fix phase, for fixes taking at least 1, 5 and 10-minutes (code+data):
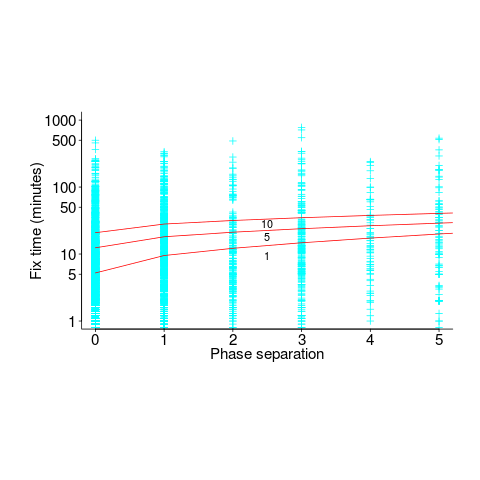
There is a huge variation in time-to-fix, and the regression lines (which have the form: 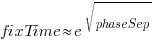 ) explains just 6% of the variance in the data, i.e., there is a small increase with phase separation, but it is almost down in the noise.
) explains just 6% of the variance in the data, i.e., there is a small increase with phase separation, but it is almost down in the noise.
All but one of the 38 people who worked on the project made multiple fixes (30 made more than 20 fixes), and may have got faster with practice. Adding the number of previous fixes by people making more than 20 fixes to the model gives: 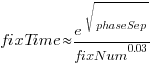 , and improves the model by less than 1-percent.
, and improves the model by less than 1-percent.
Fixing mistakes is a human activity, and individual performance often has a big impact on fitted models. Adding person ID to the model as a multiplication factor: i.e., 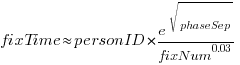 , improves the variance explained to 14% (better than a poke in the eye, just). The fitted value of
, improves the variance explained to 14% (better than a poke in the eye, just). The fitted value of  varies between 0.66 and 1.4 (factor of two, human variation).
varies between 0.66 and 1.4 (factor of two, human variation).
The answer to the time-to-fix question posed earlier (for project 615), is that it does take slightly longer to fix a mistake detected in phases occurring after the one in which the mistake was introduced. The phase difference is tiny, with differences in human performance having a bigger impact.
Quality control in a zero cost of replication business
When a new manufacturing material becomes available, its use is often integrated with existing techniques, e.g., using scientific management techniques for software production.
Customers want reliable products, and companies that sell unreliable products don’t make money (and may even lose lots of money).
Quality assurance of manufactured products is a huge subject, and lots of techniques have been developed.
Needless to say, quality assurance techniques applied to the production of hardware are often touted (and sometimes applied) as the solution for improving the quality of software products (whatever quality is currently being defined as).
There is a fundamental difference between the production of hardware and software:
- Hardware is designed, a prototype made and this prototype refined until it is ready to go into production. Hardware production involves duplicating an existing product. The purpose of quality control for hardware production is ensuring that the created copies are close enough to identical to the original that they can be profitably sold. Industrial design has to take into account the practicalities of mass production, e.g., can this device be made at a low enough cost.
- Software involves the same design, prototype, refinement steps, in some form or another. However, the final product can be perfectly replicated at almost zero cost, e.g., downloadable file(s), burn a DVD, etc.
Software production is a once-off process, and applying techniques designed to ensure the consistency of a repetitive process don’t sound like a good idea. Software production is not at all like mass production (the build process comes closest to this form of production).
Sometimes people claim that software development does involve repetition, in that a tiny percentage of the possible source code constructs are used most of the time. The same is also true of human communications, in that a few words are used most of the time. Does the frequent use of a small number of words make speaking/writing a repetitive process in the way that manufacturing identical widgets is repetitive?
The virtually zero cost of replication (and distribution, via the internet, for many companies) does more than remove a major phase of the traditional manufacturing process. Zero cost of replication has a huge impact on the economics of quality control (assuming high quality is considered to be equivalent to high reliability, as measured by number of faults experienced by customers). In many markets it is commercially viable to ship software products that are believed to contain many mistakes, because the cost of fixing them is so very low; unlike the cost of hardware, which is non-trivial and involves shipping costs (if only for a replacement).
Zero defects is not an economically viable mantra for many software companies. When companies employ people to build the same set of items, day in day out, there is economic sense in having them meet together (e.g., quality circles) to discuss saving the company money, by reducing production defects.
Many software products have a short lifespan, source code has a brief and lonely existence, and many development projects are never shipped to paying customers.
In software development companies it makes economic sense for quality circles to discuss the minimum number of known problems they need to fix, before shipping a product.
Extreme value theory in software engineering
As its name suggests, extreme value theory deals with extreme deviations from the average, e.g., how often will rainfall be heavy enough to cause a river to overflow its banks.
The initial list of statistical topics I thought ought to be covered in my evidence-based software engineering book included extreme value theory. At the time, and even today, there were/are no books covering “Statistics for software engineering”, so I had no prior work to guide my selection of topics. I was keen to cover all the important topics, had heard of it in several (non-software) contexts and jumped to the conclusion that it must be applicable to software engineering.
Years pass: the draft accumulate a wide variety of analysis techniques applied to software engineering data, but, no use of extreme value theory.
Something else does not happen: I don’t find any ‘Using extreme value theory to analyse data’ books. Yes, there are some really heavy-duty maths books available, but nothing of a practical persuasion.
The book’s Extreme value section becomes a subsection, then a subsubsection, and ended up inside a comment (I cannot bring myself to delete it).
It appears that extreme value theory is more talked about than used. I can understand why. Extreme events are newsworthy; rivers that don’t overflow their banks are not news.
Just over a month ago a discussion cropped up on the UK’s C++ standards’ panel mailing list: was email traffic down because of COVID-19? The panel’s convenor, Roger Orr, posted some data on monthly volumes. Oh, data 🙂
Monthly data is a bit too granular for detailed analysis over relatively short periods. After some poking around Roger was able to send me the date&time of every post to the WG21‘s Core and Lib reflectors, since February 2016 (there have been various changes of hosts and configurations over the years, and date of posts since 2016 was straightforward to obtain).
During our email exchanges, Roger had mentioned that every now and again a huge discussion thread comes out of nowhere. Woah, sounds like WG21 could do with some extreme value theory. How often are huge discussion threads likely to occur, and how huge is a once in 10-years thread that they might have to deal with?
There are two techniques for analysing the distribution of extreme values present in a sample (both based around the generalized extreme value distribution):
- Generalized Extreme Value (GEV) uses block maxima, e.g., maximum number of daily emails sent in each month,
- Generalized Pareto (GP) uses peak over threshold: pick a threshold and extract day values for when more than this threshold number of emails was sent.
The plots below show the maximum number of monthly emails that are expected to occur (y-axis) within a given number of months (x-axis), for WG21’s Core and Lib email lists. The circles are actual occurrences, and dashed lines 95% confidence intervals; GEV was used for these fits (code+data):
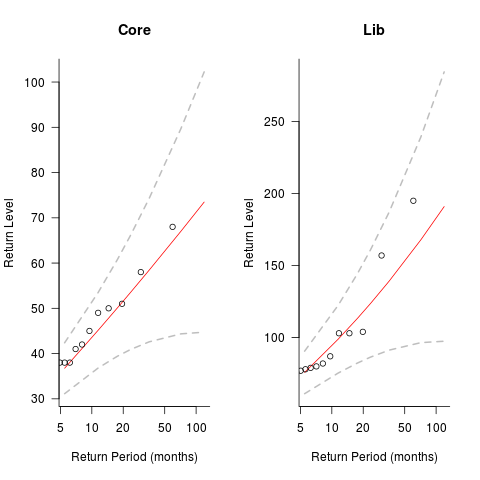
The 10-year return value for Core is around a daily maximum of 70 +-30, and closer to 200 +-100 for Lib.
The model used is very simplistic, and fails to take into account the growth in members joining these lists and traffic lost when a new mailing list is created for a new committee subgroup.
If any readers have suggests for uses of extreme value theory in software engineering, please let me know.
Postlude. This discussion has reordered events. My original interest in the mailing list data was the desire to find some evidence for the hypothesis that the volume of email increased as the date of the next WG21 meeting approached. For both Core and Lib, the volume actually decreases slightly as the date of the next meeting approaches; see code for details. Also, the volume of email at the weekend is around 60% lower than during weekdays.
Scientific management of software production
When Frederick Taylor investigated the performance of workers in various industries, at the start of the 1900’s, he found that workers organise their work to suit themselves; workers were capable of producing significantly more than they routinely produced. This was hardly news. What made Taylor’s work different was that having discovered the huge difference between actual worker output and what he calculated could be achieved in practice, he was able to change work practices to achieve close to what he had calculated to be possible. Changing work practices took several years, and the workers did everything they could to resist it (Taylor’s The principles of scientific management is an honest and revealing account of his struggles).
Significantly increasing worker output pushed company profits through the roof, and managers everywhere wanted a piece of the action; scientific management took off. Note: scientific management is not a science of work, it is a science of the management of other people’s work.
The scientific management approach has been successfully applied to production where most of the work can be reduced to purely manual activities (i.e., requiring little thinking by those who performed them). The essence of the approach is to break down tasks into the smallest number of component parts, to simplify these components so they can be performed by less skilled workers, and to rearrange tasks in a way that gives management control over the production process. Deskilling tasks increases the size of the pool of potential workers, decreasing labor costs and increasing the interchangeability of workers.
Given the almost universal use of this management technique, it is to be expected that managers will attempt to apply it to the production of software. The software factory was tried, but did not take-off. The use of chief programmer teams had its origins in the scarcity of skilled staff; the idea is that somebody who knows what they were doing divides up the work into chunks that can be implemented by less skilled staff. This approach is essentially the early stages of scientific management, but it did not gain traction (see “Programmers and Managers: The Routinization of Computer Programming in the United States” by Kraft).
The production of software is different in that once the first copy has been created, the cost of reproduction is virtually zero. The human effort invested in creating software systems is primarily cognitive. The division between management and workers is along the lines of what they think about, not between thinking and physical effort.
Software systems can be broken down into simpler components (assuming all the requirements are known), but can the implementation of these components be simplified such that they can be implemented by less skilled developers? The process of simplification is practical when designing a system for repetitive reproduction (e.g., making the same widget again and again), but the first implementation of anything is unlikely to be simple (and only one implementation is needed for software).
If it is not possible to break down the implementation such that most of the work is easy to do, can we at least hire the most productive developers?
How productive are different developers? Programmer productivity has been a hot topic since people started writing software, but almost no effective research has been done.
I have no idea how to measure programmer productivity, but I do have some ideas about how to measure their performance (a high performance programmer can have zero productivity by writing programs, faster than anybody else, that don’t do anything useful, from the client’s perspective).
When the same task is repeatedly performed by different people it is possible to obtain some measure of average/minimum/maximum individual performance.
Task performance improves with practice, and an individual’s initial task performance will depend on their prior experience. Measuring performance based on a single implementation of a task provides some indication of minimum performance. To obtain information on an individual’s maximum performance they need to be measured over multiple performances of the same task (and of course working in a team affects performance).
Should high performance programmers be paid more than low performance programmers (ignoring the issue of productivity)? I am in favour of doing this.
What about productivity payments, e.g., piece work?
This question is a minefield of issues. Manual workers have been repeatedly found to set informal quotas amongst themselves, i.e., setting a maximum on the amount they will produce during a shift (see “Money and Motivation: An Analysis of Incentives in Industry” by William Whyte). Thankfully, I don’t think I will be in a position to have to address this issue anytime soon (i.e., I don’t see a reliable measure of programmer productivity being discovered in the foreseeable future).
Surveys are fake research
For some time now, my default position has been that software engineering surveys, of the questionnaire kind, are fake research (surveys of a particular research field used to be worth reading, but not so often these days; that issues is for another post). Every now and again a non-fake survey paper pops up, but I don’t consider the cost of scanning all the fake stuff to be worth the benefit of finding the rare non-fake survey.
In theory, surveys could be interesting and worth reading about. Some of the things that often go wrong in practice include:
- poorly thought out questions. Questions need to be specific and applicable to the target audience. General questions are good for starting a conversation, but analysis of the answers is a nightmare. Perhaps the questions are non-specific because the researcher is looking for direction: well please don’t inflict your search for direction on the rest of us (a pointless plea in the fling it at the wall to see if it sticks world of academic publishing).
Questions that demonstrate how little the researcher knows about the topic serve no purpose. The purpose of a survey is to provide information of interest to those in the field, not as a means of educating a researcher about what they should already know,
- little effort is invested in contacting a representative sample. Questionnaires tend to be sent to the people that the researcher has easy access to, i.e., a convenience sample. The quality of answers depends on the quality and quantity of those who replied. People who run surveys for a living put a lot of effort into targeting as many of the right people as possible,
- sloppy and unimaginative analysis of the replies. I am so fed up with seeing an extensive analysis of the demographics of those who replied. Tables containing response break-down by age, sex, type of degree (who outside of academia cares about this) create a scientific veneer hiding the lack of any meaningful analysis of the issues that motivated the survey.
Although I have taken part in surveys in the past, these days I recommend that people ignore requests to take part in surveys. Your replies only encourage more fake research.
The aim of this post is to warn readers about the growing use of this form of fake research. I don’t expect anything I say to have any impact on the number of survey papers published.
Effort estimation’s inaccurate past and the way forward
Almost since people started building software systems, effort estimation has been a hot topic for researchers.
Effort estimation models are necessarily driven by the available data (the Putnam model is one of few whose theory is based on more than arm waving). General information about source code can often be obtained (e.g., size in lines of code), and before package software and open source, software with roughly the same functionality was being implemented in lots of organizations.
Estimation models based on source code characteristics proliferated, e.g., COCOMO. What these models overlooked was human variability in implementing the same functionality (a standard deviation that is 25% of the actual size is going to introduce a lot of uncertainty into any effort estimate), along with the more obvious assumption that effort was closely tied to source code characteristics.
The advent of high-tech clueless button pushing machine learning created a resurgence of new effort estimation models; actually they are estimation adjustment models, because they require an initial estimate as one of the input variables. Creating a machine learned model requires a list of estimated/actual values, along with any other available information, to build a mapping function.
The sparseness of the data to learn from (at most a few hundred observations of half-a-dozen measured variables, and usually less) has not prevented a stream of puffed-up publications making all kinds of unfounded claims.
Until a few years ago the available public estimation data did not include any information about who made the estimate. Once estimation data contained the information needed to distinguish the different people making estimates, the uncertainty introduced by human variability was revealed (some consistently underestimating, others consistently overestimating, with 25% difference between two estimators being common, and a factor of two difference between some pairs of estimators).
How much accuracy is it realistic to expect with effort estimates?
At the moment we don’t have enough information on the software development process to be able to create a realistic model; without a realistic model of the development process, it’s a waste of time complaining about the availability of information to feed into a model.
I think a project simulation model is the only technique capable of creating a good enough model for use in industry; something like Abdel-Hamid’s tour de force PhD thesis (he also ignores my emails).
We are still in the early stages of finding out the components that need to be fitted together to build a model of software development, e.g., round numbers.
Even if all attempts to build such a model fail, there will be payback from a better understanding of the development process.
No replies to 135 research data requests: paper titles+author emails
I regularly email researchers referring to a paper of theirs I have read, and asking for a copy of the data to use as an example in my evidence-based software engineering book; of course their work is cited as the source.
Around a third of emails don’t receive any reply (a small number ask why they should spend time sorting out the data for me, and I wrote a post to answer this question). If there is no reply after roughly 6-months, I follow up with a reminder, saying that I am still interested in their data (maybe 15% respond). If the data looks really interesting, I might email again after 6-12 months (I have outstanding requests going back to 2013).
I put some effort into checking that a current email address is being used. Sometimes the work was done by somebody who has moved into industry, and if I cannot find what looks like a current address I might email their supervisor.
I have had replies to later email, apologizing, saying that the first email was caught by their spam filter (the number of links in the email template was reduced to make it look less like spam). Sometimes the original email never percolated to the top of their todo list.
There are were originally around 135 unreplied email requests (the data was automatically extracted from my email archive and is not perfect); the list of papers is below (the title is sometimes truncated because of the extraction process).
Given that I have collected around 620 software engineering datasets (there are several ways of counting a dataset), another 135 would make a noticeable difference. I suspect that much of the data is now lost, but even 10 more datasets would be nice to have.
After the following list of titles is a list of the 254 author last known email addresses. If you know any of these people, please ask them to get in touch.
If you are an author of one of these papers: ideally send me the data, otherwise email to tell me the status of the data (I’m summarising responses, so others can get some idea of what to expect).
50 CVEs in 50 Days: Fuzzing Adobe Reader A Change-Aware Per-File Analysis to Compile Configurable Systems A Design Structure Matrix Approach for Measuring Co-Change-Modularity A Foundation for the Accurate Prediction of the Soft Error AGENT-BASED SIMULATION OF THE SOFTWARE DEVELOPMENT PROCESS: A CASE STUDY A Large Scale Evaluation of Automated Unit Test Generation Using A large-scale study of the time required to compromise A Large-Scale Study On Repetitiveness, Containment, and Analysing Humanly Generated Random Number Sequences: A Pattern-Based Analysis of Software Aging in a Web Server Analyzing and predicting effort associated with finding & fixing Analyzing CAD competence with univariate and multivariate Analyzing Differences in Risk Perceptions between Developers Analyzing the Decision Criteria of Software Developers Based on An analysis of the effect of environmental and systems complexity on An Empirical Analysis of Software-as-a-Service Development An Empirical Comparison of Forgetting Models An empirical study of the textual similarity between An error model for pointing based on Fitts' law An Evolutionary Study of Linux Memory Management for Fun and Profit An examination of some software development effort and An Experimental Survey of Energy Management Across the Stack Anomaly Trends for Missions to Mars: Mars Global Surveyor A Quantitative Evaluation of the RAPL Power Control System Are Information Security Professionals Expected Value Maximisers?: A replicated and refined empirical study of the use of friends in A Study of Repetitiveness of Code Changes in Software Evolution A Study on the Interactive Effects among Software Project Duration, Risk Bias in Proportion Judgments: The Cyclical Power Model Capitalization of software development costs Configuration-aware regression testing: an empirical study of sampling Cost-Benefit Analysis of Technical Software Documentation Decomposing the problem-size effect: A comparison of response Determinants of vendor profitability in two contractual regimes: Diagnosing organizational risks in software projects: Early estimation of users’ perception of Software Quality MEASURING USER’S PERCEPTION AND OPINION OF SOFTWARE QUALITY Empirical Analysis of Factors Affecting Confirmation Estimating Agile Software Project Effort: An Empirical Study Estimating computer depreciation using online auction data Estimation fulfillment in software development projects Ethical considerations in internet code reuse: A Evaluating. Heuristics for Planning Effective and Explaining Multisourcing Decisions in Application Outsourcing Exploring defect correlations in a major. Fortran numerical library Extended Comprehensive Study of Association Measures for Eye gaze reveals a fast, parallel extraction of the syntax of Factorial design analysis applied to the performance of Frequent Value Locality and Its Applications Historical and Impact Analysis of API Breaking Changes: How do i know whether to trust a research result? How do OSS projects change in number and size? How much is “about” ? Fuzzy interpretation of approximate Humans have evolved specialized skills of Identifying and Classifying Ambiguity for Regulatory Requirements Identifying Technical Competences of IT Professionals. The Case of Impact of Programming and Application-Specific Knowledge Individual-Level Loss Aversion in Riskless and Risky Choices Industry Shakeouts and Technological Change Inherent Diversity in Replicated Architectures Initial Coin Offerings and Agile Practices Interpreting Gradable Adjectives in Context: Domain Is Branch Coverage a Good Measure of Testing Effectiveness? JavaScript Developer Survey Results Knowledge Acquisition Activity in Software Development Language matters Learning from Evolution History to Predict Future Requirement Changes Learning from Experience in Software Development: Learning from Prior Experience: An Empirical Study of Links Between the Personalities, Views and Attitudes of Software Engineers Making root cause analysis feasible for large code bases: Making-Sense of the Impact and Importance of Outliers in Project Management Aspects of Software Clone Detection and Analysis Managing knowledge sharing in distributed innovation from the Many-Core Compiler Fuzzing Measuring Agility Mining for Computing Jobs Mining the Archive of Formal Proofs. Modeling Readability to Improve Unit Tests Modeling the Occurrence of Defects and Change Modelling and Evaluating Software Project Risks with Quantitative Moore’s Law and the Semiconductor Industry: A Vintage Model Motivations for self-assembling into project teams Networks, social influence and the choice among competing innovations: Nonliteral understanding of number words Nonstationarity and the measurement of psychophysical response in Occupations in Information Technology On information systems project abandonment On the Positive Effect of Reactive Programming on Software ON THE USE OF REPLACEMENT MESSAGES IN API DEPRECATION: On Vendor Preferences for Contract Types in Offshore Software Projects: Peer Review on Open Source Software Projects: Parameter-based refactoring and the relationship with fan-in/fan-out Participation in Open Knowledge Communities and Job-Hopping: Pipeline management for the acquisition of industrial projects Predicting the Reliability of Mass-Market Software in the Marketplace Prototyping A Process Monitoring Experiment Quality vs risk: An investigation of their relationship in Quantitative empirical trends in technical performance Reported project management effort, project size, and contract type. Reproducible Research in the Mathematical Sciences Semantic Versioning versus Breaking Changes Software Aging Analysis of the Linux Operating System Software reliability as a function of user execution patterns Software Start-up failure An exploratory study on the Spatial estimation: a non-Bayesian alternative System Life Expectancy and the Maintenance Effort: Exploring Testing as an Investment The enigma of evaluation: benefits, costs and risks of IT in THE IMPACT OF PLANNING AND OTHER ORGANIZATIONAL FACTORS The impact of size and volatility on IT project performance The Influence of Size and Coverage on Test Suite The Marginal Value of Increased Testing: An Empirical Analysis The nature of the times to flight software failure during space missions Theoretical and Practical Aspects of Programming Contest Ratings The Performance of the N-Fold Requirement Inspection Method The Reaction of Open-Source Projects to New Language Features: The Role of Contracts on Quality and Returns to Quality in Offshore The Stagnating Job Market for Young Scientists Turnover of Information Technology Professionals: Unconventional applications of compiler analysis Unifying DVFS and offlining in mobile multicores Use of Structural Equation Modeling to Empirically Study the Turnover Use Two-Level Rejuvenation to Combat Software Aging and Using Function Points in Agile Projects Using Learning Curves to Mine Student Models Virtual Integration for Improved System Design Which reduces IT turnover intention the most: Workplace characteristics Why Did Your Project Fail? Within-Die Variation-Aware Dynamic-Voltage-Frequency |
Author emails (automatically extracted and manually checked to remove people who have replied on other issues; I hope I have caught them all).
Aaron.Carroll@nicta.com.au abaker@ucar.edu abd_elzamly@yahoo.com actjn@siu.edu agopal@rhsmith.umd.edu akbar.namin@ttu.edu aken@nsuok.edu akmassey@umbc.edu alessandro.murgia@uantwerpen.be alexander.budzier@sbs.ox.ac.uk alinebrito@dcc.ufmg.br Allen.P.Nikora@jpl.nasa.gov Altaf.Ahmad@asu.edu Ana.Aizcorbe@bea.gov angel.garcia@uc3m.es anhnt@iastate.edu a.pinna@diee.unica.it arho.suominen@vtt.fi arie.vandeursen@tudelft.nl asang@ntu.edu.sg awfboh@ntu.edu.sg bent.flyvbjerg@sbs.ox.ac.uk bf@ul.ie bjg@empiricalreality.com bojan.spasic@avl.com bramesh@gsu.edu brent.martin@canterbury.ac.nz briand@simula.no brian.fitzgerald@lero.ie bronevetsky1@llnl.gov burairah@utem.edu.my calikli@chalmers.se canton@mnec.gr cc05@vokac.org celio.santana@gmail.com cguo13@hawk.iit.edu charngda@ccr.buffalo.edu charngdalu@yahoo.com chenyy@comp.nus.edu.sg chris.sauer@sbs.ox.ac.uk christian.korunka@univie.ac.at christopher.lidbury10@imperial.ac.uk clitecky@business.siu.edu cmagee@mit.edu corey.phelps@mcgill.ca cotroneo@unina.it cthompson@cs.berkeley.edu daniela.munteanu@univ-provence.fr daniel.milroy@colorado.edu dan@silverthreadinc.com david@merobe.com david.nembhard@oregonstate.edu der.herr@hofr.at dgrtwo@princeton.edu dhkim@astate.edu director@scit.edu discy@nus.edu.sg djl68@pitt.edu dlautner@hawk.iit.edu dport@hawaii.edu dprtchan@nus.edu.sg dredman@avsi.aero drobinson@stackoverflow.com dskusumo.itt@gmail.com dwheeler@ida.org eherrman@eva.mpg.de Enrique.Dans@ie.edu ermira.daka@sheffield.ac.uk etovar@fi.upm.es fjshull@sei.cmu.edu foreverheart9@gmail.com founders@triplebyte.com fschweitzer@ethz.ch ghs2@psu.edu gleison.brito@dcc.ufmg.br glpkm@hotmail.com gordon.fraser@uni-passau.de greg@bronevetsky.com gul.calikli@gu.se guschroko@student.gu.se hankhoffmann@cs.uchicago.edu hannes.holm@foi.se hata@is.naist.jp hbarth@wesleyan.edu hello@ponyfoo.com hiroshi.igaki@oit.ac.jp hirtle@pitt.edu hoan@iastate.edu hora@dcc.ufmg.br hrideshg@iastate.edu huang@umd.edu huazhe@cs.uchicago.edu hwu28@hawk.iit.edu ichischneider@gmail.com I.Deary@ed.ac.uk ilaria.lunesu@diee.unica.it info@targetprocess.com james@jpallister.com jarmo.ahonen@uef.fi jasmin.blanchette@mpi-inf.mpg.de jasonweiyi@gmail.com javier.alonso@duke.edu jean-luc.autran@univ-provence.fr jfmendes@ua.pt jgo@ua.pt jianh@illinois.edu jimbo@business.siu.edu jmunson@uidaho.edu jo-anne.lefevre@carleton.ca john.krogstie@ntnu.no john.zhang@business.uconn.edu jordan.weissmann@slate.com jose.campos@sheffield.ac.uk josephborel@aol.com jselby@maplesoft.com June.Verner@gmail.com junyang@engr.pitt.edu justinek@alumni.stanford.edu justin.hollands@drdc-rddc.gc.ca j.visser@sig.eu kaisa.still@vtt.fi kantor@cs.technion.ac.il kevin.mcdaid@dkit.ie kewusi@lmu.edu K.Markantonakis@rhul.ac.uk konstantinos.chronis@gmail.com ktrivedi@duke.edu laertexavier@dcc.ufmg.br larissanadja@copin.ufcg.edu.br lcao@odu.edu leo@susaventures.com lionel.briand@uni.lu lsarigia@pme.duth.gr lucia.2009@smu.edu.sg magnus@magnusdettmar.com mail@kaidence.org ma.khan@uleth.ca manuel.oriol@ch.abb.com marc.schulz@rwth-aachen.de Marek@gryting.biz marie-jeanne.lesot@lip6.fr mariusz.musial@ericpol.com maruyama@atr.jp matthias.biggeleben@open-xchange.com matthias.stuermer@iwi.unibe.ch mcknight@bus.msu.edu mdettmar@deloitte.com mdettmar@deloitte.se melanie@cs.columbia.edu Michael.english@lero.ie michael.english@ul.ie michael.grottke@fau.de Michael.Grottke@wiso.uni-erlangen.de Michael@targetprocess.com mingshu@iscas.ac.cn mischael.schill@inf.ethz.ch misof@ksp.sk mjaber@ryerson.ca monica.pais@ifgoiano.edu.br monicaspais@gmail.com mschermann@scu.edu mtov@dcc.ufmg.br mzhu@ets.org ncerpa@utalca.cl Neil.Stewart@warwick.ac.uk Nelson.W.Green@jpl.nasa.gov nick.wells@jobstats.co.uk o.alexy@tum.de oliver.krancher@iwi.unibe.ch Oliver.Laitenberger@horn-company.de olivier.gendreau@polymtl.ca paula.j.savolainen@uef.fi paulmcb@seas.upenn.edu paul@strassmann.com pchatzog@pme.duth.gr perry@mail.utexas.edu philippe.roche@st.com phoonakker@cqpi.engr.wisc.edu pierre.robillard@polymtl.ca ploaiza@lsm.in2p3.fr P.Love@curtin.edu.au pokech@uonbi.ac.ke psidhu@cmu.edu pyzychen@gmail.com ren@iit.edu rh13@aub.edu.lb ricardo.colomo@uc3m.es rkiyer@illinois.edu robert.benkoczi@uleth.ca roberto.natella@unina.it roberto.pietrantuono@unina.it salvaneschi@cs.tu-darmstadt.de saurabh.dighe@intel.com sdorogov@ua.pt sebastien.lefort@lip6.fr sebastien.sauze@l2mp.fr shaji@scit.edu shilin@itechs.iscas.ac.cn show@um.edu.my siegfrie@adelphi.edu simona.ibba@diee.unica.it simon.gaechter@nottingham.ac.uk simonk@rpi.edu simvrh@gmail.com sl@monochromata.de soenke.albers@the-klu.org songxue@microsoft.com s.raemaekers@sig.eu sriram.vangal@intel.com ssg@engr.uconn.edu stavrino@eap.gr stavrino@gmail.com stefan@garage-coding.com sterusso@unina.it steve.a.shogren@gmail.com svkbharathi@scit.edu swilson@tcd.ie tamada@cse.kyoto-su.ac.jp tien@iastate.edu tien.n.nguyen@utdallas.edu tjleffel@gmail.com tkabdelh@nps.edu tsunoda@info.kindai.ac.jp tung@iastate.edu victoria@stodden.net wangyi@us.ibm.com William.L.Taber@jpl.nasa.gov wmhan@takming.edu.tw wobbrock@uw.edu wq@itechs.iscas.ac.cn xenos@eap.gr xhua@hawk.iit.edu xiao.qu@us.abb.com yanglusi@comp.nus.edu.sg ychen200@cba.ua.edu yi.wang@rit.edu yiw@ics.uci.edu yoaval@checkpoint.com zhangx@nku.edu zhij@cs.toronto.edu Zhongju.Zhang@asu.edu zibran@cs.uno.edu |
Update:
Have received a response relating to 6 papers (corresponding paper/author entries in above list deleted).
Algorithms are now commodities
When I first started writing software, developers had to implement most of the algorithms they used; yes, hardware vendors provided libraries, but the culture was one of self-reliance (except for maths functions, which were technical and complicated).
Developers read Donald Knuth’s The Art of Computer Programming, it was the reliable source for step-by-step algorithms. I vividly remember seeing a library copy of one volume, where somebody had carefully hand-written, in very tiny letters, an update to one algorithm, and glued it to the page over the previous text.
Algorithms were important because computers were not yet fast enough to solve common problems at an acceptable rate; developers knew the time taken to execute common instructions and instruction timings were a topic of social chit-chat amongst developers (along with the number of registers available on a given cpu). Memory capacity was often measured in kilobytes, every byte counted.
This was the age of the algorithm.
Open source commoditized algorithms, and computers got a lot faster with memory measured in megabytes and then gigabytes.
When it comes to algorithm implementation, developers are now spoilt for choice; why waste time implementing the ‘low’ level stuff when there were plenty of other problems waiting to be implemented.
Algorithms are now like the bolts in a bridge: very important, but nobody talks about them. Today developers talk about story points, features, business logic, etc. Given a well-defined problem, many are now likely to search for an existing package, rather than write code from scratch (I certainly work this way).
New algorithms are still being invented, and researchers continue to look for improvements to existing algorithms. This is a niche activity.
There are companies where algorithms are not commodities. Google operates on a scale where what appears to others as small improvements, can save the company millions (purely because a small percentage of a huge amount can be a lot). Some company’s core competency may include an algorithmic component (whose non-commodity nature gives the company its edge over the competition), with the non-core competency treating algorithms as a commodity.
Knuth’s The Art of Computer Programming played an important role in making viable algorithms generally available; while the volumes are frequently cited, I suspect they are rarely read (I have not taken any of my three volumes off the shelf, to read, for years).
A few years ago, I suddenly realised that I was working on a book about software engineering that not only did not contain an algorithms chapter, and the 103 uses of the word algorithm all refer to it as a concept.
Today, we are in the age of the ecosystem.
Algorithms have not yet completed their journey to obscurity, which has to wait until people can tell computers what they want and not be concerned about the implementation details (or genetic algorithm programming gets a lot better).
beta: Evidence-based Software Engineering – book
My book, Evidence-based software engineering: based on the publicly available data is now out on beta release (pdf, and code+data). The plan is for a three-month review, with the final version available in the shops in time for Christmas (I plan to get a few hundred printed, and made available on Amazon).
The next few months will be spent responding to reader comments, and adding material from the remaining 20 odd datasets I have waiting to be analysed.
You can either email me with any comments, or add an issue to the book’s Github page.
While the content is very different from my original thoughts, 10-years ago, the original aim of discussing all the publicly available software engineering data has been carried through (in some cases more detailed data, in greater quantity, has supplanted earlier less detailed/smaller datasets).
The aim of only discussing a topic if public data is available, has been slightly bent in places (because I thought data would turn up, and it didn’t, or I wanted to connect two datasets, or I have not yet deleted what has been written).
The outcome of these two aims is that the flow of discussion is very disjoint, even disconnected. Another reason might be that I have not yet figured out how to connect the material in a sensible way. I’m the first person to go through this exercise, so I have no idea where it’s going.
The roughly 620+ datasets is three to four times larger than I thought was publicly available. More data is good news, but required more time to analyse and discuss.
Depending on the quantity of issues raised, updates of the beta release will happen.
As always, if you know of any interesting software engineering data, please tell me.
How should involved if-statement conditionals be structured?
Which of the following two if-statements do you think will be processed by readers in less time, and with fewer errors, when given the value of x, and asked to specify the output?
// First - sequence of subexpressions if (x > 0 && x < 10 || x > 20 && x < 30) print("a"); else print "b"); // Second - nested ifs if (x > 0 && x < 10) print("c"); else if (x > 20 && x < 30) print("d"); else print("e"); |
Ok, the behavior is not identical, in that the else if-arm produces different output than the preceding if-arm.
The paper Syntax, Predicates, Idioms — What Really Affects Code Complexity? analyses the results of an experiment that asked this question, including more deeply nested if-statements, the use of negation, and some for-statement questions (this post only considers the number of conditions/depth of nesting components). A total of 1,583 questions were answered by 220 professional developers, with 415 incorrect answers.
Based on the coefficients of regression models fitted to the results, subjects processed the nested form both faster and with fewer incorrect answers (code+data). As expected performance got slower, and more incorrect answers given, as the number of intervals in the if-condition increased (up to four in this experiment).
I think short-term memory is involved in this difference in performance; or at least I can concoct a theory that involves a capacity limited memory. Comprehending an expression (such as the conditional in an if-statement) requires maintaining information about the various components of the expression in working memory. When the first subexpression of x > 0 && x < 10 || x > 20 && x < 30 is false, and the subexpression after the || is processed, there is no now forget-what-went-before point like there is for the nested if-statements. I think that the single expression form is consuming more working memory than the nested form.
Does the result of this experiment (assuming it is replicated) mean that developers should be recommended to write sequences of conditions (e.g., the first if-statement example) about as:
if (x > 0 && x < 10) print("a"); else if (x > 20 && x < 30) print("a"); else print("b"); |
Duplicating code is not good, because both arms have to be kept in sync; ok, a function could be created, but this is extra effort. As other factors are taken into account, the costs of the nested form start to build up, is the benefit really worth the cost?
Answering this question is likely to need a lot of work, and it would be a more efficient use of resources to address questions about more commonly occurring conditions first.
A commonly occurring use is testing a single range; some of the ways of writing the range test include:
if (x > 0 && x < 10) ... if (0 < x && x < 10) ... if (10 > x && x > 0) ... if (x > 0 && 10 > x) ... |
Does one way of testing the range require less effort for readers to comprehend, and be more likely to be interpreted correctly?
There have been some experiments showing that people are more likely to give correct answers to questions involving information expressed as linear syllogisms, if the extremes are at the start/end of the sequence, such as in the following:
A is better than B
B is better than C |
and not the following (which got the lowest percentage of correct answers):
B is better than C
B is worse than A |
Your author ran an experiment to find out whether developers were more likely to give correct answers for particular forms of range tests in if-conditions.
Out of a total of 844 answers, 40 were answered incorrectly (roughly one per subject; it was a paper and pencil experiment, so no timings). It's good to see that the subjects were so competent, but with so few mistakes made the error bars are very wide, i.e., too few mistakes were made to be able to say that one representation was less mistake-prone than another.
I hope this post has got other researchers interested in understanding developer performance, when processing if-statements, and that they will be running more experiments help shed light on the processes involved.
Recent Comments