Archive
Anthropology and building software systems
Software systems are built by people, who are usually a member of one or more teams. While a lot of research effort has gone into studying the software/hardware used to build these systems, almost no effort has been invested in studying the activities of the people involved.
The study of human behaviors and cultures, in the broadest sense, sits within the field of Anthropology. The traditional image of an Anthropologist is someone who spends an extended period living with some remote tribe, publishing a monograph about their experiences on return to ‘civilisation’. In practice, anthropologists also study local tribes, such as professional workers.
Studies of the computer industry, by anthropologists, include: Global “Body Shopping” An Indian Labor System in the Information Technology Industry by Xiang Biao, and Cultures@SiliconValley by J. A. English-Lueck.
Reporters and professional authors sometimes write popular books for a general audience, which might be labelled pop anthropology. For instance, Kidder’s The Soul of a New Machine.
These academic/reporter publications are usually written by outsiders for an audience of outsiders. They are not intended to provide insights for insiders (Kidder’s book strikes me as reporting on the chaos that ensues when dysfunctional teams have to work together, which is not how it is described on its back cover).
If insiders want to learn about their community, some degree of insider knowledge is needed; exploring culture from the point of view of the subject of the study is known as Ethnography. Acquiring this knowledge can take years, an investment that will deter most researchers. Insightful insider commentary is most likely to come from insiders.
These days, insiders who write usually have blogs. Gerald Weinberg was an insider of times gone by, who wrote popular books for insiders about consulting in the software business; perhaps the most well known being “The Psychology of Computer Programming” (which really ought to be titled “The Sociology of Computer Programming”).
Who might be the consumers of research by anthropologists of software system development (assuming that a non-trivial amount eventually gets done)?
There are important outsiders, such as lawmakers looking to regulate.
Insiders only ever get to experience a sliver of the culture of software communities. The considered experiences of others can provide interesting insights, in particular learning about how teams working within other application domains operate.
Those seeking to change company culture ought to be looking to anthropology as a source of ideas for things that might work, or not.
History deals with the outcomes of past human behavior and culture, and there are a handful of historians of computing.
WebAssembly vs JavaScript performance: 2023 edition
WebAssembly is an assembly-like language intended to be executed by web browsers on an internal stack machine. The intent is that compilers for high-level languages (i.e., C, Cobol, and C#) treat WebAssembly just like they would the assembly language of a cpu. Some substantial applications have been ported, e.g., the R statistical environment, which is written in C and Fortran.
Some people claim that WebAssembly based applications will run faster, and consume less power, than those written in JavaScript or PHP. Now, one virtual machine is as much like any other. Performance differences are driven by compiler optimizations, the ease with which particular language features can be mapped to the available instructions, and an application’s use of easy/hard to map high-level language features.
Researchers have run benchmarks to compare the runtime performance and power consumption of Wasm against other browser based languages, and this post analyses the runtime performance results from two papers.
TL;DR: Relative performance for Wasm/JavaScript varies across browsers and programs. Everything interacts with everything else, which makes analysis complicated.
As is the case with most data analysis in software engineering, the researchers used rudimentary statistical techniques (which is a shame given the huge effort that went into collecting the data). The conclusions of both papers is that for WebAssembly/JavaScript, relative performance issues are complicated, but the techniques they used did not enable them to understand why.
What kind of statistical techniques are applicable for analysing these benchmarks?
Use of different languages/browsers might be expected to have some percentage impact on performance, e.g., programs written in language X will be p% faster/slower. The following equation is one modelling approach, and this equation can be fitted using nonlinear regression:
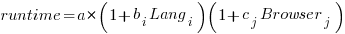, where: 
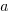is a constant, 
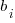is the fitted constant for language 
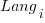, and 
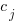is the fitted constant for browser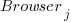 
The problem with this equation is that it involves a separate equation for each combination of language/browser (assuming that all benchmarks are bundled together in the value of 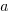). It is possible to use a single equation when there are just two languages/two browsers, by mapping them to the values 0/1.
All languages/browsers/benchmarks can be included in a single linear regression model by treating them as factors in a log transformed model; the equation is: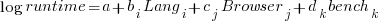 
, where: 
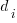is the fitted constant for benchmark 
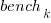. The values of 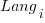, , 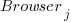and 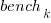are zero, or one for the corresponding fitted constant. All the factors on the right-hand-side are discrete, so a log transform has nothing to distort.
The fitted equation can then be transformed to:
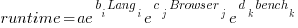
This model assumes that each factor is independent of the others, i.e., the relative performance of each language does not depend on the browser, and that relative performance does not significantly vary between benchmarks, e.g., if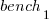 
runs 10% faster when implemented in 
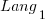, then 
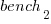also runs close to 10% faster when implemented in .
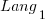How well did the benchmark data from the two papers fit this model, and what were the performance numbers?
The study WebAssembly versus JavaScript: Energy and Runtime Performance by De Macedo, Abreu, Pereira, and Saraiva ran a wide range of benchmarks. It compared C/Wasm/JavaScript running on Chrome/Firefox/Edge. One set of benchmarks were 10 small compute-intensive programs (in Wasm/JavaScript), which were executed with small/medium/large amounts of input data; the other set of benchmarks were two large applications WasmBoy is a Game-boy/Gameboy Color Emulator (written in Typescript and compiled to Wasm), and PSPDFKit supporting viewing, annotating, and filling in forms in PDF documents (written in C/C++ and compiled to a both a subset of JavaScript and Wasm).
Results from the 10 small benchmarks showed strong interactions between browser and language (i.e., Wasm performance relative to JavaScript, varied between browsers; with Edge being faster and Firefox being slower), and a lot of interaction between benchmark and input data size. Support for Wasm is relatively new, relative to the much more mature JavaScript, so it’s not surprising that different browsers have different performance; I’m arm waving when I say that the input size dependency may be related to JIT issues (code).
When interactions are included, the fitted equation has the form:
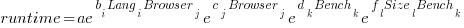
Analysing the results for the two applications, we find that:
- WasmBoy: the factors were independent, and WebAssembly was faster than JavaScript. The
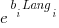factor was 0.84 for Wasm and 1 for JavaScript, - PSPDFKit: there was interaction between the language and browser, with behavior similar to that seen for the small benchmarks.
The study Comparing the Energy Efficiency of WebAssembly and JavaScript in Web Applications on Android Mobile Devices by van Hasselt, Huijzendveld, Noort, de Ruijter, Islam, and Malavolta compared the performance of WebAssembly/JavaScript running compute intensive benchmarks on Firefox/Chrome.
Fitting a regression model to the data from the eight benchmarks showed strong interactions between benchmark programs and language, with each language being faster for some programs (code).
It’s not surprising that the results failed to show a conclusive performance advantage for either WebAssembly or JavaScript, across benchmarks. The situation might change as the wasm virtual machine is tuned, and compilers targetting wasm implement a wider range of optimizations.
Update
A performance analysis of C, Rust, Go, and Javascript compiled to Webassembler
Perturbed expressions may ‘recover’
This week I have been investigating the impact of perturbing the evaluation of random floating-point expressions. In particular, the impact of adding 1 (and larger values) at a random point in an expression containing many binary operators (simply some combination of add/multiply).
What mechanisms make it possible for the evaluation of an expression to be unchanged by a perturbation of +1.0 (and much larger values)? There are two possible mechanisms:
- the evaluated value at the perturbation point is ‘watered down’ by subsequent operations, such that the original perturbed value makes no contribution to the final result. For instance, the IEEE single precision float mantissa is capable of representing 6-significant digits; starting with, say, the value
0.23, perturbing by adding1.0gives1.23, followed by a sequence of many multiplications by values between zero and one could produce, say, the value6.7e-8, which when added to, say,0.45, gives0.45, i.e., the perturbed value is too small to affect the result of the add, - the perturbed branch of the expression evaluation is eventually multiplied by zero (either because the evaluation of the other branch produces zero, or the operand happens to be zero). The exponent of an IEEE single precision float can represent values as small as
1e-38, before underflowing to zero (ignoring subnormals); something that is likely to require many more multiplies than required to lose 6-significant digits.
The impact of a perturbation disappears when its value is involved in a sufficiently long sequence of repeated multiplications.
The probability that the evaluation of a sequence of 
multiplications of random values uniformly distributed between zero and one produces a result less than 
is given by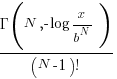 
, where 
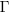is the incomplete gamma function, and 
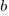is the upper bounds (1 in our case). The plot below shows this cumulative distribution function for various (code):
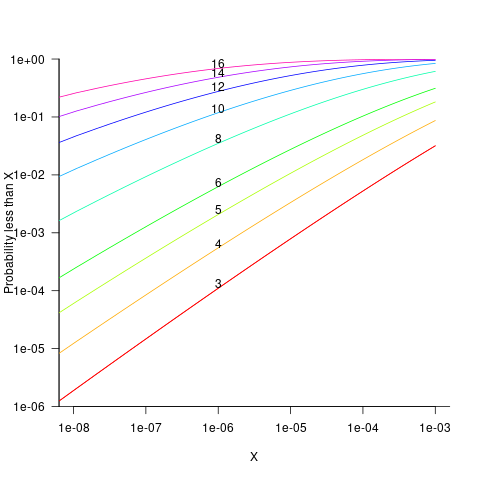
Looking at this plot, a sequence of 10 multiplications has around a 1-in-10 chance of evaluating to a value less than 1e-6.
In practice, the presence of add operations will increase the range of operands values to be greater than one. The expected distribution of result values for expressions containing various percentages of add/multiply operators is covered in an earlier post.
The probability that the evaluation of an expression involves a sequence of multiplications depends on the percentage of multiply operators it contains, and the shape of the expression tree. The average number of binary operator evaluations in a path from leaf to root node in a randomly generated tree of operands is proportional to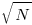 
.
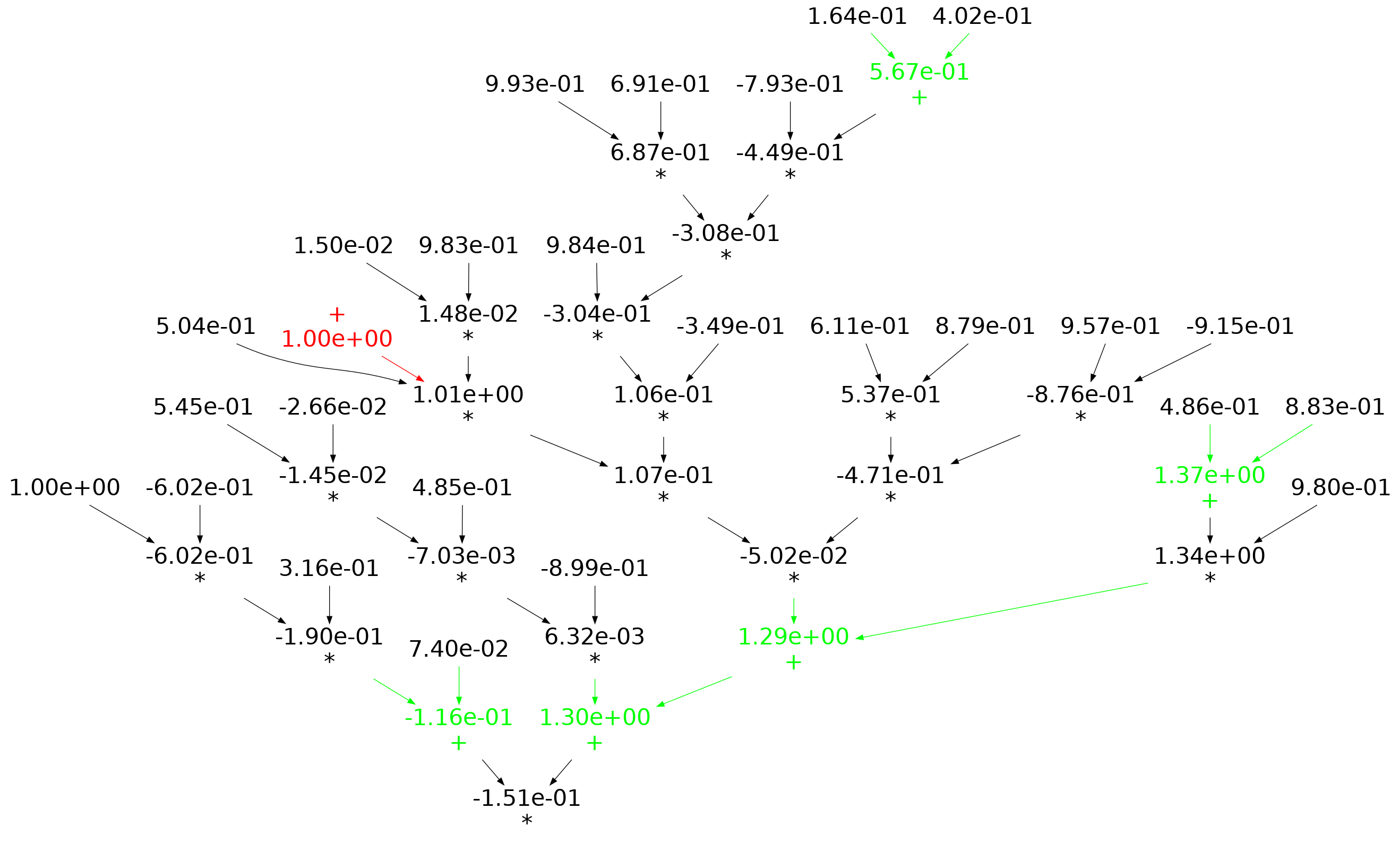
When an expression has a ‘bushy’ balanced form, there are many relatively distinct evaluation paths, the expected number of operations along a path is proportional to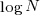 
. The plot below shows a randomly generated ‘bushy’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):
When an expression has a ‘tall’ form, there is one long evaluation path, with a few short paths hanging off it, the expected number of operations along the long path is proportional to . The plot below shows a randomly generated ‘tall’ expression tree containing 25 binary operators, with 80% multiply, and randomly selected values (perturbation in red, additions in green; code+data):
If, one by one, the result of every operator in an expression is systematically perturbed (by adding some value to it), it is known that in some cases the value of the perturbed expression is the same as the original.
The following results were obtained by generating 200 random C expressions containing some percentage of add/multiply, some number of operands (i.e., 25, 50, 75, 100, 150), one-by-one perturbing every operator in every expression, and comparing the perturbed result value to the original value. This process was repeated 200 times, each time randomly selecting operand values from a uniform distribution between -1 and 1. The perturbation values used were: 1e0, 1e2, 1e4, 1e8, 1e16. A 32-bit float type was used throughout.
Depending on the shape of the expression tree, with 80% multiplications and 100 operands, the fraction of perturbed expressions returning an unchanged value can vary from 1% to 40%.
The regression model fitted to the fraction of unchanged expressions contains lots of interactions (the simple version is that the fraction unchanged increases with more multiplications, decreases as the log of the perturbation value, the square root of the number of operands is involved; code+data):
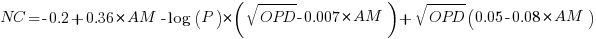
where: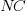 
is the fraction of perturbed expressions returning the original value, 
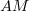the percentage of add operators (not multiply), 
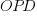the number of operands in the expression, and 
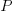the perturbation value.
There is a strong interaction with the shape of the expression tree, but I have not found a way of integrating this into the model.
The following plot shows the fraction of expressions unchanged by adding one, as the perturbation point moves up a tall tree, x-axis, for expressions containing 50 and 100 operands, and various percentages of multiplications (code+data):
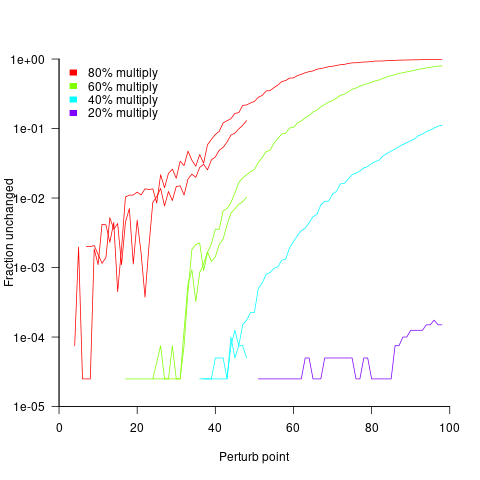
No attempt was made to count the number of expression evaluations where the perturbed value was eventually multiplied by zero (the second bullet point discussed at the start).
Distribution of add/multiply expression values
The implementation of scientific/engineering applications requires evaluating many expressions, and can involve billions of adds and multiplies (divides tend to be much less common).
Input values percolate through an application, as it is executed. What impact does the form of the expressions evaluated have on the shape of the output distribution; in particular: What is the distribution of the result of an expression involving many adds and multiplies?
The number of possible combinations of add/multiply grows rapidly with the number of operands (faster than the rate of growth of the Catalan numbers). For instance, given the four interchangeable variables: w, x, y, z, the following distinct expressions are possible: w+x+y+z, w*x+y+z, w*(x+y)+z, w*(x+y+z), w*x*y+z, w*x*(y+z), w*x*y*z, and w*x+y*z.
Obtaining an analytic solution seems very impractical. Perhaps it’s possible to obtain a good enough idea of the form of the distribution by sampling a subset of calculations, i.e., the output from plugging random values into a large enough sample of possible expressions.
What is needed is a method for generating random expressions containing a given number of operands, along with a random selection of add/multiply binary operators, then to evaluate these expressions with random values assigned to each operand.
The approach I used was to generate C code, and compile it, along with the support code needed for plugging in operand values (code+data).
A simple method of generating postfix expressions is to first generate operations for a stack machine, followed by mapping this to infix form to a postfix form.
The following awk generates code of the form (‘executing’ binary operators, o, right to left): o v o v v. The number of variables in an expression, and number of lines to generate, are given on the command line:
# Build right to left function addvar() { num_vars++ cur_vars++ expr="v " expr # choose variable later } function addoperator() { cur_vars-- expr="o " expr # choose operator later } function genexpr(total_vars) { cur_vars=2 num_vars=2 expr="v v" # Need two variables on stack while (num_vars <= total_vars) { if (cur_vars == 1) # Must push a variable addvar() else if (rand() > 0.2) # Seems to produce reasonable expressions addvar() else addoperator() } while (cur_vars > 1) # Add operators to use up operands addoperator() print expr } BEGIN { # NEXPR and VARS are command line options to awk if (NEXPR != "") num_expr=NEXPR else num_expr=10 for (e=1; e <=num_expr; e++) genexpr(VARS) } |
the following awk code maps each line of previously generated stack machine code to a C expression, wraps them in a function, and defines the appropriate variables.
function eval(tnum) { if ($tnum == "o") { printf("(") tnum=eval(tnum+1) #recurse for lhs if (rand() <= PLUSMUL) # default 0.5 printf("+") else printf("*") tnum=eval(tnum) #recurse for rhs printf(")") } else { tnum++ printf("v[%d]", numvars) numvars++ # C is zero based } return tnum } BEGIN { numexpr=0 print "expr_type R[], v[];" print "void eval_expr()" print "{" } { numvars=0 printf("R[%d] = ", numexpr) numexpr++ # C is zero based eval(1) printf(";\n") next } END { # print "return(NULL)" printf("}\n\n\n") printf("#define NUMVARS %d\n", numvars) printf("#define NUMEXPR %d\n", numexpr) printf("expr_type R[NUMEXPR], v[NUMVARS];\n") } |
The following is an example of a generated expression containing 100 operands (the array v is filled with random values):
R[0] = ((((((((((((((((((((((((((((((((((((((((((((((((( ((((((((((((((((((((((((v[0]*v[1])*v[2])+(v[3]*(((v[4]* v[5])*(v[6]+v[7]))+v[8])))*v[9])+v[10])*v[11])*(v[12]* v[13]))+v[14])+(v[15]*(v[16]*v[17])))*v[18])+v[19])+v[20])* v[21])*v[22])+(v[23]*v[24]))+(v[25]*v[26]))*(v[27]+v[28]))* v[29])*v[30])+(v[31]*v[32]))+v[33])*(v[34]*v[35]))*(((v[36]+ v[37])*v[38])*v[39]))+v[40])*v[41])*v[42])+v[43])+ v[44])*(v[45]*v[46]))*v[47])+v[48])*v[49])+v[50])+(v[51]* v[52]))+v[53])+(v[54]*v[55]))*v[56])*v[57])+v[58])+(v[59]* v[60]))*v[61])+(v[62]+v[63]))*v[64])+(v[65]+v[66]))+v[67])* v[68])*v[69])+v[70])*(v[71]*(v[72]*v[73])))*v[74])+v[75])+ v[76])+v[77])+v[78])+v[79])+v[80])+v[81])+((v[82]*v[83])+ v[84]))*v[85])+v[86])*v[87])+v[88])+v[89])*(v[90]+v[91])) v[92])*v[93])*v[94])+v[95])*v[96])*v[97])+v[98])+v[99])*v[100]); |
The result of each generated expression is collected in an array, i.e., R[0], R[1], R[2], etc.
How many expressions are enough to be a representative sample of the vast number that are possible? I picked 250. My concern was the C compilers code generator (I used gcc); the greater the number of expressions, the greater the chance of encountering a compiler bug.
How many times should each expression be evaluated using a different random selection of operand values? I picked 10,000 because it was a big number that did not slow my iterative trial-and-error tinkering.
The values of the operands were randomly drawn from a uniform distribution between -1 and 1.
What did I learn?
- Varying the number of operands in the expression, from 25 to 200, had little impact on the distribution of calculated values.
- Varying the form of the expression tree, from wide to deep, had little impact on the distribution of calculated values.
- Varying the relative percentage of add/multiply operators had a noticeable impact on the distribution of calculated values. The plot below shows the number of expressions (binned by rounding the absolute value to three digits) having a given value (the power law exponents fitted over the range 0 to 1 are: -0.86, -0.61, -0.36; code+data):
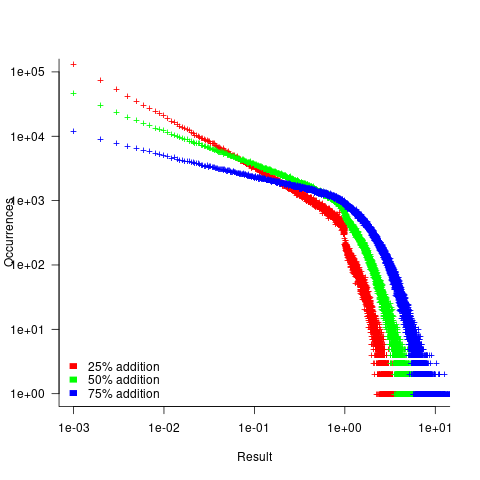
A rationale for the change in the slopes, for expressions containing different percentages of add/multiply, can be found in an earlier post looking at the distribution of many additions (the Irwin-Hall distribution, which tends to a Normal distribution), and many multiplications (integer power of a log).
- The result of many additions is to produce values that increase with the number of additions, and spread out (i.e., increasing variance).
- The result of many multiplications is to produce values that become smaller with the number of multiplications, and become less spread out.
Which recent application spends a huge amount of time adding/multiplying values in the range -1 to 1?
Large language models. Yes, under the hood they are all linear algebra; adding and multiplying large matrices.
LLM expressions are often evaluated using a half-precision floating-point type. In this 16-bit type, the exponent is biased towards supporting very small values, at the expense of larger values not being representable. While operations on a 10-bit significand will experience lots of quantization error, I suspect that the behavior seen above not noticeable change.
Recent Comments