Archive
Statement sequence length for error/non-error paths
One of the folk truisms of the compiler/source code analysis business is that error paths are short, i.e., when an error situation is detected (such as failing to open a file), few statements are executed before the functions returns.
Having repeated this truism for many decades, figure 2 from the paper APEx: Automated Inference of Error Specifications for C APIs jumped off the page at me; thanks to Yuan Kang, I now have a copy of the data.
The plots below (code+data) show two representations of the non-error/error path lengths (measured in statements within individual functions of libc; counting starts at a library call that could return an error value). The upper plot shows statement sequence lengths for error/non-error paths, and the lower is a kernel density plot of the error/non-error sequence lengths.
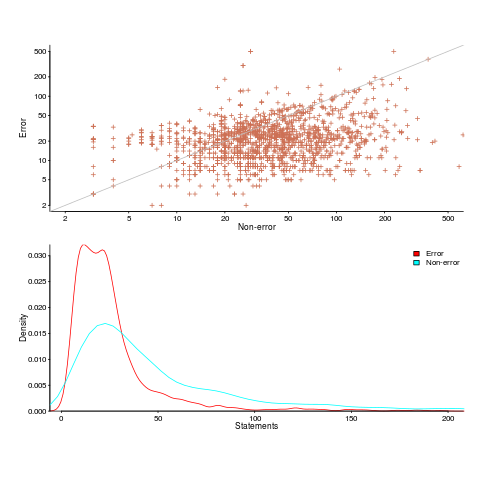
Another truism is that people tend to write positive tests, i.e., tests that do not involve error handling (some evidence).
Code coverage measurements (e.g., number of statements or branches that are executed by a test suite) often show the pattern seen in the plot below (code+data; thanks to the authors of the paper Code Coverage for Suite Evaluation by Developers for making the data available). The data was obtained by measuring the coverage of 1,043 Java programs executing their associated test suite (circles denote program size). Lines are fitted regression models for different sized programs.
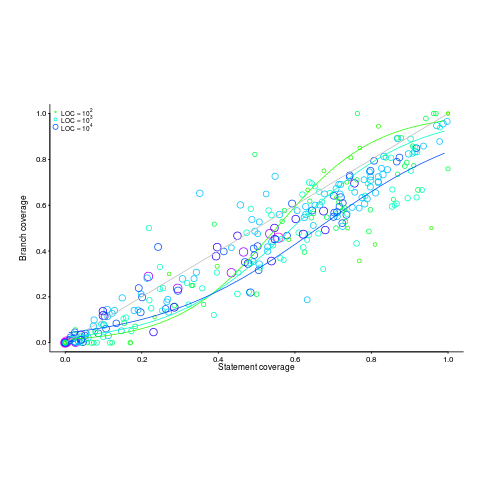
If people are preferentially writing positive tests, test suites with low coverage would be expected to execute a greater percentage of statements than branches (an if-statement has two branches, taken/not-taken), i.e., the behavior seen in the plot above (grey line shows equal statement/branch coverage). Once the low hanging fruit is tested (i.e., the longer, non-error, cases), tests have to be written for the shorter, more likely to be error handling, cases.
The plot would also be explained by typical execution paths favoring longer basic blocks, but I don’t have any data that could show this one way or another.
Mathematical proofs contain faults, just like software
The idea of proving programs correct, like mathematical proofs, is appealing, but is based on an incorrect assumption often made by non-mathematicians, e.g., mathematical proofs are fault free. In practice, mathematicians make mistakes and create proofs that contain serious errors; those of us who are taught mathematical techniques, but are not mathematicians, only get to see the good stuff that has been checked over many years.
An appreciation that published proofs contain mistakes is starting to grow, but Magnificent mistakes in mathematics is an odd choice for a book title on the topic. Quotes from De Millo’s article on “Social Processes and Proofs of Theorems and Programs” now appear regularly; On proof and progress in mathematics is worth a read.
Are there patterns to the faults that appear in claimed mathematical proofs?
- The difficulty of the problem is one obvious issue, as shown by the faulty proofs of the N vs. NP problem,
- the size of the proof, in number of pages, is a common problem, with Mochizuki’s ‘proof’ of the ABC conjecture being a recent example and the Hales-Ferguson proof of the Kepler conjecture has a whole book dedicated to trying to figure out if the proof is correct,
- number of people involved: some of the 100+ mathematicians responsible for proving components of the classification of finite simple groups died before the proof was claimed to be complete; the proofs of the various components created the largest known claimed proof, at tens of thousands of pages.
A surprisingly common approach, used by mathematicians to avoid faults in their proofs, is to state theorems without giving a formal proof (giving an informal one is given instead). There are plenty of mathematicians who don’t think proofs are a big part of mathematics (various papers from the linked-to book are available as pdfs).
Next time you encounter an advocate of proving programs correct using mathematics, ask them what they think about the uncertainty about claimed mathematical proofs and all the mistakes that have been found in published proofs.
Compiler validation is now part of history
Compiler validation makes sense in a world where there are many different hardware platforms, each with their own independent compilers (third parties often implemented compilers for popular platforms, competing against the hardware vendor). A large organization that spends hundreds of millions on a multitude of computer systems (e.g., the U.S. government) wants to keep prices down, which means the cost of porting its software to different platforms needs to be kept down (or at least suppliers need to think it will not cost too much to switch hardware).
A crucial requirement for source code portability is that different compilers be able to compile the same source, generating code that produces the same behavior. The same behavior requirement is an issue when the underlying word-size varies or has different alignment requirements (lots of code relies on data structures following particular patterns of behavior), but management on all sides always seems to think that being able to compile the source is enough. Compilers vendors often supported extensions to the language standard, and developers got to learn they were extensions when porting to a different compiler.
The U.S. government funded a conformance testing service, and paid for compiler validation suites to be written (source code for what were once the Cobol 85, Fortran 78 and SQL validation suites). While it was in business, this conformance testing service was involved C compiler validation, but it did not have to fund any development because commercial test suites were available.
The 1990s was the mass-extinction decade for companies selling non-Intel hardware. The widespread use of Open source compilers, coupled with the disappearance of lots of different cpus (porting compilers to new vendor cpus was always a good money spinner, for the compiler writing cottage industry), meant that many compilers disappeared from the market.
These days, language portability issues have been essentially solved by a near monoculture of compilers and cpus. It’s the libraries that are the primary cause of application portability problems. There is a test suite for POSIX and Linux has its own tests.
There are companies selling compiler C/C++ test suites (e.g., Perennial and PlumHall); when maintaining a compiler, it’s cost-effective to have a set of third-party tests designed to exercise all the language.
The OpenGroup offer to test your C compiler and issue a brand certificate if it passes the tests.
Source code portability requires compilers to have the same behavior and traditionally the generally accepted behavior has been defined by an ISO Standard or how one particular implementation behaved. In an Open source world, behavior is defined by what needs to be done to run the majority of existing code. Does it matter if Open source compilers evolve in a direction that is different from the behavior specified in an ISO Standard? I think not, it makes no difference to the majority of developers; but be careful, saying this can quickly generate a major storm in a tiny teacup.
What instructions should a computer support?
The modern answer to what instructions should a computer support is: lots (e.g., many kinds of: add, subtract, compare, branch, load, store, etc). John von Neumann’s famous First Draft of a Report on the EDVAC, written in 1945, specifies 97 instructions (later, actual implementations contained fewer instructions) and modern Intel processors contain several thousand instructions.
The Turing machine has a very simple instruction set; the machine is driven by a lookup table that specifies one or more of the operations: erase/write a symbol (to the cell currently under the read/write head), move the read/write head left or right (on a tape containing cells), and load a new state (which may be the same as the current one).
When computers were new, the lure of creating a minimalist instruction set had theoretical and practical appeal (valve computers were large and unreliable, reducing the number of components improved reliability and reduced costs).
The design of the IAS machine, built in the late 1940s, was based on von Neumann’s design. Haskell Curry came up with a minimalist set of four instructions that could be used to implement its supported instructions (the idea was that programs would be stored in minimalist form to reduce storage overheads).
Minimalist instruction sets still have theoretical appeal.
Simplicity (rather than minimalism) became fashionable in the 1980s with RISC. This was a reaction to the implementation/runtime costs of very complicated of instructions found in DEC’s VAX and later Motorola’s 68000 processors. Supporting these complicated instructions generated additional overhead for the simpler instructions (which is what most programs spent most of their time executing). The idea behind RISC was that simplifying the instruction set would reduce cpu design costs, improve performance (by making simple instructions fast); leaving the complicated stuff to be supported via software.
Starting out with ‘simple’ MIPS, RISC cpus got successively more complicated with SPARC, Motorola’s MC88000 and then IBM’s RS/6000. I worked on code generators for the SPARC and MC88000 and found them somewhat dull after working on CISC processors. There were huge arguments around RISC vs. CISC (I suspect that many of those involved had never used a RISC processor), but then this was back in the days when many programmers knew a lot of the technical details about the processors they used. (How many of today’s programmers can name the Intel x86 registers?)
More background on 1950s minimalism in the paper: Less is more in the Fifties. Encounters between Logical Minimalism and Computer Design during the 1950s.
These days, people are inventing very different architectures within which existing instructions have to operate, rather than radically new instructions.
Recent Comments