Archive
SEC wants prospectus source code to be published
The US Securities and Exchange Commission are proposing new rules involving the prospectuses for public offerings of asset-backed securities including publishing the source code used to calculate the contractual cash flow provisions.
Requiring that the source code used to perform the financial modeling for a prospectus be made available is an excellent idea. A prospectus document contains a huge number of technical details and more importantly for anybody trying to understand the thinking behind it, a lots of assumption. Writing a program requires that all necessary details be enumerated and appropriately connected together and more importantly creating code that can be meaningfully executed usually means making explicit any assumptions that were previously implicit.
There are parallels here with having access to the source code and data used to make climate predictions.
The authors of the proposals are naive to think that simply requiring source to be written in a language for which there is an open source implementation (i.e., Python) is all they need to specify for others to duplicate the program output generated by the proposer (I have submitted some suggestions to the SEC about the issues that need to be addressed). The suggestions that a formally defined language be used is equally naive.
The availability of this source code opens up some interesting commercial prospects. No, not selling analysis tools to financial institutions but selling them program fault information, e.g., under circumstance X the program incorrectly predicts A will happen when in fact B will actually happen. Of course companies know this will happen and will put a lot more effort into ensuring that their models/code is correct.
Will these disclosure rules change the characteristics of financial software? One characteristic that I’m sure will change is the percentage of swear words in the comments and identifiers.
Brief history of syntax error recovery
Good recovery from syntax errors encountered during compilation is hard to achieve. The two most common strategies are to insert one or more tokens or to delete one or more tokens. Make the wrong decision and a second syntax error will occur, often leading to another and soon the developer is flooded by a nonsensical list of error messages. Compiler writers soon learn that their first priority is ensuring that syntax error recovery does not result in lots of cascading errors. In languages that use a delimiter to indicate end of statement/declaration, usually a semicolon, the error recovery strategy of deleting all tokens until this delimiter is next encountered is remarkably effective.
The era of very good syntax error recovery was the 1970s and early 1980s. Developers working on mainframes might only be able to achieve one or two compilations per day on a batch oriented mainframe and they were not happy if a misplaced comma or space resulted in a whole day being wasted. Most compilers were rented for lots of money and customer demand resulted in some very fancy error recovery strategies.
Borland’s Turbo Pascal had a very different approach to handling errors in code, it stopped processing the source as soon as one was detected. The combination of amazing compilation rates and an interactive environment (MS-DOS running on the machine in front of the developer) made this approach hugely attractive.
To a large extent syntax error recovery has been driven by the methods commonly used to write parsers. Many compilers use a table driven approach to syntax analysis with the tables being generated by parser generator tools such as Yacc. During the 1970s and 80s a lot of the research on parser generators was aimed at reducing the size of the generated tables. A table of 10k bytes was a significant percentage of available storage for machines that supported a maximum of 64k of memory. Some parser table compression techniques involve assuming the default behavior and then handling any special cases when these defaults are found not to apply, but one consequence is that context information needed for good error recovery is often not available when an error is detected. The last major release of Yacc from AT&T in the early 1990s managed another reduction in table size, just as typical storage sizes were getting into the ten of megabytes, but at the expense of increasing the difficulty of doing good error recovery.
While there are still some application areas where the amount of storage occupied by parser tables is still a big issue, e.g., the embedded market, developers of parser generators such as Bison ought to start addressing the needs of users wanting to do good error recovery and who are willing to accept larger tables.
I am pleased to see that the LLVM project is making an effort to provide good syntax error recovery. A frustrating barrier to providing better error recovery is lack of information on the kinds of syntax errors commonly made by developers; there are a few papers and reports containing small scale measurements of errors made by students. Perhaps the LLVM developers will provide a mechanism for automatically collecting compilation errors and providing users with the option to send the results to the LLVM project.
One of my favorite syntax error recovery techniques (implemented in a PL/1 mainframe compiler; I have never been able to justify implementing it on any project I worked on) is the following:
// Use of an undeclared identifier is a syntax error in C and some other // languages, while in other languages it is a semantic error. // no identifier with name result visible here { int result; ... result=... ... } ... calc=result*2; // Error reported by most compilers is use of an undeclared variable |
The ‘real’ error is probably the misplaced closing bracket. Other possibilities include result being a misspelled version of another variable or the assignment to calc being in the wrong place.
There seems to be a trend over the last 20 years to create languages that require more and more semantic information during parsing. Deciphering a syntax error today can involve a lot more than figuring out which surrounding tokens have been omitted or misplaced, information on which types are in scope and visible (oh for the days when that meant the same thing) and where they might be found in the umpteen thousand lines of included source has to be distilled and presented to the developer in a helpful message.
For a long time compilers have primarily been benchmarked on the quality of their code. With every diminishing returns from improved optimization, the increasing complexity of languages and the increasing volume of header code pulled in during compilation perhaps the quality of syntax error recovery will grow in importance.
Number of digits in floating-point literals
Some of the interesting floating-point literals detected by the numbers program not only look uninteresting but plain wrong. For instance, almost every program I analyze appears to contain a literal denoting the ratio of the diameter of the Earth to at least one minor planet. One problem is that most of the numbers contained in the interesting number database are only likely to occur in very specific circumstances and as the size of this database grows the percentage of inappropriate matches grows.
I could (and at some point probably will have to) assign an interestingness level to numbers, but this goes against one of the original aims of identifying the operations performed by unknown source.
An alternative idea is to create a connection between the fuzziness of the matching process and the probability of the literal being encountered in code. For instance, a more exact match might be required for 0.5 because it contains few mantissa digits and sits within a range of values that are commonly encountered, while a much fuzzier match might be used for 1.879623e+3 because it contains more digits and occupies a less commonly encountered range of values.
Floating-point literals often contain leading or trailing zeros, e.g., 0.001, 100.0, 1e+2
or 0.50. Does the presence of these zeros change the probability of a particular mantissa being encountered? For instance the literals 100.0 and 1e+2 have the same numeric value but different numbers of mantissa digits.
Another issue is developer intent. Why did a developer write 0.50, did they simply want two digits to appear after the decimal point because the surrounding literals in the source contain two digits and it makes the visual appearance look better or does this usage denote a quantity whose accuracy is known to two decimal digits?
The following figure is derived from 1 million non-zero floating-point literals contained in ten large, computationally intensive programs.
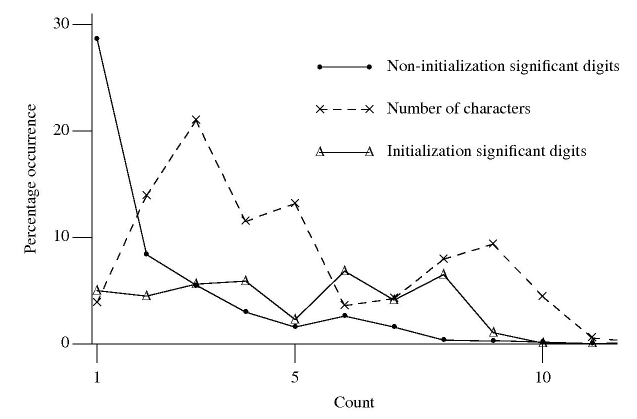
The dashed line denotes the percentage of mantissas containing a given number of characters, including leading/trailing zeros and any decimal point.
The two solid lines denote the digit count of the mantissas with any leading/trailing zeros removed, along with any decimal point, e.g., both 100.0 and 1e+2 would be considered to contain one digit.
It seemed to me that floating-point literals appearing within an initializer attached to a variable definition often contain more digits than literals that appear elsewhere. The solid, triangle tagged, solid line that spends most of its time around 5% are floating-point literals appearing within an initializer (to be exact they are literals separated from another literal by a comma {with some simplistic handling of Fortran line continuation}). The bullet tagged line are all other literals.
I was partially right about the characteristics of floating-point literals in initializers. It turns out the probability of encountering a mantissa containing a given number of digits is approximately constant within an initializer (a more sophisticated analysis might show an upward trend with increasing numbers of digits).
The mantissa digit count outside of initializers has the kind of probability distribution I was looking for. Hopefully this distribution will contribute to a useful measure of interestingness.
What language was an executable originally written in?
Apple have recently added an unusual requirement to the iPhone developer agreement “Applications must be originally written in Objective-C, C, C++, or JavaScript …”. As has been pointed out elsewhere the real purpose is stop third party’s from acquiring any control over application development on Apple’s products; the banning of other languages is presumably regarded as acceptable collateral damage.
Is it possible to tell by analyzing an executable what language it was originally written in?
There are two ways in which executables contain source language ‘signatures’. Detecting these signatures requires knowledge of specific compiler behavior, i.e., a database of information about the behavior of compilers capable of creating the executables is needed.
Runtime library. Most compilers make use of a language specific runtime library, rather than generating inline code for some kinds of functionality. For instance, setjmp/longjmp in C and vtables in C++.
The presence of a known C runtime library does not guarantee that the application was originally written in C; it could have been written in Java and converted to C source.
The absence of a known C runtime library could mean that the source was compiled by a C compiler using a runtime system unknown to the analyzer.
The presence of a known Java, for instance, runtime library would suggest that the original source contained some Java. This kind of analysis would obviously require that the runtime library database not restrict itself to the ‘C’ languages.
Compiler behavior patterns. There is usually more than one way in which a source language construct can be translated to machine code and a compiler has to pick one of them. The perfect optimizing compiler would always make the optimal choice, but real compilers follow a fixed pattern of code generation for at least some language constructs (e.g., initialization of registers on function entry).
The presence of known code patterns in an executable is evidence that a particular compiler has been used; how much depends on the likelihood it could have been generated by other means and how many other patterns suggest the same compiler. In the case of the GNU Compiler Collection the source language might also be Fortran, Java or Ada; I don’t know enough about the behavior of GCC to provide an informed estimate of whether it is possible to recognize the source language from the translated form of constructs shared by several languages, I suspect not.
The fact that an executable can be decompiled to C is not a guarantee that it was originally written in C.
Some languages support source language constructs whose corresponding machine code is unlikely to ever be generated by source from another language. The Fortran computed goto allows constructs to be written that have no equivalent in the other languages supported by GCC (none of them allow statement labels appearing in a multi-way jump to appear before the jump test):
10 I=I+1 20 J=J+1 goto (10, 20, 30, 40) J 30 I=I+3 40 I=I*2 |
The presence of a compiled form of this kind of construct in the executable would be very suggestive of Fortran source.
Apple are famously paranoid and control freakery. It will be very interesting to see what level of compliance checking they decide to perform on executables submitted to the App Store.
On another note: What does “originally written” mean? For instance, many of the mathematical functions (e.g., sine, log, gamma, etc) contained in R were originally written in Fortran and translated to C for use in R; this C source is what is now maintained. Does this historical implementation decision mean that R cannot be legally ported to the iPhone?
Recent Comments