Archive
Techniques used for analyzing basic performance measurements
The statistical design and analysis of experiments is a relatively recent invention (around 150 years old; verifying scientific hypotheses using experiments was first proposed over 1,000 years ago).
Once an experiment has been run, and performance measurements collected, what techniques are available to analyse the data?
Before electronic computers were invented, the practical statistical techniques were those that could be performed manually (perhaps with some help from a mechanical calculator).
Once computers became available, these manual use techniques were widely implemented in statistical applications and libraries. New statistical techniques have been invented that are only of practical when a computer is available, e.g., the bootstrap.
Most researchers in software engineering remain stuck in the pre-computer world of statistical analysis, i.e., failing to use more powerful techniques that make use of computers. Software engineering is not unique in being stuck using pre-computer statistical techniques, there are many other fields that have failed to move on to the more flexible and powerful techniques now available.
Performance comparison by benchmarking (i.e., running an experiment) is a common activity in scientific and engineering fields. Once the measurements have been made, what is the difference between pre-computer and post-manual statistical comparison techniques?
Performance comparison invariably involves comparing the mean/average of each set of measurements (one set for each product benchmarked). Random variations will have some impact on the measured values, and it’s possible that any difference in mean values is the result of these random variations. There are statistical tests for estimating the likelihood of the difference being due to random variation.
Statistical tests invariably come with preconditions on the characteristics of their input data, i.e., the test only works as advertised if the preconditions are met.
The t.test is a popular pre-computer method of estimating the likelihood that the difference between the means of two sets of measurements occurred by chance. Two of its preconditions are that the two sets of input data have a Normal/Gaussian distribution, and have the same standard deviation (if the standard deviations are not equal, Welch’s t-test should be used).
The Mann–Whitney U test (also known as the Wilcoxon rank-sum test) is a pre-computer method with a more relaxed precondition on the distribution of the inputs, requiring only that they are drawn from the same distribution (which need not be a Normal distribution; it is a non-parametric test). This test returns the likelihood of one group being less/greater than the other, and says nothing about the magnitude of the difference.
Removing the constraint that it must be practical to manually perform the calculations, led, in 1979, to a paper proposing the Bootstrap (major issues around the theory underpinning the bootstrap were answered by the early 1990s).
The Bootstrap, a post-manual method, does not have any preconditions on the distribution or standard deviation of the input data. An important precondition is that it is reasonable to assume that the elements of the two sets of measurements are exchangeable (more on this below).
The Bootstrap is a general technique that is not limited to only comparing mean values, it can be used to compare any quantity of interest (assuming the appropriate data is available).
The bootstrap algorithm starts by assuming that, if the two samples are combined into an aggregate sample, all possible permutations of values in this aggregate into two samples are equally likely (this is the exchangeability assumption). If this assumption is true, then any compared difference in the measured two samples will be roughly the same as the compared difference in a pair of random samples drawn from the aggregate.
The computational intensive component of a bootstrap test is generating many pairs of random samples (5,000 is a common choice; sampling with replacement, and saving the result of the comparison).
The comparison results of the paired random samples and the two measured samples are sorted. The position of the measured comparison in this sorted list is the test statistic, i.e., how extreme is the result from the measured samples, compared to the random samples?
News of the flexibility and power of the bootstrap are slowly permeating through the research community. There is an existing way of doing things, and there is little incentive to change. As Plank famously observed: “Science advances one funeral at a time.”
What impact might my evidence-based book have in 2021?
What impact might the release of my evidence-based software engineering book have on software engineering in 2021?
Lots of people have seen the book. The release triggered a quarter of a million downloads, or rather it getting linked to on Twitter and Hacker News resulted in this quantity of downloads. Looking at the some of the comments on Hacker News, I suspect that many ‘readers’ did not progress much further than looking at the cover. Some have scanned through it expecting to find answers to a question that interests them, but all they found was disconnected results from a scattering of studies, i.e., the current state of the field.
The evidence that source code has a short and lonely existence is a gift to those seeking to save time/money by employing a quick and dirty approach to software development. Yes, there are some applications where a quick and dirty iterative approach is not a good idea (iterative as in, if we make enough money there will be a version 2), the software controlling aircraft landing wheels being an obvious example (if the wheels don’t deploy, telling the pilot to fly to another airport to see if they work there is not really an option).
There will be a few researchers who pick up an idea from something in the book, and run with it; I have had a couple of emails along this line, mostly from just starting out PhD students. It would be naive to think that lots of researchers will make any significant changes to their existing views on software engineering. Planck was correct to say that science advances one funeral at a time.
I’m hoping that the book will produce a significant improvement in the primitive statistical techniques currently used by many software researchers. At the moment some form of Wilcoxon test, invented in 1945, is the level of statistical sophistication wielded in most software engineering papers (that do any data analysis).
Software engineering research has the feeling of being a disjoint collection of results, and I’m hoping that a few people will be interested in starting to join the dots, i.e., making connections between findings from different studies. There are likely to be a limited number of major dot joinings, and so only a few dedicated people are needed to make it happen. Why hasn’t this happened yet? I think that many academics in computing departments are lifestyle researchers, moving from one project to the next, enjoying the lifestyle, with little interest in any research results once the grant money runs out (apart from trying to get others to cite it). Why do I think this? I have emailed many researchers information about the patterns I have found in the data they sent me, and a common response is almost completely disinterest (some were interested) in any connections to other work.
What impact do you think ‘all’ the evidence presented will have?
Data analysis with a manual mindset
A lot of software engineering data continues to be analysed using techniques designed for manual implementation (i.e., executed without a computer). Yes, these days computers are being used to do the calculation, but they are being used to replicate the manual steps.
Statistical techniques are often available that are more powerful than the ‘manual’ techniques. They were not used during the manual-era because they are too computationally expensive to be done manually, or had not been invented yet; the bootstrap springs to mind.
What is the advantage of these needs-a-computer techniques?
The main advantage is not requiring that the data have a Normal distribution. While data having a Normal, or normal-like, distribution is common is the social sciences (a big consumer of statistical analysis), it is less common in software engineering. Software engineering data is often skewed (at least the data I have analysed) and what appear to be outliers are common.
It seems like every empirical paper I read uses a Mann-Whitney test or Wilcoxon signed-rank test to compare two samples, sometimes preceded by a statement that the data is close to being Normal, more often being silent on this topic, and occasionally putting some effort into showing the data is Normal or removing outliers to bring it closer to being Normally distributed.
Why not use a bootstrap technique and not have to bother about what distribution the data has?
I’m not sure whether the reason is lack of knowledge about the bootstrap or lack of confidence in not following the herd (i.e., what will everybody say if my paper does not use the techniques that everybody else uses?)
If you are living on a desert island and don’t have a computer, then you will want to use the manual techniques. But then you probably won’t be interested in analyzing software engineering data.
Quality of data analysis: two recent papers
Software engineering research has and continues to suffer from very low quality data analysis. The underlying problem is that practitioners are happy to go along with the status quo, not bothering to learn basic statistics or criticize data analysis in papers they are asked to review. Two recent papers I have read spring out as being at opposite ends of the spectrum.
In their paper A replicated survey of IT software project failures Khaled El Emam and A. Günes Koru don’t just list the mean values for the responses they get they also give the 95% confidence bounds on those values. At a superficial level this has the effect of making their results look much less interesting; for instance a quick glance at Table 3 “Reasons for project cancellation” suggests there is a significant difference between “Lack of necessary technical skills” at 22% and “Over schedule” at 17% but a look at the 95% confidence bounds, (6%–48%) and (4%–41%) respectively, shows that almost nothing can be said about the relative contribution of these two reasons (why publish these numbers, because nothing else has been published and somebody has to start somewhere). The authors understand the consequences of using a small sample size and have the integrity to list the confidence bounds rather than leave the reader to draw completely unjustified conclusions. I wish everybody was as careful and upfront about their analysis as these authors.
The paper Assessing Programming Language Impact on Development and Maintenance: A Study on C and C++ by Pamela Bhattacharya and Iulian Neamtiu takes some interesting ideas and measurements and completely mangles the statistical analysis (something the conference’s reviewers should have picked up on).
I encourage everybody to measure code and do statistical analysis. It looks like what happened here is that a PhD student got in over her head and made lots of mistakes, something that happens to us all when learning a new subject. The problem is that these mistakes made it through into a published paper and its conclusions are likely to repeated (these conclusions may or may not be true and it may or may not be possible to reliably test them from the data gathered, but the analysis presented in the paper faulty and so its conclusions cannot be trusted). I hope the authors will reanalyze their data using the appropriate techniques and publish an updated version of the paper.
Some of the hypothesis being tested include:
- C++ is replacing C as a main development language. The actual hypothesis tested is the more interesting question: “Is the percentage of C++ in projects that also contain substantial amounts of C growing at the expense of C?”
So the unit of measurement is the project and only four of these are included in the study; an extremely small sample size that must have an error bound of around 50% (no mention of error bounds in the paper). The analysis of the data claims to use linear regression but seems completely confused, lets not get bogged down in the details but move on to other more obvious mistakes.
- C++ code is of higher internal quality than C code. The data consists of various source code metrics, ignoring whether these are a meaningful measure of quality, lets look at how the numbers are analysed. I was somewhat surprised to read: “the distributions of complexity values … are skewed, thus arithmetic mean is not the right indicator of an ongoing trend. Therefore, …, we use the geometric mean …” While the arithmetic mean might not be a useful indicator (I have trouble seeing why not), use of the geometric mean is bizarre and completely wrong. Because of its multiplicative nature the geometric mean of a set of values having a fixed arithmetic mean decreases as its variance increases. For instance, the two sets of values (40, 60) and (20, 80) both have an arithmetic mean of 50, while their geometric means are 48.98979 (i.e.,
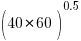) and 40 (i.e., 
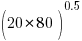) respectively.
So if anything can be said about the bizarre idea of comparing the geometric mean of complexity metrics as they change over time, it is that increases/decreases are an indicator of decrease/increase in variance of the measurements.
- C++ code is less prone to bugs than C code. The statistical analysis here made a common novice mistake. The null hypothesis tested was: “C code has lower or equal defect density than C++ code.” and this was rejected. The incorrect conclusion drawn was that “C++ code is less prone to bugs than C code.” Statistically one does not follow from the other, the data could be inconclusive and the researchers should have tested this question as the null hypothesis if this is the claim they wanted to make. There are also lots of question marks over other parts of the analysis, but this is the biggest blunder.
Recent Comments