Archive
An experiment involving matching regular expressions
Recommendations for/against particular programming constructs have one thing in common: there is no evidence backing up any of the recommendations. Running experiments to measure the impact of particular language features on developer performance is not something that researchers do (there have been a handful of experiments looking at the impact of strong typing on developer performance; the effect measured was tiny).
In February I discovered two groups researching regular expressions. In the first post on duplicate regexs, I promised to say something about the second group. This post discusses an experiment comparing developer comprehension of various regular expressions; the paper is: Exploring Regular Expression Comprehension.
The experiment involved 180 workers on Mechanical Turk (to be accepted, workers had to correctly answer four or five questions about regular expressions). Workers/subjects performed two different tasks, matching and composition.
- In the matching task workers saw a regex and a list of five strings, and had to specify whether the regex matched (or not) each string (there was also an unsure response).
- In the composition task workers saw a regular expression, and had to create a string matched by this regex. Each worker saw 10 different regexs, which were randomly drawn from a set of 60 regexs (which had been created to be representative of various regex characteristics). I have not analysed this data yet.
What were the results?
For the matching task: given each of the pairs of regexs below, which one (of each pair) would you say workers were most likely to get correct?
R1 R2 1. tri[a-f]3 tri[abcdef]3 2. no[w-z]5 no[wxyz]5 3. no[w-z]5 no(w|x|y|z)5 4. [ˆ0-9] [\D] |
The percentages correct for (1) were essentially the same, at 94.0 and 93.2 respectively. The percentages for (2) were 93.3 and 87.2, which is odd given that the regex is essentially the same as (1). Is this amount of variability in subject response to be expected? Is the difference caused by letters being much less common in text, so people have had less practice using them (sounds a bit far-fetched, but its all I could think of). The percentages for (3) are virtually identical, at 93.3 and 93.7.
The percentages for (4) were 58 and 73.3, which surprised me. But then I have been using regexs since before \D support was generally available. The MTurk generation have it easy not having to use the ‘hard stuff’ 😉
See Table III in the paper for more results.
This matching data might be analysed using Item Response theory, which can take into account differences in question difficulty and worker/subject ability. The plot below looks complicated, but only because there are so many lines. Each numbered colored line is a different regex, worker ability is on the x-axis (greater ability on the right), and the y-axis is the probability of giving a correct answer (code+data; thanks to Peipei Wang for fixing the bugs in my code):
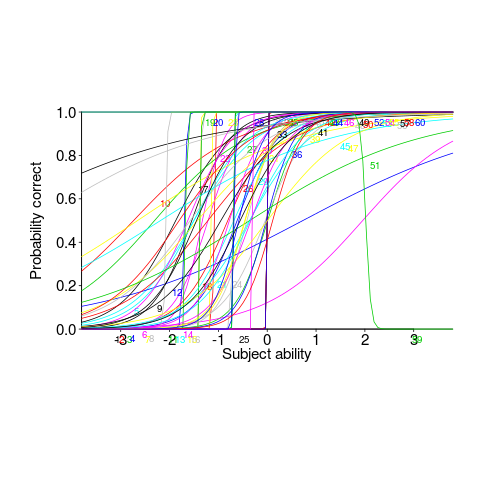
Yes, for question 51 the probability of a correct answer decreases with worker ability. Heads are being scratched about this.
There might be some patterns buried in amongst all those lines, e.g., particular kinds of patterns require a given level of ability to handle, or correct response to some patterns varying over the whole range of abilities. These are research questions, and this is a blog article: answers in the comments 🙂
This is the first experiment of its kind, so it is bound to throw up more questions than answers. Are more incorrect responses given for longer regexs, particularly if they cannot be completely held in short-term memory? It is convenient for the author to use a short-hand for a range of characters (e.g., a-f), and I was expecting a difference in performance when all the letters were enumerated (e.g., abcdef); I had theories for either one being less error-prone (I obviously need to get out more).
Patterns of regular expression usage: duplicate regexs
Regular expressions are widely used, but until recently they were rarely studied empirically (i.e., just theory research).
This week I discovered two groups studying regular expression usage in source code. The VTSBULeeLab has various papers analysing 500K distinct regular expressions, from programs written in eight languages and StackOverflow; Carl Chapman and Peipei Wang have been looking at testing of regular expressions, and also ran an interesting experiment (I will write about this when I have decoded the data).
Regular expressions are interesting, in that their use is likely to be purely driven by an application requirement; the use of an integer literals may be driven by internal housekeeping requirements. The number of times the same regular expression appears in source code provides an insight (I claim) into the number of times different programs are having to solve the same application problem.
The data made available by the VTSBULeeLab group provides lots of information about each distinct regular expression, but not a count of occurrences in source. My email request for count data received a reply from James Davis within the hour 🙂
The plot below (code+data; crates.io has not been included because the number of regexs extracted is much smaller than the other repos) shows the number of unique patterns (y-axis) against the number of identical occurrences of each unique pattern (x-axis), e.g., far left shows number of distinct patterns that occurred once, then the number of distinct patterns that each occur twice, etc; colors show the repositories (language) from which the source was obtained (to extract the regexs), and lines are fitted regression models of the form: 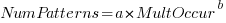 , where:
, where: 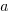 is driven by the total amount of source processed and the frequency of occurrence of regexs in source, and
is driven by the total amount of source processed and the frequency of occurrence of regexs in source, and 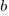 is the rate at which duplicates occur.
is the rate at which duplicates occur.
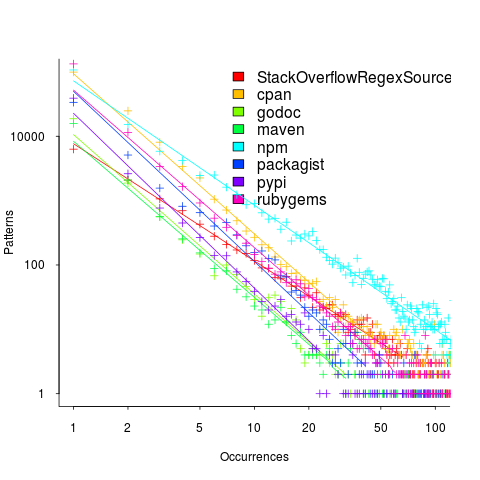
So most patterns occur once, and a few patterns occur lots of times (there is a long tail off to the unplotted right).
The following table shows values of 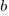 for the various repositories (languages):
for the various repositories (languages):
StackOverflow cpan godoc maven npm packagist pypi rubygems
-1.8 -2.5 -2.5 -2.4 -1.9 -2.6 -2.7 -2.4 |
The lower (i.e., closer to zero) the value of 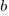 , the more often the same regex will appear.
, the more often the same regex will appear.
The values are in the region of -2.5, with two exceptions; why might StackOverflow and npm be different? I can imagine lots of duplicates on StackOverflow, but npm (I’m not really familiar with this package ecosystem).
I am pleased to see such good regression fits, and close power law exponents (I would have been happy with an exponential fit, or any other equation; I am interested in a consistent pattern across languages, not the pattern itself).
Some of the code is likely to be cloned, i.e., cut-and-pasted from a function in another package/program. Copy rates as high as 70% have been found. In this case, I don’t think cloned code matters. If a particular regex is needed, what difference does it make whether the code was cloned or written from scratch?
If the same regex appears in source because of the same application requirement, the number of reuses should be correlated across languages (unless different languages are being used to solve different kinds of problems). The plot below shows the correlation between number of occurrences of distinct regexs, for each pair of languages (or rather repos for particular languages; top left is StackOverflow).

Why is there a mix of strong and weakly correlated pairs? Is it because similar application problems tend to be solved using different languages? Or perhaps there are different habits for cut-and-pasted source for developers using different repositories (which will cause some patterns to occur more often, but not others, and have an impact on correlation but not the regression fit).
There are a lot of other interesting things that can be done with this data, when connected to the results of the analysis of distinct regexs, but these look like hard work, and I have a book to finish.
Matching context sensitive rules and generating output using regular expressions
I have previously written about generating words that sound like an input word. My interest in reimplementing this project from many years ago was fueled by a desire to find out exactly how flexible modern regular expression libraries are (the original used a bespoke tool). I had a set of regular expressions describing a mapping from one or more letters to one or more phonemes and I wanted to use someone else’s library to do all the heavy duty matching.
The following lists some of the mapping rules. The letters between [] are the ones that are ‘consumed’ by the match and any letters/characters either side are the context required for the rule to match. The characters between // are phonemes represented using the Arpabet phonetic transcription.
@[ew]=/UW/ [giv]=/G IH V/ [g]i^=/G/ [ge]t=/G EH/ su[gges]=/G JH EH S/ [gg]=/G/ b$[g]=/G/ [g]+=/JH/ # space - start of word # $ - one or more vowels # ! - two or more vowels # + - one front vowel # : - zero or more consonants # ^ - one consonant # ; - one or more consonants # . - one voiced consonant # @ - one special consonant # & - one sibilant # % - one suffix |
After some searching I settled on using the PCRE (Perl Compatible Regular Expressions) library, which contains more functionality than you can shake a stick at.
My plan was to translate each of the 300+ rules, using awk, into a regular expression, concatenate all of these together using alternation and let PCRE handle all of the matching details; which is what I did and it worked. Along the way a few problems had to be solved…
How can the appropriate phoneme(s) be generated when a rule matches? The solution is to use what PCRE calls callouts. During matching if the sequence (?C77) is encountered in the pattern a developer defined function (set up prior to calling pcre_execute) is called with information about the current state of the match. In this example the information would include the value 77 (values between 0 and 255 are supported). By embedding a unique number in the subpattern for each rule (and writing the appropriate phoneme sequence out to a configuration file that is read on program startup) it is possible to generate the appropriate output (because there are more than 255 rules a pair of callouts are needed to specify larger values).
How can the left/right letter context be handled? Most regular expression matching works by consuming all of the matched characters, making them unavailable for matching by other parts of the regular expression during that match. PCRE supports what it calls left and right assertions, which require a pattern to match but don’t consume the matched characters, leaving them to be matched by some other part of the pattern. So the rule [ge]t is mapped to the regular expression ge(?=t) which consumes a ge followed by a t but leaves the t for matching by another part of the pattern.
One problem occurs for backward assertions, which are restricted to matching the same number of characters for all alternatives of the pattern. For example the backward assertion (?<=(a|ab)e) is not supported because one path through the pattern is two characters long while the other is three characters long. The rule @[ew] cannot be matched using a backward assertion because @ includes letter sequences of different length (e.g., N, J, TH). The solution is to use a callout to perform a special left context match (specified by the callout number) which works by reversing the word being matched and the left context pattern and performing a forward (rather than backward) match.
The final pattern is over 10,000 characters long and looks something like (notice that everything is enclosed in () and terminated by a + to force the longest possible match, i.e., the complete word:
(((a(?=$)(?C51)))|((?<=^)(are(?=$)(?C52)))| ... |(z(?C106)(?C55)))+ |
Now we need a method of using the letter to phoneme rules to map phonemes to letters. In some cases a phoneme sequence can be mapped to multiple letter sequences and I wanted to generate all of the possible letter sequences (e.g., cat -> K AE T -> cat, kat, qat). PCRE does support a matching function capable of returning all possible matches. However this function does not support some of the functionality required, so I decided to 'force' the single match function to generate all possible sequences by using a callout to make it unconditionally fail as the last operation of every otherwise successful match, causing the matching process to backtrack and try to find an alternative match. Not the most efficient of solutions but it saved me having to learn a lot more about the functionality supported by PCRE.
For a given sequence of phonemes it is simple enough to match it using a regular expression created from the existing rules. However, any match also needs to meet any left/right letter context requirements. Because we are generating letters left to right we have a left context that can be matched, but no right context.
The left context is matched by applying the technique used for variable length left contexts, described above, i.e., the letters generated so far are reversed and these are matched using a reversed left context pattern.
An efficient solution to matching right context would be very fiddly to implement. I took the simple approach of ignoring the right letter context until the complete phoneme sequence had been matched; the generated letter sequence out of this matching process is feed as input to the letter-to-phoneme function and the returned phoneme sequence compared against the original generating phoneme sequence. If the two phoneme sequences are identical the generated letter sequence is included in the final set of returned letter sequences. Not very computer efficient, but an efficient use of my time.
I could not resist including some optimzations. For instance, if a letter sequence only matches at the start or end of a word then the corresponding phonemes can only match at the start/end of the sequence.
I have skipped some of the minor details, which you can read about in the source of the tool.
I would be interested to hear about the libraries/tools used by readers with experience matching patterns of this complexity.
Relative spacing of operands affects perception of operator precedence
What I found most intriguing about Google Code Search (shutdown Nov 2011) was how quickly searches involving regular expressions returned matches. A few days ago Russ Cox, the implementor of Code Search not only explained how it worked but also released the source and some precompiled binaries. Google’s database of source code did not include the source of R, so I decided to install CodeSearch on my local machine and run some of my previous searches against the latest (v2.14.1) R source.
In 2007 I ran an experiment that showed developers made use of variable names when making binary operator precedence decisions. At about the same time two cognitive psychologists, David Landy and Robert Goldstone, were investigating the impact of spacing on operator precedence decisions (they found that readers showed a tendency to pair together the operands that were visibly closer to each other, e.g., a with b in a+b * c rather than b with c).
As somebody very interested in finding faults in code the psychologists research findings on spacing immediately suggested to me the possibility that ‘incorrectly’ spaced expressions were a sign of failure to write code that had the intended behavior. Feeding some rather complicated regular expressions into Google’s CodeSearch threw up a number of ‘incorrectly’ spaced expressions. However, this finding went no further than an interesting email exchange with Landy and Goldstone.
Time to find out whether there are any ‘incorrectly’ spaced expressions in the R source. cindex (the tool that builds the database used by csearch) took 3 seconds on a not very fast machine to process all of the R source (56M byte) and build the search database (10M byte; the Linux database is a factor of 5.5 smaller than the sources).
The search:
csearch "w(+|-)w +(*|/) +w" |
returned a few interesting matches:
... modules/internet/nanohttp.c: used += tv_save.tv_sec + 1e-6 * tv_save.tv_usec; modules/lapack/dlapack0.f: $ ( T*( ONE+SQRT( ONE+S / T ) ) ) ) modules/lapack/dlapack2.f: S = Z( 3 )*( Z( 2 ) / ( T*( ONE+SQRT( ONE+S / T ) ) ) ) modules/lapack/dlapack4.f: $ ( T*( ONE+SQRT( ONE+S / T ) ) ) ) |
There were around 15 matches of code like 1e-6 * var (because the pattern w is for alphanumeric sequences and that is not a superset of the syntax of floating-point literals).
The subexpression ONE+S / T is just the sort of thing I was looking for. The three instances all involved code that processed tridiagonal matrices in various special cases. Google search combined with my knowledge of numerical analysis was not up to the task of figuring out whether the intended usage was (ONE+S)/T or ONE+(S/T).
Searches based on various other combination of operator pairs failed to match anything that looked suspicious.
There was an order of magnitude performance difference for csearch vs. grep -R -e (real 0m0.167s vs. real 0m2.208s). A very worthwhile improvement when searching much larger code bases with more complicated patterns.
Recent Comments