Archive
Superoptimizers are back in vogue
There has always been the need for a few developers with in-depth knowledge of a particular cpu architecture to sit down and think very hard about how best to implement a snippet of code performing some operation in assembly language, e.g., library implementors wanting the tightest code for a critical inner loop or compiler writers who need to map from intermediate code to machine code.
In 1987 Massalin published his now famous paper that introduced the term Superoptimizer; a program that enumerates all possible combinations of instruction sequences until the shortest/fastest one producing the desired output from the given input is found (various heuristics were used to prune the search space e.g., only considering 15 or so opcodes, and the longest sequence it ever generated contained 12 instructions).
While the idea was widely talked about, it never caught on in practice (a special purpose branch eliminator was produced for GCC; Hacker’s Delight also includes a stand-alone system). Perhaps the guild of mindbogglingly-obtuse-but-fast-instruction-sequences black-balled it (apprentices have to spend several years doing nothing but writing assembly code for their chosen architecture, thinking about how to make it go faster and/or be shorter and only talk to other apprentices/members and communicate with non-converts exclusively about their latest neat sequence), or perhaps it was just a case of not invented here (writing machine code used to be something that even run-of-the-mill developers got to do every now and again), or perhaps it was not considered cost-effective to build a superoptimizer for a given project (I don’t know of anyone offering a generic tool that could be tailored for specific cases) or perhaps developers were happy to just ride the wave of continually faster processors.
It was not until 2008 with Bansal’s thesis that superoptimizer research started to take off (as in paper publication rate increased from once every five years to more than one a year). Bansal found a new market, binary translation i.e., translating the binary of a program built to run on one kind of cpu to run on a different kind of cpu, for instance the Mac 68K emulator.
Bansal and other researchers’ work was oriented towards relatively short instruction sequences. To be really useful, some way of handling longer sequences was needed.
A few days ago Stochastic Superoptimization arrived on the scene (or rather a paper describing it became available for download). Schkufza, Sharma and Aiken use Markov chain Monte Carlo methods to sample the possible instruction sequences rather than generating all of them. The paper gives a 116 instruction example from which the author’s tool removed 16 lines to produce code that went 1.6 times faster (only 30 ‘core’ instructions were given in paper); what is also very interesting is that the tool operates on compiler generated output (gcc/llvm), suggesting the usage build program, profile it and then stochastic superoptimize the hot spots.
Markov chains and Monte Carlo methods are trendy topics that researchers like to write about, so we will certainly see more papers in this area.
These days few developers have had hands-on experience with machine code, so the depth of expertise that was once easy to find is now rare, processors have many more weird and wonderful instructions often interacting with older instructions in obscure ways, and the cpu architecture landscape continues to change regularly. The time may have arrived for superoptimizers to be widely used by industry.
Of course, superoptimizers can work at any level of abstraction, including expression trees built directly from some complicated floating-point calculation that needs to be optimized for accuracy or speed.
Why does Coverity restrict who can see its tool output?
Coverity generate a lot of publicity from their contract (started under a contract with the US Department of Homeland Security, don’t know if things have changed) to scan large quantities of open source software with their static analysis tools and a while back I decided to have a look at the warning messages they produce. I was surprised to find that access to the output required singing a non-disclosure agreement, this has subsequently been changed to agreeing to a click-through license for the basic features and signing a NDA for access to advanced features. Were Coverity limiting access because they did not want competitors learning about new suspicious constructs to flag, or because they did not want potential customers seeing what a poor job their tool did?
The claim that access “… for most projects is permitted only to members of the scanned project, partially in order to ensure that potential security issues may be resolved before the public sees them.” does not really hold much water. Anybody interested in finding security problems in code could probably find hacked versions of various commercial static analysis tools to download. The SAMATE – Software Assurance Metrics And Tool Evaluation project runs yearly evaluations of static analysis tools and makes the results publicly available.
A recent blog post by Andy Chou, Coverity’s CTO, added weight to the argument that their Scan tool is rather run-of-the-mill. The post discussed a new check that had recently been added flagging occurrences of memcmp, and related standard library functions, that were being tested for equality (or inequality) with specific integer constants (these functions are defined to return a negative or positive value or 0, and while many implementations always return the negative value -1 and the positive value 1 a developer should always test for the property of being negative/positive and not specific values that have that property). Standards define library functions to have a wide variety of different properties, and tools that check for correct application of these properties have been available for over 15 years.
My experience of developer response, when told that some library function is required to return a negative value and some implementation might not return -1, is that they regard any implementation not returning -1 as being ‘faulty’ since all implementations in their experience return -1. I imagine that library implementors are aware of this expectation and try to meet it. However, optimizing compilers often try to automatically inline calls to memcpy and related copy/compare functions and will want to take advantage of the freedom to return any negative/positive value if it means not having to perform a branch test (a big performance killer on most modern processors).
An academic programming language paper about R
The R language has passed another milestone, a paper aimed at the academic programming language community (or at least one section of this community) has been written about it, Evaluating the Design of the R Language by Morandat, Hill, Osvald and Vitek. Hardly earth shattering news, but it may have some impact on how R is viewed by nonusers of the language (the many R users in finance probably don’t care that R seems to have been labeled as the language for doing statistics). The paper is well written and contains some very interesting information as well as a few mistakes, although it will probably read like gobbledygook to anybody not familiar with academic programming language research. What follows has something of the form of an R users guide to reading this paper, plus some commentary.
The paper has roughly three parts, the first gives an overview of R, the second is a formal definition of a subset and the third an initial report of an analysis of R usage. For me and I imagine you dear reader the really interesting stuff is in the third section.
When giving a language overview to people who know other computer languages it makes sense to leverage that knowledge, this is why the discussion has a world view from the perspective of languages rarely associated with R: Scheme, Haskell and CLOS. I found some of the discussion of R constructs to be much more informative and less confusing than that in nearly all R books/tutorials I have read, but then they are written from a detailed operational programming language perspective. One criticism of this overview is that it does not give any hint as to why R has such a large following (saying that users found it more useful than these languages would send the wrong kind of signal ;-).
What is a formal description of a subset of R (i.e., done purely using mathematics) doing in the second part? Well, until recently very little academic software engineering was empirically based and was populated by people I would classify as failed mathematicians without the common sense needed to be engineers. Things are starting to change but research that measures things, particularly people, is still regarded as not being respectable in some quarters. In this case the formal definition is playing the role of a virility symbol showing that the authors are obviously regular guys who happen to be indulging in a bit of empirical research.
A surprising number of papers measuring the usage of real software contain formal definitions of a subset of the language being measured. Subsets are used because handling the complete language is a big project that usually involves one or more people getting a PhD out of the work. The subset chosen have to look plausible to readers who understand the mathematics but not the programming language, broadly handle all the major constructs but not get involved with all the fiddly details that need years of work and many pages to describe.
The third part contains the real research, which is really about one implementation of R and the characteristics of R source in the CRAN and Bioconductor repositories, and contains lots of interesting information. Note: the authors are incorrect to aim nearly all of the criticisms in this subsection at R, these really apply to the current implementation of R and might not apply to a different implementation.
In a previous post I suggested some possibilities for speeding up the execution of R programs that depended on R usage characteristics. The Morandat paper goes a long way towards providing numbers for some of these usage characteristics (e.g., 37% of function parameters are assigned to and 36% of vectors contain a single value).
What do we learn from this first batch of measurements? R users rarely use many of the more complicated features (e.g., object oriented constructs {and this paper has been accepted at the European Conference on Object-Oriented Programming}), a result usually seen for other languages. I was a bit surprised that R programs were only 40% smaller than equivalent C programs. I think part of the reason is that some of the problems used for benchmarking are not the kind that would usually be solved using R and I did not see any ‘typical’ R programs being coded up in C for comparison, another possibility is that the authors were not thinking in R when writing the code.
One big measurement topic the authors missed is comparing their general findings with usage measurements of other languages. I think they will find lots of similar patterns of usage.
The complaint that R has been defined by the successive releases of its only implementation, rather than a written specification, applies to all widely used languages, at least in their early days. Back in the day a major reason for creating language standards for Pascal and then C was so that other implementations could be created; the handful of major languages whose specification was written before the first implementation (e.g., PL/1, Ada) have/are dieing out. Are multiple implementations needed in an Open Source world? The answer seems to be no for Perl and yes for PHP, Ruby etc. The effort needed to create a written specification for the R language might be better invested improving the efficiency of the current implementation so that a better alternative is not needed.
Needless to say the authors suggested committing the fatal programming language research mistake.
The authors have created an interesting set of tools for static and dynamic analysis of R and I look forward to reading more about their findings in future papers.
Estimating the reliability of compiler subcomponent
Compiler stress testing can be used for more than finding bugs in compilers, it can also be used to obtain information about the reliability of individual components of a compiler. A recent blog post by John Regehr, lead investigator for the Csmith project, covered a proposal to improve an often overlooked aspect of automated compiler stress testing (removing non-essential code from a failing test case so it is small enough to be acceptable in a bug report; attaching 500 lines of source to a report in a sure fire way for it to be ignored) triggered this post. I hope that John’s proposal is funded and it would be great if the researchers involved also received funding to investigate component reliability using the data they obtain.
One process for estimating the reliability of the components of a compiler, or any other program, is:
- divide the compiler into a set of subcomponents. These components might be a collection of source files obtained through cluster analysis of the source, obtained from a functional analysis of the implementation documents or some other means,
- count the number of times each component executes correctly and incorrectly (this requires associating bugs with components by tracing bug fixes to the changes they induce in source files; obtaining this information will consume the largest amount of the human powered work) while processing lots of source. The ratio of these two numbers, for a given component, is an estimate of the reliability of that component.
How important is one component to the overall reliability of the whole compiler? This question can be answered if the set of components is treated as a Markov chain and the component transition probabilities are obtained using runtime profiling (see Large Empirical Case Study of Architecture–based Software Reliability by Goševa-Popstojanova, Hamill and Perugupalli for a detailed discussion).
Reliability is a important factor in developers’ willingness to enable some optimizations. Information from a component reliability analysis could be used to support an option that only enabled optimization components having a reliability greater than a developer supplied value.
The one big threat to validity of this approach is that stress tests are not representative of typical code. One possibility is to profile the compiler processing lots of source (say of the order of a common Linux distribution) and merge the transition probabilities, probably weighted, to those obtained from stress tests.
Compiler benchmarking for the 21st century
I would like to propose a new way of measuring the quality of a compiler’s code generator: The highest quality compiler is one that generates identical code for all programs that produce the same output, e.g., a compiler might spot programs that calculate pi and always generate code that uses the most rapidly converging method known. This is a very different approach to the traditional methods based on using (mostly) execution time or size (usually code but sometimes data) as a measure of quality.
Why is a new measurement method needed, and why choose this one? It is relatively easy for compiler vendors to tune their products to the commonly used benchmark and they seem to have lost their role as drivers for new optimization techniques. Different developers have different writing habits and companies should not have to waste time and money changing developer habits just to get the best quality code out of a compiler; compilers should handle differences in developer coding habits and not let it affect the quality of generated code. There are major savings to be had by optimizing the effect that developers are trying to achieve rather than what they have actually written (these days new optimizations targeting at what developers have written show very low percentage improvements).
Deducing that a function calculates pi requires a level of sophistication in whole program analysis that is unlikely to be available in production compilers for some years to come (ok, detecting 4*atan(1.0) is possible today). What is needed is a collection of compilable files containing source code that aims to achieve an outcome in lots of different ways. To get the ball rolling the “3n times 2” problem is presented as the first of this new breed of benchmarks.
The “3n times 2” problem is a variant on the 3n+1 problem that has been tweaked to create more optimization opportunities. One implementation of the “3n times 2” problem is:
if (is_odd(n)) n = 3*n+1; else n = 2*n; // this is n = n / 2; in the 3n+1 problem |
There are lots of ways of writing code that has the same effect, some of the statements I have seen for calculating n=3*n+1 include: n = n + n + n + 1, n = (n << 1) + n + 1 and n *= 3; n++, while some of the ways of checking if n is odd include: n & 1, (n / 2)*2 != n and n % 2.
I have created a list of different ways in which 3*n+1 might be calculated and is_odd(n) might be tested and written a script to generate a function containing all possible permutations (to reduce the number of combinations no variants were created for the least interesting case of n=2*n, which was always generated in this form). The following is a snippet of the generated code (download everything):
if (n & 1) n=(n << 2) - n +1; else n*=2; if (n & 1) n=3*n+1; else n*=2; if (n & 1) n += 2*n +1; else n*=2; if ((n / 2)*2 != n) { t=(n << 1); n=t+n+1; } else n*=2; if ((n / 2)*2 != n) { n*=3; n++; } else n*=2; |
Benchmarks need a means of summarizing the results and here I make a stab at doing that for gcc 4.6.1 and llvm 2.9, when executed using the -O3 option (output here and here). Both compilers generated a total of four different sequences for the 27 'different' statements (I'm not sure what to do about the inline function tests and have ignored them here) with none of the sequences being shared between compilers. The following lists the number of occurrences of each sequence, e.g., gcc generated one sequence 16 times, another 8 times and so on:
gcc 16 8 2 1 llvm 12 6 6 3
How might we turn these counts into a single number that enables compiler performance to be compared? One possibility is to award 1 point for each of the most common sequence, 1/2 point for each of the second most common, 1/4 for the third and so on. Using this scheme, gcc gets 20.625, and llvm gets 16.875. So gcc has greater consistency (I am loathed to use the much overused phrase higher quality).
Now for a closer look at the code generated.
Both compilers always generated code to test the least significant bit for the conditional expressions n & 1 and n % 2. For the test (n / 2)*2 != n gcc generated the not very clever right-shift/left-shift/compare while llvm and'ed out the bottom bit and then compared; so both compilers failed to handle what is a surprisingly common check for a number being odd.
The optimal code for n=3*n+1 on a modern x86 processor is (lots of register combinations are possible, let's assume rdx contains n) leal 1(%rdx,%rdx,2), %edx and this is what both compilers generated a lot of the time. This locally optimal code is not always generated because:
- gcc fails to detect that
(n << 2)-n+1is equivalent to(n << 1)+n+1and generates the sequenceleal 0(,%rax,4), %edx ; subl %eax, %edx ; addl $1, %edx(I pointed this out to a gcc maintainer sometime ago, and he suggested reporting it as a bug). This 'bug' occurs three times in total. - For some forms of the calculation llvm generates globally better code by taking the else arm into consideration. For instance, when the calculation is written as
n += (n << 1) +1llvm deduces that(n << 1)and the2*nin theelseare equivalent, evaluates this value into a register before performing the conditional test thus removing the need for an unconditional jump around the 'else' code:leal (%rax,%rax), %ecx testb $1, %al je .LBB0_8 # BB#7: orl $1, %ecx # deduced ecx is even, arithmetic unit not needed! addl %eax, %ecx .LBB0_8:
This more efficient sequence occurs nine times in total.
The most optimal sequence was generated by gcc:
testb $1, %dl leal (%rdx,%rdx), %eax je .L6 leal 1(%rdx,%rdx,2), %eax .L6: |
with llvm and pre 4.6 versions of gcc generating the more traditional form (above, gcc 4.6.1 assumes that the 'then' arm is the most likely to be executed and trades off a leal against a very slow jmp):
testb $1, %al je .LBB0_5 # BB#4: leal 1(%rax,%rax,2), %eax jmp .LBB0_6 .LBB0_5: addl %eax, %eax .LBB0_6: |
There is still room for improvement, perhaps by using the conditional move instruction (which gcc actually generates within the not-very-clever code sequence for (n / 2)*2 != n) or by using the fact that eax already holds 2*n (the potential saving would come through a reduction in complexity of the internal resources needed to execute the instruction).
llvm insists on storing the calculated value back into n at the end of every statement. I'm not sure if this is a bug or a feature designed to make runtime debugging easier (if so it ought to be switched off by default).
Missed optimization opportunities (not intended to be part of this benchmark and if encountered would require a restructuring of the test source) include noticing that if  is odd then
is odd then 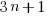 is always even, creating the opportunity to perform the following multiply by 2 without an if test.
is always even, creating the opportunity to perform the following multiply by 2 without an if test.
Perhaps one day, compilers will figure out when a program is calculating pi and generate code that uses the best known algorithm. In the meantime, I am interested in hearing suggestions for additional different-algorithm-same-code benchmarks.
Fibonacci and JIT compilers
To maximize a compiler’s ability to generate high quality code many programming language standards do not specify the order in which the operands of a binary operator are evaluated. Most of the time the order of operand evaluation does not matter because all orders produce same final result. For instance in x + y the value of x may be obtained followed by obtaining the value of y and the two values added, alternatively the value of y may be obtained first followed by obtaining the value of x and the two values added; optimizers make use of local context information (e.g., holding one of the values in a register so it is immediately available for use in the evaluation of multiple instances of x) to work out which order produces the highest quality code.
If one of the operands is a function call that modifies the value of the other operand the result may depend on the order of evaluation. For instance, in:
int x; int set_x(void) { x=1; return 1; } int two_values(void) { x=0; return x + set_x(); } |
a left to right evaluation order of the return expression in two_values produces the value 1, while a right to left evaluation order produces the value 2. Every now and again developers accidentally write code that does something like this and are surprised to see program behavior change when they use different compiler options, a new version of the compiler or a different compiler (all things that can result in the order of evaluation changing for a given expression).
It is generally assumed that two calls to two_values within the same program will always produce the same answer, i.e., the decision on which order of evaluation to use is made at compile time and never changes while a program is running. Neither the C++ or C Standard requires that the evaluation order be fixed prior to program execution and use of a just-in-time compiler could result in the value returned by two_values alternating between 1 and 2. Some languages (e.g., Java) for which JIT compilers are expected to be used specify the exact order in which operands have to be evaluated.
One possible way of finding out whether a JIT compiler is being used for your C/C++ program is to test the values returned by two calls to two_values. A JIT compiler may, but is not required, to return different values on each call. Of course a decide-prior-to-execution C/C++ compiler does have the option of optimizing the following function to return true or false on the basis that the standard permits this behavior, but I would be very surprised to see this occur in practice:
bool Schrödinger(void) { return two_values() == two_values(); } |
The runtime variability offered by JIT compilers makes it possible to write a program whose output can be any value between 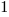 and
and 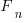 (the
(the  ‘th Fibonacci number, where
‘th Fibonacci number, where n is read from the input):
#include <stdio.h> int x; int set_x(int ret_val) { x=1; return ret_val; } int two_unspec(void) { x=0; return x + set_x(1); } int add_zero(val) { x=0; return val - x + set_x(0); } int fib(int fib_num) { if (fib_num > 3) return fib(fib_num-2) + add_zero(fib(fib_num-1)); else if (fib_num == 3) return two_unspec(); else return 1; } int main(void) { int n; scanf("%d", &n); printf("Fibonacci %d = %d\n", n, filb(n)); } |
The C-semantics tool will ‘execute’ this program and produce a list of the 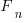 possible outputs (a PhD project under active development; the upper limit is currently around the 6th Fibonacci number which requires 11 hours and produces a 50G log file).
possible outputs (a PhD project under active development; the upper limit is currently around the 6th Fibonacci number which requires 11 hours and produces a 50G log file).
A decide-prior-to-execution compiler has a maximum choice of four possible outputs for a given input value and for a given executable the output produced by different input values will be perfectly correlated.
Why does Intel sell compilers?
Intel is a commercial company and the obvious answer to the question of why it sells compilers is: to make money. Does a company that makes billions of dollars in profits really have any interest in making a few million, I’m guessing, from selling compilers? Of course not, Intel’s interest in compilers is as a means of helping them sell more hardware.
How can a compiler be used to increase computer hardware sales? One possibility is improved performance and another is customer perception of improved performance. My company’s first product was a code optimizer and I was always surprised by the number of customers who bought the product without ever performing any before/after timing benchmarks; I learned that engineers are seduced by the image of performance and only a few are ever forced to get involved in measuring it (having been backed into a corner because what they currently have is not good enough).
Intel are not the only company selling x86 chips, AMD and VIA have their own Intel compatible x86 chips. Intel compatible? Doesn’t that mean that programs compiled using the Intel compiler will execute just as quickly on the equivalent chip sold by competitors? Technically the answer is no, but the performance differences are likely to be small in most cases. However, I’m sure there are many developers who have been seduced by Intel’s marketing machine into believing that they need to purchase x86 chips from Intel to make sure they receive this ‘worthwhile’ benefit.
Where do manufacturer performance differences, for the same sequence of instructions, come from? They are caused by the often substantial internal architectural difference between the processors sold by different manufacturers, also Intel and its competitors are continually introducing new processor architectures and processors from the same company will have differences performance characteristics. It is possible for an optimizer to make use of information on different processor characteristics to tune the machine code generated for a particular high-level language construct, with the developer selecting the desired optimization target processor via compiler switches.
Optimizing code for one particular processor architecture is a specialist market. But let’s not forget all those customers who will be seduced by the image of performance and ignore details such as their programs being executed on a wide variety of architectures.
The quality of a compiler’s runtime library can have a significant impact on a program’s performance. The x86 instruction set has grown over time and large performance gains can be had by a library function that adapts to the instructions available on the processor it is currently executing on. The CPUID instruction provides all of the necessary information.
As well as providing information on the kind of processor and its architectural features the CPUID instruction can return information about the claimed manufacturer of the chip (some manufacturers provide a mechanism that allows users to change the character sequence returned by this instruction).
The behavior of some of the functions in Intel’s runtime library depends on the
character sequence returned by the CPUID instruction, producing better performance for the sequence “GenuineIntel”. The US Federal Trade Commission have filed a complaint alleging that this is anti-competitive (more details) and requested that this manufacturer dependency be removed.
I think that removing this manufacturer dependency will have little impact on sales. Any Intel compiler user who is not targeting Intel chips and who is has a real interest in performance can patch the runtime library, the Supercomputer crowd will want to talk to the kind of sophisticated processor/compiler engineers that Intel makes available and for everybody else it is about the perception of performance. In fact Intel ought to agree to a ‘manufacturer free’ runtime library pronto before too many developers have their delusions shattered.
Assuming compilers are clever enough (part 1)
Developers often assume the compiler they use will do all sorts of fancy stuff for them. Is this because they are lazy and happy to push responsibility for parts of the code they write on to the compiler, or do they actually believe that their compiler does all the clever stuff they assume?
An example of unmet assumptions about compiler performance is the use of const in C/C++, final in Java or readonly in other languages. These are often viewed as a checking mechanism, i.e., the developer wants the compiler to check that no attempt is made to, accidentally, change the value of some variable, perhaps via code added during maintenance.
The surprising thing about variables in source code is that approximately 50% of them don’t change once they have been assigned a value (A Theory of Type Qualifiers for C measurements and Automatic Inference of Stationary Fields for Java).
Developers don’t use const/final qualifiers nearly as often as they could. Most modern compilers can deduce if a locally defined variable is only assigned a value once and make use of this fact during optimization. It takes a lot more resources to deduce this information for non-local variables; developers want their compiler to be fast and so implementors don’t won’t them waiting around while whole program analysis is performed.
Why don’t developers make more use of const/final qualifiers? Is this usage, or lack of, an indicator that developers don’t have an accurate grasp of variable usage, or that they don’t see the benefit of using these qualifiers or perhaps they pass responsibility on to the compiler (program size seems to grow sufficiently fast that whole program optimization often consumes more memory than likely to be available; and when are motherboards going to break out of the 4G limit?)
Code generation via machine learning
Commercial compiler implementors have to produce compilers that are capable of being used on a typical developer computer. A whole bunch of optimization techniques were known for years but could not be used because few computers had the available memory capacity (in the days when 2M was a lot of memory your author once attended a talk that presented some impressive results and was frustrated to learn that the typical memory footprint was 160M, who would ever imagine developers having so much memory to work within?) These days the available of gigabytes of storage has means that likely computer storage capacity is rarely a reason not to use some optimization technique, although the whole program optimization people are still out in the cold.
What is new these days is the general availability of multiple processors. The obvious use of multiple processors is to have make distribute the compilation load. The more interesting use is having the compiler apply different sets of optimizations techniques on different processors, picking the one that produces the highest quality code.
Optimizing code generation algorithms don’t appear to leave anything to chance and individually they generally don’t. However, selecting an order in which to apply individual optimization algorithms is something of a black art. In some cases code transformations made by one algorithm can interfere with the performance of another algorithm. In some cases the possibility of the interference is known and applies in one direction, choosing the appropriate relative ordering of the two algorithms solves the problem. In other cases the way in which two algorithms interfere with each other depends on the code being translated, now the ordering of the two algorithms becomes problematic. The obvious solution is to try both orderings and pick the one that produces the best result.
Several research groups have investigated the use of machine learning in compiler optimization. cTuning.org is a new project that aims to bring together groups interested in self-tuning adaptive computing systems based on statistical and machine learning techniques.
Commercial pressure is always forcing compiler implementors to produce faster code and use of machine learning techniques can produce some impressive results. Now that multi-processor systems are common it will not be long before compilers writers start to make use of the extra resources now available to them.
The safety critical people have problems trying to show the correctness of compiler output that has been generated by ‘fixed’ algorithms. It is not hard to envisage that in 10 years time all large production quality compilers will be using machine learning.
Recent Comments