Archive
Procedure nesting a once common idiom
Structured programming was a popular program design methodology that many developers/managers claimed to be using in the 1970s and 1980s. Like all popular methodologies, everybody had/has their own idea about what it involves, and as always, consultancies sprang up to promote their take on things. The 1972 book Structured programming provides a taste of the times.
The idea underpinning structured programming is that it’s possible to map real world problems to some hierarchical structure, such as in the image below. This hierarchy model also provided a comforting metaphor for those seeking to understand software and its development.

The disadvantages of the Structured programming approach (i.e., real world problems often have important connections that cannot be implemented using a hierarchy) become very apparent as programs get larger. However, in the 1970s the installed memory capacity of most computers was measured in kilobytes, and a program containing 25K lines of code was considered large (because it was enough to consume a large percentage of the memory available). A major program usually involved running multiple, smaller, programs in sequence, each reading the output from the previous program. It was not until the mid-1980s…
At the coding level, doing structured programming involves laying out source code to give it a visible structure. Code blocks are indented to show if/for/while nesting and where possible procedure/functions are nested within the calling procedures (before C became widespread, functions that did not return a value were called procedures; Fortran has always called them subroutines).
Extensive nesting of procedures/functions was once very common, at least in languages that supported it, e.g., Algol 60 and Pascal, but not Fortran or Cobol. The spread of C, and then C++ and later Java, which did not support nesting (supported by gcc as an extension, nested classes are available in C++/Java, and later via lambda functions), erased nesting from coding consideration. I started life coding mostly in Fortran, moved to Pascal and made extensive use of nesting, then had to use C and not being able to nest functions took some getting used to. Even when using languages that support nesting (e.g., Python), I have not reestablished by previous habit of using nesting.
A common rationale for not supporting nested functions/methods is that it complicate the language specification and its implementation. A rather self-centered language designer point of view.
The following Pascal example illustrates a benefit of being able to nest procedures/functions:
procedure p1; var db :array[db_size] of char; procedure p2(offset :integer); function p3 :integer; begin (* ... *) return db[offset]; end; begin var off_val :char; off_val=p3; (* ... *) end; begin (* ... *) p2(3) end; |
The benefit of using nesting is in not forcing the developer to have to either define db at global scope, or pass it as an argument along the call chain. Nesting procedures is also a method of information hiding, a topic that took off in the 1970s.
To what extent did Algol/Pascal developers use nested procedures? A 1979 report by G. Benyon-Tinker and M. M. Lehman contains the only data I am aware of. The authors analysed the evolution of procedure usage within a banking application, from 1973 to 1978. The Algol 60 source grew from 35,845 to 63,843 LOC (657 procedures to 967 procedures). A large application for the time, but a small dataset by today’s standards.
The plot below shows the number of procedures/functions having a particular lexical nesting level, with nesting level 1 is the outermost level (i.e., globally visible procedures), and distinct colors denoting successive releases (code+data):
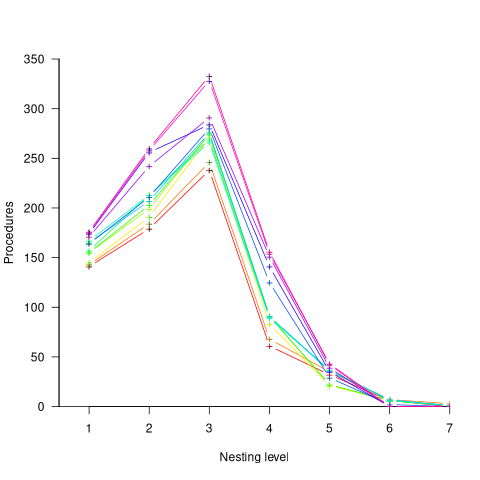
Just over 78% of procedures are nested within at least one other procedure. It’s tempting to think that nesting has a Poisson distribution, however, the distribution peaks at three rather than two. Perhaps it’s possible to fit an over-dispersed, but this feels like creating a just-so story.
What is the distribution of nested functions/methods in more recently written source? A study of 35 Python projects found 6.5% of functions nested and over twice as many (14.2%) of classed nested.
Are there worthwhile benefits to using nested functions/methods where possible, or is this once common usage mostly fashion driven with occasional benefits?
Like most questions involving cost/benefit analysis of language usage, it’s probably not sufficiently interesting for somebody to invest the effort required to run a reliable study.
if statement conditions, some basic measurements
The conditions contained in if-statements control all the decisions a program makes, yet relatively little is known about their characteristics.
A condition contains one or more clauses, for instance, the condition (a && b) contains two clauses that both need to be true, for the condition to be true. An earlier post modelled the number of clauses in Java conditions, and found an exponential decline (around 90% of conditions contained a single clause, for C this is around 85%).
The condition in a nested if-statement contains implicit decisions, because its evaluation depends on the conditions evaluated by its outer if-statements. I have long predicted that, on average, the number of clauses in a condition will decrease as if-statement nesting increases, because some decisions are subsumed by outer conditions. I have not seen any measurements on conditionals vs nesting, and this week this question reached the top of my to-do list.
I used Coccinelle to extract the text contained in each condition, along with the start/end line numbers of the associated if/else compound statement(s). After almost 20 years, Coccinelle is still the most flexible C source analysis tool available that does not require delving into compiler internals. The following is an example of the output (code and data):
file;stmt;if_line;if_col;cmpd_end;cmpd_line_end;expr sqlite-src-3460100/src/fkey.c;if;240;10;240;243;aiCol sqlite-src-3460100/src/fkey.c;if;217;6;217;217;! zKey sqlite-src-3460100/src/fkey.c;if;275;8;275;275;i == nCol sqlite-src-3460100/src/fkey.c;if;1428;6;1428;1433;aChange == 0 || fkParentIsModified ( pTab , pFKey , aChange , bChngRowid ) sqlite-src-3460100/src/fkey.c;if;808;4;808;808;iChildKey == pTab -> iPKey && bChngRowid sqlite-src-3460100/src/fkey.c;if;452;4;452;454;nIncr > 0 && pFKey -> isDeferred == 0 |
The conditional expressions (last column above) were reduced to a basic form involving simple variables and logical operators, along with operator counts. Some example output below (code and data):
simp_expr,land,lor,ternary v1,0,0,0 v1 && v2,1,0,0 v1 || v2,0,1,0 v1 && v2 && v3,2,0,0 v1 || ( v2 && v3 ),1,1,0 ( v1 && v2 ) || ( v3 && v4 ),2,1,0 ( v1 ? dm1 : dm2 ),0,0,1 |
The C source code projects measured were the latest stable versions of Vim (44,205 if-statements), SQLite (27,556 if-statements), and the Linux kernel (version 6.11.1; 1,446,872 if-statements).
A side note: I was surprised to see the ternary operator appearing in some conditions; in effect, an if within an if (see last line of the previous example). The ternary operator usually appears as a component of a large conditional expression (e.g., x + ( v1 ? dm1 : dm2 ) > y), rather than itself containing clauses, e.g., ( v1 ? dm1 : dm2 ) && v2. I have not seen the requirements for this operator discussed in any analysis of MC/DC.
The plot below shows the number of if-statements occurring at a given nesting level, along with regression fits, of the form 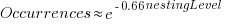 , to the Vim and SQLite data; the Linux data was better fit by a power law (code+data):
, to the Vim and SQLite data; the Linux data was better fit by a power law (code+data):
I suspect that most of the deeply nested levels in Vim and SQLite are the results of long else if chains, which, while technically highly nested, could all have been written having the same nesting level, such as the following:
if (strcmp(x, "abc")) ; // code else if (strcmp(x, "xyz")) ; // code else if (strcmp(x, "123")) ; // code |
This if else pattern does not appear to be common in Linux. Perhaps ‘regularizing’ the if else sequences in Vim and SQLite will move the distribution towards a power law (i.e., like Linux).
Average nesting depth will also be affected by the average number of lines per function, with functions containing more statements providing the opportunity for more deeply nested if-statements (rather than calling a function containing nested if-statements).
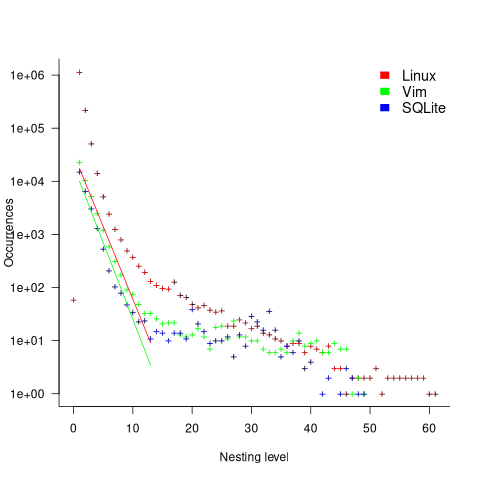
The plot below shows the number of occurrences of conditions containing a given number of clauses. Neither the exponential and power law are good fits, and log-log axis are used because it shows the points are closer to forming a straight line (code+data):
The plot below shows the nesting level and number of clauses in the condition for each of the 1,446,872 if-statements in the Linux kernel. Each value was ‘jittered’ to distribute points about their actual value, creating a more informative visualization (code+data):
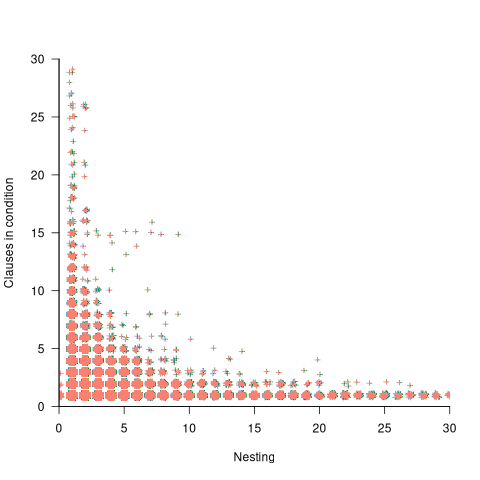
As expected, the likelihood of a condition containing multiple clauses does decrease with nesting level. However, with around 85% of conditions containing a single clause, the fitted regression models essential predict one clause for all nesting levels.
Motzkin paths and source code silhouettes
Consider a language that just contains assignments and if-statements (no else arm). Nesting level could be used to visualize programs written in such a language; an if represented by an Up step, an assignment by a Level step, and the if-terminator (e.g., the } token) by a Down step. Silhouettes for the nine possible four line programs are shown in the figure below (image courtesy of Wikipedia). I use the term silhouette because the obvious terms (e.g., path and trace) have other common usage meanings.

How many silhouettes are possible, for a function containing 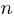 statements? Motzkin numbers provide the answer; the number of silhouettes for functions containing from zero to 20 statements is: 1, 1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019. The recurrence relation for Motzkin numbers is (where
statements? Motzkin numbers provide the answer; the number of silhouettes for functions containing from zero to 20 statements is: 1, 1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511, 41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019. The recurrence relation for Motzkin numbers is (where 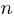 is the total number of steps, i.e., statements):
is the total number of steps, i.e., statements):
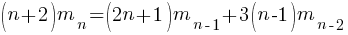
Human written code contains recurring patterns; the probability of encountering an if-statement, when reading code, is around 17% (at least for the C source of some desktop applications). What does an upward probability of 17% do to the Motzkin recurrence relation? For many years I have been keeping my eyes open for possible answers (solving the number theory involved is well above my mathematics pay grade). A few days ago I discovered weighted Motzkin paths.
A weighted Motzkin path is one where the Up, Level and Down steps each have distinct weights. The recurrence relationship for weighted Motzkin paths is expressed in terms of number of colored steps, where: 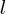 is the number of possible colors for the Level steps, and
is the number of possible colors for the Level steps, and 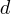 is the number of possible colors for Down steps; Up steps are assumed to have a single color:
is the number of possible colors for Down steps; Up steps are assumed to have a single color:
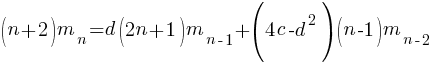
setting: 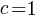 and
and 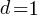 (i.e., all kinds of step have one color) recovers the original relation.
(i.e., all kinds of step have one color) recovers the original relation.
The different colored Level steps might be interpreted as different kinds of non-nesting statement sequences, and the different colored Down steps might be interpreted as different ways of decreasing nesting by one (e.g., a goto statement).
The connection between weighted Motzkin paths and probability is that the colors can be treated as weights that add up to 1. Searching on “weighted Motzkin” returns the kind of information I had been looking for; it seems that researchers in other fields had already discovered weighted Motzkin paths, and produced some interesting results.
If an automatic source code generator outputs the start of an if statement (i.e., an Up step) with probability 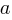 , an assignment (i.e., a Level step) with probability
, an assignment (i.e., a Level step) with probability 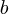 , and terminates the
, and terminates the if (i.e., a Down step) with probability 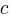 , what is the probability that the function will contain at least
, what is the probability that the function will contain at least 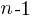 statements? The answer, courtesy of applying Motzkin paths in research into clone cell distributions, is:
statements? The answer, courtesy of applying Motzkin paths in research into clone cell distributions, is:
![P_n=sum{i=0}{delim{[}{(n-2)/2}{]}}(matrix{2}{1}{{n-2} {2i}})C_{2i}a^{i}b^{n-2-2i}c^{i+1} P_n=sum{i=0}{delim{[}{(n-2)/2}{]}}(matrix{2}{1}{{n-2} {2i}})C_{2i}a^{i}b^{n-2-2i}c^{i+1}](https://shape-of-code.com/wp-content/plugins/wpmathpub/phpmathpublisher/img/math_951_57086dac25a2ff31c2230f0791800e35.png)
where: 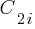 is the
is the 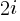 ‘th Catalan number, and that
‘th Catalan number, and that [...] is a truncation; code for an implementation in R.
In human written code we know that 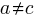 , because the number of statements in a compound-statement roughly has an exponential distribution (at least in C).
, because the number of statements in a compound-statement roughly has an exponential distribution (at least in C).
There has been some work looking at the number of peaks in a Motzkin path, with one formula for the total number of peaks in all Motzkin paths of length n. A formula for the number of paths of length 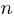 , having
, having 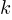 peaks, would be interesting.
peaks, would be interesting.
Motzkin numbers have been extended to what is called higher-rank, where Up steps and Level steps can be greater than one. There are statements that can reduce nesting level by more than one, e.g., breaking out of loops, but no constructs increase nesting by more than one (that I can think of). Perhaps the rather complicated relationship can be adapted to greater Down steps.
Other kinds of statements can increase nesting level, e.g., for-statements and while-statements. I have not yet spotted any papers dealing with the case where an Up step eventually has a corresponding Down step at the appropriate nesting level (needed to handle different kinds of nest-creating constructs). Pointers welcome. A related problem is handling if-statements containing else arms, here there is an associated increase in nesting.
What characteristics does human written code have that results in it having particular kinds of silhouettes? I have been thinking about this for a while, but have no good answers.
If you spot any Motzkin related papers that you think could be applied to source code analysis, please let me know.
Update
A solution to the Number of statement sequences possible using N if-statements problem.
for-loop usage at different nesting levels
When reading code, starting at the first line of a function/method, the probability of the next statement read being a for-loop is around 1.5% (at least in C, I don’t have decent data on other languages). Let’s say you have been reading the code a line at a time, and you are now reading lines nested within various if/while/for statements, you are at nesting depth 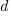 . What is the probability of the statement on the next line being a
. What is the probability of the statement on the next line being a for-loop?
Does the probability of encountering a for-loop remain unchanged with nesting depth (i.e., developer habits are not affected by nesting depth), or does it decrease (aren’t developers supposed to using functions/methods rather than nesting; I have never heard anybody suggest that it increases)?
If you think the for-loop use probability is not affected by nesting depth, you are going to argue for the plot on the left (below, showing number of loops whose compound-statement contains appearing in C source at various nesting depths), with the regression model fitting really well after 3-levels of nesting. If you think the probability decreases with nesting depth, you are likely to argue for the plot on the right, with the model fitting really well down to around 10-levels of nesting (code+data).
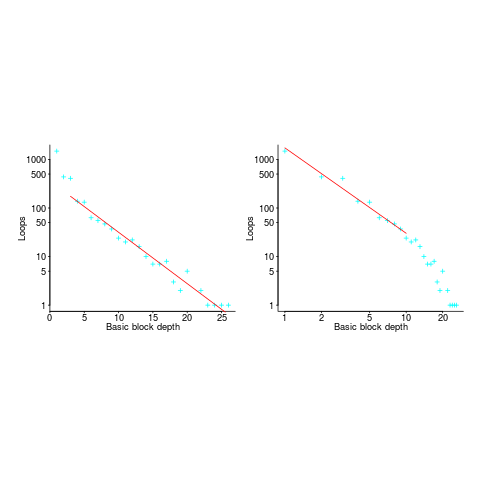
Both plots use the same data, but different scales are used for the x-axis.
If probability of use is independent of nesting depth, an exponential equation should fit the data (i.e., the left plot), decreasing probability is supported by a power-law (i.e, the right plot; plus other forms of equation, but let’s keep things simple).
The two cases are very wrong over different ranges of the data. What is your explanation for reality failing to follow your beliefs in for-loop occurrence probability?
Is the mismatch between belief and reality caused by the small size of the data set (a few million lines were measured, which was once considered to be a lot), or perhaps your beliefs are based on other languages which will behave as claimed (appropriate measurements on other languages most welcome).
The nesting depth dependent use probability plot shows a sudden change in the rate of decrease in for-loop probability; perhaps this is caused by the maximum number of characters that can appear on a typical editor line (within a window). The left plot (below) shows the number of lines (of C source) containing a given number of characters; the right plot counts tokens per line and the length effect is much less pronounced (perhaps developers use shorter identifiers in nested code). Note: different scales used for the x-axis (code+data).
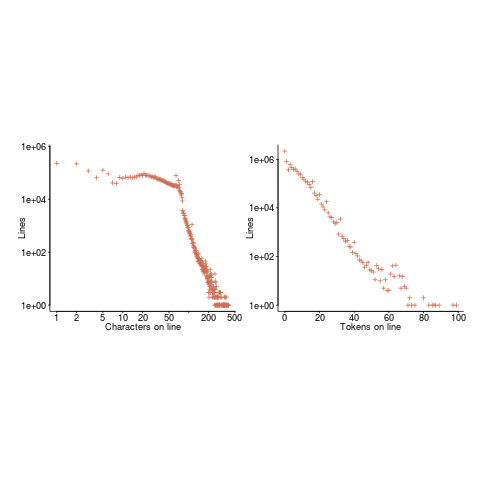
I don’t have any believable ideas for why the exponential fit only works if the first few nesting depths are ignored. What could be so special about early nesting depths?
What about fitting the data with other equations?
A bi-exponential springs to mind, with one exponential driven by application requirements and the other by algorithm selection; but reality is not on-board with this idea.
Ideas, suggestions, and data for other languages, most welcome.
Recent Comments