Archive
Halstead/McCabe: a complicated formula for LOC
My experience is that people prefer to ignore the implications of Halstead’s metric and McCabe’s complexity metric being strongly correlated (non-linearly) with lines of code (LOC). The implications being that they have been deluding themselves and perhaps wasting time/money using Halstead/McCabe when they could just as well have used LOC.
If the purpose of collecting metrics is a requirement to tick a box, then it does not really matter which metrics are collected. The Halstead/McCabe metrics have a strong brand, so why not collect them.
Don’t make the mistake of thinking that Halstead/McCabe is more than a complicated way of calculating LOC. This can be shown by replacing Halstead/McCabe by the corresponding LOC value to find that it makes little difference to the value calculated.
Some metrics include the Halstead metrics and/or the McCabe metric as part of their calculation. The Maintainability Index is a metric calculated using Halstead’s volume, McCabe’s complexity and lines of code. Its equation is (see below for details):
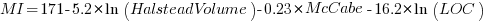
Replacing the Halstead/McCabe terms by one involving just LOC requires an appropriate mapping. Nearly all researchers assume a linear mapping, despite the overwhelming evidence that the mapping is non-linear.
Fitting regression models for HalsteadVolume vs LOC and McCabe vs LOC, using measurements of 730K methods from 47 Java projects (see below for data details), produces the coefficients for the equation needed to map each metric to LOC (previous analysis has found that a power law provides the best mapping; code+data). Substituting these equations in the Maintainability Index equation above, we get:
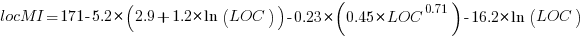
which simplifies to:
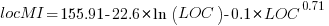
How does the value calculated using 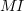 compare with the corresponding
compare with the corresponding 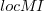 value?
value?
For 99.7% of methods, the relative error, 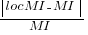 , for the 730K Java methods is less than 10%, and for 98.6% of methods the relative error is less than 5% (code+data).
, for the 730K Java methods is less than 10%, and for 98.6% of methods the relative error is less than 5% (code+data).
Given the fuzzy nature of these metrics, 10% is essentially noise.
Looking at the relative contributions made by Halstead/McCabe/LOC to the value of the Maintainability Index, second equation above, the Halstead contribution is around a third the size of the LOC contribution and the McCabe contribution is at least an order of magnitude smaller.
Background on the Maintainability Index and the measured Java projects.
The Maintainability Index was introduced in the 1994 paper “Construction and Testing of Polynomials Predicting Software Maintainability” by Oman, and Hagemeister (270 citations; no online pdf), a 1992 paper by the same authors is often incorrectly cited (426 citations). The earlier 1992 paper identified 92 known maintainability attributes, along with 60 metrics for “… gauging software maintainability …” (extracted from 35 published papers).
This Maintainability Index equation was chosen from “Approximately 50 regression models were constructed and tested in our attempts to identify simple models that could be calculated from existing tools and still be generic enough to be applied to a wide range of software.” The data fitted came from eight suites of programs (average LOC 3,568 per suite), along “… with subjective engineering assessments of the quality and maintainability of each set of code.”
Yes, choosing from 50 regression models looks like overfitting, and by today’s standards 28.5K LOC is a tiny amount of source.
The data used is distributed with the paper Revisiting the Debate: Are Code Metrics Useful for Measuring Maintenance Effort? by Chowdhury, Holmes, Zaidman, and Kazman, which does a good job of outlining the many different definitions of maintenance and the inconsistent results from prediction models. However, the authors remain under the street light of project source code, i.e., they ignore the fact that many maintenance requests are driven by demand for new features.
The authors investigate the impact of normalizing Halstead/McCabe by LOC, but make the common mistake of assuming a linear relationship. They are surprised by the high correlation between post-‘normalised’ Halstead/McCabe and LOC. The correlation disappears when the appropriate non-linear normalization is used; see code+data.
A 2014 paper by Najm also maps the components of the Maintainability Index to LOC, but uses a linear mapping from the Halstead/McCabe terms to LOC, creating a 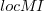 equation whose behavior is noticeably different.
equation whose behavior is noticeably different.
Halstead & McCabe metrics: The wisdom of the ancients
Study after study finds that the predictive power of both the Halstead metric and the McCabe cyclomatic complexity metric is no better than counting lines of code, for the characteristics of interest. Why do people continue to use and cite the Halstead and McCabe metrics?
My experience, talking to people, is that many believe these metrics have greater predictive power than lines of code. Sometimes I explain the situation, other times I move on.
Those who are aware of the facts often continue to use these metrics. Why do they do this?
Given the lack of alternative metrics that are more effective than lines of code, for the claimed uses of Halstead/McCabe, following the herd is the easy option (I regularly point this out to people, after explaining that Halstead/McCabe don’t do what is claimed on the tin). Tools are available to calculate the metrics; the manual effort is clicking buttons or running a command.
Why were the Halstead/McCabe metrics ‘successful’, in that they are the ones people cite/use today?
Both were formulated in the mid-1970s, when the discussion around measuring software started in earnest, so they had some first-mover advantage (within a few years they were both being suggested for use by US Military). Individuals promoted their ideas: Maurice Halstead was a senior professor, with colleagues and lots of graduate students, who advertised the metric via their publications; Thomas McCabe was working for the NSA when his famous paper was published, and went on to form a company working in the area of source code analysis.
The Halstead/McCabe metrics can both be calculated by processing the source one line at a time (just count decision points for McCabe, no need for the pretentious graph theory stuff). In the 1970s, computer memory was often measured in kilobytes, which made it difficult to implement complicated metrics that required keeping dependency information in memory.
Metrics based on the subroutine/function/procedure/method as the measured unit of source code had an implementation and usage advantage over metrics based on larger units of code.
In the 1990s, object-oriented programming, in the form of C++ and then Java, took off. The common view, by those caught up in the times, was that object-oriented software was so different from what went before that it needed its own metrics.
The 1991 paper: Towards a Metrics Suite for Object Oriented Design, by Chidamber and Kemerer, introduced the six CK metrics (as they become known; 1992 update). The nearest this paper comes to citing the Halstead/McCabe work is to say: “Some early work has recognized the shortcomings of existing metrics and the need for new metrics especially designed for OO.” The paper followed in the footsteps of the earlier work in not providing any evidence for the claims made (the update contains histograms of metric values from a C++ project and a Smalltalk project).
The 1996 paper: Evaluating the Impact of Object-Oriented Design on Software Quality, by Abreu and Melo, introduced the MOOD metrics (Metrics for Object-Oriented Design).
At the end of 2022 the total citation counts returned by Google Scholar were: McCabe 8,670, Halstead 4,900, CK 8,160, and MOOD 354.
The plot below shows the number of new citations returned by Google Scholar, each year, for the respective metrics papers (or book for Halstead; code+data):
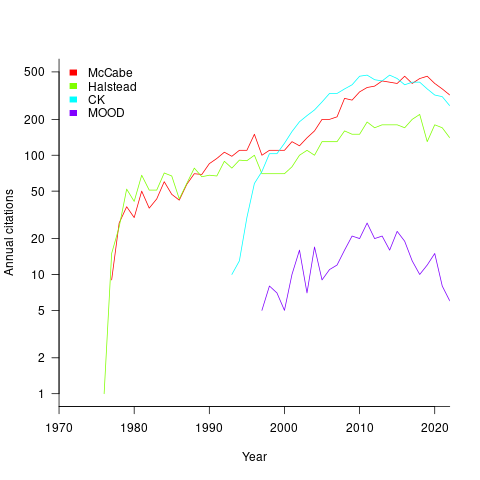
The ongoing growth in annual rate of citation probably has more to do with the growth in the number of software papers published each year, rather than these metric papers being cited by an expanding number of research fields.
Do authors tend to cite one or the other of Halstead/McCabe, or both?
Using Google Scholar’s ‘search within’ option to find the subset of papers that included a string matching the title of a paper: 46% of the Halstead citations include a citation of the McCabe paper, and 25% of the McCabe citations include a citation of the Halstead paper.
The Inciteful’s paper network (with citation counts: Halstead 1,052 and McCabe 4,970) found 657 papers citing both (62% of the Halstead total, 12% of the McCabe).
It’s not possible to make use of the OpenCitations API because it is DOI based, and the Halstead citation is a book.
The wisdom of the ancients
The software engineering ancients are people like Halstead and McCabe, along with less well known ancients (because they don’t name anything after them) such as Boehm for cost estimation, Lehman for software evolution, and Brooks because of a book; these ancients date from before 1980.
Why is the wisdom of these ancients still venerated (i.e., people treat them as being true), despite the evidence that they are very inaccurate (apart from Brooks)?
People hate a belief vacuum, they want to believe things.
The correlation between Halstead’s and McCabe’s metrics, and various software characteristics is no better than counting lines of code, but using a fancy formula feels more sophisticated and everybody else uses them, and we don’t have anything more accurate.
That last point is the killer, in many (most?) cases we don’t have any metrics that perform better than counting lines of code (other than taking the log of the number of lines of code).
Something similar happened in astronomy. Placing the Earth at the center of the solar system results in inaccurate predictions of where the planets are going to be in the sky; adding epicycles to the model helps to reduce the error. Until Newton came along with a model that produced very accurate results, people stuck with what they knew.
The continued visibility of COCOMO is a good example of how academic advertising (i.e., publishing papers) can keep an idea alive. Despite being more sophisticated, the Putnam model is not nearly as well known; Putnam formed a consulting company to promote this model, and so advertised to a different market.
Both COCOMO and Putnam have lines of code as an integral component of their models, and there is huge variability in the number of lines written by different people to implement the same functionality.
People tend not to talk about Lehman’s quantitative work on software evolution (tiny data set, and the fitted equation is very different from what is seen today). However, Lehman stated enough laws, and changed them often enough, that it’s possible to find something in there that relates to today’s view of software evolution.
Brooks’ book “The Mythical Man-Month” deals with project progress and manpower; what he says is timeless. The problem is that while lots of people seem happy to cite him, very few people seem to have read the book (which is a shame).
There is a book coming out this year that provides lots of evidence that the ancient wisdom is wrong or at best harmless, but it does not contain more accurate models to replace what currently exists 🙁
McCabe’s cyclomatic complexity and accounting fraud
The paper in which McCabe proposed what has become known as McCabe’s cyclomatic complexity did not contain any references to source code measurements, it was a pure ego and bluster paper.
Fast forward 10 years and cyclomatic complexity, complexity metric, McCabe’s complexity…permutations of the three words+metrics… has become one of the two major magical omens of code quality/safety/reliability (Halstead’s is the other).
It’s not hard to show that McCabe’s complexity is a rather weak measure of program complexity (it’s about as useful as counting lines of code).
Just as it is possible to reduce the number of lines of code in a function (by putting all the code on one line), it’s possible to restructure existing code to reduce the value of McCabe’s complexity (which is measured for individual functions).
The value of McCabe’s complexity for the following function is 5 16, i.e., and there are 16 possible paths through the function:
int main(void) { if (W) a(); else b(); if (X) c(); else d(); if (Y) e(); else f(); if (Z) g(); else h(); } |
each if…else contains two paths and there are four in series, giving 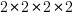 paths.
paths.
Restructuring the code, as below, removes the multiplication of paths caused by the sequence of if…else:
void a_b(void) {if (W) a(); else b();} void c_d(void) {if (X) c(); else d();} void e_f(void) {if (Y) e(); else f();} void g_h(void) {if (Z) g(); else h();} int main(void) { a_b(); c_d(); e_f(); g_h(); } |
reducing main‘s McCabe complexity to 1 and the four new functions each have a McCabe complexity of two.
Where has the ‘missing’ complexity gone? It now ‘exists’ in the relationship between the functions, a relationship that is not included in the McCabe complexity calculation.
The number of paths that can be traversed, by a call to main, has not changed (but the McCabe method for counting them now produces a different answer)
Various recommended practice documents suggest McCabe’s complexity as one of the metrics to consider (but don’t suggest any upper limit), while others go as far as to claim that it’s bad practice for functions to have a McCabe’s complexity above some value (e.g., 10) or that “Cyclomatic complexity may be considered a broad measure of soundness and confidence for a program“.
Consultants in the code quality/safety/security business need something to complain about, that is not too hard or expensive for the client to fix.
If a consultant suggested that you reduced the number of lines in a function by joining existing lines, to bring the count under some recommended limit, would you take them seriously?
What about, if a consultant highlighted a function that had an allegedly high McCabe’s complexity? Should what they say be taken seriously, or are they essentially encouraging developers to commit the software equivalent of accounting fraud?
Recent Comments