Archive
Employment in the software business: we know nothing
Tens of millions of people get paid to work on the creation and maintenance of software systems, by companies employing thousands of developers to those employing a single developer (in the UK there are almost 300K registered software companies; 5% of registered companies).
This huge ecosystem is almost completely ignored by the software engineering research community. Academics in computing/software are more interested in technical issue, and industry is an ecosystem they rarely interact with (some claim that student employment keeps them in contact with industry).
There are researchers in business and economics departments who study employment, e.g., careers, organization of workers and companies. The scientific study of work started at the beginning of the 1900s, originally focused on the manufacturing and included office work as that grew to employ a significant percentage of the workforce. Until recently, the percentage of the workforce employed to create/maintain software was not large enough to attract the attention of these researchers, and even now it’s often lumped together with other jobs that mostly involve some form of intellectual activity.
Employee related issues of interest to those involved in managing work on software systems are heavily influenced by the characteristics of the business ecosystem in which they work. The software driven business ecosystems are continually changing, with companies growing, merging and going bust as new markets emerge, grow, saturate, and sometime disappear. This constant change creates employment uncertainty, and lots of opportunities for competent people (creating a staff retention problem). For more stable industries, it’s possible for researchers to model employee start/promotion/leaving transitions using Markov models (example of ChatGPT 1o-preview solving a recurrence model of the staffing relationships in a 3-level employment hierarchy). The book “Stochastic Models for Social Processes” by D. J. Bartholomew gives a practical introduction to the use of Markov models for this kind of analysis.
The evolution and constant introduction of new technologies can make it difficult to find people with the appropriate skills. Companies may tune the wording of job adverts to give the impress of using ‘modern’ technologies, or post fake job adverts (to increase their attractiveness and suggest a feeling of growth), and people tune their CV to appeal to employers (some out right lie about their skills; many managers have told me that around 90% of applicants don’t have the primary skill sought by the employer). Well paid jobs can attract lots of applicants, filtering/interviewing can be an expensive process (not least because the same job title can denote different seniority in different companies). Matching CVs to job requirements sounds like the perfect use case for LLMs. I suspect that LLM tuning of CVs/adverts will just increase costs/uncertainty.
The constant churn of technologies forces employees to make decisions about whether to happily spend many years being well paid to become an expert in a niche with decreasing industry demand, or to invest in starting again as a non-expert doing something new (and initially less well paid).
What is the best to organize engineering employees at a company-wide scale? Matrix management was once the standard answer, but these days, scaled agile is a fashionable answer. An evidence-based answer will have to wait until the lawyers in a large organization allow somebody with the necessary skills access to the appropriate data.
With the contents of job sites being scraped, along with LinkedIn, I’m optimistic that some meaningful employment data will slowly become available. Will the analysis of this data uncover patterns of practical use (other than interesting blog posts) to employers/employees? We will have to wait and see.
Multi-state survival modeling of a Jira issues snapshot
Work items in a formal development process progress through a series of stages, e.g., starting at Open, perhaps moving to Withdrawn or Merged with another item, eventually reaching Development, and finishing at Done (with a few being Reopened, i.e., moving back to the start of the process).
This process can be modelled as a Markov chain, provided data on each stage of the process is available, for each work item; allowing values such as average time spent in each state and transition probabilities to be calculated.
The Jira issue/task/bug/etc tracking system has an option to generate a snapshot of the current status of work items in the system. The snapshot information on each item includes: start-date, current-state, time-in-state, date-of-snapshot.
If we assume that all work items pass through the same sequence of states, from Open to Done, then the snapshot contains enough information to build a multi-state survival model.
The key information is time-in-state, which can be used to calculate the date/time when an item transitioned from its previous state to its current state, providing a required link between all states.
How is a multi-state survival model better than creating a distinct survival model for each state?
The calculation of each state in a multi-state model takes into account information from the succeeding state, i.e., the time-in-state value in the succeeding state provides timing (from the Start state) on when a work item transitioned from its previous state. While this information could be added to each of the distinct models, it’s simpler to bundle everything together in one model.
A data analysis article by Robert Krasinski linked to the data used 🙂 The data does not include a description of the columns, but most of the names appear self-explanatory (I have no idea what key might be). Each of the 3,761 rows includes a story-point estimate, team-id, and a tag name for the work item.
Building a multi-state model provides a means for estimating the impact of team-id and story-points on time-in-state. I would expect items with higher story-point estimates to spend longer in Development, but I’m not sure how much difference there will be on other states.
I pruned the 22 states present in the data down to the following sequence of 13. Items might be Withdrawn or Merged with others items at any time, but I’m keeping things simple. These two states should also be absorbing in that there is no exit from them, I faked this by adding a transition to Done.
Open
Withdrawn
Merged
Backlog
In Analysis
In Refinement
Ready for Development
In Development
Code Review
Ready for Test
In Testing
Ready for Signoff
Done |
I’m familiar with building survival models, but have only ever built a couple of multi-state survival models. R supports several packages, which is the best one to use for this minimalist multi-state dataset?
The msm package is very much into state transition probabilities, or at least that is the impression I got from reading its manual. flexsurv and mstate are other packages I looked at. I decided to stay with the survival package, the default for simpler problems; the manuals contained lots of examples and some of them appeared similar to my problem.
Each row of work item information in the Jira snapshot looks something like the following:
X daysInStatus start status obsdate 1 0.53 2020-05-12 In Development 2020-05-18 |
This work item transitioned from state Ready for Development at time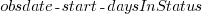 
to state In Development at time 
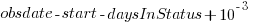, and was still in state In Development at time 
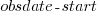(when the snapshot was taken); the 
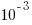is a small interval used to separate the states.
As is often the case with R packages, most of the work went into figuring out how to call the library functions with the data formatted just so, plus of course my own misunderstandings. Once the data was cleaned and process, the analysis was one line of code plus one to print the results; for instance, to estimate the mean time in each state by story-point value (code+data):
sp_fit=survfit(Surv(tstop-tstart, state) ~ sp, data=merged_status) print(sp_fit) |
Given the uncertainties in this model building process, I’m not going to discuss the results. This post is a proof of concept, which others can apply when the sequence of states is known with some degree of confidence, and good reasons for noise in the data are available.
Superoptimizers are back in vogue
There has always been the need for a few developers with in-depth knowledge of a particular cpu architecture to sit down and think very hard about how best to implement a snippet of code performing some operation in assembly language, e.g., library implementors wanting the tightest code for a critical inner loop or compiler writers who need to map from intermediate code to machine code.
In 1987 Massalin published his now famous paper that introduced the term Superoptimizer; a program that enumerates all possible combinations of instruction sequences until the shortest/fastest one producing the desired output from the given input is found (various heuristics were used to prune the search space e.g., only considering 15 or so opcodes, and the longest sequence it ever generated contained 12 instructions).
While the idea was widely talked about, it never caught on in practice (a special purpose branch eliminator was produced for GCC; Hacker’s Delight also includes a stand-alone system). Perhaps the guild of mindbogglingly-obtuse-but-fast-instruction-sequences black-balled it (apprentices have to spend several years doing nothing but writing assembly code for their chosen architecture, thinking about how to make it go faster and/or be shorter and only talk to other apprentices/members and communicate with non-converts exclusively about their latest neat sequence), or perhaps it was just a case of not invented here (writing machine code used to be something that even run-of-the-mill developers got to do every now and again), or perhaps it was not considered cost-effective to build a superoptimizer for a given project (I don’t know of anyone offering a generic tool that could be tailored for specific cases) or perhaps developers were happy to just ride the wave of continually faster processors.
It was not until 2008 with Bansal’s thesis that superoptimizer research started to take off (as in paper publication rate increased from once every five years to more than one a year). Bansal found a new market, binary translation i.e., translating the binary of a program built to run on one kind of cpu to run on a different kind of cpu, for instance the Mac 68K emulator.
Bansal and other researchers’ work was oriented towards relatively short instruction sequences. To be really useful, some way of handling longer sequences was needed.
A few days ago Stochastic Superoptimization arrived on the scene (or rather a paper describing it became available for download). Schkufza, Sharma and Aiken use Markov chain Monte Carlo methods to sample the possible instruction sequences rather than generating all of them. The paper gives a 116 instruction example from which the author’s tool removed 16 lines to produce code that went 1.6 times faster (only 30 ‘core’ instructions were given in paper); what is also very interesting is that the tool operates on compiler generated output (gcc/llvm), suggesting the usage build program, profile it and then stochastic superoptimize the hot spots.
Markov chains and Monte Carlo methods are trendy topics that researchers like to write about, so we will certainly see more papers in this area.
These days few developers have had hands-on experience with machine code, so the depth of expertise that was once easy to find is now rare, processors have many more weird and wonderful instructions often interacting with older instructions in obscure ways, and the cpu architecture landscape continues to change regularly. The time may have arrived for superoptimizers to be widely used by industry.
Of course, superoptimizers can work at any level of abstraction, including expression trees built directly from some complicated floating-point calculation that needs to be optimized for accuracy or speed.
Estimating the reliability of compiler subcomponent
Compiler stress testing can be used for more than finding bugs in compilers, it can also be used to obtain information about the reliability of individual components of a compiler. A recent blog post by John Regehr, lead investigator for the Csmith project, covered a proposal to improve an often overlooked aspect of automated compiler stress testing (removing non-essential code from a failing test case so it is small enough to be acceptable in a bug report; attaching 500 lines of source to a report in a sure fire way for it to be ignored) triggered this post. I hope that John’s proposal is funded and it would be great if the researchers involved also received funding to investigate component reliability using the data they obtain.
One process for estimating the reliability of the components of a compiler, or any other program, is:
- divide the compiler into a set of subcomponents. These components might be a collection of source files obtained through cluster analysis of the source, obtained from a functional analysis of the implementation documents or some other means,
- count the number of times each component executes correctly and incorrectly (this requires associating bugs with components by tracing bug fixes to the changes they induce in source files; obtaining this information will consume the largest amount of the human powered work) while processing lots of source. The ratio of these two numbers, for a given component, is an estimate of the reliability of that component.
How important is one component to the overall reliability of the whole compiler? This question can be answered if the set of components is treated as a Markov chain and the component transition probabilities are obtained using runtime profiling (see Large Empirical Case Study of Architecture–based Software Reliability by Goševa-Popstojanova, Hamill and Perugupalli for a detailed discussion).
Reliability is a important factor in developers’ willingness to enable some optimizations. Information from a component reliability analysis could be used to support an option that only enabled optimization components having a reliability greater than a developer supplied value.
The one big threat to validity of this approach is that stress tests are not representative of typical code. One possibility is to profile the compiler processing lots of source (say of the order of a common Linux distribution) and merge the transition probabilities, probably weighted, to those obtained from stress tests.
Recent Comments