Archive
Readability of anonymous inner classes and lambda expressions
The available evidence on readability is virtually non-existent, mostly consisting of a handful of meaningless experiments.
Every now and again somebody runs an experiment comparing the readability of X and Y. All being well, this produces a concrete result that can be published. I think that it would be a much more effective use of resources to run eye tracking experiments to build models of how people read code, but then I’m not on the publish or perish treadmill.
One such experimental comparison of X and Y is the paper Two N-of-1 self-trials on readability differences between anonymous inner classes (AICs) and lambda expressions (LEs) on Java code snippets by Stefan Hanenberg (who ran some experiments on the benefits of strong typing) and Nils Mehlhorn.
How might the readability of X and Y be compared (e.g., Java anonymous inner classes and lambda expressions)?
If the experimenter has the luxury of lots of subjects, then half of the subjects can be assigned to use X and half to use Y. When only a few subjects are available, perhaps as few as one, an N-of-1 experimental design can be used.
This particular study is worth discussing because it appears to be thought out and well run, as well as illustrating the issues involved in running such experiments, not because the readability of the two constructs is of particular interest. I think that developer choice of anonymous inner classes or lambda expressions is based on fashion and/or habit, and developers will claim the construct they use is the most readable one for them.
The Hanenberg and Mehlhorn study involved two experiments, using a N-of-1 design. In the first experiment task, subjects saw a snippet of code and had to count the number of parameters in either the anonymous inner class or the lambda expression (whose parameters were either untyped or typed); in the second experiment task subjects had to count the number of defined parameters that were used in the body of the anonymous inner class or lambda expression. English words were used for parameter names.
Each of the eight subjects saw the same set of randomly shuffled distinct 600 code snippets. The time taken to answer and correct/incorrect answer status were recorded. The snippets varied in the number of parameters and kind of construct; for task 1: 0-4 parameters, 3-kinds of construct, repeated 40 times, giving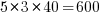 
distinct snippets; for task 2: 0-3 parameters used out of 3 parameters, 3-kinds of construct, repeated 50 times, giving 
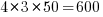distinct snippets.
The first task requires subjects to locate the definition of the construct, count the number of parameters, and report the count. The obvious model is different constructs require different amounts of time to locate, and that each parameter adds a fixed amount to the response time; there may be a small learning component.
Fitting a simple regression model shows (depending on choice of outlier bounds) that averaged over all subjects each parameter increased response time by around 80 msec, and that response was faster for lambda expressions (around 200 msec without parameter types, 90 msec if types are present); code+data. However, the variation across subjects had a standard deviation that was similar to these means.
The second task required subjects to read the body of the code, to find out which parameters were used. The mean response time increased from 1.5 to 3.7 seconds.
I was not sure whether to expect response time to increase or decrease as the number of parameters used in the body of the code increased (when the actual number of parameters is always three).
A simple fitted regression model finds that increase/decrease behavior varies between subjects (around 50 msec per parameter used); code+data. I am guessing that performance behavior depends on the mental model used to hold the used/not yet used information.
The magnitude of the performance differences found in this study mimics that seen in most human based software engineering experiments, that is, the impact of the studied construct is very small.
Some human biases in conditional reasoning
Tracking down coding mistakes is a common developer activity (for which training is rarely provided).
Debugging code involves reasoning about differences between the actual and expected output produced by particular program input. The goal is to figure out the coding mistake, or at least narrow down the portion of code likely to contain the mistake.
Interest in human reasoning dates back to at least ancient Greece, e.g., Aristotle and his syllogisms. The study of the psychology of reasoning is very recent; the field was essentially kick-started in 1966 by the surprising results of the Wason selection task.
Debugging involves a form of deductive reasoning known as conditional reasoning. The simplest form of conditional reasoning involves an input that can take one of two states, along with an output that can take one of two states. Using coding notation, this might be written as:
if (p) then q if (p) then !q if (!p) then q if (!p) then !q |
The notation used by the researchers who run these studies is a 2×2 contingency table (or conditional matrix):
OUTPUT
1 0
1 A B
INPUT
0 C D |
where: A, B, C, and D are the number of occurrences of each case; in code notation, p is the input and q the output.
The fertilizer-plant problem is an example of the kind of scenario subjects answer questions about in studies. Subjects are told that a horticultural laboratory is testing the effectiveness of 31 fertilizers on the flowering of plants; they are told the number of plants that flowered when given fertilizer (A), the number that did not flower when given fertilizer (B), the number that flowered when not given fertilizer (C), and the number that did not flower when not given any fertilizer (D). They are then asked to evaluate the effectiveness of the fertilizer on plant flowering. After the experiment, subjects are asked about any strategies they used to make judgments.
Needless to say, subjects do not make use of the available information in a way that researchers consider to be optimal, e.g., Allan’s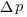 
index 
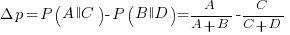(sorry about the double, 
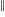, rather than single, vertical lines).
What do we know after 40+ years of active research into this basic form of conditional reasoning?
The results consistently find, for this and other problems, that the information A is given more weight than B, which is given by weight than C, which is given more weight than D.
That information provided by A and B is given more weight than C and D is an example of a positive test strategy, a well-known human characteristic.
Various models have been proposed to ‘explain’ the relative ordering of information weighting: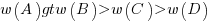 
, e.g., that subjects have a bias towards sufficiency information compared to necessary information.
Subjects do not always analyse separate contingency tables in isolation. The term blocking is given to the situation where the predictive strength of one input is influenced by the predictive strength of another input (this process is sometimes known as the cue competition effect). Debugging is an evolutionary process, often involving multiple test inputs. I’m sure readers will be familiar with the situation where the output behavior from one input motivates a misinterpretation of the behaviour produced by a different input.
The use of logical inference is a commonly used approach to the debugging process (my suggestions that a statistical approach may at times be more effective tend to attract odd looks). Early studies of contingency reasoning were dominated by statistical models, with inferential models appearing later.
Debugging also involves causal reasoning, i.e., searching for the coding mistake that is causing the current output to be different from that expected. False beliefs about causal relationships can be a huge waste of developer time, and research on the illusion of causality investigates, among other things, how human interpretation of the information contained in contingency tables can be ‘de-biased’.
The apparently simple problem of human conditional reasoning over two variables, each having two states, has proven to be a surprisingly difficult to model. It is tempting to think that the performance of professional software developers would be closer to the ideal, compared to the typical experimental subject (e.g., psychology undergraduates or Mturk workers), but I’m not sure whether I would put money on it.
A study of deceit when reporting information in a known context
A variety of conflicting factors intrude when attempting to form an impartial estimate of the resources needed to perform a task. The customer/manager, asking for the estimate, wants to hear a low value, creating business/social pressure to underestimate; overestimating increases the likelihood of completing the task within budget.
A study by Oey, Schachner and Vul investigated the strategic reasoning for deception/lying in a two-person game.
A game involved a Sender and Receiver, with the two players alternating between the roles. The game started with both subjects seeing a picture of a box containing red and blue marbles (the percentage of red marbles was either 20%, 50%, or 80%). Ten marbles were randomly selected from this ‘box’, and shown to the Sender. The Sender was asked to report to the Receiver the number of red marbles appearing in the random selection,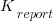 
(there was an incentive to report higher/lower, and punishment for being caught being inaccurate). The Receiver could accept or reject the number of red balls reported by the Sender. In the actual experiment, unknown to the human subjects, one of every game’s subject pair was always played by a computer. Every subject played 100 games.
In the inflate condition: If the Receiver accepted the report, the Sender gained points, and the Receiver gained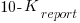 
points.
If the Receiver rejected the report, then:
- if the Sender’s report was accurate (i.e., ==
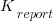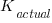), the Sender gained 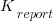points, and the Receiver gained 
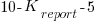points (i.e., a -5 point penalty), - if the Sender’s report was not accurate, the Receiver gained 5 points, and the Sender lost 5 points.
In the deflate condition: The points awarded to the Sender was based on the number of blue balls in the sample, and the points awarded to the Received was based on the number of red balls in the sample (i.e., the Sender had in incentive to report fewer red balls).
The plot below shows the mean rate of deceit (i.e., the fraction of a subject’s reports where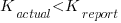 
, averaged over all 116 subject’s mean) for a given number of red marbles actually seen by the Sender; vertical lines show one standard deviation, calculated over the mean of all subjects (code+data):
Subjects have some idea of the percentage of red/blue balls, and are aware that their opponent has a similar idea.
The wide variation in the fraction of reports where a subject reported a value greater than the number of marbles seen, is likely caused by variation in subject level of risk aversion. Some subjects may have decided to reduce effort by always accurately reporting, while others may have tried to see how much they could get away with.
The wide variation is particularly noticeable in the case of a box containing 80% red. If a Sender’s random selection contains few reds, then the Sender can feel confident reporting to have seen more.
The general pattern shows subjects being more willing to increase the reported number when they are supplied with few.
There is a distinct change of behavior when half of the sample contains more than five red marbles. In this situation, subjects may be happy to have been dealt a good hand, and are less inclined to risk losing 5-points for less gain.
Estimating involves considering more factors than the actual resources likely to be needed to implement the task; the use of round numbers is one example. This study is one of few experimental investigations of numeric related deception. The use of students having unknown motivation is far from ideal, but they are better than nothing.
When estimating in a team context, there is an opportunity to learn about the expectations of others and the consequences of over/under estimating. An issue for another study 🙂
Estimating quantities from several hundred to several thousand
How much influence do anchoring and financial incentives have on estimation accuracy?
Anchoring is a cognitive bias which occurs when a decision is influenced by irrelevant information. For instance, a study by John Horton asked 196 subjects to estimate the number of dots in a displayed image, but before providing their estimate subjects had to specify whether they thought the number of dots was higher/lower than a number also displayed on-screen (this was randomly generated for each subject).
How many dots do you estimate appear in the plot below?
Estimates are often round numbers, and 46% of dot estimates had the form of a round number. The plot below shows the anchor value seen by each subject and their corresponding estimate of the number of dots (the image always contained five hundred dots, like the one above), with round number estimates in same color rows (e.g., 250, 300, 500, 600; code+data):
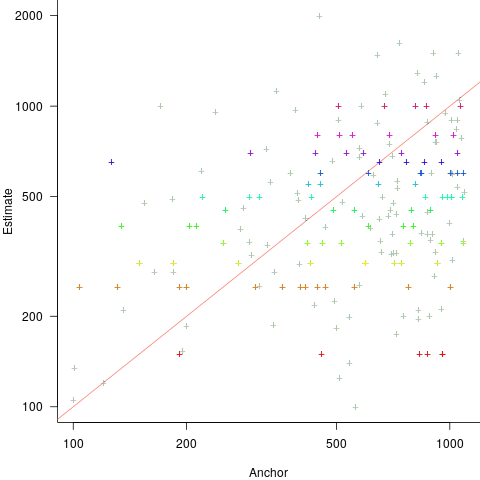
How much influence does the anchor value have on the estimated number of dots?
One way of measuring the anchor’s influence is to model the estimate based on the anchor value. The fitted regression equation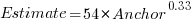 
explains 11% of the variance in the data. If the higher/lower choice is included the model, 44% of the variance is explained; higher equation is: 
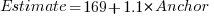and lower equation is: 
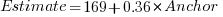(a multiplicative model has a similar goodness of fit), i.e., the anchor has three-times the impact when it is thought to be an underestimate.
How much would estimation accuracy improve if subjects’ were given the option of being rewarded for more accurate answers, and no anchor is present?
A second experiment offered subjects the choice of either an unconditional payment of $2.50 or a payment of $5.00 if their answer was in the top 50% of estimates made (labelled as the risk condition).
The 196 subjects saw up to seven images (65 only saw one), with the number of dots varying from 310 to 8,200. The plot below shows actual number of dots against estimated dots, for all subjects; blue/green line shows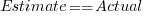 
, and red line shows the fitted regression model 
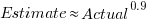(code+data):
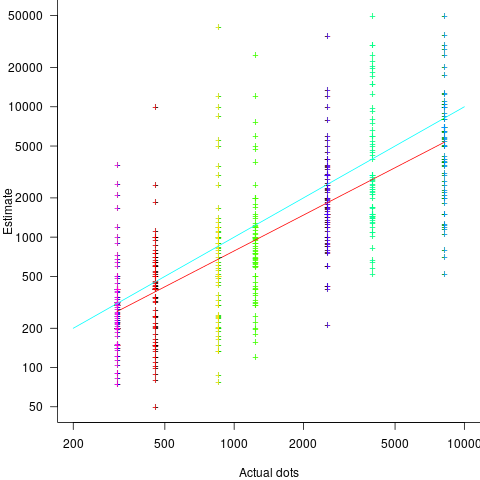
The variance in the estimated number of dots is very high and increases with increasing actual dot count, however, this behavior is consistent with the increasing variance seen for images containing under 100 dots.
Estimates were not more accurate in those cases where subjects chose the risk payment option. This is not surprising, performance improvements require feedback, and subjects were not given any feedback on the accuracy of their estimates.
Of the 86 subjects estimating dots in three or more images, 44% always estimated low and 16% always high. Subjects always estimating low/high also occurs in software task estimates.
Estimation patterns previously discussed on this blog have involved estimated values below 100. This post has investigated patterns in estimates ranging from several hundred to several thousand. Patterns seen include extensive use of round numbers and increasing estimate variance with increasing actual value; all seen in previous posts.
How useful are automatically generated compiler tests?
Over the last decade, testing compilers using automatically generated source code has been a popular research topic (for those working in the compiler field; Csmith kicked off this interest). Compilers are large complicated programs, and they will always contain mistakes that lead to faults being experienced. Previous posts of mine have raised two issues on the use of automatically generated tests: a financial issue (i.e., fixing reported faults costs money {most of the work on gcc and llvm is done by people working for large companies}, and is intended to benefit users not researchers seeking bragging rights for their latest paper), and applicability issue (i.e., human written code has particular characteristics and unless automatically generated code has very similar characteristics the mistakes it finds are unlikely to commonly occur in practice).
My claim that mistakes in compilers found by automatically generated code are unlikely to be the kind of mistakes that often lead to a fault in the compilation of human written code is based on the observations (I don’t have any experimental evidence): the characteristics of automatically generated source is very different from human written code (I know this from measurements of lots of code), and this difference results in parts of the compiler that are infrequently executed by human written code being more frequently executed (increasing the likelihood of a mistake being uncovered; an observation based on my years working on compilers).
An interesting new paper, Compiler Fuzzing: How Much Does It Matter?, investigated the extent to which fault experiences produced by automatically generated source are representative of fault experiences produced by human written code. The first author of the paper, Michaël Marcozzi, gave a talk about this work at the Papers We Love workshop last Sunday (videos available).
The question was attacked head on. The researchers instrumented the code in the LLVM compiler that was modified to fix 45 reported faults (27 from four fuzzing tools, 10 from human written code, and 8 from a formal verifier); the following is an example of instrumented code:
warn ("Fixing patch reached"); if (Not.isPowerOf2()) { if (!(C-> getValue().isPowerOf2() // Check needed to fix fault && Not != C->getValue())) { warn("Fault possibly triggered"); } else { /* CODE TRANSFORMATION */ } } // Original, unfixed code |
The instrumented compiler was used to build 309 Debian packages (around 10 million lines of C/C++). The output from the builds were (possibly miscompiled) built versions of the packages, and log files (from which information could be extracted on the number of times the fixing patches were reached, and the number of cases where the check needed to fix the fault was triggered).
Each built package was then checked using its respective test suite; a package built from miscompiled code may successfully pass its test suite.
A bitwise compare was run on the program executables generated by the unfixed and fixed compilers.
The following (taken from Marcozzi’s slides) shows the percentage of packages where the fixing patch was reached during the build, the percentages of packages where code added to fix a fault was triggered, the percentage where a different binary was generated, and the percentages of packages where a failure was detected when running each package’s tests (0.01% is one failure):
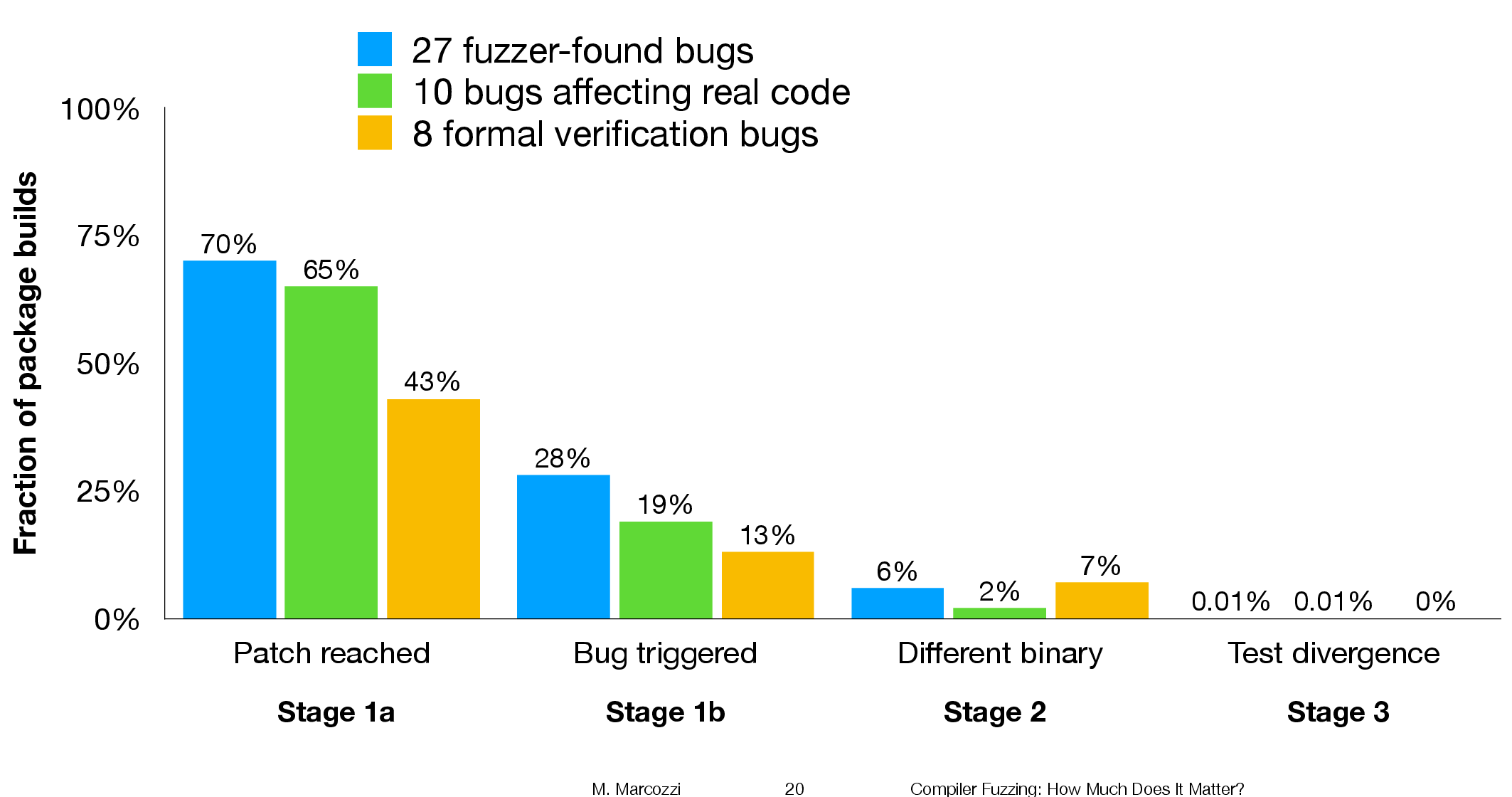
The takeaway from the above figure is that many packages are affected by the coding mistakes that have been fixed, but that most package test suites are not affected by the miscompilations.
To find out whether there is a difference, in terms of impact on Debian packages, between faults reported in human and automatically generated code, we need to compare the number of occurrences of “Fault possibly triggered”. The table below shows the break-down by the detector of the coding mistake (i.e., Human and each of the automated tools used), and the number of fixed faults they contributed to the analysis.
Human, Csmith and EMI each contributed 10-faults to the analysis. The fixes for the 10-fault reports in human generated code were triggered 593 times when building the 309 Debian packages, while each of the 10 Csmith and EMI fixes were triggered 1,043 and 948 times respectively; a lot more than the Human triggers :-O. There are also a lot more bitwise compare differences for the non-Human fault-fixes.
Detector Faults Reached Triggered Bitwise-diff Tests failed Human 10 1,990 593 56 1 Csmith 10 2,482 1,043 318 0 EMI 10 2,424 948 151 1 Orange 5 293 35 8 0 yarpgen 2 608 257 0 0 Alive 8 1,059 327 172 0 |
Is the difference due to a few packages being very different from the rest?
The table below breaks things down by each of the 10-reported faults from the three Detectors.
Ok, two Human fault-fix locations are never reached when compiling the Debian packages (which is a bit odd), but when the locations are reached they are just not triggering the fault conditions as often as the automatic cases.
Detector Reached Triggered
Human
300 278
301 0
305 0
0 0
0 0
133 44
286 231
229 0
259 40
77 0
Csmith
306 2
301 118
297 291
284 1
143 6
291 286
125 125
245 3
285 16
205 205
EMI
130 0
307 221
302 195
281 32
175 5
122 0
300 295
297 215
306 191
287 10 |
It looks like I am not only wrong, but that fault experiences from automatically generated source are more (not less) likely to occur in human written code (than fault experiences produced by human written code).
This is odd. At best, I would expect fault experiences from human and automatically generated code to have the same characteristics.
Ideas and suggestions welcome.
Update: the morning after
I have untangled my thoughts on how to statistically compare the three sets of data.
The bootstrap is based on the idea of exchangeability; which items being measured might we consider to be exchangeable, i.e., being able to treat the measurement of one as being the equivalent to measuring the other.
In this experiment, the coding mistakes are not exchangeable, i.e., different mistakes can have different outcomes.
But we might claim that the detection of mistakes is exchangeable; that is, a coding mistake is just as likely to be detected by source code produced by an automatic tool as source written by a Human.
The bootstrap needs to be applied without replacement, i.e., each coding mistake is treated as being unique. The results show that for the sum of the Triggered counts (code+data):
- treating Human and Csmith as being equally likely to detect the same coding mistake, there is a 18% change of the Human results being lower than 593.
- treating Human and EMI as being equally likely to detect the same coding mistake, there is a 12% change of the Human results being lower than 593.
So the likelihood of the lower value, 593, of Human Triggered events is expected to occur quite often (i.e., 12% and 18%). Automatically generated code is not more likely to detect coding mistakes than human written code (at least based on this small sample set).
Using identifier prefixes results in more developer errors
Human speech communication has to be processed in real time using a cpu with a very low clock rate (i.e., the human brain whose neurons fire at rates between 10-100 Hz). Biological evolution has mitigated the clock rate problem by producing a brain with parallel processing capabilities and cultural evolution has chipped in by organizing the information content of languages to take account of the brains strengths and weaknesses. Words provide a good example of the way information content can be structured to be handled by a very slow processor/memory system, e.g., 85% of English words start with a strong syllable (for more details search for initial in this detailed analysis of human word processing).
Given that the start of a word plays an important role as an information retrieval key we would expect the code reading performance of software developers to be affected by whether the identifiers they see all start with the same letter sequence or all started with different letter sequences. For instance, developers would be expected to make fewer errors or work quicker when reading the visually contiguous sequence consoleStr, startStr, memoryStr and lineStr, compared to say strConsole, strStart, strMemory and strLine.
An experiment I ran at the 2011 ACCU conference provided the first empirical evidence of the letter prefix effect that I am aware of. Subjects were asked to remember a list of four assignment statements, each having the form id=constant;, perform an unrelated task for a short period of time and then recall information about the previously seen constants (e.g., their value and which variable they were assigned to).
During recall subjects saw a list of five identifiers and one of the questions asked was which identifier was not in the previously seen list? When the list of identifiers started with different letters (e.g., cat, mat, hat, pat and bat) the error rate was 2.6% and when the identifiers all started with the same letter (e.g., pin, pat, pod, peg, and pen) the error rate was 5.9% (the standard deviation was 4.5% and 6.8% respectively, but ANOVA p-value was 0.038). Having identifiers share the same initial letter appears to double the error rate.
This looks like great news; empirical evidence of software developer behavior following the predictions of a model of human human speech/reading processing. A similar experiment was run in 2006, this asked subjects to remember a list of three assignment statements and they had to select the ‘not seen’ identifier from a list of four possibilities. An analysis of the results did not find any statistically significant difference in performance for the same/different first letter manipulation.
The 2011/2006 experiments throw up lots of questions, including: does the sharing a prefix only make a difference to performance when there are four or more identifiers, how does the error rate change as the number of identifiers increases, how does the error rate change as the number of letters in the identifier change, would the effect be seen for a list of three identifiers if there was a longer period between seeing the information and having to recall it, would the effect be greater if the shared prefix contained more than one letter?
Don’t expect answers to appear quickly. Experimenting using people as subjects is a slow, labour intensive process and software developers don’t always answer the question that you think they are answering. If anybody is interested in replicating the 2011 experiment the tools needed to generate the question sheets are available for download.
For many years I have strongly recommended that developers don’t prefix a set of identifiers sharing some attribute with a common letter sequence (its great to finally have some experimental backup, however small). If it is considered important that an attribute be visible in an identifiers spelling put it at the end of the identifier.
See you all at the ACCU conference tomorrow and don’t forget to bring a pen/pencil. I have only printed 40 experiment booklets, first come first served.
Generating code that looks like it is human written
I am very interested in understanding the patterns of developer behavior that lead to the human characteristics that can be found in code. To help me get some idea of how well I understand this behavior I have decided to build a tool that generates source code that appears to be written by human programmers. I hope to reach a point where I can offer a challenge to tell the difference between generated code and human written code.
The three main production techniques I plan to use are, in increasing order of relatedness to humans production techniques, are:
- Random generation based on percentage occurrence of language constructs obtained from measurements of existing source. This is the simplest approach and the one furthest away from common developer behavior; even so there are things that can be learned from this information. For instance, the theory that developers are more likely to create a function once code becomes heavily nested code implies that the probability of encountering an if-statement decreases as nesting depth increases; measurements show the probability of encountering an if-statement remaining approximately constant as depth of nesting increases.
- Behavior templates. People have habits in everyday life and also when writing software. While some habits are idiosyncratic and not encountered very often there are some that appear to be generally used. For instance, developers tend to assign a fixed role to every variable they define (e.g., stepper for stepping through a succession of values and most-recent holder holding the latest value encountered in going through a succession of values).
I am expecting/hoping that generation by behavioral templates will result in code having some of the probabilistic properties seen in human code, removing the need for purely random generation driven by low level language probability measurements. For instance, the probability of a local variable appearing in a function is proportional to the percentage of its previous occurrences up to that point in the source of the function (
percentage = occurrences_of_X / occurrences_of_all_local_variables) and I am hoping that this property appears as emergent behavior from generating using the role of variable template. - Story telling. A program is like the plot of a story, it has a cast of characters (e.g., classes, functions, libraries) that perform various actions and interact with each other in order to achieve various goals, there are subplots (intermediate results are calculated, devices are initialized, etc), there are resource limits, etc.
While a lot of stories are application domain specific there are subplots common to many stories; also how a story is told can be heavily influenced by the language used, for instance Prolog programs have a completely different structure than those written in procedural languages such as Java. I want to stay away from being application specific and I don’t plan to tackle languages too far outside the common-or-garden procedural variety.
Researchers have created automatic story generators; the early generators were template based while more recent systems have used an agent based approach. Story based generation of code is my ideal, but I am a long way away from having enough knowledge of developer behavior to be more than template based.
In a previous post I described a system for automatically generating very simply C programs. I plan to build on this system to incrementally improve the ‘humanness’ of the generated code. At some point, hopefully before the end of this year, I will challenge people to tell the difference between automatically generated and human written code.
The language I have studied the most is C and this will be the main target. I don’t want to be overly C specific and am trying to decide on a good second language (i.e., lots of source available for measurement, used by lots of developers and not too different from C). JavaScript is the current front runner, it is a class-less object oriented language which is not ‘wildly’ OO (the patterns of usage in human written OO code continue to evolve at a rapid rate which can make a lot of human C++/Java code look automatically generated).
As well as being a test bed for understanding of human generated code other uses for an automatic generator include compiler stress testing and providing code snippets to an automated fault fixing tool.
Recent Comments