The Shape of Code

Changing the state of a digital circuit (i.e., changing its value from zero to one, or from one to zero) requires more electrical power than leaving its state unchanged. During program execution, the power consumed by each instruction depends on the value of its operand(s). The plot below, from an earlier post, shows how the power consumed by an 8-bit multiply instruction varies with the values of its two operands:

An increase in cpu power consumption produces an increase in its temperature. If the temperature gets too high, the cpu’s DVFS (dynamic voltage and frequency scaling) will slow down the processor to prevent it overheating.

When a calculation involves a huge number of values (e.g., an LLM size matrix multiply), how large an impact is variability of input values likely to have on the power consumed?

The 2022 paper: Understanding the Impact of Input Entropy on FPU, CPU, and GPU Power by S. Bhalachandra, B. Austin, S. Williams, and N. J. Wright, compared matrix multiple power consumption when all elements of the matrices had the same values (i.e., minimum entropy) and when all elements had different random values (i.e., maximum entropy).

The plot below shows the power consumed by an NVIDIA A100 Ampere GPU while multiplying two 16,384 by 16,384 matrices (performed 100 times). The GPU was power limited to 400W, so the random value performance was lower at 18.6 TFLOP/s, against 19.4 TFLOP/s for same values; (I don’t know why the startup times differ; code+data):

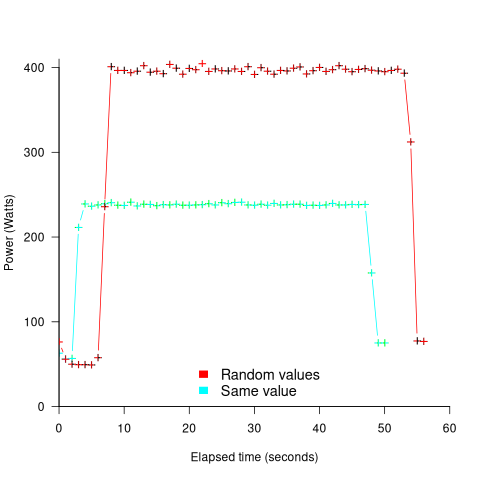
This 67% performance difference is more than an interesting factoid. Large computations are distributed over multiple GPUs, and the output from each GPU is sometimes feed as input to other GPUs. The flow of computations around a cluster of GPUs needs to be synchronised, and having compute time depend on the distribution of the input values makes life complicated.

Is it possible to organise a sequence of calculation to reduce the average power consumed?

The higher order bits of small integers are zero, but how many long calculations involve small integers? The bit pattern of floating-point values are more difficult to predict, but I’m sure there is a PhD thesis or two waiting to be written around this issue.