Archive
Variations in the literal representation of Pi
The numbers system I am developing attempts to match numeric literals contained in a file against a database of interesting numbers. One of the things I did to quickly build a reasonably sized database of reliable values was to extract numeric literals from a few well known programs that I thought I could trust.
R is a widely used statistical package, and Maxima is a computer algebra system with a long history. Both contain a great deal of functionality and are actively maintained.
To my surprise, the source code of both packages contain a large variety of different literal values for 
, or to be exact, the number of digits contained in the literals varied by more than I expected. In the following table, the value to the left of the representation is the number of occurrences; values listed in increasing literal order:
Maxima R
2 3.14159
14 3.141592
1 3.1415926
1 3.14159265 2 3.14159265
3 3.1415926535
4 3.14159265358979
14 3.141592653589793
3 3.1415926535897932385 3 3.1415926535897932385
9 3.14159265358979324
1 3.14159265359
1 3.1415927
1 3.141593
The comments in the Maxima source led me to believe that some thought had gone into ensuring that the numerical routines were robust. Over 3/4 of the literal representations of have a precision comparable to at least that of 64-bit floating-point (I’m assuming an IEEE 754 representation in this post).
In the R source, approximately 2/3 of the literal representations of have a precision comparable to that of 32-bit floating-point.
Closer examination of the source suggests one reason for this difference. Both packages make heavy use of existing code (translated from Fortran to Lisp for Maxima and from Fortran to C for R); using existing code makes good sense and because of its use in scientific and engineering applications many numerical libraries have been written in Fortran. Maxima has adapted the slatec library, whereas the R developers have used a variety of different libraries (e.g., specfun).
How important is variation in the representation of Pi?
- A calculation based on a literal that is only accurate to 32-bits is likely to be limited to that level of accuracy (unless errors cancel out somewhere).
- Inconsistencies in the value used to represent Pi are a source of error. These inconsistencies may be implicit, for instance literals used to denote a value derived from such as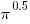
often seem to be based on more precise values of Pi than appear in the code.
The obvious solution to this representation issue of creating a file containing definitions of all the frequently used literal values has possible drawbacks. For instance, numerical accuracy is a strange beast, and increasing the precision of one literal without doing the same for other literals appearing in a calculation can sometimes reduce the accuracy of the final result.
Pulling together existing libraries to build a package is often very cost-effective, but numerical accuracy is a slippery beast, and this inconsistent usage of literals suggests that developers from these two communities have not addressed the system level consequences of software reuse.
Update 6 April: After further rummaging around in the R source distribution, I found that things are not as bad as they first appear. Only two of the single precision instances of listed above occur in the C or Fortran source code, the rest appear in support files (e.g., m4 scripts and R examples).
Using numeric literals to identify application domains
I regularly get to look at large quantities of source and need to quickly get some idea of the application domains used within the code; for instance, statistical calculations, atomic physics or astronomical calculations. What tool might I use to quickly provide a list of the application domains used within some large code base?
Within many domains some set of numbers are regularly encountered and for several years I have had the idea of extracting numeric literals from source and comparing them against a database of interesting numbers (broken down by application). I have finally gotten around to writing a program do this extraction and matching, its imaginatively called numbers. The hard part is creating an extensive database of interesting numbers and I’m hoping that that releasing everything under an open source license will encourage people to add their own lists of domain specific interesting numbers.
The initial release is limited to numeric literals containing a decimal point or exponent, i.e., floating-point literals. These tend to be much more domain specific than integer literals and should cut down on the noise, making it easier for me tune the matching algorithms without (currently numeric equality within some fuzz-factor and fuzzy-matching of digits in the mantissa).
Sometimes an algorithm uses a set of numbers (e.g., crc checking) and a match should only occur if all values from this set are encountered.
The larger the interesting number database the larger the probability of matching against a value from an unrelated domain. The list of atomic weights seem to be very susceptible to this problem. I am currently investigating whether the words that co-occur with an instance of a numeric literal can be used to reduce this problem, perhaps by requiring that at least one word from a provided list occur in the source before a match is flagged for some literal.
Some numbers frequently occur in several domains. I am hoping that the word analysis might also be used to help reduce the number of domains that need to be considered (ideally to one).
Another problem is how to handle conversion factors, that is the numeric constant used to convert one unit to another, e.g., meters to furlongs. What is needed is to calculate all unit conversion values from a small set of ‘basic’ units. It would probably be very interesting to find conversions between some rarely seen units occurring in source.
I have been a bit surprised by how many apparently non-interesting floating-point literals occur in source and am hoping that a larger database will turn them into interesting numbers (I suspect this will only occur for a small fraction of these literals).
Designing a processor for increased source portability costs
How might a vendor make it difficult for developers to port open source applications to their proprietary cpu? Keeping the instruction set secret is one technique, another is to design a cpu that breaks often relied upon assumptions that developers have about the characteristics of the architecture on which their code executes.
Of course breaking architectural assumptions does not prevent open source being ported to a platform, but could significantly slow down the migration; giving more time for customers to become locked into the software shipped with the product.
Which assumptions should be broken to have the maximum impact on porting open source? The major open source applications (e.g., Firefox, MySQL, etc) run on 32/64-bit architectures that have an unsigned address space, whose integer representation uses two’s complement arithmetic and arithmetic operations on these integer values wrap on over/underflow.
32/64-bit. There is plenty of experience showing that migrating code from 16-bit to 32-bit environments can involve a lot of effort (e.g., migrating Windows 286/386 code to the Intel 486) and plenty of companies are finding the migration from 32 to 64-bits costly.
Designing a 128-bit processor might not be cost effective, but what about a 40-bit processor, like a number of high end DSP chips? I suspect that there are many power-of-2 assumptions lurking in a lot of code. A 40-bit integer type could prove very expensive for ports of code written with a 32/64-bit mindset (dare I suggest a 20-bit short; DSP vendors have preferred 16-bits because it uses less storage?).
Unsigned address space (i.e., lowest address is zero). Some code assumes that addresses with the top bit set are at the top end of memory and not just below the middle (e.g., some garbage collectors). Processors having a signed address space (i.e., zero is in the middle of storage) are sufficiently rare (e.g., the Inmos Transputer) that source is unlikely to support a HAS_SIGNED_ADDRESS build option.
How much code might need to be rewritten? I have no idea. While the code is likely to be very important there might not be a lot of it.
Two’s complement. Developers are constantly told not to write code that relies on the internal representation of data types. However, they might be forgiven for thinking that nobody uses anything other than two’s complement to represent integer types these days (I suspect Univac does not have that much new code ported to it’s range of one’s complement machines).
How much code will break when ported to a one’s complement processor? The representation of negative numbers in one’s complement and two’s complement is different and the representation of positive numbers the same. In common usage positive values are significantly more common than negative values and many variables (having a signed type) never get to hold a negative value.
While I have no practical experience, or know of anybody who has, I suspect the use of one’s complement might not be that big a problem. If you have experience please comment.
Arithmetic that wraps (i.e., positive values overflow negative and negative values underflow positive). While expressions explicitly written to wrap might be rare, how many calculations contain intermediate values that have wrapped but deliver a correct final result because they are ‘unwrapped’ by a subsequent operation?
Arithmetic operation that saturate are needed in applications such as graphics where, for instance, increasing the brightness should not suddenly cause the darkest setting to occur. Some graphics processors include support for arithmetic operations that saturate.
The impact of saturation arithmetic on portability is difficult to judge. A lot of code contains variables having signed char and short types, but when they appear as the operand in a binary operation these are promoted to int in C/C++/etc which probably has sufficient range not to overflow (most values created during program execution are small). Again I am lacking in practical experience and comments are welcome.
Floating-point. Many programs do not make use of floating-point arithmetic and those that do rarely manipulate such values at the bit level. Using a non-IEEE 754 floating-point representation will probably have little impact on the portability of applications of interest to most users.
Update. Thanks to Cate for pointing out that I had forgotten to discuss why using non-8-bit chars does is not a worthwhile design decision.
Both POSIX and the C/C++ Standards require that the char type be represented in at least 8 bits. Computers supporting less than 8-bits were still being used in the early 80s (e.g., the much beloved ICL 1900 supported 6-bit characters). The C Standard also requires that char be the smallest unit of addressable storage, which means that it must be possible for a pointer to point at an object having a char type.
Designing a processor where the smallest unit of storage is greater than 8-bits but not a power-of-2 is likely to substantially increase all sorts of costs and complicate things enormously (e.g., interfaces to main memory which are designed to work with power of two interfaces). The purpose of this design is to increase other people’s cost, not the proprietary vendor’s cost.
What about that pointer requirement? Perhaps the smallest unit of storage that a pointer could address might be 16 or 40 bits? Such processors exist and compiler writers have used both solutions to the problems they present. One solution is for a pointer to contain the address of the storage location + offset of the byte within that storage (Cray used this approach on a processor whose pointers could only point at 64-bit chunks of storage, with the compiler generating the code to extract the appropriate byte), the other is to declare that the char type occupies 40-bits (several DSP compilers have taken this approach).
Having the compiler declare that char is not 8-bits wide would cause all sorts of grief, so lets not go there. What about the Cray compiler approach?
Some of the address bits on 64-bit processors are not used yet (because few customers need that amount of storage) so compiler writers could get around host-processor pointers not supporting the granularity needed to point at 8-bit objects by storing the extra information in ‘unused’ pointer bits (the compiler generating the appropriate insertion and extraction code). The end result is that the compiler can hide pointer addressability issues :-).
Monte Carlo arithmetic operations
Working out whether software based calculations involving floating-point values delivers a sensible answer requires lots of mathematical sophistication and in practice is often impractical or intractable. The vast majority of developers make no effort, indeed most don’t even know why the effort is needed. Various ‘end-user’ solutions have been proposed, e.g., interval arithmetic.
One interesting solution is to perturb the result of floating-point operations and measure the effect on the final answer. Any calculation that is sensitive to small random changes in the result of an operation (there is randomness present in any operation that operates on values that can only be represented to a finite precision) will produce answers that depend on the direction and magnitude of the perturbation. Comparing the answers from several program executions provides a measure of one kind of error present in the calculation.
Monte Carlo arithmetic is a proposed extension of floating-point arithmetic that operates by randomly selecting how round-off errors occur (the proposer provides sample code).
With computing power continuing to increase, running a program several times is often a viable option (we don’t all number crunch for cpu days). Most of the transistors on a modern CPU chip are devoted to memory cache, using a few of these to support Monte Carlo arithmetic instructions is entirely practical. Perhaps when vendors get over supporting the base-10 radix required by the latest IEEE 754R standard and are looking for something new to attract customers they will provide a mechanism that makes it practical to obtain estimates of some of the error in floating-point calculations.
Will IEEE 754 become a fringe representation?
Many people believe that with a few historical exceptions the IEEE 754 standard has won the floating-point value bit-representation battle. What these people have forgotten is that money rules; customers are willing to ditch standards if it increases profit. FPGA devices can be configured to perform float-point operations faster and more cheaply than commodity cpus.
Making optimal use of a FPGA may require using a radix of 4 and for the time being automatically convert back and forth between an external 754 radix-2 representation. In those cases where multiplication/division operations are more common than addition/subtraction use of a logarithmic number system has performance benefits. For specialist scientific calculations (where cpu time is measured in days) purpose built FPGA devices are the path to significant performance improvements. In many mass market applications the full power of a 32-bit representation is not needed and a representation using fewer bits does an acceptable job using less powerful (ie, cheaper) hardware.
Customer demand for higher performance and lower cost will push vendors to deliver purpose designed products. IEEE 754 may be the floating-point representation that people without spending power use because it was once designed into cpus and vendors are forced to continue to support it for backwards compatibility.
Does the Climategate code produce reliable output?
The source of several rather important commercial programs have been made public recently, or to be more exact programs whose output is important (i.e., the Sequoia voting system and code and data from the Climate Research Unit at University of East Anglia the so called ‘Climategate’ leak). While many technical commentators have expressed amazement at how amateurish the programming appears to be, apparently written with little knowledge of good software engineering practices or knowledge of the programming language being used, those who work on commercial projects know that low levels of software engineering/programming competence is the norm.
The emails included in the Climategate leak provide another vivid example, if one were needed, of why scientific data should be made publicly available; scientists are human and are sometimes willing to hide data that does not fit their pet theory or even fails to validate their theory at all.
The Climategate source has only only recently become available and existing technical commentary has been derived from embarassing comments and the usual complaint about not using the right programming language (Fortran is actually a good choice of language for this problem, it is widely used by climatology researchers and a non-professional programmer is probably makes best of their time by using the one language they know tolerably well rather than attempting to use a new language that nobody else in the research group knows).
An important quality indicator of the leaked software was what was not there, test cases (at least I could not find any). How do we know that a program’s output is correct? One way to gain some confidence in a program’s correctness is to process data for which the correct output is known. This blindness to the importance of program level correctness testing is something that I often encounter in people who are subject area experts rather than professional programmers; they believe that if the output has the form they are expecting it must be correct and will sometimes add ‘faults’ to ‘fix’ output that deviates from what they are expecting.
A quick visual scan through the source showed a tale of two worlds, one of single letter identifier names and liberal use of goto, and the other of what looks like meaningful names, structured code and a non-trivial number of comments. The individuals who have contributed to the code base obviously have very different levels of coding ability. Not having written any Fortran in anger for over 15 years my ability to estimate the impact of more subtle coding practices has atrophied.
What kind of faults might a code review look for in these programs? Common coding errors such as using uninitialized variables and incorrect argument passing are obvious choices and their are tools available to check for these kinds of error. A much more insidious kind of error, which requires people with the mathematical expertise to spot, is created by the approximate nature of floating-point arithmetic.
The source is not huge, but not small either, consisting of around 64,000 lines of Fortran and 16,000 lines of IDL (a language designed for interactive data analysis which to my untrained eye looks a lot like MATLAB). There was no obvious support for building the source included within the leaked files (e.g., no makefiles) and my attempt to manually compile using the GNU Fortran compiler failed miserably. So I cannot say anything reliable about the compiler output warnings.
To me the complete lack of test cases implies that the Climategate code does not produce reliable output. Comments in the code such as
***** APPLIES A VERY ARTIFICIAL CORRECTION FOR DECLINE*********suggests that the authors were willing to patch the code to produce output that matched their expectations; this is the mentality of somebody for whom code correctness is not an important issue and if they don’t believe their code is correct then I don’t either.Source code in itself is rarely that important, although it might have been expensive to create. The real important information in the leaked files is the climate data. Now that this is available others can apply their analysis skills to provide an interpretation to what, if anything statistically reliable, it is telling us.