Archive
Will incorrect answers be biased towards one arm of an if-statement?
Sometimes it is possible to deduce which arm of a nested if-statement will be executed by looking at the form of the conditional expression in the outer if-statement, as in:
if ((L < M) && (M < H)) if (L < H) ; // Execution always end up here else ; // dead code |
but not in:
if ((L > M) && (M < H)) if (L < H) ; // Could end up here else ; // or here |
I ran an experiment at the 2012 ACCU conference where subjects saw nested if-statements like those above and had to specify which arm of the nested if-statement would be executed.
Sometimes subjects gave an answer specifying one arm when in fact both arms are possible. Now dear reader, do you think these incorrect answers will specify the then arm 50% of the time and the else arm 50% or do you think that that incorrect answers will more often specify one particular arm?
Of course I should have thought about this before I started to analyse the data, but this question is unrelated to the subject of the experiment and has only just cropped up because of the unexpectedly high percentage of this kind of incorrect answer. I had an idea what the answer would be but did not stop and think about relative percentages, rushing off to write a few lines of code to print the actual totals, so now my mind is polluted by knowing the answer (well at least for one group of subjects in one experiment).
Why does this “one arm preference” issue matter? The Bayesians out there will insist that the expected distribution (the prior in Bayesian terminology) of incorrectly chosen arms be factored in to the calculation of the probability of getting the numbers seen in the results. The paper Belgian euro coins: 140 heads in 250 tosses – suspicious? gives a succinct summary of the possibilities.
So I have decided to appeal to my experienced readership, yes YOU!
For those questions where the actual execution cannot be predicted in advance, from knowledge of the relative values of variables appearing in the outer if-statement, when an incorrect answer is given should the analysis assume:
- a 50/50 split of incorrect answers between each arm, or
- subjects are more likely to pick one arm; please specify a percentage breakdown between arms.
No pressure, but the submission deadline is very late tomorrow.
The results from the whole experiment will get written up here in future posts.
Update (three days later): Nobody was willing to stick their head above the parapet 🙁
There were 69 correct answers and 16 incorrect answers to questions whose answer was “both arm”. Ten of those incorrect answers specified the ‘then’ arm and 6 the ‘else’; my gut feeling was that there should be even more ‘then’ answers. If there was no “first arm” there is an equal probability of a subject’s incorrect answer appearing in either arm; in this case the probability of a 10/6 split is 12% (so my gut feeling was just hunger pangs after all).
Agreement between code readability ratings given by students
I have previously written about how we know nothing about code readability and questioned how the information content of expressions might be calculated. Buse and Weimer ran a very interesting experiment that asked subjects to rate short code snippets for readability (somebody please rerun this experiment using professional software developers).
I’m interested in measuring how well different students subjects agree with each other (I have briefly written about this before).
Short answer: Very little agreement between individual pairs, good agreement between rankings aggregated by year.
The longer answer is below as another draft section from my book Empirical software engineering with R book. As always comments welcome. R code and data here.
Readability
Source code is often said to have an attribute known as
A study by Buse and Weimer <book Buse_08> asked Computer Science students to rate short snippets of Java source code on a scale of 1 to 5. Buse and Weimer then searched for correlations between these ratings and various source code attributes they obtained by measuring the snippets.
Humans hold diverse opinions, have fragmented knowledge and beliefs about many topics and vary in their cognitive abilities. Any study involving human evaluation that uses an open ended problem on which subjects have had little experience is likely to see a wide range of responses.
Readability is a very nebulous term and students are unlikely to have had much experience working with source code. A wide range of responses is to be expected and the analysis performed here aims to check the degree of readability rating agreement between the subjects.
Data
The data made available by Buse and Weimer are the ratings, on a scale of 1 to 5, given by 121 students to 100 snippets of source code. The student subjects were drawn from those taking first, second and third/fourth year Computer Science degree courses and postgraduates at the researchers’ University (17, 65, 31 and 8 subjects respectively).
The postgraduate data was not used in this analysis because of the small number of subjects.
The source of the code snippets is also available but not used in this analysis.
Is the data believable?
The subjects were not given any instructions on how to rate the code snippets for readability. Also we don’t know what outcome they were trying to achieve when rating, e.g., where they rating on the basis of how readable they personally found the snippets to be, or rating on the basis of the answer they would expect to give if they were being tested in an exam.
The subjects were students who are learning about software development and many of them are unlikely to have had any significant development experience outside of the teaching environment. Experience shows that students vary significantly in their ability to read and write source code and a non-trivial percentage do not go on to become software developers.
Because the subjects are at an early stage of learning about code it is to be expected that their opinions about readability will change while they are rating the 100 snippets. The study did not include multiple copies of some snippets, this would have enabled the consistency of individual subject responses to be estimated.
The results of many studies <book Annett_02> has shown that most subject ratings are based on an ordinal scale (i.e., there is no fixed relationship between the difference between a rating of 2 and 3 and a rating of 3 and 4), that some subjects are be overly generous or miserly in their rating and that without strict rating guidelines different subjects apply different criteria when making their judgements (which can result a subject providing a list of ratings that is inconsistent with every other subject).
Readability is one of those terms that developers use without having much idea what they and others are really referring to. The data from this study can at most be regarded as treating readability to be whatever each subject judges it to be.
Predictions made in advance
Is the readability rating given to code snippets consistent between different students on a computer science course?
The hypothesis is that the between student consistency of the readability rating given to code snippets improves as students progress through the years of attending computer science courses.
Applicable techniques
There are a variety of techniques for estimating rater agreement. <Krippendorff’s alpha> can be applied to ordinal ratings given by two or more raters and is used here.
Subjects do not have to give the same rating to share some degree of consistent response. Two subjects may share a similar pattern of increasing/decreasing/stay the same ratings across snippets. The <Spearman rank correlation> coefficient can be used to measure the correlation between the rank (i.e., relative value within sequence) of two sequences.
Results
When creating the snippets the researchers had no method of estimating what rating subjects would give to them and so there is no reason to expect a uniform distribution of rating values or any other kind of distribution of rating values.
The figure below is a boxplot of the rating of the first 50 code snippets rated by second year students and suggests that many subject ratings are within ±1 of each other.
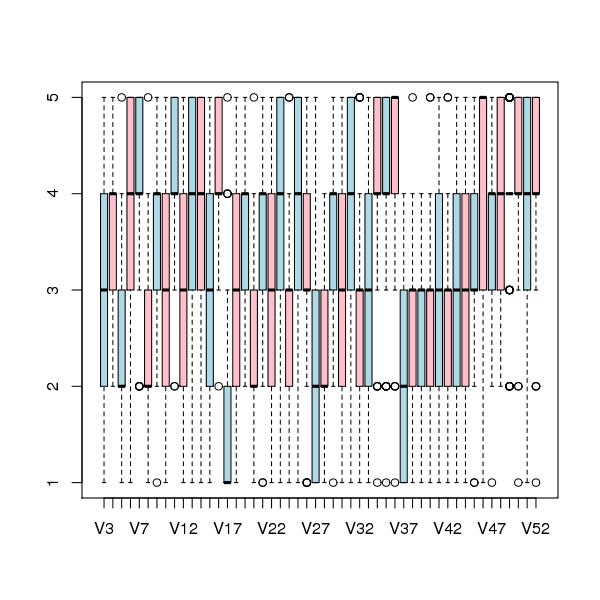
Figure 1. Boxplot of ratings given to snippets 1 to 50 by second year students (colors used to help distinguish boxplots for each snippet).
Between subject rating agreement
The Krippendorff alpha and mean Spearman rank correlation coefficient (the coefficient is calculated for every pair of subjects and the mean value taken) was obtained using the kripp.alpha and meanrho functions from the irr package (a <Jackknife> was used to obtain the following 95% confidence bounds):
Krippendorff's alpha cs1: 0.1225897 0.1483692 cs2: 0.2768906 0.2865904 cs4: 0.3245399 0.3405599 mean Spearman's rho cs1: 0.1844359 0.2167592 cs2: 0.3305273 0.3406769 cs4: 0.3651752 0.3813630 |
Taken as a whole there is a little of agreement. Perhaps there is greater consensus on the readability rating for a subset of the snippets. Recalculating using only using those snippets whose rated readability across all subjects, by year, has a standard deviation less than 1 (around 22, 51 and 62% of snippets respectively) shows some improvement in agreement:
Krippendorff's alpha cs1: 0.2139179 0.2493418 cs2: 0.3706919 0.3826060 cs4: 0.4386240 0.4542783 mean Spearman's rho cs1: 0.3033275 0.3485862 cs2: 0.4312944 0.4443740 cs4: 0.4868830 0.5034737 |
Between years comparison of ratings
The ratings from individual subjects is only available for one of their years at University. Aggregating the answers from all subjects in each year is one method of obtaining readability information that can be used to compare the opinions of students in different years.
How can subject ratings be aggregated to rank the 100 code snippets in order of what a combined group consider to be readability? The relatively large variation in mean value of the snippet ratings across subjects would result in wide confidence bounds for an aggregate based on ratings. Mapping each subject’s rating to a ranking removes the uncertainty caused by differences in mean subject ratings.
With 100 snippets assigned a rating between 1 and 5 by each subject there are going to be a lot of tied rankings. If, say, a subject gave 10 snippets a rating of 5 the procedure used is to assign them all the rank that is the mean of the ranks the 10 of them would have occupied if their ratings had been very slightly different, i.e., (1+2+3+4+5+6+7+8+9+10)/10 = 5.5. This process maps each students readability ratings to readability rankings, the next step is to aggregate these individual rankings.
The R_package[RankAggreg] package contains a variety of functions for aggregating a collection rankings to obtain a group ranking. However, these functions use the relative order of items in a vector to denote rank, and this form of data representations prevents them supporting ranked lists containing items having the same rank.
For this analysis a simple aggregate ranking algorithm using Borda’s method <book lin_10> was implemented. Borda’s method for creating an aggregate ranking operates on one item at a time, combining all of the subject ranks for that item into a single rank. Methods for combining ranks include taking their mean, their geometric mean and the square-root of the sum of their squares; the mean value was used for this analysis.
An aggregate ranking was created for subjects in years one, two and four and the plot below compares the ranking between 1st/2nd year students (left) and 2nd/4th year students (right). The order of the second year student snippet rankings have been sorted and the other year rankings for the snippets mapped to the corresponding position.
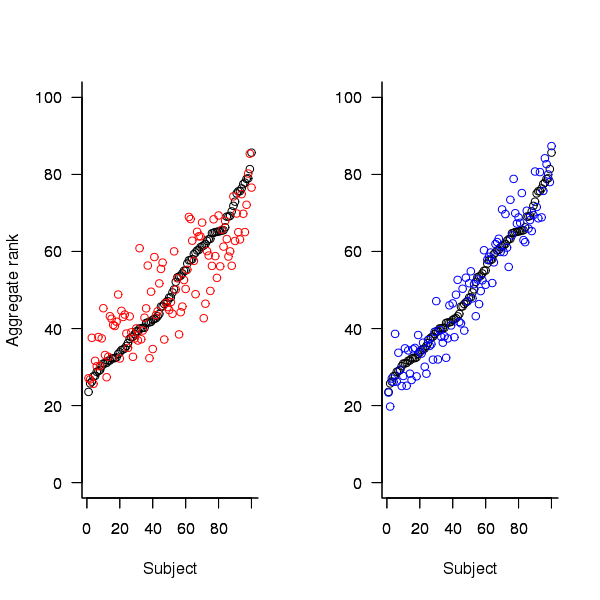
Figure 2. Aggregated ranking of snippets by subjects in years 1 and 2 (red and black) and years 2 and 4 (black and blue). Snippets have been sorted by year 2 ranking.
The above plot seems to show that at the aggregated year level there is much greater agreement between the 2nd/4th years than any other year pairing and measuring the correlation between each of the years using <Kendall’s tau>:
cs1.tau cs2.tau cs3.tau 0.6627602 0.6337914 0.8199636 |
confirms the greater agreement between this aggregate year pair.
Individual subject correlation to year aggregate ranking
To what extend to subject ratings correlate with their corresponding year aggregate? The following plot gives the correlation, using Kendall’s tau, between each subject and their corresponding year aggregate ranking.
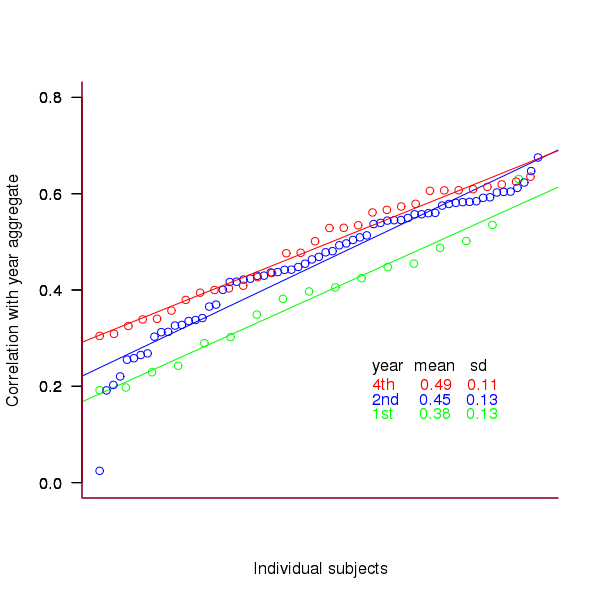
Figure 3. Correlation, using Kendall’s tau, between each subject and their corresponding year aggregate ranking.
The least squares fit shows that the variation in correlation across subjects in any year is very similar (removal of outliers in year 2 would make the lines almost parallel); the mean again shows a correlation that increases with year.
Discussion
The extent to which this study’s calculated values of rater agreement and correlation are considered worthy of further attention depends on the use to which the results will be put.
- From the perspective of trained raters the subject agreement in this study is very low and the rating have no further use.
- From the research perspective the results show that the concept of readability in the computer science student population has some non-zero substance to it that might be worth further study.
- From an overall perspective this study provides empirical evidence for a general lack of consensus on what constitutes readability.
It is not surprising that there is little agreement between student subjects on their readability rating, they are unlikely to have had much experience reading code and have not had any training in rating code for readability.
Professional developers will have spent years working with code and this experience is likely to have resulted in the creation of stable opinions on code readability. While developers usually work with code that is much longer than the few lines contained in the snippets used by Buse and Weimer, this experiment format is easy to administer and supports a fine level of control, i.e., allows a small set of source attributes of interest to be presented while excluding those not of interest. Repeating this study using such people as subjects would show whether this experience results in convergence to general agreement on the readability rating of code.
Summary of findings
The agreement between students readability ratings, for short snippets of code, improves as the students progress through course years 1 to 4 of a computer science degree.
While there is very good aggregated group agreement on the relative ranking of the readability of code snippets there is very little agreement between pairs of individuals.
- Two students chosen at random from within a year will have a low Spearman rank correlation coefficient for their rating of code snippet readability.
- Taken as a yearly aggregate there is a high degree of agreement between years two and four and less, but still good agreement between year 1 and other years.
- There is a broad range of correlations, from poor to good, between year aggregates and student subjects in the corresponding year.
Impact of hardware characteristics on detectable fault behavior
Preface. This is the first of what I hope will be many posts analysing experimental data, that will eventually end up in my empirical software engineering with R book (this experiment was chosen because it happens to be the one I am currently working on; having just switched to using Asciidoc I have a backlog of editing to do on previously written analysis, also I have to figure out a way to fix [bracketed words]).
Don’t worry if you don’t know anything about the statistics used. I am aiming to provide information to meet the needs of two audiences (whether or not I fail on both counts remains to be seen):
- Those who want to some idea of what facts are known about a particular software engineering topic. Hopefully reading the introduction+conclusion will enable these readers to form an opinion about the current state of knowledge (taking my statistical analysis on trust).
- Those who are looking for ideas that can be used to analyse a problem they are trying to solve. Hopefully, somewhere among my many analyses will be something that looks like it could be applied to the reader’s problem and motivates them to go off and learn something about the statistics (if they are not already familiar with it; once written the book will obviously help out here).
Forward. The following analysis produces a negative result, something that happens a lot in experiments in all fields of research. It has been included to illustrate the importance of checking the statistical power of an experiment, i.e., how likely the experiment will detect an effect if one is present; it is very easy to fall into the trap of thinking that because lots of tests were done any effect that exists will be detected.
The authors ran an interesting experiment which as far as I know is the only published empirical analysis of intermittent software faults (please let me know if you are aware of other work) and made some mistakes in their statistical analysis. I have made plenty of mistakes in experiments I have run, some of which have found there way into the published write up. The key attribute of an experimentalist is to learn and move on.
A fault does not always noticeably change the behavior of a program when it is executed, apparently correct program execution can occur in the presence of serious faults.
A study by Syed, Robinson and Williams <book Syed_10> investigated how the number of noticeable failures caused by known faults in Mozilla’s Firefox browser varied with processor speed, system memory, hard disc size and system load. A total of 11 known faults causing intermittent failure were selected and nine different hardware configurations were selected. The conditions required to exhibit each fault were replicated and Firefox was executed 10 times for each of hardware configuration, counting the number of noticeable program failures; the seven faults and nine hardware configurations listed in the table below generated a total of 10*7*9 = 630 different executions (four faults either always or never resulted in an observed failure during the 10 runs).
Data
The following table contains the observed number of failures of Firefox for the given fault number when run on the specified hardware configuration.
| Mhz-Mb-Gb | 124750 | 380417 | 410075 | 396863 | 494116 | 264562 | 332330 |
|---|---|---|---|---|---|---|---|
|
667-128-2.5 |
4 |
10 |
6 |
5 |
2 |
3 |
5 |
|
667-256-10 |
4 |
8 |
8 |
6 |
4 |
3 |
8 |
|
667-1000-2.5 |
4 |
7 |
3 |
4 |
3 |
1 |
8 |
|
1000-128-10 |
3 |
10 |
3 |
6 |
0 |
1 |
1 |
|
1000-256-2.5 |
3 |
9 |
0 |
6 |
0 |
1 |
2 |
|
1000-1000-10 |
2 |
9 |
4 |
5 |
0 |
0 |
1 |
|
2000-128-2.5 |
0 |
10 |
5 |
6 |
0 |
0 |
0 |
|
2000-256-10 |
2 |
8 |
5 |
7 |
0 |
0 |
0 |
|
2000-1000-10 |
1 |
7 |
3 |
5 |
0 |
0 |
0 |
Predictions made in advance
There is no prior theory suggesting how the selected hardware characteristics might influence the outcome from this experiment. The analysis is based on searching for a pattern in the results and so the significance level needs to be adjusted to take account of the number of possible patterns that could exist (e.g., using the [Bonferroni correction]).
If we simplify the failure counts by labelling them as one of Low/Medium/High, then there are two arrangements of the failure counts (i.e., low/medium/high and high/medium/low) that would result in a strong correlation for cpu_speed, two arrangements for memory and two for disc size; a total of 6 combinations that would result in a strong correlation being found.
The [Bonferroni correction] adjusts the significance level by dividing by the number of tests, in this case 0.05/6 = 0.0083.
If the failure counts occurred in a random order what is the probability of a strong correlation between failure count and one of the hardware attributes being found? Based on the Low/Medium/High labelling scheme there are 9!/(3! 3! 3!) = 1680 combinations of these counts over 9 slots, giving a 1 in 1680/6 = 280 chance of purely random behavior producing a strong correlation.
The experiment investigated the characteristics of 11 faults. If there is a 1 in 280 chance of finding a strong correlation when analyzing one fault there is approximately a 1 in 24 chance of finding at least one strong correlation when analysing 11 different faults.
Response variable
The response variable takes the form of a proportion whose value varies between 0 and 1, the number of failures out of 10 executions.
Applicable techniques
The following techniques might be used to analyse this data:
- [Factorial design]. This is a way of organizing experiment configurations that is designed to extract the most information for the total number of program runs made. It would be inefficient not to use the results from some hardware configurations just because they are not needed in the factorial design and no results are available for some configurations required by a factorial design (or a [Plackett-Burman] design).
-
Fitting the data using a linear model. A standard linear model, created using R’s lm function, would not be appropriate because of the following two problems:
- this kind of model is likely to make predictions that fall outside the range 0 to 1, something that cannot happen for proportional data,
- this approach assumes that the variance is constant across measurements and unless the proportions involved are very close to each other this requirement will not be met ([proportional data] from a [binomial distribution] has variance p(1-p)).
However, a generalised linear model would not suffer from these problems. There are several [link functions] that could be used:
- the Poisson distribution, is widely used for modelling faults but requires that the mean and variance have the same value, a property that does not apply to proportional data.
- the Binomial distribution, can handle data having the characteristics present here.
The proportional data is specified in the call to the glm function by having the response variable contain two columns, one containing the number of failures (that is what is being predicted in this case) and the other the number of non-failures. The code looks something like the following (see complete example and data):
y=cbind(fail_count, 10-fail_count) glm(y ~ cpu_speed+memory+disk_size, data=ff_data, family=binomial) |
In this kind of GLM it is assumed that the [residual deviance] is the same as the [residual degrees of freedom]. If the residual deviance is greater than the residual degrees of freedom then [overdispersion] has occurred, which happens for fault 380417. To handle overdispersion the family needs to be changed from binomial to quasibinomial, which in the case of fault 380417 changes the p-value of the fit from 0.0348 to 0.0749.
The analysis of each fault finds that only one of them, 332330, has a significance level within the specified acceptable bounds; this has a negative correlation with CPU speed (i.e., observed failures decrease with clock speed).
With only one faults found to have any significant hardware configuration effects we have to ask about the probability of this experiment finding an effect if one was present.
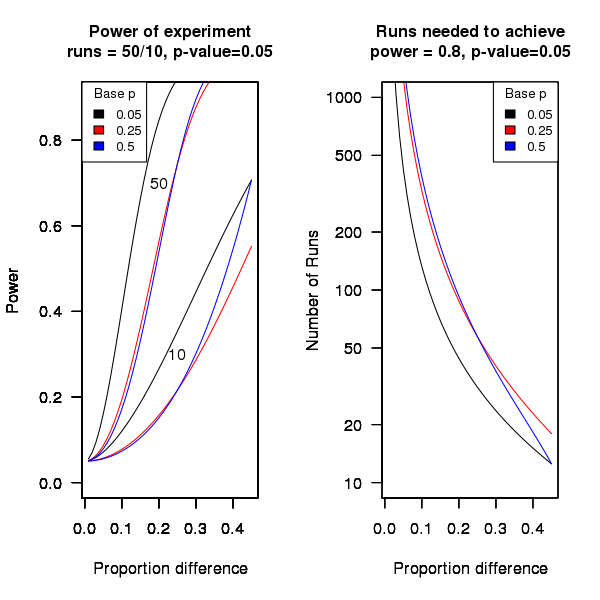
An analysis of the [statistical power] of an experiment investigating the difference between proportions for two hardware configurations (i.e., the percentage of observed failures) needs to know the value of those proportions, the number of runs (10 in this case) and the desired p-value (0.05); to simplify things the plot below is based on using the value of the lowest proportion and the difference between it and the higher proportion. The left plot shows the power achieved (y-axis) there does exist a given difference in proportions (x-axis), the three lowest proportions of 0.05, 0.25 and 0.5 are shown (the result is symmetric about 0.5 and so the plot for 0.75 and 0.95 would be the same as 0.25 and 0.05 respectively), and where there were 10 and 50 runs involving the same fault case.
It can be seen that unless a change in the hardware configuration causes a large change in the number of visible failures then the chance of a difference being detected in results from 10 runs is well below 0.5 (i.e., less than a 50% chance of detecting a difference at a p-value of 0.05 or better).
The right plot in the figure gives the number of runs that need to be made to have a 80% chance of detecting, between two different hardware configurations, the difference in proportion listed on the x-axis, at a significance of 0.05.
It can be seen that if hardware charactersitics account for only 10% of the difference in failure rate over 100 runs would be needed to detect it.
Conclusion
Faults in Firefox that caused intermittent failures were investigated looking for a correlation with system cpu speed, memory or disc size. One fault showed a strong correlation with cpu speed (there is a 1 in 24 chance that one of the investigated faults would have some kind of strong correlation). This experiment may not have found a significant correlation between observed failure rate and hardware configuration because the number of separate runs for each fault (i.e., 10) had [low power].
Using identifier prefixes results in more developer errors
Human speech communication has to be processed in real time using a cpu with a very low clock rate (i.e., the human brain whose neurons fire at rates between 10-100 Hz). Biological evolution has mitigated the clock rate problem by producing a brain with parallel processing capabilities and cultural evolution has chipped in by organizing the information content of languages to take account of the brains strengths and weaknesses. Words provide a good example of the way information content can be structured to be handled by a very slow processor/memory system, e.g., 85% of English words start with a strong syllable (for more details search for initial in this detailed analysis of human word processing).
Given that the start of a word plays an important role as an information retrieval key we would expect the code reading performance of software developers to be affected by whether the identifiers they see all start with the same letter sequence or all started with different letter sequences. For instance, developers would be expected to make fewer errors or work quicker when reading the visually contiguous sequence consoleStr, startStr, memoryStr and lineStr, compared to say strConsole, strStart, strMemory and strLine.
An experiment I ran at the 2011 ACCU conference provided the first empirical evidence of the letter prefix effect that I am aware of. Subjects were asked to remember a list of four assignment statements, each having the form id=constant;, perform an unrelated task for a short period of time and then recall information about the previously seen constants (e.g., their value and which variable they were assigned to).
During recall subjects saw a list of five identifiers and one of the questions asked was which identifier was not in the previously seen list? When the list of identifiers started with different letters (e.g., cat, mat, hat, pat and bat) the error rate was 2.6% and when the identifiers all started with the same letter (e.g., pin, pat, pod, peg, and pen) the error rate was 5.9% (the standard deviation was 4.5% and 6.8% respectively, but ANOVA p-value was 0.038). Having identifiers share the same initial letter appears to double the error rate.
This looks like great news; empirical evidence of software developer behavior following the predictions of a model of human human speech/reading processing. A similar experiment was run in 2006, this asked subjects to remember a list of three assignment statements and they had to select the ‘not seen’ identifier from a list of four possibilities. An analysis of the results did not find any statistically significant difference in performance for the same/different first letter manipulation.
The 2011/2006 experiments throw up lots of questions, including: does the sharing a prefix only make a difference to performance when there are four or more identifiers, how does the error rate change as the number of identifiers increases, how does the error rate change as the number of letters in the identifier change, would the effect be seen for a list of three identifiers if there was a longer period between seeing the information and having to recall it, would the effect be greater if the shared prefix contained more than one letter?
Don’t expect answers to appear quickly. Experimenting using people as subjects is a slow, labour intensive process and software developers don’t always answer the question that you think they are answering. If anybody is interested in replicating the 2011 experiment the tools needed to generate the question sheets are available for download.
For many years I have strongly recommended that developers don’t prefix a set of identifiers sharing some attribute with a common letter sequence (its great to finally have some experimental backup, however small). If it is considered important that an attribute be visible in an identifiers spelling put it at the end of the identifier.
See you all at the ACCU conference tomorrow and don’t forget to bring a pen/pencil. I have only printed 40 experiment booklets, first come first served.
Randomizing a list of items using sort() and rand()
I’m busy putting together the experiment I will be running at the ACCU conference next week. If you are attending the conference please reserve your Thursday lunchtime slot for taking part as a subject!
Experiment generation invariably involves randomizing the sequence of items seen by every subject. While few languages support a randomise function many support sorting and random number generation. These two functions can be combined to create a randomize function; simply append a random number to the start of each item, sort it and then strip off the random number. Voilà a randomized list (awk code below).
function rand_items(items) { for (v in items) { items[v]=rand() " " items[v] } asort(items) for (v in items) { sp_pos=index(items[v], " ") items[v]=substr(items[v], sp_pos+1) } } |
This randomization problem is not yet listed on Rosetta code and probably has longer solutions in other languages.
Update (the next day).
The glow I have had for the last 10 years over coming up with a neat solution to a problem has now disappeared. Following the link kindly provided by D. Herring in the comments eventually lead me to the Fisher-Yates shuffle, which has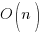 
performance (the call to sort is probably 
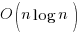. The following shuffles a deck of cards:
for (i = 0; i < 52; i++) { j = i + (rand() % (52 - i)); tmp = card[i]; card[i] = card[j]; card[j] = tmp; } |
The proof of the uniform shuffling behavior of Fisher-Yates (also known as Knuth shuffle) is straight forward but not nearly as appealing as using rand and sort.
Correlation between risk attitude and willingness to refer back
What is the connection between a software developer’s risk attitude and the faults they insert in code they write or fail to detect in code they review? This is a very complicated question and in an experiment performed at the 2011 ACCU conference I investigated one particular instance; the connection between risk attitude and recall of previously seen information.
The experiment consisted of a series of problems having the same format (the identifiers used varied between problems). Each problem involved remembering information on four assignment statements of the form:
p = 6 ; b = 4 ; r = 9 ; k = 8 ; |
performing some other unrelated task for a short time (hopefully long enough for them to forget some of the information they had previously seen) and then having to recognize the variables they had previously seen within a list containing five identifiers and recall the numeric value assigned to each variable.
When reading code developers have the option of referring back to previously read code and this option was provided to subject. Next to each identifier listed in the recall part of the problem was space to write the numeric value previously seen and a “would refer back” box. Subjects were told to tick the “would refer back” box if, in real life” they would refer back to the previously seen assignment statements rather than rely on their memory.
As originally conceived this experimental format is investigating the impact of human short term memory on recall of previously seen code. Every time I ran this kind of experiment there was a small number of subjects who gave a much higher percentage of “would refer back” answers than the other subjects. One explanation was that these subjects had a smaller short term memory capacity than other subjects (STM capacity does vary between people), another explanation is that these subjects are much more risk averse than the other subjects.
The 2011 ACCU experiment was designed to test the hypothesis that there was a correlation between a subject’s risk attitude and the percentage of “would refer back” answers they gave. The Domain-Specific Risk-Taking (DOSPERT) questionnaire was used to measure subject’s risk attitude. This questionnaire and the experimental findings behind it have been published and are freely available for others to use. DOSPERT measures risk attitude in six domains: social, recreation, gambling, investing health and ethical.
The following scatter plot shows each (of 30) subject’s risk attitude in the six domains (x-axis) plotted against percentage of “would refer back” answers (y-axis).
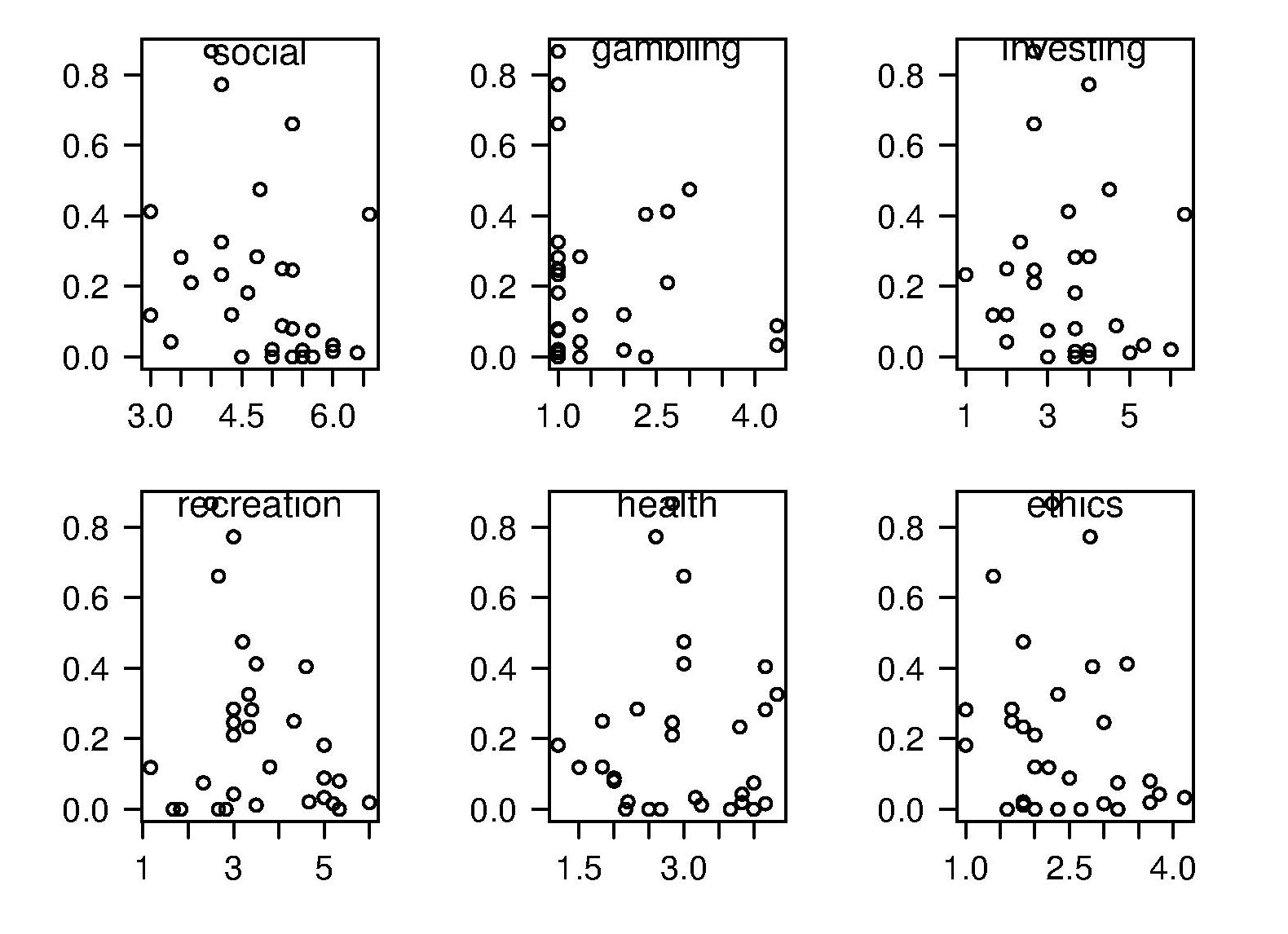
A Spearman rank correlation test confirms what is visibly apparent, there is no correlation between the two quantities. Scatter plots using percentage of correct answers and total number of questions answers show a similar lack of correlation.
The results suggest that risk attitude (at least as measured by DOSPERT) is not a measurable factor in subject recall performance. Perhaps the subjects that originally caught my attention (there were three in 2011) really do have a smaller STM capacity compared to other subjects. The organization of the experiment (one hour during a one lunchtime of the conference) does not allow for a more extensive testing of subject cognitive characteristics.
Empirical software engineering is five years old
Science and engineering are built on theoretical models that are tested against measurements of ‘reality’. Until around 10 years ago there was very little software engineering ‘reality’ publicly available; companies rarely made source available and were generally unforthcoming about any bugs that had been discovered. What happened around 10 years ago was the creation of public software repositories such as SourceForge and public fault databases such as Bugzilla. At last researchers had access to what could be claimed to be real world data.
Over the last five years there has been an explosion of papers using SourceForge/Bugzilla kinds of data looking for a connection between everything+kitchen sink and faults. The traditional measures such as Halstead and McCabe have not stood up well against this onslaught of data, hardly surprising given they were more or less conjured out of thin air. Some researchers are trying to extract information about developer characteristics from mailing lists; given that software is written by developers there is obviously a real need for the characteristics of major project contributors to play a significant role in any theory of software faults.
Software engineering data includes a lot more than what can be extracted from source code, bug lists and email lists. A growing number of repositories have been set up to hold measurement and experimental data, e.g., hardware failures, effort prediction (while some of this data is pre-2000 it tends to be low volume or poor quality), and file system related.
At the individual level a small number of researchers have made data available on their own web site, a few more will send a copy if asked and sadly there are many cases where the raw data has been lost. In two recent cases researchers have responded to my request for raw data by telling me they are working on additional papers and don’t want to make the data public yet. I can understand that obtaining interesting data requires a lot of work and researchers want to extract maximum benefit; I look forward to see the new papers and the eventual availability of the data.
My interest in all this data is that I have started work on a book covering empirical software engineering using R. Five years ago such book would have contained lots of equations, plenty of hand waving and if data sets were available they would probably have been small enough to print on one page. Today there are still plenty of equations (mostly relating to statistical this that and the other), no hand waving (well, none planned), data sets for everything covered (some in the gigabytes and a few that can still fit on a page) and pretty pictures (color graphs, as least for the pdf version).
When historians trace back the history of empirical software engineering I think they will say that it started for real sometime around 2005. Before then, any theories that were based on observation tended to have small, single study, data sets with little statistical significance or power.
The complexity of three assignment statements
Once I got into researching my book on C I was surprised at how few experiments had been run using professional software developers. I knew a number of people on the Association of C and C++ Users committee, in particular the then chair Francis Glassborow, and suggested that they ought to let me run an experiment at the 2003 ACCU conference. They agreed and I have been running an experiment every year since.
Before the 2003 conference I had never run an experiment that had people as subjects. I knew that if I wanted to obtain a meaningful result the number of factors that could vary had to be limited to as few as possible. I picked a topic which has probably been the subject of more experiments that any other topics, short term memory. The experimental design asked subjects to remember a list of three assignment statements (e.g., X = 5;), perform an unrelated task that was likely to occupy them for 10 seconds or so, and then recognize the variables they had previously seen within a list and recall the numeric value assigned to each variable.
I knew all about the factors that influenced memory performance for lists of words: word frequency, word-length, phonological similarity, how chunking was often used to help store/recall information and more. My variable names were carefully chosen to balance all of these effects and the information content of the three assignments required slightly more short term memory storage than subjects were likely to have.
The results showed none of the effects that I was expecting. Had I found evidence that a professional software developer’s brain really did operate differently than other peoples’ or was something wrong with my experiment? I tried again two years later (I ran a non-memory experiment the following year while I mulled over my failure) and this time a chance conversation with one of the subjects after the experiment uncovered one factor I had not controlled for.
Software developers are problem solvers (well at least the good ones are) and I had presented them with a problem; how to remember information that appeared to require more storage than available in their short term memories and accurately recall it shortly afterwards. The obvious solution was to reduce the amount of information that needed to be stored by simply remembering the first letter of every variable (which one of the effects I was controlling for had insured was unique) not the complete variable name.
I ran another experiment the following year and still did not obtain the expected results. What was I missing now? I don’t know and in 2008 I ran a non-memory based experiment. I still have no idea what techniques my subjects are using to remember information about three assignment statements that are preventing me getting the results I expect.
Perhaps those researchers out there that claim to understand the processes involved in comprehending a complete function definition can help me out by explaining the mental processes involved in remembering information about three assignment statements.
Measuring developer coding expertise
A common measure of developer experience is the number of years worked. The only good that can be said about this measure is that it is easy to calculate. Studies of experts in various fields have found that acquiring expertise requires a great deal of deliberate practice (10,000 hours is often quoted at the amount of practice put in by world class experts).
I think that coding expertise is acquired by reading and writing code, but I have little idea of the relative contributions made by reading and writing and whether reading the same code twice count twice or is there a law of diminishing returns on rereading code?
So how much code have developers read and written during their professional lives? Some projects have collected information on the number of ‘delivered’ lines of code written by developers over some time period. How many lines does a developer actually write for every line delivered (some functions may be rewritten several times while others may be deleted without every being making it into a final delivery)? Nobody knows. As for lines of code read, nobody has previously expressed an interest in collecting this kind of information.
Some experiments, involving professional developers, I have run take as their starting point that developer performance improves with practice. Needing some idea of the amount of practice my subjects have had reading and writing code I asked them to tell me how much code they think they have read and written, as well as the number of years they have worked professionally in software development.
The answers given by my subjects were not very convincing:
Estimates of the ratio code read/written varied by more than five to one (the above graph suffers from a saturation problem for lines of code read, I had not provided a tick box that was greater than 250,000). I cannot complain, my subjects volunteered part of their lunch time to take part in an experiment and were asked to answer these questions while being given instructions on what they were being asked to do during the experiment.
I have asked this read/written question a number of times and received answers that exhibit similar amounts of uncertainty and unlikeliness. Thinking about it I’m not sure that giving subjects more time to answer this question would improve the accuracy of the answers. Very few developers monitor their own performance. The only reliable way of answering this question is by monitoring developer’s eye movements as they interact with code for some significant duration of time (preferably weeks).
Unobtrusive eye trackers may not be sufficiently accurate to provide a line-of-code level of resolution and the more accurate head mounted trackers are a bit intrusive. But given their price more discussion on this topic is currently of little value 🙁
Unexpected experimental effects
The only way to find out the factors that effect developers’ source code performance is to carry out experiments where they are the subjects. Developer performance on even simple programming tasks can be effected by a large number of different factors. People are always surprised at the very small number of basic operations I ask developers to perform in the experiments I run. My reply is that only by minimizing the number of factors that might effect performance can I have any degree of certainty that the results for the factors I am interested in are reliable.
Even with what appear to be trivial tasks I am constantly surprised by the factors that need to be controlled. A good example is one of the first experiments I ever ran. I thought it would be a good idea to replicate, using a software development context, a widely studied and reliably replicated human psychological effect; when asked to learn and later recall/recognize a list of words people make mistakes. Psychologists study this problem because it provides a window into the operation structure of the human memory subsystem over short periods of time (of the order of at most tens of seconds). I wanted to find out what sort of mistakes developers would make when asked to remember information about a sequence of simple assignment statements (e.g.,
qbt = 6;).I carefully read the appropriate experimental papers and had created lists of variables that controlled for every significant factor (e.g., number of syllables, frequency of occurrence of the words in current English usage {performance is better for very common words}) and the list of assignment statements was sufficiently long that it would just overload the capacity of short term memory (about 2 seconds worth of sound).
The results contained none of the expected performance effects, so I ran the experiment again looking for different effects; nothing. A chance comment by one of the subjects after taking part in the experiment offered one reason why the expected performance effects had not been seen. By their nature developers are problem solvers and I had set them a problem that asked them to remember information involving a list of assignment statements that appeared to be beyond their short term memory capacity. Problem solvers naturally look for patterns and common cases and the variables in each of my carefully created list of assignment statements could all be distinguished by their first letter. Subjects did not need to remember the complete variable name, they just needed to remember the first letter (something I had not controlled for). Asking around I found that several other subjects had spotted and used the same strategy. My simple experiment was not simple enough!
I was recently reading about an experiment that investigated the factors that motivate developers to comment code. Subjects were given some code and asked to add additional functionality to it. Some subjects were given code containing lots of comments while others were given code containing few comments. The hypothesis was that developers were more likely to create comments in code that already contained lots of comments, and the results seemed to bear this out. However, closer examination of the answers showed that most subjects had cut and pasted chunks (i.e., code and comments) from the code they were given. So code the percentage of code in the problem answered mimicked that in the original code (in some cases subjects had complicated the situation by refactoring the code).