Archive
von Neumann’s deduction that biological reproduction is digital
We now know that the reproduction and growth of organisms is driven by DNA and proteins. The DNA contains the instructions which proteins execute.
If we travelled back in time, what arguments might we use to convince people that ‘our’ model for how organisms reproduced and grew was correct?
The General and Logical Theory of Automata is a talk given in 1948 by John von Neumann, four years before the discovery of the structure of DNA.
In this talk, von Neumann deduces from first principles:
- that the mechanism for organism reproduction must be digitally based, rather than analogue. His argument is based on error rates. The performance of the recently invented computers showed that it was possible for digital systems to return correct results for calculations requiring at least
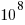operations; while for analogue systems the signal/noise ratio is often 
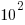, with 
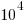to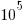 
sometimes being possible.
Prior to 1940s valve based electronic computers, relays were used to build what were essentially digital devices.
Relays go back to the mid-1800s, which is when Boolean algebra was created. The Jacquard weaving loom takes us back to the start of the 1800s, but there is not yet any digital mathematics to cite,
- it is possible for a simple machine to build a much more complicated machine. Twelve years earlier, Turing had published his results around the universal capabilities of a Turing machine, i.e., Turing completeness, the ability of any Turing machine to perform any calculation that any other Turing machine can calculate.
Turing completeness is a surprising result. An argument that it is possible for simple machines to build more complicated, prior to Turin, would have to rely on evidence such as ship building,
- a conceptual algorithm for a self-reproducing machine; this uses two Turing machines, and a mechanism for sequentially controlling operations.
A talk on automata obviously has to say something about organic computers, i.e., the brain. The von Neumann paper intermixes the discussion of neurons and reproduction. McCulloch, of McCulloch & Pitts neurons fame, was in the audience, as was the psychologist Karl Lashley, and neuroscientist Lorente de Nó. The recorded post talk discussion was mostly ‘brain’ oriented.
Source code will soon need to be radiation hardened
I think I have discovered a new kind of program testing that may soon need to be performed by anybody wanting to create ultra-reliable software.
A previous post discussed the compiler related work being done to reduce the probability that a random bit-flip in the memory used by an executing program will result in a change in behavior. At the moment 4G of ram is expected to experience 1 bit-flip every 33 hours due to cosmic rays and the rate of occurrence is likely to increase.
Random corrupts on communications links are protected by various kinds of CRC checks. But these checks don’t catch every corruption, some get through.
Research by Artem Dinaburg looked for, and found, occurrences of bit-flips in domain names appearing within HTTP requests, e.g., a page from the domain ikamai.net being requested rather than from akamai.net. A subsequent analysis of DNS queries to VERISIGN’S name servers found “… that bit-level errors in the network are relatively rare and occur at an expected rate.” (the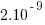 
bit error rate was thought to occur inside routers and switches).
Javascript is the web scripting language supported by all the major web browsers and the source code of JavaScript programs is transmitted, along with the HTML, for requested web pages. The amount of JavaScript source can dwarf the amount of HTML in a web page; measurements from four years ago show users of Facebook, Google maps and gmail receiving 2M bytes of Javascript source when visiting those sites.
If all the checksums involved in TCP/IP transmission are enabled the theoretical error rate is 1 in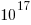 
bits. Which for 1 billion users visiting Facebook on average once per day and downloading 2M of Javascript per visit is an expected bit flip rate of once every 5 days somewhere in the world; not really something to worry about.
There is plenty of evidence that the actual error rate is much higher (because, for instance, some checksums are not always enabled; see papers linked to above). How much worse does the error rate have to get before developers need to start checking that a single bit-flip to the source of their Javascript program does not result in something nasty happening?
What we really need is a way of automatically radiation hardening source code.
What is the error rate for published mathematical proofs?
Mathematical proofs are sometimes cited as the gold standard against which software quality should be compared. At school we rarely get to hear about proofs that turn out to be wrong and are inculcated with the prevailing wisdom that all mathematical proofs are correct.
There are many technical and social issues involved in believing a published proof and well known established mathematicians have no trouble pointing out that “… it is impossible to write out a very long and complicated argument without error, …”
Examples of incorrect published proofs include Wiles’ first proof of Fermat’s Last Theorem and an serious error found in a proof of a message signing scheme.
A question on mathoverflow contains a list of rather interesting false proofs.
Then, of course, there are always those papers that appear in journals that get written about more frequently on Retraction Watch than others.
What is the error rate for published mathematical proofs? I have not been able to find any collection of mathematical proof error data.
Several authors have expressed the view that because there so many diverse mathematical topics being studied these days there are very few domain experts available to check proofs. A complicated proof of a not particularly interesting result is unlikely to attract the attention needed to check it thoroughly. It should come as no surprise that the number of known errors in such proofs is equal to the number of known errors in programs that have never been executed.
Proofs are different from programs in that one error can be enough to ‘kill-off’ a proof, while a program can contain many errors and still be useful. Do errors in programs get talked about more than errors in proofs? I rarely get to socialize with working mathematicians and so cannot make any judgment call on this question.
Every non-trivial program is likely to contain many errors; can the same be said for long mathematical proofs? Are many of these errors as trivial (in the sense that they are easily fixed) as errors in programs?
One commonly used error rate for programs is errors per line of code; how should the rate be expressed for proofs? Errors per page, per line, per definition?
Lots of questions and I’m hoping one of my well informed readers will be able to provide some answers or at least cite a reference that does.
Recent Comments