Archive
Number of statement sequences possible using N if-statements
I recently read a post by Terence Tao describing how he experimented with using ChatGPT to solve a challenging mathematical problem. A few of my posts contain mathematical problems I could not solve; I assumed that solving them was beyond my maths pay grade. Perhaps ChatGPT could help me solve some of them.
To my surprise, a solution was found to the first problem I tried.
I simplified the original problem (involving Motzkin numbers, details below) down to something that was easier for me to explain to ChatGPT. Based on ChatGPT’s response, it appeared lost, so I asked what it knew about Motzkin numbers. I then reframed the question around the concepts in its response, and got a response that, while reasonable, was not a solution. My question was not precise enough, and a couple of question/answer iterations later, ChatGPT broke the problem down into a series of steps that I saw could solve the problem. While the equation it used in its answer was just wrong, I knew what the correct equation was. So while ChatGPT frequently went off in the wrong direction and got its maths wrong, it helped me refine my statement of the problem and ChatGPT eventually gave steps to a solution which were blindingly obvious to me when I read them.
The question I wanted to answer was: How many distinct statement sequences can be created using 
if-statements and  simple-statements (for a total of
simple-statements (for a total of 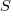 statements)?
statements)?
A simple-statement might be an assignment or function call, but not any kind of compound statement, such as a loop. Three sequences are possible using one if-statement and two simple-statements. The if-statement occupies two lines, i.e., the condition and termination curly-bracket, }, as follows:
s1; if (c1) { if (c1) { if (c1) { s1; s1; s2; s2; } } } s2; |
In a previous post I showed how a variant of this question, involving any number of if-statements, can be mapped to a combinatorial interpretation of Motzkin numbers and treating matching up/down diagonals along a path as an if-statement.

ChatGPT performed poorly when I phrased the problem in combinatorial terms (or perhaps my phrasing was poor), so I switched to using a lattice path approach. I asked: “How many lattice paths of length S containing exactly N occurrences of the step (1, 1) and N occurrences of the step (1, -1) are possible?”, and after reading the response I replied “Your analysis does not take into account the fact that the path cannot go below the x-axis. Rework your analysis to take this restriction into account.”
The following is my edited version of ChatGPT’s ‘solution’ response:
“Problem Restated:
We need to count the number of valid Dyck paths of length 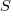 , where the path consists of:
, where the path consists of:
Exactly  upward steps (1,1).
upward steps (1,1).
Exactly  downward steps (1,−1).
downward steps (1,−1).
The remaining steps (which must be  horizontal steps (1,0)).
horizontal steps (1,0)).
These paths must never dip below the x-axis, and they must return to the x-axis at the end.
…
Step 2: Catalan Numbers for Balanced Paths
If we ignore the horizontal steps for the moment, the number of ways to place  upward steps and
upward steps and  downward steps such that the path does not go below the x-axis is given by the Catalan number
downward steps such that the path does not go below the x-axis is given by the Catalan number 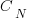 :
:
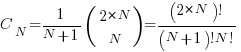
This Catalan number counts the number of valid ways to arrange the  upward steps and
upward steps and  downward steps such that the path remains above or on the x-axis.
downward steps such that the path remains above or on the x-axis.
Step 3: Placing Horizontal Steps
Once the valid upward and downward steps have been arranged in a Catalan structure, we can freely place the  horizontal steps (1,0) in the remaining positions of the path. Since there are
horizontal steps (1,0) in the remaining positions of the path. Since there are 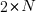 steps (upward and downward) and
steps (upward and downward) and  horizontal steps, there are
horizontal steps, there are 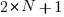 gaps (before, after, or between the upward/downward steps) where the horizontal steps can be placed.
gaps (before, after, or between the upward/downward steps) where the horizontal steps can be placed.
The number of ways to place  horizontal steps in these
horizontal steps in these 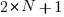 positions is given by a binomial coefficient:”
positions is given by a binomial coefficient:”
For some reason, ChatGPT gives the wrong binomial coefficient. Calculating the number of ways of distributing 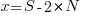 items into
items into 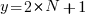 bins is a well known problem; when a bin can contain zero items, the solution is:
bins is a well known problem; when a bin can contain zero items, the solution is: 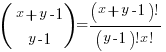 .
.
Combining the equations from the two steps gives the number of distinct statement sequences that can be created using 
if-statements and  simple-statements as:
simple-statements as:
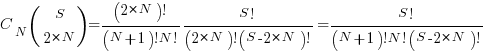
The above answer is technically correct, however, it fails to take into account that in practice an if-statement body will always contain either another if-statement or a simple statement, i.e., the innermost if-statement of any nested sequence cannot be empty (the equation used for distributing items into bins assumes a bin can be empty).
Rather than distributing  statements into
statements into 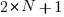 gaps, we first need to insert one simple statement into each of the innermost if-statements. The number of ways of distributing the remaining statements are then counted as previously. How many innermost if-statements can be created using
gaps, we first need to insert one simple statement into each of the innermost if-statements. The number of ways of distributing the remaining statements are then counted as previously. How many innermost if-statements can be created using  if-statements? I found the answer to this question in a StackExchange question, using traditional search.
if-statements? I found the answer to this question in a StackExchange question, using traditional search.
The question can be phrased in terms of peaks in Dyck paths, and the answer is contained in the Narayana numbers (which I had never heard of before). The following example, from Wikipedia, shows the number of paths containing a given number of peaks, that can be produced by four if-statements:
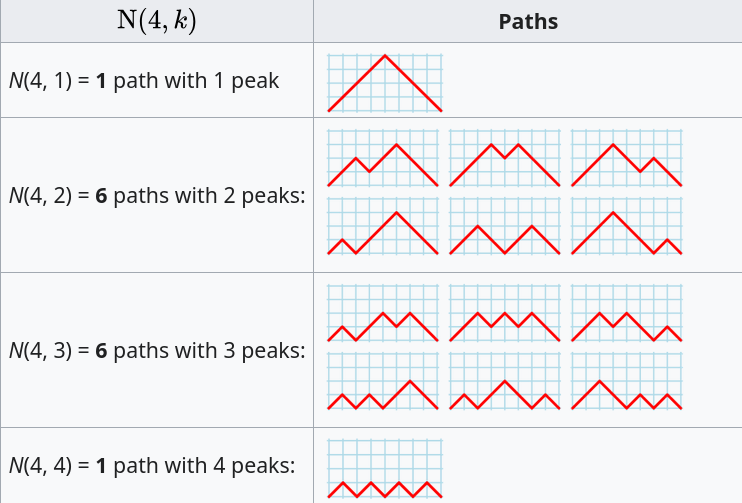
The sum of all these paths is the Catalan number for the given number of if-statements, e.g., using 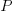 to denote the Narayana number:
to denote the Narayana number: 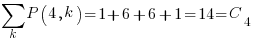 .
.
Adding at least one simple statement to each innermost if-statement changes the equation for the number of statement sequences from 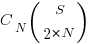 , to:
, to:
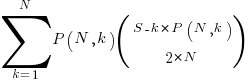
The following table shows the number of distinct statement sequences for five-to-twenty statements containing one-to-five if-statements:
N if-statements
1 2 3 4 5
5 6 1
6 10 6
7 15 20 1
8 21 50 7
9 28 105 29 1
10 36 196 91 9
11 45 336 238 45 1
12 55 540 549 166 11
S 13 66 825 1,155 504 66
14 78 1,210 2,262 1,332 286
15 91 1,716 4,179 3,168 1,002
16 105 2,366 7,351 6,930 3,014
17 120 3,185 12,397 14,157 8,074
18 136 4,200 20,153 27,313 19,734
19 153 5,440 31,720 50,193 44,759
20 171 6,936 48,517 88,458 95,381 |
The following is an R implementation of the calculation:
Narayana=function(n, k) choose(n, k)*choose(n, k-1)/n
Catalan=function(n) choose(2*n, n)/(n+1)
if_stmt_possible=function(S, N)
{
return(Catalan(N)*choose(S, 2*N)) # allow empty innermost if-statement
}
if_stmt_cnt=function(S, N)
{
if (S <= 2*N)
return(0)
total=0
for (k in 1:N)
{
P=Narayana(N, k)
if (S-P*k >= 2*N)
total=total+P*choose(S-P*k, 2*N)
}
return(total)
}
isc=matrix(nrow=25, ncol=5)
for (S in 5:20)
for (N in 1:5)
isc[S, N]=if_stmt_cnt(S, N)
print(isc) |
Recent Comments