The Shape of Code

Empirical data on requirements for commercial software systems is extremely hard to find. Massimo Felici’s PhD thesis on requirements evolution contains some very interesting data relating to an avionics system, but in many cases the graphs are plotted without numbers next to the axis tick marks. I imagine these numbers were removed because of concerns about what people who had been promoted beyond their level of competence might say (I would also have removed them if asked by the company who had provided the raw data, its a data providers market).

As soon as I saw the plot below I knew I could reverse engineer the original numbers for the plot in the top left.

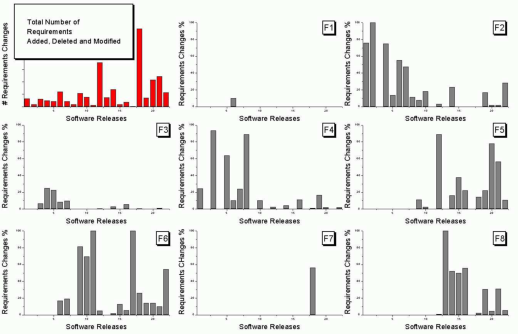
The top left plot is a total count of requirements added/deleted/modified in each of the 22 releases of the product. The eight other plots contain individual percentage information for each of the eight requirements features included in the total count product.

The key is that requirement counts have integer values and the percentages in the F1-8 plots are ratios that restrict the requirement counts to being exactly divisible by a calculated value.

I used WebPlotDigitizer, the goto tool for visually extracting data from plots, to obtain values for the height of each bar (for the time being assuming the unnumbered tick marks linearly increased in units of one).

Looking at the percentages for release one we see that 75% involved requirement feature F2 and 25% F4. This means that the total added/deleted/modified requirement count for release one must be divisible by 4. The percentages for release five are 64, 14 and 22; within a reasonable level of fuzziness this ratio is 9/2/3 and so the total count is probably divisible by 15. Repeating the process for release ten we get the ratio 7/4/1/28, probably divisible by 40; release six is probably divisible by 20, release nine by 10, release fourteen by 50 and fifteen by 10.

How do the release values extracted from the top left shape up when these divisibility requirements are enforced? A minimum value for the tick mark increment of 100 matches the divisibility requirements very well. Of course an increment of any multiple of 100 would match equally well, but until I spot a relationship that requires a larger value I will stick with 100.

I was not expecting to be so lucky in being able to extract useful ratios and briefly tried to be overly clever. Diophantine equations is the study of polynomial equations having integer solutions and there are lots of tools available for solving these equations. The data I have is fuzzy because it was extracted visually. A search for fuzzy diophantine equations locates some papers on how to solve such equations, but no obvious tools (there is code for solving fuzzy linear systems, but this technique does not restrict the solution space to integers).

The nearest possible solution path I could find involving statistics was: Statistical Analysis of Fuzzy Data.

If a reader has any suggestions for how to solve this problem automatically, given the percentage values, please let me know. Images+csvs for your delectation.