Archive
Optimizing floating-point expressions for accuracy
Floating-point arithmetic is one topic that most compiler writers tend to avoid as much as possible. The majority of programs don’t use floating-point (i.e., low customer demand), much of the analysis depends on the range of values being operated on (i.e., information not usually available to the compiler) and a lot of developers don’t understand numerical methods (i.e., keep the compiler out of the blame firing line by generating code that looks like what appears in the source).
There is a scientific and engineering community whose software contains lots of floating-point arithmetic, the so called number-crunchers. While this community is relatively small, many of the problems it works on attract lots of funding and some of this money filters down to compiler development. However, the fancy optimizations that appear in these Fortran compilers (until the second edition of the C standard in 1999 Fortran did a much better job of handling the minutia of floating-point arithmetic) are mostly about figuring out how to distribute the execution of loops over multiple functional units (i.e., concurrent execution).
The elephant in the floating-point evaluation room is result accuracy. Compiler writers know they have to be careful not to throw away accuracy (e.g., optimizing out what appear to be redundant operations in the Kahan summation algorithm), but until recently nobody had any idea how to go about improving the accuracy of what had been written. In retrospect one accuracy improvement algorithm is obvious, try lots of possible combinations of the ways in which an expression can be written and pick the most accurate.
There are lots of ways in which the operands in an expression can be paired together to be operated on; some of the ways of pairing the operands in a+b+c+d include (a+b)+(c+d), a+(b+(c+d)) and (d+a)+(b+c) (unless the source explicitly includes parenthesis compilers for C, C++, Fortran and many other languages (not Java which is strictly left to right) are permitted to choose the pairing and order of evaluation). For n operands (assuming the operators have the same precedence and are commutative) the number is combinations is 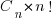 where
where 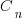 is the n’th Catalan number. For 5 operands there are 1680 combinations of which 120 are unique and for 10 operands
is the n’th Catalan number. For 5 operands there are 1680 combinations of which 120 are unique and for 10 operands 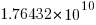 of which
of which 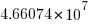 are unique.
are unique.
A recent study by Langlois, Martel and Thévenoux analysed the accuracy achieved by all unique permutations of ten operands on four different data sets. People within the same umbrella project are now working on integrating this kind of analysis into a compiler. This work is another example of the growing trend in compiler research of using the processing power provided by multiple cores to use algorithms that were previously unrealistic.
Over the last six years or so there has been lot of very interesting floating-point work going on in France, with gcc and llvm making use of the MPFR library (multiple-precision floating-point) for quite a while. Something very new and interesting is RangeLab which, given the lower/upper bounds of each input variable to a program (a simple C-like language) computes the range of the outputs as well as ranges for the roundoff errors (the tool assumes IEEE floating-point arithmetic). I now know that over the range [800, 1000] the expression x*(x+1) is a lot more accurate than x*x+x.
Update: See comment from @Eric and my response below.
Software memory management
I recently wrote about how computer memory capacity limits were a serious constraint for compiler writers. One technique used to increase the amount of memory available to a compiler (back in the days when pointers usually contained 16-bits) is software based paged memory management. Yes, compiler writers were generally willing to take the runtime performance hit to increase effectively accessible memory by around a factor of 10-25 (e.g., a 2 byte number used as an index into an array of 20 to 50 byte records).
The code to iterate over a data structure stored under the control of a software memory manager looks like the following (taken from a C to Pascal translator):
Var Flds : Sw_Ptr; (* in practice an integer *) T_Node : Sw_Node; (* in practice a pointer to a record *) Begin While Flds <> Sw_Nil Do (* Sw_Nil is the memory managers Nil value *) Begin Sw_Node_Ref(Cpswfile, Flds, T_Node, Mm_Readonly); If T_Node.Pn^.Node_Is<>N_Is_Field Then Verify_Error(Ve_Cputils, Ve_Scan_Fld); Scan(T_Node.Pn^.Field_Node.Ftype); Flds := T_Node.Pn^.Field_Node.Next; End; End; |
Where Sw_Node_Ref is a procedure in the memory management package that ensures the record denoted by Flds (whose value was obtained by a previous called to Sw_New_Node) is available in memory and returned in T_Node. Had Mm_ReadWrite rather than Mm_Readonly been specified the memory manager would assume that the record had been modified and when the page containing the record was swapped out of main memory it would write the contents of the page containing it to the swapfile (specified by the first argument, Cpswfile).
A call to Sw_Node_Ref only guarantees that the record is at the returned location until the next memory management procedure is called. This takes advantage of common usage which is: read a record, do something with its contents and then move on to the next one. The procedure Sw_Node_Ptr is available for when a record needs to be held in main memory across multiple Sw_ calls; this procedure locks a record in the limited capacity memory pool until explicitly freed (a Pascal style Mark/Release system was also available).
Multiple records were overlayed on a page (invariably 512 bytes) of storage. Some implementations used a fancy tool to create the overlay while others did it manually. The size of the pool in main memory used to hold swapped-in pages was specified when the memory manager was initialized; the maximum number of records that could be created by a call to Sw_New_Node was only limited by the maximum value of an integer and available disk space.
I learned about this implementation technique while on secondment at Intermetrics in the early 1980s, and they told me it came from the PQCC project of the mid 1970s. There is a paper in the Proceedings of the 1982 SIGPLAN symposium describing the system/library used by Intermetrics, which rambles on about nothing in particular and fails to say anything about software memory management (it is too useful an idea for a commercial company to tell anybody else); I don’t know of any other published description. Everybody I know who left Intermetrics to work on other compilers created their own implementation of a software memory management package.
Compiling to reduce the impact of soft errors on program output
Optimizing compilers have traditionally made code faster and smaller (sometimes a choice has to be made between faster/larger and slower/smaller). The huge growth in the use of battery power devices has created a new attribute for writers of optimizers to target, finding code sequences that minimise power consumption (I previously listed this as a major growth area in the next decade). Radiation (e.g., from cosmic rays) can cause a memory or processor bit to flip, known as a soft error, and I have recently been reading about how code can be optimized to reduce the probability that soft errors will alter the external behavior of a running program.
The soft error rate is usually quoted in FITs (Failure in Time), with 1 FIT corresponding to 1 error per 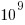 hours per megabit, or
hours per megabit, or 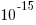 errors per bit-hour. A PC with 4 GB of DRAM (say 1000 FIT/Mb which increases with altitude and is 10 times greater in Denver, Colorado) has a MTBF (mean time between failure) of
errors per bit-hour. A PC with 4 GB of DRAM (say 1000 FIT/Mb which increases with altitude and is 10 times greater in Denver, Colorado) has a MTBF (mean time between failure) of 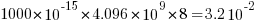 hours, around once every 33 hours. Calculating the FIT for processors is complicated.
hours, around once every 33 hours. Calculating the FIT for processors is complicated.
Uncorrected soft errors place a limit on the maximum number of computing nodes that can be usefully used by one application. At around 50,000 nodes, a system will be spending half its time saving checkpoints and restarting from previous checkpoints after an error occurs.
Why not rely on error correcting memory? Super computers containing terabytes are built containing error correcting memory, but this does not make the problem go away, it ‘only’ reduces it by around two orders of magnitude. Builders of commodity processors don’t use much error correction circuitry because it would increase costs/power consumption/etc for an increased level of reliability that the commodity market is not interested in; vendors of high-end processors add significant amounts of error correction circuitry.
Most of the compiler research I am aware of involves soft errors occurring on the processor, and this topic is discussed below; there has been some work on assigning variables deemed to be critical to a subset of memory that is protected with error correcting hardware. Pointers to other compiler research involving memory soft errors welcome.
A commonly used technique for handling hardware faults is redundancy, usually redundant hardware (e.g., three processors performing the same calculating and a majority vote used to decide which of the outputs to accept). Software only approaches include the compiler generating two or more independent machine code sequences for each source code sequence whose computed values are compared at various check points and running multiple copies of a program in different threads and comparing outputs. The
Shoestring compiler (based on llvm) takes a lightweight approach to redundancy by not duplicating those code sequences that are less affected by register bit flips (e.g., the value obtained from a bitwise AND that extracts 8 bits from a 32-bit register is 75% less likely to deliver an incorrect result than an operation that depends on all 32 bits).
The reliability of single ‘thread’ generated code can be improved by optimizing register lifetimes for this purpose. A value is loaded into a register and sometime later it is used one or more times. A soft error corrupting register contents after the last use of the value it contains has no impact on program execution, the soft error has to occur between the load and last use of the value for it to possibly influence program output. One group of researchers modified a compiler (Trimaran) to order register usage such that the average interval between load and last usage was reduced by 10%, compared to the default behavior.
Developers don’t have to wait for compiler or hardware support, they can improve reliability by using algorithms that are robust in the presence of ‘faulty’ hardware. For instance, the traditional algorithms for two-process mutual exclusion are not fault-tolerant; a fault-tolerant mutual exclusion algorithm using 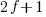 variables, where a single fault may occur in up to
variables, where a single fault may occur in up to  variables is available.
variables is available.
What I know of Dennis Ritchie’s involvement with C
News that Dennis Ritchie died last weekend surfaced today. This private man was involved in many ground breaking developments; I know something about one of the languages he designed, C, so I will write about that. Ritchie has written about the development of C language.
Like many language designers the book he wrote “The C Programming Language” (coauthored with Brian Kernighan in 1978) was the definitive reference for users; universally known as K&R. The rapid growth in C’s popularity led to lots of compilers being written, exposing the multiple ways it was possible to interpret some of the wording in K&R.
In 1983 ANSI set up a committee, X3J11, to create a standard for C. With one exception Ritchie was happy to keep out of the fray of standardization; on only one occasion did he feel strongly enough to step in and express an opinion and the noalias keyword disappeared from the draft (the restrict keyword surfaced in C99 as a different kind of beast).
A major contribution to the success of the C Standard was the publication of an “ANSI Standard” version of K&R (there was a red “ANSI C” stamp on the front cover and the text made use of updated constructs like function prototypes and enumeration types), its second edition in 1988. Fans of the C Standard could, and did, claim that K&R C and ANSI C were the same language (anybody using the original K&R was clearly not keeping up with the times).
Ritchie publicly admitted to making one mistake in the design of C. He thinks that the precedence of the & and | binary operators should have been greater than the == operator. I can see his point, but an experiment I ran a few years ago suggested it is amount of experience using a set of operator precedence rules that is the primary contributor to developer knowledge of the subject.
Some language designers stick with their language, enhancing it over the years (e.g., Stroustrup with C++), while others move on to other languages (e.g., Wirth with Pascal, Modula-2 and Oberon). Ritchie had plenty of other interesting projects to spend his time on and took neither approach. As far as I can tell he made little or no direct contribution to C99. As head of the research department that created Plan 9 he must have had some input to the non-Standard features of their C compiler (e.g., no support for #if and support for unnamed structures).
While the modern C world may not be affected by his passing, his ability to find simple solutions to complicated problems will be a loss to the projects he was currently working on.
Memory capacity and commercial compiler development
When I started out in the compiler business in the 80s many commercial compilers were originally written by one person. A very good person who dedicated himself (I have never heard of a woman doing this) to the job (i.e., minimal social life) could produce a commercially viable product for a non-huge language (e.g., Fortran, Pascal, C, etc and not C++, Ada, etc) in 12-18 months. Companies who decide to develop a compiler in-house tend to use a team of people and take longer because that is how they work, and they don’t want to depend on one person and anyway such a person might not be available to them.
Commercially viable compiler development stayed within the realm of an individual effort until sometime in the early 90s. What put the single individual out of business was the growth in computer memory capacity into the hundreds of megabytes and beyond. Compilers have to be able to run within the limits of developer machines; you won’t sell many compilers that require 100M of memory if most of your customers don’t have machines with 100M+ of memory.
Code optimizers eat memory and this prevented many optimizations that had been known about for years appearing in commercial products. Once the machines used for software development commonly contained 100M+ of memory compiler vendors could start to incorporate these optimizations into their products.
Improvements in processor speed also helped. But developers are usually willing to let the compiler take a long time to optimize the code going into a final build, provided development compiles run at a reasonable speed.
The increase in memory capacity created the opportunity for compilers to improve and when some did improve they made it harder for others to compete. Suddenly an individual had to spend that 12-18 months, plus many more months implementing fancy optimizations; developing a commercially viable compiler outgrew the realm of individual effort.
Some people claim that the open source model was the primary driver in killing off commercial C compiler development. I disagree. My experience of licensing compiler source was that companies preferred a commercial model they were familiar with and reacted strongly against the idea of having to make available any changes they made to the code of an open source program. GCC (and recently llvm) succeeded because many talented people contributed fancy optimizations and these could be incorporated because developer machines contained lots of memory. If storage had not dramatically increased gcc would probably not be the market leader it is today.
Automatically improving code
Compared to 20 or 30 years ago we know a lot more about the properties of algorithms and better ways of doing things often exist (e.g., more accurate, faster, more reliable, etc). The problem with this knowledge is that it takes the form of lots and lots of small specific details, not the kind of thing that developers are likely to be interested in, or good at, remembering. Rather than involve developers in the decision-making process, perhaps the compiler could figure out when to substitute something better for what had actually been written.
While developers are likely to be very happy to see what they have written behaving as accurately and reliably as they had expected (ignorance is bliss), there is always the possibility that the ‘less better’ behavior of what they had actually written had really been intended. The following examples illustrate two relatively low level ‘improvement’ transformations:
- this case is probably a long-standing fault in many binary search and merge sort functions; the relevant block of developer written code goes something like the following:
while (low <= high) { int mid = (low + high) / 2; int midVal = data[mid]; if (midVal < key) low = mid + 1 else if (midVal > key) high = mid - 1; else return mid; }
The fault is in the expression
(low + high) / 2which overflows to a negative value, and returns a negative value, if the number of items being sorted is large enough. Alternatives that don’t overflow, and that a compiler might transform the code to, include:low + ((high - low) / 2)and(low + high) >>> 1. - the second involves summing a sequence of floating-point numbers. The typical implementation is a simple loop such as the following:
sum=0.0; for i=1 to array_len sum += array_of_double[i];
which for large arrays can result in
sumlosing a great deal of accuracy. The Kahan summation algorithm tries to take account of accuracy lost in one iteration of the loop by compensating on the next iteration. If floating-point numbers were represented to infinite precision the following loop could be simplified to the one above:sum=0.0; c=0.0; for i = 1 to array_len { y = array_of_double[i] - c; // try to adjust for previous lost accuracy t = sum + y; c = (t - sum) - y; // try and gets some information on lost accuracy sum = t; }
In this case the additional accuracy is bought at the price of a decrease in performance.
Compiler maintainers are just like other workers in that they want to carry on working at what they are doing. This means they need to keep finding ways of improving their product, or at least improving it from the point of view of those willing to pay for their services.
Many low level transformations such as the above two examples would be not be that hard to implement, and some developers would regard them as useful. In some cases the behavior of the code as written would be required, and its transformed behavior would be surprising to the author, while in other cases the transformed behavior is what the developer would prefer if they were aware of it. Doesn’t it make sense to perform the transformations in those cases where the as-written behavior is least likely to be wanted?
Compilers already do things that are surprising to developers (often because the developer does not fully understand the language, many of which continue to grow in complexity). Creating the potential for more surprises is not that big a deal in the overall scheme of things.
sparse can now generate executables
How can you be confident that a source code analysis tool is correct when its analysis of a file does not result in any warning being generated? The best way I know of addressing this issue is for the analysis tool to be capable of generating an executable from the source. Executing a moderately large program requires that the translator get all sorts of complicated analysis correct and provides a huge boost to confidence of correctness compared to an analysis tool that does not have this ability.
Congratulations to the maintainers of sparse (a Linux kernel specific analysis tool started by Linus Torvalds in 2003) for becoming one of the very small number of source code analysis tools capable of generating executable programs.
The Model C Implementation is another tool capable of generating executables. I would love to be able to say that the reason for this was dedication to perfection by the project team, however, the truth is that it started life as a compiler and became an analyzer later.
Clang, the C front end+analyzer to llvm is often referred to as a static analyzer. While it does perform some static checking (like gcc does when the -Wall option is specified) a lot more checks needs to be supported before it can be considered on a par with modern static analysis tools.
GCC’s Treehydra project works via a plug-in to the compiler. This project has yet to live up to its potential, so we can delay discussion of whether it should be classified as a standalone system or an executable generator.
I cannot think of any other ‘full language’ static analysis tools capable of generating executable programs (the C-semantics tool restricts its checks to those required by the C Standard, and I think tools need to do a lot more than this to be considered static analysis tools). Corrections to my lack of knowledge welcome.
I was a little concerned that there were plans afoot to migrate sparse to becoming the build compiler for the Linux kernel. Linus answered my query by saying that this was never a goal.
Estimating the reliability of compiler subcomponent
Compiler stress testing can be used for more than finding bugs in compilers, it can also be used to obtain information about the reliability of individual components of a compiler. A recent blog post by John Regehr, lead investigator for the Csmith project, covered a proposal to improve an often overlooked aspect of automated compiler stress testing (removing non-essential code from a failing test case so it is small enough to be acceptable in a bug report; attaching 500 lines of source to a report in a sure fire way for it to be ignored) triggered this post. I hope that John’s proposal is funded and it would be great if the researchers involved also received funding to investigate component reliability using the data they obtain.
One process for estimating the reliability of the components of a compiler, or any other program, is:
- divide the compiler into a set of subcomponents. These components might be a collection of source files obtained through cluster analysis of the source, obtained from a functional analysis of the implementation documents or some other means,
- count the number of times each component executes correctly and incorrectly (this requires associating bugs with components by tracing bug fixes to the changes they induce in source files; obtaining this information will consume the largest amount of the human powered work) while processing lots of source. The ratio of these two numbers, for a given component, is an estimate of the reliability of that component.
How important is one component to the overall reliability of the whole compiler? This question can be answered if the set of components is treated as a Markov chain and the component transition probabilities are obtained using runtime profiling (see Large Empirical Case Study of Architecture–based Software Reliability by Goševa-Popstojanova, Hamill and Perugupalli for a detailed discussion).
Reliability is a important factor in developers’ willingness to enable some optimizations. Information from a component reliability analysis could be used to support an option that only enabled optimization components having a reliability greater than a developer supplied value.
The one big threat to validity of this approach is that stress tests are not representative of typical code. One possibility is to profile the compiler processing lots of source (say of the order of a common Linux distribution) and merge the transition probabilities, probably weighted, to those obtained from stress tests.
Compiler benchmarking for the 21st century
I would like to propose a new way of measuring the quality of a compiler’s code generator: The highest quality compiler is one that generates identical code for all programs that produce the same output, e.g., a compiler might spot programs that calculate pi and always generate code that uses the most rapidly converging method known. This is a very different approach to the traditional methods based on using (mostly) execution time or size (usually code but sometimes data) as a measure of quality.
Why is a new measurement method needed, and why choose this one? It is relatively easy for compiler vendors to tune their products to the commonly used benchmark and they seem to have lost their role as drivers for new optimization techniques. Different developers have different writing habits and companies should not have to waste time and money changing developer habits just to get the best quality code out of a compiler; compilers should handle differences in developer coding habits and not let it affect the quality of generated code. There are major savings to be had by optimizing the effect that developers are trying to achieve rather than what they have actually written (these days new optimizations targeting at what developers have written show very low percentage improvements).
Deducing that a function calculates pi requires a level of sophistication in whole program analysis that is unlikely to be available in production compilers for some years to come (ok, detecting 4*atan(1.0) is possible today). What is needed is a collection of compilable files containing source code that aims to achieve an outcome in lots of different ways. To get the ball rolling the “3n times 2” problem is presented as the first of this new breed of benchmarks.
The “3n times 2” problem is a variant on the 3n+1 problem that has been tweaked to create more optimization opportunities. One implementation of the “3n times 2” problem is:
if (is_odd(n)) n = 3*n+1; else n = 2*n; // this is n = n / 2; in the 3n+1 problem |
There are lots of ways of writing code that has the same effect, some of the statements I have seen for calculating n=3*n+1 include: n = n + n + n + 1, n = (n << 1) + n + 1 and n *= 3; n++, while some of the ways of checking if n is odd include: n & 1, (n / 2)*2 != n and n % 2.
I have created a list of different ways in which 3*n+1 might be calculated and is_odd(n) might be tested and written a script to generate a function containing all possible permutations (to reduce the number of combinations no variants were created for the least interesting case of n=2*n, which was always generated in this form). The following is a snippet of the generated code (download everything):
if (n & 1) n=(n << 2) - n +1; else n*=2; if (n & 1) n=3*n+1; else n*=2; if (n & 1) n += 2*n +1; else n*=2; if ((n / 2)*2 != n) { t=(n << 1); n=t+n+1; } else n*=2; if ((n / 2)*2 != n) { n*=3; n++; } else n*=2; |
Benchmarks need a means of summarizing the results and here I make a stab at doing that for gcc 4.6.1 and llvm 2.9, when executed using the -O3 option (output here and here). Both compilers generated a total of four different sequences for the 27 'different' statements (I'm not sure what to do about the inline function tests and have ignored them here) with none of the sequences being shared between compilers. The following lists the number of occurrences of each sequence, e.g., gcc generated one sequence 16 times, another 8 times and so on:
gcc 16 8 2 1 llvm 12 6 6 3
How might we turn these counts into a single number that enables compiler performance to be compared? One possibility is to award 1 point for each of the most common sequence, 1/2 point for each of the second most common, 1/4 for the third and so on. Using this scheme, gcc gets 20.625, and llvm gets 16.875. So gcc has greater consistency (I am loathed to use the much overused phrase higher quality).
Now for a closer look at the code generated.
Both compilers always generated code to test the least significant bit for the conditional expressions n & 1 and n % 2. For the test (n / 2)*2 != n gcc generated the not very clever right-shift/left-shift/compare while llvm and'ed out the bottom bit and then compared; so both compilers failed to handle what is a surprisingly common check for a number being odd.
The optimal code for n=3*n+1 on a modern x86 processor is (lots of register combinations are possible, let's assume rdx contains n) leal 1(%rdx,%rdx,2), %edx and this is what both compilers generated a lot of the time. This locally optimal code is not always generated because:
- gcc fails to detect that
(n << 2)-n+1is equivalent to(n << 1)+n+1and generates the sequenceleal 0(,%rax,4), %edx ; subl %eax, %edx ; addl $1, %edx(I pointed this out to a gcc maintainer sometime ago, and he suggested reporting it as a bug). This 'bug' occurs three times in total. - For some forms of the calculation llvm generates globally better code by taking the else arm into consideration. For instance, when the calculation is written as
n += (n << 1) +1llvm deduces that(n << 1)and the2*nin theelseare equivalent, evaluates this value into a register before performing the conditional test thus removing the need for an unconditional jump around the 'else' code:leal (%rax,%rax), %ecx testb $1, %al je .LBB0_8 # BB#7: orl $1, %ecx # deduced ecx is even, arithmetic unit not needed! addl %eax, %ecx .LBB0_8:
This more efficient sequence occurs nine times in total.
The most optimal sequence was generated by gcc:
testb $1, %dl leal (%rdx,%rdx), %eax je .L6 leal 1(%rdx,%rdx,2), %eax .L6: |
with llvm and pre 4.6 versions of gcc generating the more traditional form (above, gcc 4.6.1 assumes that the 'then' arm is the most likely to be executed and trades off a leal against a very slow jmp):
testb $1, %al je .LBB0_5 # BB#4: leal 1(%rax,%rax,2), %eax jmp .LBB0_6 .LBB0_5: addl %eax, %eax .LBB0_6: |
There is still room for improvement, perhaps by using the conditional move instruction (which gcc actually generates within the not-very-clever code sequence for (n / 2)*2 != n) or by using the fact that eax already holds 2*n (the potential saving would come through a reduction in complexity of the internal resources needed to execute the instruction).
llvm insists on storing the calculated value back into n at the end of every statement. I'm not sure if this is a bug or a feature designed to make runtime debugging easier (if so it ought to be switched off by default).
Missed optimization opportunities (not intended to be part of this benchmark and if encountered would require a restructuring of the test source) include noticing that if  is odd then
is odd then 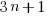 is always even, creating the opportunity to perform the following multiply by 2 without an if test.
is always even, creating the opportunity to perform the following multiply by 2 without an if test.
Perhaps one day, compilers will figure out when a program is calculating pi and generate code that uses the best known algorithm. In the meantime, I am interested in hearing suggestions for additional different-algorithm-same-code benchmarks.
Fibonacci and JIT compilers
To maximize a compiler’s ability to generate high quality code many programming language standards do not specify the order in which the operands of a binary operator are evaluated. Most of the time the order of operand evaluation does not matter because all orders produce same final result. For instance in x + y the value of x may be obtained followed by obtaining the value of y and the two values added, alternatively the value of y may be obtained first followed by obtaining the value of x and the two values added; optimizers make use of local context information (e.g., holding one of the values in a register so it is immediately available for use in the evaluation of multiple instances of x) to work out which order produces the highest quality code.
If one of the operands is a function call that modifies the value of the other operand the result may depend on the order of evaluation. For instance, in:
int x; int set_x(void) { x=1; return 1; } int two_values(void) { x=0; return x + set_x(); } |
a left to right evaluation order of the return expression in two_values produces the value 1, while a right to left evaluation order produces the value 2. Every now and again developers accidentally write code that does something like this and are surprised to see program behavior change when they use different compiler options, a new version of the compiler or a different compiler (all things that can result in the order of evaluation changing for a given expression).
It is generally assumed that two calls to two_values within the same program will always produce the same answer, i.e., the decision on which order of evaluation to use is made at compile time and never changes while a program is running. Neither the C++ or C Standard requires that the evaluation order be fixed prior to program execution and use of a just-in-time compiler could result in the value returned by two_values alternating between 1 and 2. Some languages (e.g., Java) for which JIT compilers are expected to be used specify the exact order in which operands have to be evaluated.
One possible way of finding out whether a JIT compiler is being used for your C/C++ program is to test the values returned by two calls to two_values. A JIT compiler may, but is not required, to return different values on each call. Of course a decide-prior-to-execution C/C++ compiler does have the option of optimizing the following function to return true or false on the basis that the standard permits this behavior, but I would be very surprised to see this occur in practice:
bool Schrödinger(void) { return two_values() == two_values(); } |
The runtime variability offered by JIT compilers makes it possible to write a program whose output can be any value between 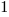 and
and 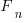 (the
(the  ‘th Fibonacci number, where
‘th Fibonacci number, where n is read from the input):
#include <stdio.h> int x; int set_x(int ret_val) { x=1; return ret_val; } int two_unspec(void) { x=0; return x + set_x(1); } int add_zero(val) { x=0; return val - x + set_x(0); } int fib(int fib_num) { if (fib_num > 3) return fib(fib_num-2) + add_zero(fib(fib_num-1)); else if (fib_num == 3) return two_unspec(); else return 1; } int main(void) { int n; scanf("%d", &n); printf("Fibonacci %d = %d\n", n, filb(n)); } |
The C-semantics tool will ‘execute’ this program and produce a list of the 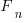 possible outputs (a PhD project under active development; the upper limit is currently around the 6th Fibonacci number which requires 11 hours and produces a 50G log file).
possible outputs (a PhD project under active development; the upper limit is currently around the 6th Fibonacci number which requires 11 hours and produces a 50G log file).
A decide-prior-to-execution compiler has a maximum choice of four possible outputs for a given input value and for a given executable the output produced by different input values will be perfectly correlated.
Recent Comments