Archive
How to avoid being a victim of Brooks’ law
The oft cited book The Mythical Man Month contains a statement that has become known as Brooks’ Law: “Adding manpower to a late software project makes it later”.
When people join a project they need to learn project specific information, this is information that can only be obtained from people already working on the project. Training up new staff (e.g., developers, documentation writers) reduces the amount of effort being directly invested in building the system; it is an investment in people whose benefit is the post-training productivity of those people adding their effort to the project.
Let’s assume that a newbie diverts from the project they are joining an amount of effort units of time, 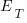 , in training without contributing anything, and that this training/investment lasts for
, in training without contributing anything, and that this training/investment lasts for 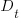 units of time after which the trained person contributes an average of
units of time after which the trained person contributes an average of 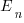 of effort per unit of time until the project deadline. This investment in a newbie will cause the project to be delayed unless the following inequality holds:
of effort per unit of time until the project deadline. This investment in a newbie will cause the project to be delayed unless the following inequality holds:
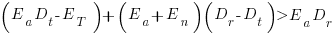

where 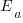 is the average daily project effort available before a newbie joins and
is the average daily project effort available before a newbie joins and 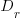 is the number of units of time between the start of training and the delivery date/time.
is the number of units of time between the start of training and the delivery date/time.
This simplifies to:
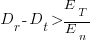

an equation that makes the obvious point that as the deadline approaches the amount of time and effort spent training newbies needs to decrease if a worthwhile payback is to be achieved in the available time.
The quantity 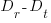 is the amount of time remaining after the newbie finishes training (in practice this is rarely a well defined point in time, but let’s keep things simple) and is the only easily obtained information in the equation.
is the amount of time remaining after the newbie finishes training (in practice this is rarely a well defined point in time, but let’s keep things simple) and is the only easily obtained information in the equation.
The effort contribution of the newbie, 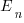 , could be approximated using information on the effort contribution of other people doing a similar job on the project. At least it could be if data was available on what their effort contribution was, and we overlooked the possible 5:1 difference in performance found between software developers. In practice a newbie’s effort contribution ramps up from zero, perhaps even starting during the training period, to a relatively constant long term daily average. How long does it take for
, could be approximated using information on the effort contribution of other people doing a similar job on the project. At least it could be if data was available on what their effort contribution was, and we overlooked the possible 5:1 difference in performance found between software developers. In practice a newbie’s effort contribution ramps up from zero, perhaps even starting during the training period, to a relatively constant long term daily average. How long does it take for 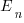 to reach the long term average? I have no idea.
to reach the long term average? I have no idea.
How much effort, 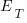 , goes into training a newbie? A very important factor will obviously be their existing level of expertise with the application domain, tools being used, coding skills, etc (pretty much everything was new, back in the day, for the project analysed by Brooks, so
, goes into training a newbie? A very important factor will obviously be their existing level of expertise with the application domain, tools being used, coding skills, etc (pretty much everything was new, back in the day, for the project analysed by Brooks, so 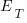 was probably very high). There is also the somewhat nebulous but very important ability, or lack of, to pick things up quickly.
was probably very high). There is also the somewhat nebulous but very important ability, or lack of, to pick things up quickly.
Could data on 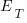 be obtained by recording every encounter the newbie has with existing project members? This would certainly enable information on first order time interactions to be obtained, but it would not tell us anything about the knock on effects caused by the work of an existing project member being delayed because they were investing in the newbie.
be obtained by recording every encounter the newbie has with existing project members? This would certainly enable information on first order time interactions to be obtained, but it would not tell us anything about the knock on effects caused by the work of an existing project member being delayed because they were investing in the newbie.
If many people are being added to a project at the same time it is easy to imagine it grinding to a halt because of all the minor congestion that occurs within the network of dependencies that project progress is waiting on.
I have not been able to locate any applicable data relating to training on software development projects, but then this area is at the edge of what I know about. Pointers to data most welcome.
Recent Comments