Archive
Plotting artifacts when the axis involves lines of code
While reading a report from the very late Rome period, the plot below caught my attention (the regression line was not in the original plot). The points follow a general trend, suggesting that when implementing a module, lines of code written per man-hour increases as the size of the module increases (in LOC). There are explanations for such behavior: perhaps module implementation time is mostly think-time that is independent of LOC, or perhaps larger modules contain more lines that can be quickly implemented (code+data).
Then I realised that the pattern of points was generated by a mathematical artifact. Can you spot the artifact?
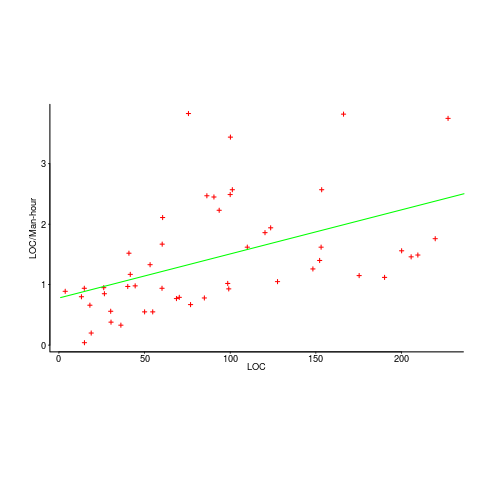
The x-axis shows LOC, and the y-axis shows LOC/man-hour. Just plotting LOC against LOC would produce a row of points along a straight line, and if we treat dividing by man-hours as roughly equivalent to dividing by a random number (which might have some correlation with LOC), the result is points scattered around a line going up to the right.
If LOC-per-hour were constant, the points would form a horizontal line across the plot.
In the below left plot, from a different report (whose axis are function-points, and function-points implemented per month), the author has fitted a line, and it is close to horizontal (suggesting that the mean FP-per-month is constant).
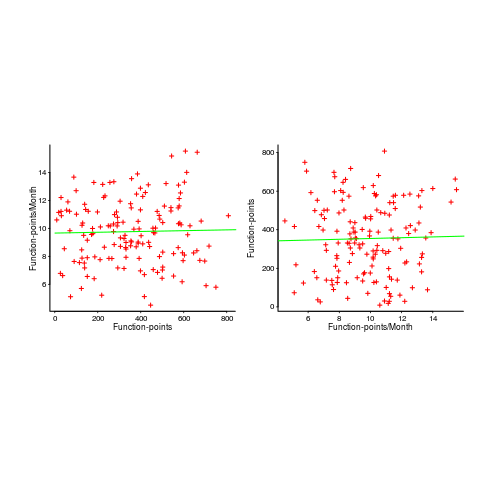
In fact the points are essentially random, and the line is a terrible fit (just how terrible is shown by switching the axis and refitting the line, above right; the refitted line should be vertical, but is horizontal. There is no connection between FP and FP-per-month, which is a good thing because the creators of function-points intended this to be true).
What process might generate this random scattering, rather than the trend seen in the first plot? If the implementation time was proportional to both the number of FP and some uniform random component, then the FP/time ratio would have the pattern seen.
The plots below show module size (in LOC) against man-hour (left) and FP against months (right):
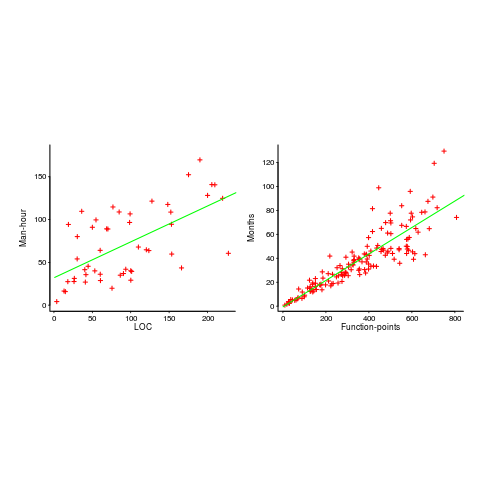
The module-LOC points are all over the place, while the FP points look as-if they are roughly consistent. Perhaps the module-LOC measurements came from a wide variety of sources, and we should not expect a visually pleasant trend.
Plotting LOC against LOC appears in other guises. Perhaps the most common being plotting fault-density against LOC; fault-density is generally calculated as faults/LOC.
Of course the artifacts also occur when plotting other kinds of measurements. Lines of code happens to be a commonly plotted quantity (at least in software engineering).
Histogram using log scale creates a visual artifact
The following plot appears in the paper Stack Overflow in Github: Any Snippets There?
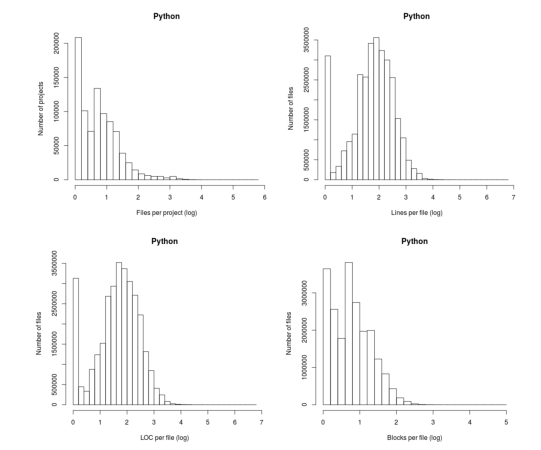
Don’t those twin peaks in the top-left/bottom-right plots reach out and grab your attention? I immediately thought of fitting a mixture of two Poisson distributions; No, No, No, something wrong here. The first question of data analysis is: Do I believe the data?
The possibility of fake data does not get asked until more likely possibilities have been examined first.
The y-axis is a count of things and the x-axis shows the things being counted; source files per project and functions per file, in this case.
All the measurements I know of show a decreasing trend for these things, e.g., lots of projects have a few files and a few projects have lots of files. Twin peaks is very unexpected.
I have serious problems believing this data, because it does not conform to my prior experience. What have the authors done wrong?
My first thought was that a measuring mistake had been made; for some reason values over a certain range were being incorrectly miscounted.
Then I saw the problem. The plot was of a histogram and the x-axis had a logarithmic scale. A logarithmic axis compresses the range in a non-linear fashion, which means that variable width bins have to be used for histograms and the y-axis represents density (not a count).
Taking logs and using the result to plot a histogram usually produces a curve having a distorted shape, not twin peaks. I think the twin peaks occur here because integer data are involved and the bin width just happened to have the ‘right’ value.
Looking at the plot below, the first bin contains values for x=1 (on an un-logged scale), the second bin for x=2, the third bin for x=3, but the fourth bin contains values for x=c(4, 5, 6). The nonlinear logarithmic compression, mapped to integers, means that the contents of three values are added to a single bin, creating a total that is larger than the third bin.
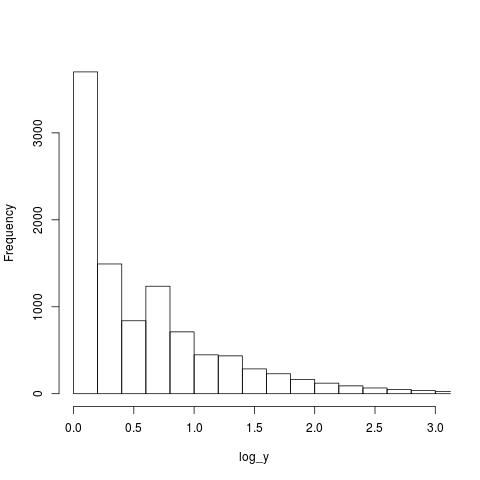
The R code that generated the above plot:
x=1:1e6 y=trunc(1e6/x^1.5) log_y=log10(y) hist(log_y, n=40, main="", xlim=c(0, 3)) |
I tried to mimic the pattern seen in the first histogram by trying various exponents of a power law (a common candidate for this kind of measurement), but couldn’t get anything to work.
Change the bin width can make the second peak disappear, or rather get smeared out. Still a useful pattern to look out for in the future.
Recent Comments